Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 5 Module 4 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 5 Module 4
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 4 Session 1 Answer Key
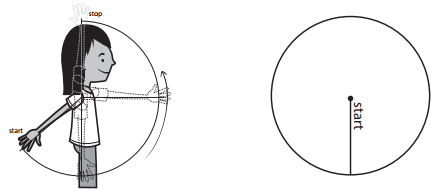
Measuring the Range of Motion of Your Joints
Work with a partner to test how much you can rotate each of the joints shown below. Each of you will sketch. First sketch the ending points of the joint’s rotation. Then use your pattern blocks to estimate the degree of rotation to the nearest 10 degrees. When testing your joints, only bend as far as is comfortable: don’t rotate your joints until it feels difficult or painful!
Question 1.
Knee
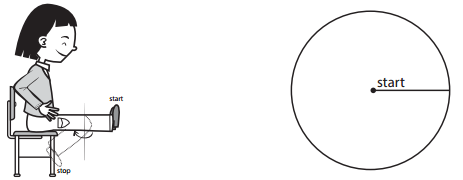
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 240°. The approximate fraction of a complete turn: \(\frac{2}{3}\).
Explanation:
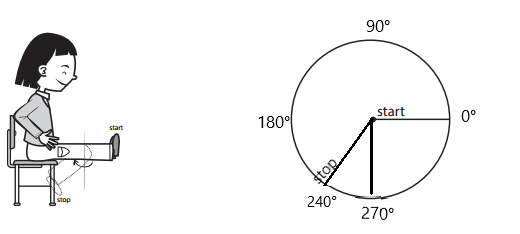
The approximate degree of rotation is 240°as she started from 0 and stopped at 240°.
The approximate fraction of a complete turn: \(\frac{240}{360}\) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
Question 2.
Shoulder: to the side
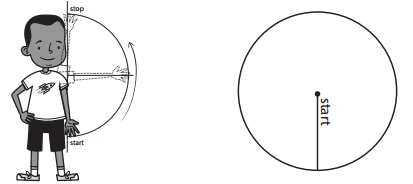
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 180°. The approximate fraction of a complete turn: \(\frac{1}{2}\).
Explanation:
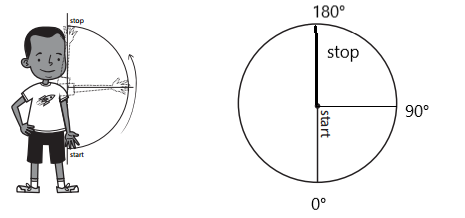
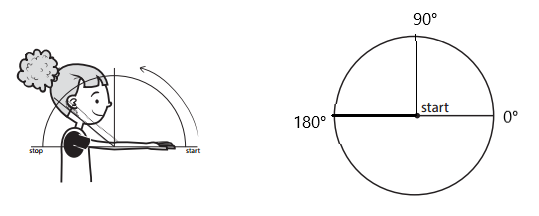
Question 3.
Elbow
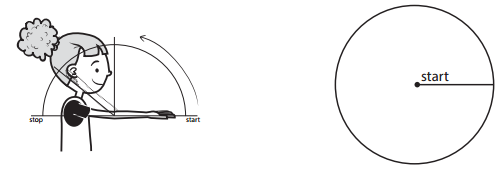
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 180°. The approximate fraction of a complete turn: \(\frac{1}{2}\).
Explanation:
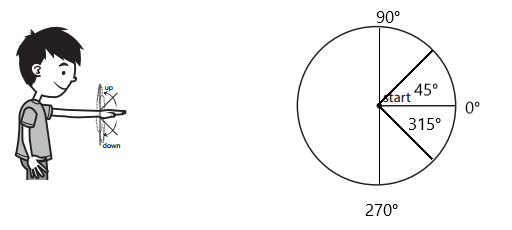
Question 4.
Wrist
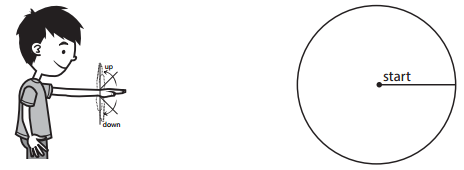
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 90°. The approximate fraction of a complete turn: \(\frac{1}{4}\).
Explanation:
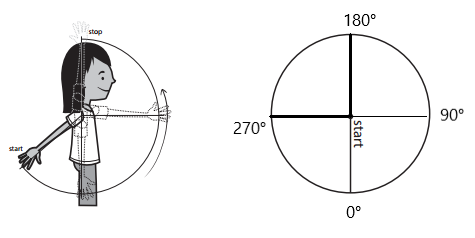
Question 5.
Shoulder: back and front
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 270°. The approximate fraction of a complete turn: \(\frac{3}{4}\).
Explanation:
Question 6.
Your choice
approximate degrees of rotation: ________________
approximate fraction of a complete turn: ________________
Answer:
The approximate degree of rotation is 270°. The approximate fraction of a complete turn: \(\frac{3}{4}\).
Explanation:
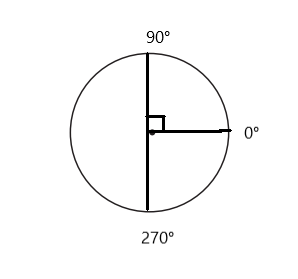
Drawing Angles of Rotation
Draw and label the angles that are equal to each fraction of a whole turn around the circle. Use your pattern blocks to make the angles exact. Remember that there are 360 degrees in a full turn around the circle.
ex: Draw and label \(\frac{1}{6}\) turn.
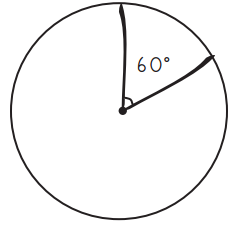
Question 1.
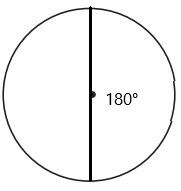
Draw and label \(\frac{1}{2}\) turn.
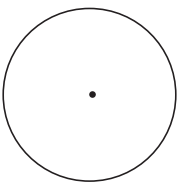
Answer:
Explanation:
Given,
latex]\frac{1}{2}[/latex] turn.
latex]\frac{1}{2}[/latex] × 360
180°.
Question 2.
Draw and label \(\frac{1}{4}\) turn.

Answer:
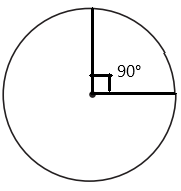
Explanation:
Given,
\(\frac{1}{4}\) turn.
\(\frac{1}{4}\) × 360
90°
Question 3.
Draw and label \(\frac{3}{4}\) turn.

Answer:
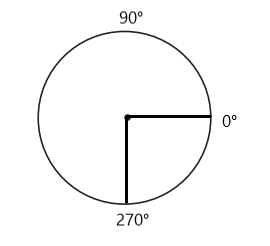
Explanation:
Given,
\(\frac{3}{4}\) turn.
1 turn = 360°
\(\frac{3}{4}\) × 360 = 270°
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 4 Session 2 Answer Key
Geometry Measurement Problems
Mr. White asked some of his fourth graders to demonstrate making turns in their square-shaped classroom. Each of the students started their turn facing either the front or the back of the classroom.
Question 1.
Mia started facing the front wall of the classroom. She turned 60° to the right. Then she turned 60° more to the right, and then 60° more.
a. How many degrees did Mia turn in all? Use numbers and a labeled sketch to solve this problem.
Answer:
Mia turned a total of 180° in all.
Explanation:
Given,
Mia started facing the front wall of the classroom
She turned 60° to the right.
Next, she turned 60° more to the right and 60° more.
60° + 60° + 60° = 180°
b. Which wall in the classroom was Mia facing when she stopped?
Answer:
No Mia faces the back side of the classroom.
Question 2.
Marcus started facing the back of the classroom. He turned 360°. Then he kept on turning in the same direction, 180° more.
a. How many degrees did Marcus turn in all? Use numbers and a labeled sketch to solve this problem. Show all your work.
Answer:
360° + 180° = 540°.
b. Which wall in the classroom was Marcus facing when he stopped?
Answer:
Marcus faces the back side of the wall in the classroom when he stopped.
Question 3.
Sara started facing the front of the classroom. She turned 45° to the left, and then kept on turning to the left—80° more, then 45° more, then 120° more. Did she turn all the way around in a complete circle, so she was facing the front of the room again? If not, how many more degrees would she need to turn to complete the circle? Use numbers and a labeled sketch to solve this problem. Show all your work.
Answer:
No, she did not turn all the way around in a complete circle. And she needed 70° more to turn to complete the circle.
Explanation:
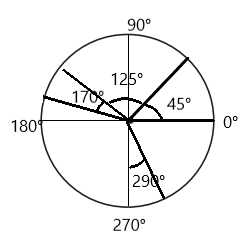
Sara turned 45° to the left
And kept on turning to the left 80° more, then 45° more, then 120° more.
Total degrees she turned are 45 + 80 + 45 + 120 = 290°
A full turn has 360°
360° – 290° = 70°
she needed 70° more to turn to complete the circle.
Question 4.
Anthony started by facing the back wall of the classroom. He turned 90° to the right, and then 90 more degrees to the right. After that, he kept turning to the right, 45° more, 45° more, and 45° more. Did he turn all the way around in a complete circle? If not, how many more degrees would he need to turn to complete the circle? Use numbers and a labeled sketch to solve this problem. Show all your work.
Answer:
No, she did not turn all the way around in a complete circle. And she needed 45° more to turn to complete the circle.
Explanation:
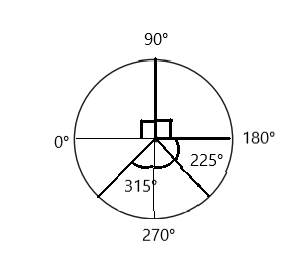
Given,
Anthony turned 90° right.
90 more degrees to the right.
the right, 45° more, 45° more, and 45° more.
Total degrees = 90 + 90 + 45 + 45 + 45
= 315°
she needed 360° -315° = 45° more to complete the circle.
Question 5.
Measure the two angles with your protractor. What is the difference between the measure of angle a and angle b?
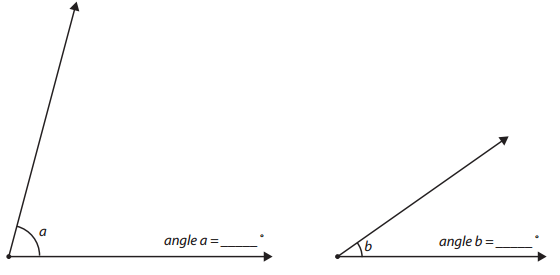
The difference between the measure of angle a and angle b is _____________ degrees.
Answer:
The difference between the measure of angle a and angle b is 55° degrees.
Explanation:
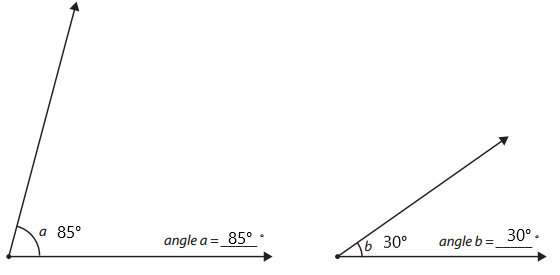
angle a = 85° and angle b is 30°
The difference between angle a and angle b is 85° – 30° = 55°
Question 6.
CHALLENGE If the area of a rectangle is 240 and one dimension is 40, what is the other dimension? Use numbers and a labeled sketch to solve this problem.
Answer:
The other dimension is 6.
Explanation:
Given,
The area of the rectangle is 240
The other dimension is 40
Area of the rectangle is l × b
240 = l × b
240 = 40 × b
b = 240 ÷ 40
b = 6
Hence the other dimension is 6.
Question 7.
CHALLENGE If the perimeter of a rectangle is 90 and one dimension is 20, what is the other dimension? Use numbers and a labeled sketch to solve this problem.
Answer:
The other dimension is 25.
Explanation:
Given,
The perimeter of a rectangle is 90
The other dimension is 20
We know the perimeter of the rectangle is 2(l+b)
2(l+b) = 90
2(20+b) = 90
40 + 2b = 90
2b = 90 – 40
2b = 50
b = 50 ÷ 2
b = 25
Therefore the other dimension is 25.
Question 8.
CHALLENGE Write two different combinations of six turns each so that the person who is turning ends up facing the same way he started.
Note: You don’t have to stick with a single turn of360° as long as the person who is turning ends up facing the same way he started.
Answer:
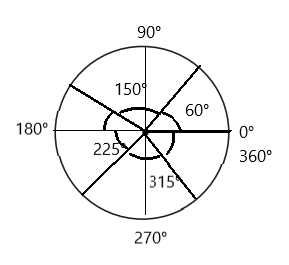
Explanation:
The person started turning facing the same at 0°
60° + 90° + 30° + 45° + 90° + 45° = 360°
Hence the person who is turning ended up facing the same way he started.
Turns & Fractions at the Skate Park
Question 1.
A group of kids were practicing tricks on their skateboards at the skate park. Solve the following problems about the kids and their skateboard tricks. Write and solve an equation for each problem.

a. Molly made a turn on her board that was 3 times more than Todd’s. Todd turned 120° on his board. How many degrees did Molly turn?
My Equation: _________________
Answer:
360°
Explanation:
Given,
Molly made a turn on her board that was 3 times more than Todd’s.
Todd turned 120° on his board.
3 × 120 = 360°
b. How many more degrees did Molly turn than Todd?
My Equation: _________________
Answer:
240°
Explanation:
Molly turned 240° than Todd.
360° – 120° = 240°
c. Teri turned 160° on her board. Lana made a turn that was 4 that much. How many degrees did Lana turn on her board?
My Equation: _________________
Answer:
40°
Explanation:
Given,
Teri turned 160° on her board.
Lana made a turn that was 4 that much.
160 ÷ 4 = 40°
d. How many more degrees did Teri turn than Lana?
My Equation: _________________
Answer:
120°
Explanation:
Teri turned 120° than Lana.
160 – 40 = 120°
e. Pablo made a 360° turn on his board. His brother, Marco, made a turn that was \(\frac{1}{6}\) of Pablo’s. How many degrees did Marco turn on his board?
My Equation: _________________
Answer:
60°
Explanation:
Pablo made a 360° turn on his board.
\(\frac{1}{6}\) of Pablo’s.
360 ÷ 60 = 60°
f. How many more degrees did Pablo turn than Marco?
My Equation: _________________
Answer:
300°
Explanation:
Pablo turned 300° than Marco.
360° – 60° = 300°
Question 2.
Solve the following pairs of multiplication problems.
\(\frac{1}{2}\) of 360 is _____________
\(\frac{1}{3}\) of 360 is _____________
\(\frac{1}{4}\) of 360 is _____________
\(\frac{1}{6}\) of 360 is _____________
\(\frac{1}{2}\) × 360 = _____________
\(\frac{1}{3}\) × 360 = _____________
\(\frac{1}{4}\) × 360 = _____________
\(\frac{1}{6}\) × 360 = _____________
Answer:
The pair of multiplication problems are 180, 120, 90, 60, 180, 120, 90, and 90.
Explanation:
\(\frac{1}{2}\) × 360 = 180
\(\frac{1}{3}\) × 360 = 120
\(\frac{1}{4}\) × 360 = 90
\(\frac{1}{6}\) × 360 = 60
\(\frac{1}{2}\) × 360 = 180
\(\frac{1}{3}\) × 360 = 120
\(\frac{1}{4}\) × 360 = 90
\(\frac{1}{6}\) × 360 = 90
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 4 Session 3 Answer Key
Mystery Angles
Question 1.
Find the measure of each of the mystery angles below. (Hint: If you remember that a right angle measures 90° and a straight angle measures 180°, you may be able to solve some of these problems without a protractor.)
a.
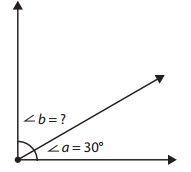
mystery angle b = ______________
Answer:
mystery angle b = 90°
Explanation:
Given,
∠a = 30° and we need to find ∠b
We know right angle measures 90°
∠a + ∠b = 90°
30° + ∠b = 90°
∠b = 90° – 30°
∠b = 60°
b.
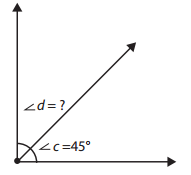
mystery angle d = ______________
Answer:
mystery angle d = 45°
Explanation:
Given,
∠c = 45 and we need to find ∠d
∠c + ∠d = 90°
45° +∠d = 90°
∠d = 90° – 45°
∠d = 45°
c.
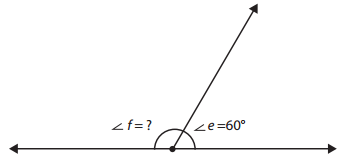
mystery angle f = ______________
Answer:
mystery angle f = 120°
Explanation:
Given,
∠e = 60 and we need to find ∠f
We know sum of angles in a straight line is 180°
∠f + ∠e = 180°
∠f + 60° = 180°
∠f = 180° – 60°
∠f = 120°
d.
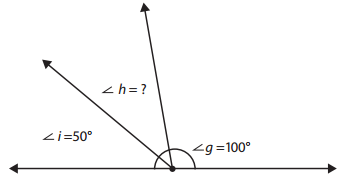
mystery angle h = ______________
Answer:
mystery angle h = 30°
Explanation:
Given,
∠i = 50, ∠g = 100 and we need to find ∠h
sum of angles in a straight line is 180
So,
∠i + ∠g + ∠h = 180°
50° + 100° + ∠h = 180°
150° + ∠h = 180°
∠h = 180° – 150°
∠h = 30°
Question 2.
Jami knows that when the clock says it’s exactly 1:00, the hands make an angle of 30°. What angle is formed by the hands on the clock when it’s exactly 5:00? Use numbers, labeled sketches, or words to explain your answer.
Answer:
The angle is formed by the hands on the clock when it’s exactly 5:00 is 150°.
Explanation:

Bridges in Mathematics Grade 4 Student Book Unit 5 Module 4 Session 4 Answer Key
Shapes & Angles
Question 1.
Using a protractor, sketch the following shapes with the correct angles.
a. a triangle with two 50° angles
Answer:
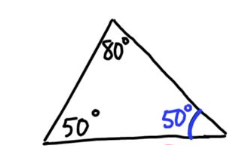
Explanation:
Given,
a triangle with two 50° angles.
We have drawn a traingle with wo 50° angles which is called scalene traingle.
b. a triangle with a right angle and 30° and 60° angles
Answer:
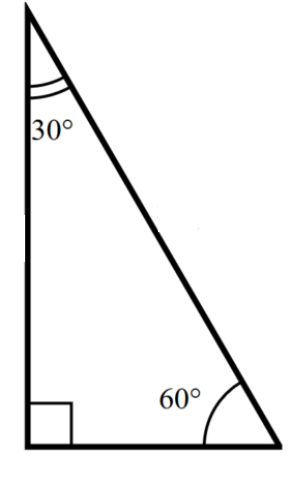
Explanation:
I have drawn a picture of a triangle with a right angle and 30° and 60° angles.
Question 2.
If a quadrilateral has angles that are all the same size, what name(s) might it have?
Answer:

Explanation:
A rectangle has angles that are all the same size.
Question 3.
If a quadrilateral has side lengths that are all the same size, what name(s) might it have?
Answer:
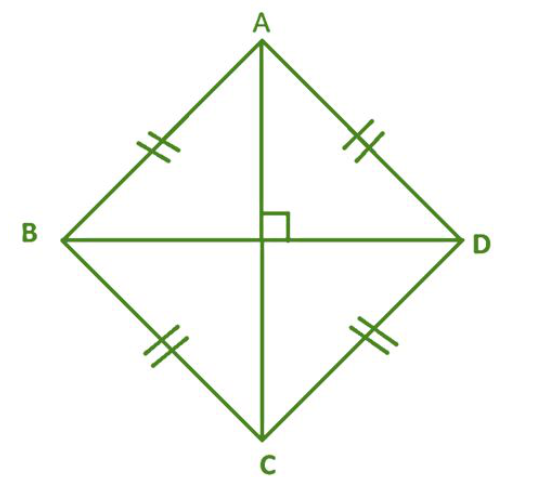
Explanation:
A rhombus is a quadrilateral with four equal sides.
Review
Question 4.
Is 7 a factor of 27?
Answer:
No, 7 is not a factor of 27.
Explanation:
As 7 is not divisible by 7.
Factors of 27 are 1, 3, 9, and 27.
Question 5.
Is 7 a factor of 41?
Answer:
No, 7 is not a factor of 41.
Explanation:
The number 41 is a prime number. As it can only be divided by 1 or itself. Hence the factors of 41 are 1 and 41.
Question 6.
Is 7 a factor of 49?
Answer:
yes, 7 is a factor of 49.
Explanation:
The factors of 49 are 1 and 7.
7 × 7 = 49
Question 7.
List the factors of 100.
Answer:
1, 2, 4, 5, 10, 20, 25, 50, and 100.
Explanation:
The list of factors that 100 has are
1, 2, 4, 5, 10, 20, 25, 50, and 100.