Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 4 Module 3 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 4 Module 3
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 3 Session 1 Answer Key
Rounded Measures
The book Hottest, Coldest, Highest, Deepest talks about the longest rivers on Earth. The length of each river is shown in the table below.
Question 1.
Round the river lengths to the nearest thousand, hundred, and ten. The first one is done for you.
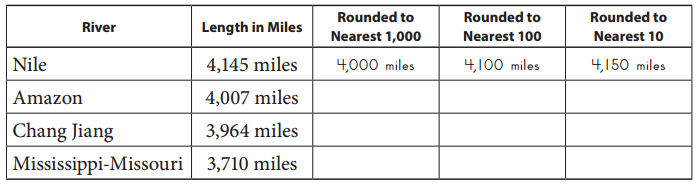
Answer:
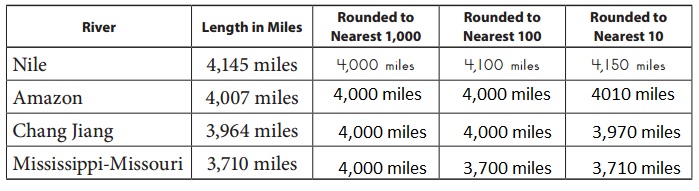
Explanation:
Rounded the river lengths to the nearest thousand, hundred, and ten above accordingly.
Question 2.
If the average rate of travel is 100 miles per day, about how long would it take to travel down each river in days? Write an equation to show. The first one is done for you. (Hint: Use the most useful rounded figure instead of the actual length.)

Answer:

Equation: Days = River length ÷ 100 miles,
Explanation:
Given if the average rate of travel is 100 miles per day, about how long would it take to travel down each river in days, an equation is days = river length ÷ 100 miles, So for Amazon it is
4,000/ 100 = 40 days, For Chang Jiang it is 4,000/ 100 = 40 days and for Mississippi – Missouri it is 3,700/ 100 = 37 days filled in the above table.
Question 3.
If the average rate of travel is 10 miles per hour, about how long would it take to travel down each river in hours? Write an equation to show. This first one is done for you.

Answer:

Explanation:
If the average rate of travel is 10 miles per hour long would it take to travel down each river in hours is Amazon it is 4,000/ 10 = 400 hours, For Chang Jiang it is 4,000/ 10 = 400 hours and for Mississippi – Missouri it is 3,700/ 10 = 370 hours filled in the above table.
Question 4.
Rounded to the nearest 10, about how much longer is the Nile than the Mississippi- Missouri? Show your work.
Answer:
440 miles,
Explanation:
Rounded to the nearest 10, about how much longer is the Nile than the Mississippi- Missouri is Nile is 4,150 miles and Mississippi- Missouri is 3,710 miles so long is 4,150 miles – 3,710 miles = 440 miles.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 3 Session 2 Answer Key
Which Race Was Run?
Use the Distance Challenge Flyer to answer the questions below. Make ratio tables to show your thinking.

Question 1.
How many meters would Kayla run if she entered the first and second races in the series?
Answer:
15,000 meters,
Explanation:
Meters would Kayla run if she entered the first and second races in the series is first race is 5k and second race is 10k total is 5k + 10 k = 15k as 1 kilometer = 1,000 meters it is 15 X 1,000 = 15,000 meters.
Question 2.
How many meters would Dana run if she entered the first four races in the series? (Note: 10 miles is approximately 16 kilometers.)
Answer:
49,000 meters,
Explanation:
Many meters would Dana run if she entered the first four races in the series is 5k + 10k + 10miles + 18k as 10 miles = 16 kilometers so it is 5k + 10k + 16k + 18k = 49 kilometers as 1 kilometer = 1,000 meters it is 49 X 1,000 = 49,000 meters.
Question 3.
If Roberto ran 18,000 meters, which race(s) did he run?
Answer:
Fourth race,
Explanation:
If Roberto ran 18,000 meters, which race(s) did he run is as 1,000 meters = 1 kilometer so
18,000 meters/1,000 meters = 18 k by using Distance Challenge Flyer it is fourth race.
Question 4.
If Matthew ran 48,000 meters, which two races did he run?
Answer:
30k – fifth race and 18k – third race,
Explanation:
If Matthew ran 48,000 meters two races did he ran are we can write 48,000 meters as 30,000 meters and 18,000 meters means 30,000/1,000 = 30k and 18,000/1,000 = 18k by using Distance Challenge Flyer it is 30k is fifth race and 18k is third race.
Work Place Instructions 4D Target Five
Each pair of players needs:
- 2 Target Five Record Sheets
- 2 dice numbered 1-6
- 3 dice numbered 4-9
1. Players decide who will go first. Player 1 rolls all 5 dice, one at a time. As the dice are rolled, Player 1 lines them up left to right to form a 5-digit target number. Both players write the target number in the box at the top of their Target Five Record Sheet.
2. Player 1 rolls all five dice and records the numbers in the first column of his record sheet. Player 1 then arranges those 5 digits to make a number that is as close as possible to the 5-digit target number, either under or over.
Andrew I rolled a 1, 6, 8, 5, and 1.
Miranda The target number is 68,729.
Andrew Wow! I really lucked out this time, because I got a 6 and an 8. That means I can make a number that starts with 68,000. I’ll put the 5 for 500, and then the two 1s. That’s as close as I can get.
3. Player 1 records the number in the second column and reads it aloud. Then in the third column, he finds the difference between his number and the target number, using the standard subtraction algorithm unless there’s another method that makes more sense.
Note Players need to show and check each other’s work during this game.
4. Finally, Player 1 records the difference between his number and the target number in the fourth column. That is his score for the first round. Player 2 takes a turn to complete steps 4-6.

5. Players continue to take turns until they have played 5 rounds. Then they add up their scores for each round to get a grand total. The player with the lower grand total wins the game.
6. After the game is finished, each player uses the >, =, or < symbol to compare her final score with her partner’s at the bottom of her record sheet, and then circles the winning score.
Game Variations
A. Students may choose to play Target Five together rather than playing against each other.
B. Students may choose to partner up, then play another pair competitively.
C. Students may choose a digit at the beginning of the game that, when rolled, acts as a wild number. If a player happens to roll that digit at the start of a turn, he can replace it with any digit he chooses, 0-9. This should improve his chances of making a 5-digit number that’s close to the target number.
Running Longer Distances
Question 1.
Make a ratio table to show your thinking.
a. Ava signed up to run a half marathon, which is approximately 21 kilometers. About how many meters will she run in the race?
Answer:
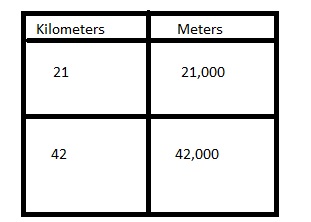
21,000 meters,
Explanation:
As Ava signed up to run a half marathon, which is approximately 21 kilometers as 1 kilometer = 1,000 meters so many meters will she run in the race 21 X 1,000 meters = 21,000 meters.
b. Bryan will run a full marathon. About how many meters will his race be?
Answer:
42,000 meters,
Explanation:
As Bryan will run a full marathon we have half marathon which is approximately 21 kilometers, So full marathon is 2 X 21 kilometers = 42 kilometers as 1 kilometer = 1,000 meters so many meters will he run in the race 42 X 1,000 meters = 42,000 meters shown a ratio table above.
Question 2.
Fill in the blank with the correct relational symbol: <, > or =.
a. 16 km ____ 16,000 meters
Answer:
16 km = 16,000 meters,
Explanation:
As 16 km in meters is as 1 kilometer is equal to 1,000 meters it is 16 X 1,000 meters = 16,000 meters which is same 16,000 meters only the correct relational symbol is equal so it is 16 km = 16,000 meters.
b. 1800 meters ____ 18 km
Answer:
1800 meters < 18 km,
Explanation:
As 18 km means 18 X 1,000 meters = 18,000 meters as 1,800 meters is less than 18,000 meters so 1800 meters < 18 km.
c. 13\(\frac{1}{2}\) km ___ 13,500 meters
Answer:
13\(\frac{1}{2}\) km = 13,500 meters,
Explanation:
Given 13\(\frac{1}{2}\) km first write in fraction so it is \(\frac{13 X 2 + 1}{2}\) km = \(\frac{27}{2}\) km as 1 km= 1,000 meters it is \(\frac{27}{2}\) X 1,000 meters = 27 X 500 meters = 13,500 meters which is equal so 13\(\frac{1}{2}\) km = 13,500 meters.
Question 3.
Complete the multiplication problems below.
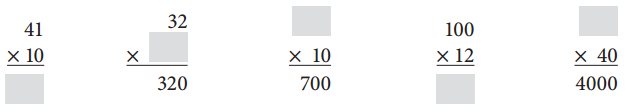
Answer:
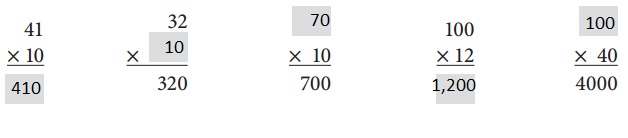
Explanation:
As 41 X 10 = 410, let’s take missing value as x so 32 X x = 320 so x = 320/32 = 10, x x 10 = 700 so x = 700/10 = 70, 100 X 12 = 1,200 and x X 40 = 4,000 so x = 4,000/40 = 100 completed the multiplication problems above.
Question 4.
Is \(\frac{4}{5}\) greater or less than \(\frac{45}{100}\)? How do you know?
Answer:
\(\frac{4}{5}\) is greater than \(\frac{45}{100}\),
Explanation:
Asking is \(\frac{4}{5}\) greater or less than \(\frac{45}{100}\) as both dont have common denominators we make both common denominators so we first multiply \(\frac{4}{5}\) both numerator and denominator by 20 \(\frac{4}{5}\) X \(\frac{20}{20}\) we get \(\frac{4 X 20}{5 X 20}\) = \(\frac{80}{100}\) as now both have common denominators we check with numerators 80 and 45 as 80 is greater than 45 so \(\frac{4}{5}\) is greater than \(\frac{45}{100}\),
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 3 Session 3 Answer Key
World Records
Question 1.
Use the Distance Challenge Flyer to solve the problems below. Use an open number line to model and solve each one.
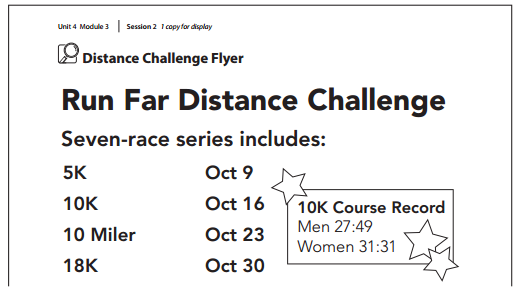
a. The world record for men in a 10K is 26:17. How much faster is this than the Distance Challenge course record?
Answer:
Faster is 1:32,
Explanation:
Given the world record for men in a 10K is 26:17. So much faster is this than the Distance Challenge course record is 27:49 – 26:17 = 1:32.
b. The world record for women in a 10K is 29:32. How much slower is the course record in the Distance Challenge?
Answer:
Slower is 1:59,
Explanation:
The world record for women in a 10K is 29:32. So much slower is the course record in the Distance Challenge is 31:31 – 29:32 as 1 minute is 60 seconds we convert 31:31 = 30:91, Now we subtract 30:91 – 29:32 = 1:59.
c. If a runner starts a race at 6:15 a.m. and runs for 75 minutes, what time does she stop running?
Answer:
7:30 am,
Explanation:
If a runner starts a race at 6:15 a.m. and runs for 75 minutes as we know 1 hour is 60 minutes,
so 75 minutes is 1:15 time does she stop running is 6:15 am + 1:15 = 7:30 am.
d. If a runner ended a race at 8:43 and ran for 73 minutes, what time did he start running?
Answer:
7:30,
Explanation:
If a runner ended a race at 8:43 and ran for 73 minutes as we know 1 hour = 60 minutes so 8:43 can be written as 7:103 therefore time did he start running is 7:103 – 73 = 7:30.
Question 2.
How many seconds are there in 3\(\frac{1}{2}\) minutes? Show your work.
Answer:
210 seconds,
Explanation:
Asking how many seconds are there in 3\(\frac{1}{2}\) minutes first we write mixed fraction into fraction as \(\frac{3 X 2 + 1}{2}\) minutes = \(\frac{7}{2}\) minutes as 1 minute is equal to 60 seconds we write as \(\frac{7}{2}\) X 60 seconds = 7 X 30 seconds = 210 seconds.
Question 3.
How many minutes are there in 5 hours? Show your work.
Answer:
300 minutes,
Explanation:
As 1 hour is equal to 60 minutes so 5 hours = 5 X 60 minutes = 300 minutes.
Preparing to Race
Question 1.
Use an open number line to model and solve each of these problems.
a. Jacob woke up at 5:50 a.m. on race day. He got ready in 35 minutes and drove 15 minutes to the event. Will he make it to the race for the 6:45 start time? Explain your thinking.
Answer:
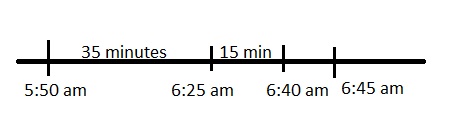
Yes he will make it to the race,
Explanation:
Given Jacob woke up at 5:50 a.m. on race day. He got ready in 35 minutes and drove 15 minutes to the event. Means 5:50 am + 35 minutes is 6:25am + 15 minutes = 6:40 am so yes he will make it to the race for the 6:45 start time.
b. During her practice this month, Briana ran one 10K in 1:02:18 and another in 58: 49. How much faster was her second 10K practice?
Answer:
Faster was her second 10K practice is 3:29,
Explanation:
During her practice this month, Briana ran one 10K in 1:02:18 and another in 58: 49. So much faster was her second 10K practice is 1 hour means 60 minutes so 1:02:18 is equivalent to 62:18 now minus 58:49 and 1 minute is equal to 60 seconds so it is 61:78 – 58:49 = 3:29.
c. Trevor needs to be at the starting line by 8:00 a.m. He needs 45 minutes to drive to the event, 20 minutes to eat breakfast, and 15 minutes to shower and dress. What time should he set his alarm so that he is on time for the race?
Answer:
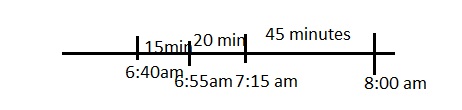
So time should he set his alarm so that he is on time for the race is 6:40 am,
Explanation:
Given Trevor needs to be at the starting line by 8:00 a.m. He needs 45 minutes to drive to the event, 20 minutes to eat breakfast, and 15 minutes to shower and dress. So he needs 45 minutes + 20 minutes + 15 minutes = 80 minutes means 1 hour 20 minutes so time should he set his alarm so that he is on time for the race is 8:00 am – 1:20 = 6:40 am.
Question 2.
Fill in the ratio tables.
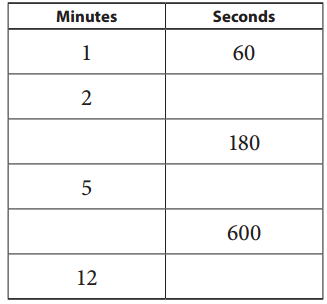
a.
Answer:
Explanation:
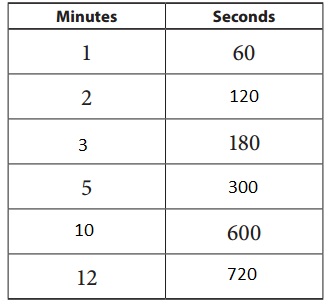
As 1 minute is 60 seconds, 2 minutes is 2 X 60 seconds = 120 seconds, 180 seconds means 180/60 = 3 minutes, 5 minutes = 5 X 60 = 300 seconds, 600 seconds means 600/60 = 10 minutes and 12 minutes means 12 X 60 seconds = 720 seconds filled in the ratio tables above.
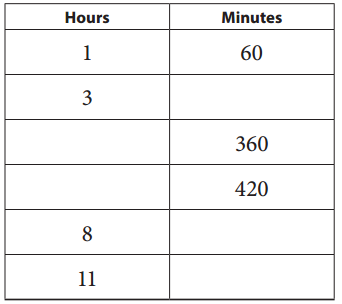
b.
Answer:
Explanation:
As 1 hour = 60 minutes, 3 hours = 3 X 60 = 180 minutes, 360 minutes = 360/60 = 6 hours,
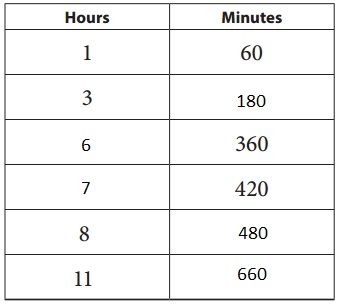
420 minutes = 420/60 = 7 hours, 8 hours = 8 X 60 minutes = 480 minutes, 11 hours = 11 X 60 minutes is 660 minutes filled in the ratio tables above.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 3 Session 4 Answer Key
Drinks for Runners
How much did each runner drink?
Visit each station and examine the measuring cup filled with water. Fill in the chart below with the volume of water each runner drank. Then answer the questions that follow.
Question 1.
How many milliliters did Runners D and J drink in all? How many liters?
Answer:
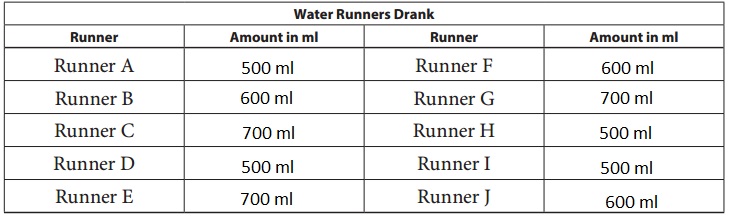
Runners D and J drank 1,100 milliliters of water, Liters 1.1,
Explanation:
As Runners D drank 500 ml and Runner J drank 600 ml total milliliters did Runners D and J drank in all is 500 ml + 600 ml = 1,100 ml as 1 liter = 1,000 ml so 1,100 ml means 1,100 liters/1,000 = 1.1 liters.
Question 2.
How many milliliters did Runners D, E, G, I, and J drink in all? How many liters?
Answer:
Runners D, E, G, I, and J drank in all is 3,000 milliliters, 3 liters,
Explanation:
Runners D, E, G, I, and J drank in all are 500 ml + 700 ml + 700 ml + 500 ml + 600 ml = 3,000 ml as 1 liter = 1,000 milliliters so 3,000 ml means 3,000 liters/1,000 = 3 liters.
Question 3.
How many milliliters did all 10 runners drink? How many liters?
Answer:
Milliliters did all 10 runners drank are 5,900 milliliters, 5.9 liters,
Explanation:
Number of milliliters did all 10 runners drank are Runner A to Runner J is 500 ml + 600 ml + 700 ml + 500 ml + 700 ml + 600 ml + 700 ml + 500 ml + 500 ml + 600 ml = 5,900 milliliters,
as 1 liter is equal to 1,000 ml so it is 5,900 liters/1,000 = 5.9 liters.
Liquid Intake
Question 1.
Each runner in the 5K race was given a liter of water to drink as she crossed the finish line. How many milliliters total were in the first 10 bottles handed out? Show your work.
Answer:
10,000 milliliters,
Explanation:
As each runner in the 5K race was given a liter of water to drink as she crossed the finish line. So many milliliters total were in the first 10 bottles handed out is 1 liter X 10 = 10 liters, as 1 liter is equal to 1,000 milliliters so 10 liters = 10 X 1,000 ml = 10,000 milliliters.
Question 2.
Carly bought a 2-liter bottle of water on the morning of her race. She drank 450 milliliters before the race began and 250 milliliters during the race. How much was left for after the race? Show your work.
Answer:
1,300 milliliters,
Explanation:
As Carly bought a 2-liter bottle of water on the morning of her race. She drank 450 milliliters before the race began and 250 milliliters during the race. Total she drank is 450 milliliters + 250 milliliters = 700 milliliters so much was left for after the race is as 2 liters – 700 ml and 2 liters means 2 X 1,000 milliliters – 700 ml = 1,300 milliliters.
Question 3.
Jon bought a 6-pack of sports drink bottles that each had a volume of 350 ml.
a. If Jon drank 4 of them, how many milliliters did he drink? Show your work.
Answer:
1,400 milliliters,
Explanation:
As Jon bought a 6-pack of sports drink bottles that each had a volume of 350 ml, if Jon drank 4 of them then milliliters did he drink is 4 X 350 ml = 1,400 milliliters.
b. How many more milliliters would Jon need to drink to have 2 liters? Show your work.
Answer:
600 milliliters,
Explanation:
As Jon drank 1,400 milliliters many more milliliters would Jon need to drink to have 2 liters is as 1 liter is equal to 1,000 ml so 2 liters means 2 x 1,000 ml = 2,000 ml therefore it is 2,000 ml – 1,400 ml = 600 milliliters.
Question 4.
Fill in the ratio table to convert liters to milliliters.

Answer:

Explanation:
Filled in the ratio table above to convert liters to milliliters as 1 liter = 1,000 ml for 2 liters it is 2 X 1,000 ml = 2,000 ml for 4,000 ml to liters it is 4,000/1,000 = 4 liters, for 5 liters it is 5 X 1,000 ml = 5,000 ml for 9,000 ml it is 9,000 liters/1,000 = 9 liters for 12 liters it is 12 x 1,000 ml = 12,000 milliliters above.
Question 5.
Fill in the blanks with the correct relational symbol: < , > , or =
a. 13,050 ____ 13,500
Answer:
13,050 < 13,500,
Explanation:
As 13,050 is less than 13,500 so used relational operator < so it is 13,050 < 13,500.
b. 600,000 + 50,000 + 3,000 + 20 + 9 ____ 653,209
Answer:
600,000 + 50,000 + 3,000 + 20 + 9 < 653,209,
Explanation:
As 600,000 + 50,000 + 3,000 + 20 + 9 = 65,3029 which is less than 653,209 so it is 600,000 + 50,000 + 3,000 + 20 + 9 < 653,209.
c. four hundred thousand, sixty two ___ 400,062
Answer:
four hundred thousand, sixty two = 400,062,
Explanation:
As four hundred thousand, sixty two = 400,062 is same as 400,62 so it is four hundred thousand, sixty two = 400,062.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 3 Session 5 Answer Key
Fueling Up
Use a ratio table to model and solve each of the problems below.
Question 1.
How many grams are equivalent to 12 kg?
Answer:
12,000 grams,
Explanation:
Many grams are equivalent to 12 kg is as 1 kg = 1,000 grams so 12 kg = 12 x 1,000 grams = 12,000 grams.
Question 2.
8 kilograms is equivalent to how many grams?
Answer:
8,000 grams,
Explanation:
As 1 kg = 1,000 grams so 8 kilograms is equal to 8 X 1,000 grams = 8,000 grams.
Question 3.
How many ounces are equivalent to 6 pounds?
Answer:
96 ounces,
Explanation:
As 1 pound is equal to 16 ounce so 6 pounds is equal to 6 X 16 = 96 ounces.
Question 4.
12 pounds is equivalent to how many ounces?
Answer:
192 ounces,
Explanation:
As 1 pound is equal to 16 ounce so 12 pounds is equal to 12 X 16 = 192 ounces.
Question 5.
Race organizers for the 10K need to feed twice as many runners as their original plan. If each runner gets 8 ounces of watermelon, how many ounces will they need to buy for 60 runners? How many pounds?
Answer:
480 ounces, 30 pounds,
Explanation:
Given Race organizers for the 10K need to feed twice as many runners as their original plan. If each runner gets 8 ounces of watermelon, So many ounces will they need to buy for 60 runners is 60 X 8 ounces = 480 ounces as 1 pound is equal to 16 ounce so 480 / 16 = 30 pounds.
More Food
Question 1.
Ryan bought 3 pounds of bananas to take to his race. When he returned home after his event, he put what was left on his kitchen scale. He discovered that he had eaten all but 13 ounces. How much did Ryan eat? Show your work.
Answer:
35 ounces,
Explanation:
As Ryan bought 3 pounds of bananas to take to his race. When he returned home after his event, he put what was left on his kitchen scale. He discovered that he had eaten all but 13 ounces. So Ryan eat as 1 pound = 16 ounces, 3 pounds = 3 X 16 ounces = 48 ounces, It is
48 ounces – 13 ounces = 35 ounces.
Question 2.
Liz, Dante, and Jasmine each ate 225 grams of oranges. How many more grams would the 3 of them need to eat to have eaten a kilogram of oranges? Show your work.
Answer:
775 grams,
Explanation:
As Liz, Dante, and Jasmine each ate 225 grams of oranges. So many more grams would the 3 of them need to eat to have eaten a kilogram of oranges is as 1 kilogram is equal to 1,000 grams it is 1,000 grams – 225 grams = 775 grams.
Question 3.
Fill in the ratio tables.
a.
Answer:
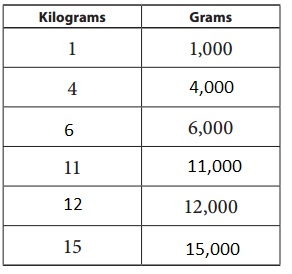
Explanation:
As 1 kilogram = 1,000 gram, 4 kilograms = 4 X 1,000 grams = 4,000 grams, 6,000 grams =
6,000/1,000 kilograms = 6 kilograms, 11 kilograms = 11 x 1,000 grams = 11,000 grams,
12,000 grams = 12,000 grams/1,000 = 12 kilograms and 15 kilograms = 15 x 1,000 grams = 15,000 grams filled in the ratio table above respectively.
b.
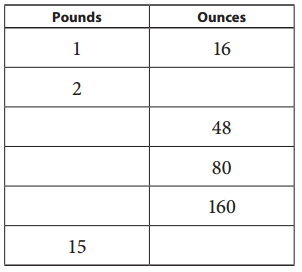
Answer:
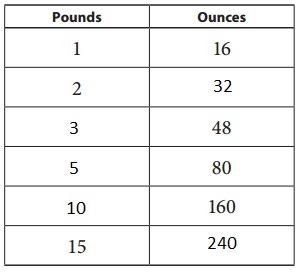
Explanation:
As 1 pound = 16 ounces, 2 pounds = 2 X 16 = 32 ounces, 48 ounces = 48/16 pounds = 3 pounds, 80 ounces = 80/16 pounds = 5 pounds, 160 ounces = 160/16 pounds = 10 pounds,
15 pounds = 15 X 16 ounces = 240 ounces filled in the ratio table above accordingly.