Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 4 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 4 Module 2
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 2 Session 1 Answer Key
How Old?
For each of the problems below, show your work. Hints:
- Think about whether the numbers in each problem lend themselves better to removal (take away) or finding the difference.
- Use labeled sketches of open number lines if you like.
Question 1.
Anna was born in 1997. How old was she in 2012?
Answer:
Anna is 15 years old,
Explanation:
Given Anna was born in 1997 so old was she in 2012 is 2012 – 1997 = 15 years.
Question 2.
Craig was born in 1992. How old was he in 2007?
Answer:
15 years old,
Explanation:
As Craig was born in 1992 old was he in 2007 is 2007 – 1992 = 15 years.
Question 3.
Peter was born in 1947. How old was he in 2000?
Answer:
53 years,
Explanation:
As Peter was born in 1947 old was he in 2000 is 2000 – 1947 = 53 years.
Question 4.
Peter’s wife, Sasha, was born in 1949. Is she older or younger than Peter? How old was she in 2000?
Answer:
She is younger than peter, 51 years,
Explanation:
Given Peter’s wife Sasha was born in 1949. As Peter was born in 1947, so 1947 – 1949 = 2 years she is 2 years younger than Peter, Now Sasha in 2000 is 2000 – 1949 = 51 years old.
Question 5.
Emma was born in 1963. How old was she in 2002?
Answer:
39 years old,
Explanation:
As Emma was born in 1963 old was she in 2002 is 2002 – 1963 = 39 years old.
Question 6.
Emma’s husband, Tom, was born in 1961. Is he older or younger than Emma? How old was he in 2002?
Answer:
Older than Emma, 41 years,
Explanation:
As Emma’s husband, Tom, was born in 1961 and Emma was born in 1963 so he is older by 1963 – 1961 = 2years so old was he in 2002 is 2002 – 1961 = 41 years.
Question 7.
If the telephone was invented in 1876, how “old” was it in 1991? (How long had it been around?)
Answer:
Long had it been around is 115 years,
Explanation:
If the telephone was invented in 1876 “old” was it in 1991 is 1991 – 1876 = 115 years.
Question 8.
If the stethoscope was invented in 1819, how old was it in 1997?
Answer:
178 years,
Explanation:
If the stethoscope was invented in 1819 old was it in 1997 is 1997 – 1819 = 178 years.
Question 9.
If the battery was invented in 1799, how old was it in 1998?
Answer:
199 years,
Explanation:
If the battery was invented in 1799 old was it in 1998 is 1998 – 1799 = 199 years.
Question 10.
CHALLENGE Fill in the blanks with any dates that make the sentence true.
a. Jon was born in ____ and was 39 years old in _______.
Answer:
Jon was born in 1975 and was 39 years old in 2014,
Explanation:
Lets take Jon was born in 1975 and was 39 years old in 1975 + 39 = 2014, So Jon was born in 1975 and was 39 years old in 2014.
b. Shelley was born in ____ and was 39 years old in ____.
Answer:
Shelley was born in 1978 and was 39 years old in 2017,
Explanation:
Lets take Shelley was born in 1978 and was 39 years old in 1978 + 39 = 2017, So Shelley was born in 1978 and was 39 years old in 2017.
c. Aaron was born in ____ and was 39 years old in ____.
Answer:
Aaron was born in 1972 and was 39 years old in 2011,
Explanation:
Lets take Aaron was born in 1972 and was 39 years old in 1972 + 39 = 2011, So Aaron was born in 1972 and was 39 years old in 2011.
Sam’s Subtraction Strategies
Sam’s fourth grade class is working on subtraction. Help Sam solve the problems below. Use whichever strategy works best for you.
Question 1.
Sam’s math teacher is 33. Sam is 9. How much older is Sam’s teacher than Sam?
Answer:
24 years old,
Explanation:
As Sam’s math teacher is 33. Sam is 9. Much older is Sam’s teacher than Sam is 33 – 9 = 24 years.
Question 2.
Sam’s art teacher is 51. How much older is Sam’s art teacher than his math teacher?
Answer:
Sam’s art teacher is 18 years than his math teacher,
Explanation:
Given Sam’s math teacher is 33 years and Sam’s art teacher is 51. So much older is Sam’s art teacher than his math teacher is 51 – 33 = 18 years old.
Question 3.
Sam has to solve the problem 91 – 76. Sam says it is easier to start at 91 and go back to 76 than to take 76 away from 91. Do you agree or disagree? Why?
Answer:
Disagree,
Explanation:
As Sam has to solve the problem 91 – 76. Sam says it is easier to start at 91 and go back to 76 than to take 76 away from 91. Yes I disagree as it is not easier to start at 91 and go back to 76 because we need to move one one step back from 76 to till 91 but it is rather very easy to take 76 at one time away from 91.
Review
Question 4.
Find each sum.
\(\frac{1}{10}\) + \(\frac{1}{100}\) =
\(\frac{5}{12}\) + \(\frac{3}{12}\) =
1\(\frac{1}{4}\) + 3\(\frac{3}{4}\) =
Answer:
\(\frac{11}{100}\),
\(\frac{8}{12}\) or \(\frac{2}{3}\),
5,
Explanation:
Asked to find sum \(\frac{1}{10}\) + \(\frac{1}{100}\) as denominators are not same we take common denominator as \(\frac{1X 10}{100}\) + \(\frac{1}{100}\) we get \(\frac{10 + 1}{100}\) = \(\frac{11}{100}\).
Now sum of \(\frac{5}{12}\) + \(\frac{3}{12}\) both have common denominators so we add numerators as \(\frac{5 + 3}{12}\) = \(\frac{8}{12}\) both goes in 4 we get \(\frac{4 x 2}{4 X 3}\) = \(\frac{2}{3}\).
Now sum of 1\(\frac{1}{4}\) + 3\(\frac{3}{4}\) both are in mixed fracttions we first convert them into fractions then add so \(\frac{1X 4 + 1}{4}\) + \(\frac{4 X 3 + 3}{4}\) = \(\frac{5}{4}\) + \(\frac{15}{4}\) both have common denominators so we add numerators as \(\frac{5 + 15}{4}\) = \(\frac{20}{4}\) as it goes in 4 (4 X 5 = 20) we get result as 5.
Question 5.
Find each difference.
2\(\frac{3}{8}\) – \(\frac{5}{8}\) =
\(\frac{3}{4}\) – \(\frac{1}{2}\) =
\(\frac{8}{10}\) – \(\frac{15}{100}\) =
Answer:
\(\frac{14}{8}\) or \(\frac{7}{4}\) or 1\(\frac{3}{4}\),
\(\frac{1}{4}\),
\(\frac{65}{100}\) or \(\frac{13}{20}\),
Explanation:
Asked to find the difference of 2\(\frac{3}{8}\) – \(\frac{5}{8}\) first we write the mixed fraction into fraction \(\frac{2 X 8 + 3}{8}\) – \(\frac{5}{8}\) =
\(\frac{19}{8}\) – \(\frac{5}{8}\) as both have common denominators we subtract numerators as \(\frac{19 – 5}{8}\) = \(\frac{14}{8}\) as both goes by 2 we get \(\frac{7 X 2}{4 X 2}\) = \(\frac{7}{4}\) as numerator is greater we write in mixed fraction as \(\frac{1 X 4 + 3}{4}\) = 1\(\frac{3}{4}\).
Now \(\frac{3}{4}\) – \(\frac{1}{2}\) as denominators are not the same first we make them common so \(\frac{3}{4}\) – (\(\frac{1}{2}\) X \(\frac{2}{2}\)) = \(\frac{3}{4}\) – \(\frac{2}{4}\) we have common denominator so we subtract numerators as \(\frac{3 – 2}{4}\) we get result as \(\frac{1}{4}\). Now \(\frac{8}{10}\) – \(\frac{15}{100}\) as denominators are not the same first we make them common as \(\frac{8 X 10}{10 x 10}\) – \(\frac{15}{100}\) = \(\frac{80}{100}\) – \(\frac{15}{100}\) now we subtract numerators as \(\frac{80 – 15}{100}\) = \(\frac{65}{100}\) as both numerator and denominator goes by 5 we get \(\frac{13 X 5}{20 X 5}\) = \(\frac{13}{20}\).
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 2 Session 2 Answer Key
Rolling Dice
Austin rolled six 4-9 dice. He arranged the dice and made these 3-digit numbers: 548 and 796.
Question 1.
What is the sum of Austin’s numbers? Use the strategy of your choice and show your work below.
Answer:
The sum is 1,344,
Strategy : Sum,
Explanation:
As Austin rolled six 4-9 dice. He arranged the dice and made these 3-digit numbers: 548 and 796. So the sum of Austin’s numbers is
796
+ 548
1,344 here I used strategy as sum.
Question 2.
What is the difference between Austin’s numbers? Use the strategy of your choice and show your work below.
Answer:
248,
Strategy: Difference,
Explanation:
As Austin rolled six 4-9 dice. He arranged the dice and made these 3-digit numbers: 548 and 796. So the difference between Austin’s numbers is
796
-548
248 here I used the strategy as difference.
Question 3.
What is the largest 6-digit number Austin can make with the numbers he rolled?
Answer:
The largest 6-digit number Austin can make is 987654,
Explanation:
As Austin rolled six 4-9 dice. He arranged the dice and made these 3-digit numbers: 548 and 796, So the largest among 5,4,8,7, 9 and 6 is 9 then 8 then 7 then 6 then 5 and then 4 so the largest 6 digit number is 987654.
Question 4.
What is the smallest 6-digit number Austin can make with the numbers he rolled?
Answer:
The smallest 6-digit number Austin can make is 546789,
Explanation:
As Austin rolled six 4-9 dice. He arranged the dice and made these 3-digit numbers: 548 and 796, So the smallest among 5,4,8,7, 9 and 6 is 4 then 5 then 6 then 7 then 8 and then 9 therefore the smallest 6-digit number Austin can make is 546789.
Question 5.
Austin rolled the dice again. This time he made these numbers: 467 and 594. Austin says he can add 460 and 601 and get the same sum as 467 and 594. Do you agree or disagree? Why?
Answer:
Yes I agree,
Explanation:
As Austin rolled the dice again. This time he made these numbers: 467 and 594. Austin says he can add 460 and 601 and get the same sum as 467 and 594 lets see 467 + 594 = 1,061 now we add 460 and 601 we get same sum as 1,061 therefore I agree.
Question 6.
Austin says he can find the difference between 467 and 594 by finding the difference between 473 and 600. Do you agree or disagree? Why?
Answer:
Yes I agree,
Explanation:
As Austin says he can find the difference between 467 and 594 by finding the difference between 473 and 600. So the difference between 594 and 467 is 127 and the difference between 473 and 600 is also 127 so I do agree.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 2 Session 3 Answer Key
More Practice with the Subtraction Algorithm
Latisha is figuring out information about the lives of her aunts and uncles. Help Latisha solve the problems below.
Question 1.
Latisha’s aunt was born in 1978. Latisha was born in 1999. How old was Latisha’s aunt when Latisha was born?
Answer:
21 years ,
Explanation:
As Latisha’s aunt was born in 1978. Latisha was born in 1999. So old was Latisha’s aunt when Latisha was born is 1999 – 1978 = 21 years.
Question 2.
Latisha’s uncle was born in 1975. He married Latisha’s aunt in 2003. How old was Latisha’s uncle when he got married?
Answer:
28 years,
Explanation:
Given Latisha’s uncle was born in 1975. He married Latisha’s aunt in 2003. So old was Latisha’s uncle when he got married is 2003 – 1975 = 28 years.
Question 3.
Latisha’s cousin was born in 2006. How old were Latisha’s aunt and uncle when her cousin was born?
Answer:
Latisha’s aunt is 28 years and uncle is at 31 years,
Explanation:
As Latisha’s cousin was born in 2006, Latisha’s aunt was born in year 1978 so Latisha’s aunt age when her cousin was born is 2006 – 1978 = 28 years and Latisha’s uncle was born in 1975 so old were Latisha’s uncle when her cousin was born is 2006 – 1975 = 31 years.
Question 4.
Choose two or more of the problems below to solve using the standard algorithm for subtraction. Show your work.

Answer:
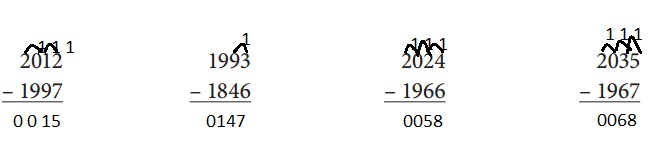
Explanation:
Using the standard algorithm for subtraction solved the above given problems.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 2 Session 4 Answer Key
Using Subtraction Strategies
Question 1.
Look at each subtraction problem below. Think about which strategy makes the most sense for each problem. Solve each problem.
a.
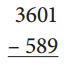
What strategy did you use? Why did you use this strategy?
Answer:
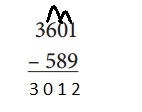
Strategy: Taking away,
Explanation:
Solved the above given problem, strategy I used is taking away 589 from 3,601 we get 3,012.
b.
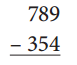
What strategy did you use? Why did you use this strategy?
Answer:
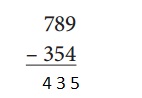
Strategy: Taking away,
Explanation:
Solved the above given problem, strategy I used is taking away 354 from 789 we get 435.
c.
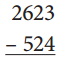
What strategy did you use? Why did you use this strategy?
Answer:
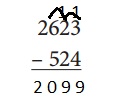
Strategy: Taking away,
Explanation:
Solved the above given problem, strategy I used is taking away 524 from 2623 we get 2099.
Question 2.
Fill in the blanks in the equations below:
621 – 589 = 632 – ____ 87 – ____ = 94 – 60
1005 – 896 = ___ – 900
Answer:
First one equation is wrong as 621 – 589 = 32 and 94 – 60 = 34 is not matching,
1,005 – 896 = 1,009 – 900,
Explanation:
As first one equation is wrong as 621 – 589 = 32 and 94 – 60 = 34 as 32 and 34 are not matching, Second one left side it is 1005 – 896 = 109 and right side it is 900 means 900 + 109 = 1,009 so the equation is 1,005 – 896 = 1,009 – 900.
Bridges in Mathematics Grade 4 Student Book Unit 4 Module 2 Session 5 Answer Key
Each pair of players needs:
- two 4C Roll & Subtract One Thousand Record Sheets
- 3 dice numbered 1-6
1. Each player labels a record sheet with the date and both players’ names. Players will keep track of their own results as well as those of their partner throughout the game.
2. Player 1 rolls the 3 dice and makes a 3-digit number with the digits rolled. Then she subtracts that number from 1,000, using the standard subtraction algorithm unless there’s another method that makes more sense. Player 2 also subtracts the number from 1,000 to check Player 1’s work, recording the results on his own record sheet.
3. Player 2 takes a turn to roll the dice, make a 3-digit number, and subtract it from 1,000.
Player 1 also subtracts the number from 1,000 to check Player 2’s work, recording the results on his own record sheet.
4. Players each take two more turns to roll and subtract 3-digit numbers from their total. Players share their strategies and check each other’s work after each turn.
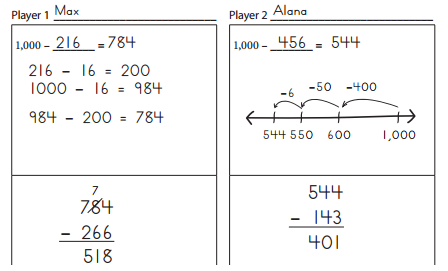
Max I really thought about the best way to do 784 – 266.1 finally picked the algorithm. Even though I had to cross out and borrow, it still seemed to be the easiest way.
Alana Taking away on the number line worked great for my first turn, but lining the numbers up and just subtracting on my second turn was really easy—no borrowing.
5. Players take one more turn each. After 3 turns each, the player with a total closest to 0 wins. If one player gets a negative number, the other player automatically wins the game.
6. Both players record two comparison statements at the bottom of their sheets using the symbols >, =, or <. Then they circle the player who is closest to 0 without going into negative numbers.
Game Variations
A. Players can play Roll & Subtract 250 by changing the heading and the first number on the record
sheet, and rolling 2 dice each time. The dice they use can. either be numbered 1-6, 4-9, or one of each.
B. Players can play Roll & Subtract 10,000 by changing the heading and first number on the record sheet, and rolling 4 dice each time. Players can also choose to use 1, 2, or 3 dice numbered 4-9 instead of using 4 dice all numbered 1-6 if they want.
C. Players can change the rules so they’re allowed to go into negative numbers. Then the player closest to 0
after 3 turns, either under or over, wins the game.
Helpful Hints
Question 1.
Jack has to solve the problem 281 – 266. How would you tell him to solve the problem? Tell which strategy you would use, and then solve the problem.
Answer:
By using taking away, 281 – 266 = 15,
Explanation:
Given Jack has to solve the problem 281 – 266. Strategy I would use, and then solve the problem is taking away 266 from 281 we get 15.
Question 2.
Zia has to solve the problem 311 – 287. How would you tell her to solve the problem? Tell which strategy you would use, and then solve the problem.
Answer:
By using taking away 311 – 287 = 24,
Explanation:
Given Zia has to solve the problem 311 – 287 strategy I would use is taking away 287 from 311 we get result as 24.
Question 3.
Randy has to solve the problem 358 – 247. He says it is easy to use the standard algorithm for this problem. Do you agree or disagree? Why?
Answer:
Yes I Agree, its simple and easy, result is 111,
Explanation:
Given Randy has to solve the problem 358 – 247. He says it is easy to use the standard algorithm for this problem. Yes I do agree its very simple and easy
358
-247
111.
Question 4.
Lani has to solve the problem 412 – 259. She says it is easy to use the standard algorithm for this problem. Do you agree or disagree? Why?
Answer:
Yes I Agree, its simple and easy, result is 153,
Explanation:
Given Lani has to solve the problem 412 – 259. She says it is easy to use the standard algorithm for this problem. Yes I do agree its very simple and easy as
1,1
412
-259
153
Question 5.
Put these numbers in order from least to greatest. Use relational symbols (<, >, =) between each pair of numbers.

Answer:

Explanation:
Kept the given numbers in order from least to greatest as 629,478 < 629,874 < 692,487 < 692,847 above.