Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 3 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 3
Bridges in Mathematics Grade 4 Student Book Unit 3 Module 3 Session 1 Answer Key
Decimals Are Fractions
Question 1.
Write the decimal and fraction for each collection in the table below.
a.
collection
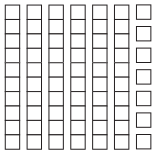
Decimal
Fraction
Answer:
Decimal : 0.67
Fraction : \(\frac{67}{100}\)
b.
collection

Decimal
Fraction
Answer:
Decimal : 0.12
Fraction : \(\frac{12}{100}\)
c.
collection
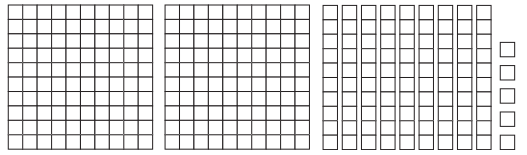
Decimal
Fraction
Answer:
Decimal : 2.95
Fraction : 2\(\frac{95}{100}\)
d. collection
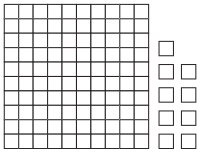
Decimal
Fraction
Answer:
Decimal : 1.09
Fraction : 1\(\frac{9}{100}\)
Question 2.
Sketch base ten pieces to show the minimal collection for each decimal. Then, write the number as a fraction. (A minimal collection is one that uses the fewest possible number of pieces.)
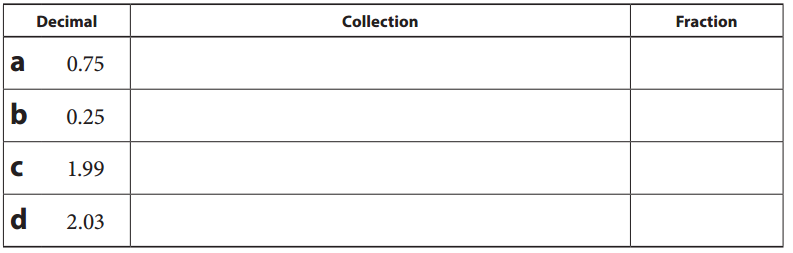
Answer:
0.75 :

![]()
Fraction: \(\frac{75}{100}\)
0.25:
![]()
![]()
Fraction: \(\frac{25}{100}\)
1.99:


![]()
Question 3.
Write the numbers 0.75, 0.25, 1.99, and 2.03 in their approximate places on the number line below.

Answer:

Question 4.
The value of the mat is 1.

a. How many tenths are shaded on the mat?
Answer: 4
Total number of tenths = 10
Number of tenths unshaded = 6
Therefore, total number of shaded tenths = 10 -6 =4
b. How many hundredths are shaded on the mat? How do you know?
Answer: 40
Total number of hundredths = 100
number of hundredths shaded = 40
Therefore, the number of hundredths that are shaded on the mat = 40
c. Write two fraction names for the shaded amount.
Answer: \(\frac{4}{10}\), \(\frac{40}{100}\)
The two fractions that are for the shaded amount = \(\frac{4}{10}\), \(\frac{40}{100}\) .
Because the total number of rows that are shaded = 4
d. Write two decimal names for the shaded amount.
Answer: 0.4 and 0.399
The two decimals that are for the shaded amount = 0.4 and 0.399
Because the total number of rows that are shaded = 4
Question 5.
Use numbers, words, or sketches to record at least two different observations about decimals and fractions.
Answer:
3.18:



![]()
![]()
4.68:





![]()
Money, Decimals & Fractions
Question 1.
Sketch base ten pieces to show the value of each number.
a. 3.18
b. 4.68
Answer:
3.18:



![]()
![]()
4.68:





![]()
Question 2.
Write a decimal number for each collection of base ten area pieces below.
a.
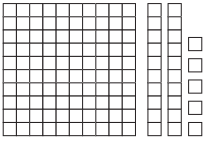
Answer: 1.25
In the above figure, 1 complete mat is there along with 25 hundredths.
Therefore, the decimal number for the above figure is 1.25
b.

Answer: 2.23
In the above figure, 2 complete mats are there along with 13 hundredths.
Therefore, the decimal number for the above figure is 2.23
Question 3.
Fill in the table to show each value as money, a decimal, or a fraction.
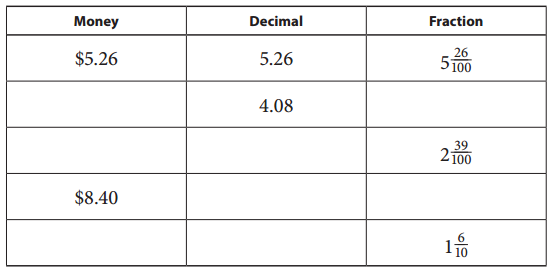
Answer:
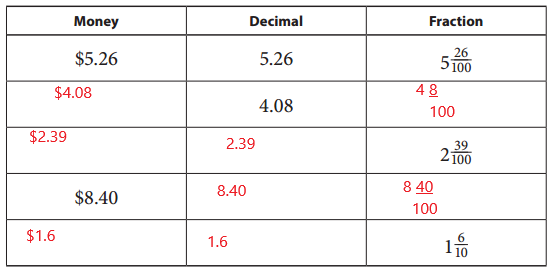
Question 4.
Write this number as a decimal: one and fifty-six hundredths.
Answer: 1.56
given number is one and fifty- six hundredths which is equivalent to 1.56 decimal number.
Question 5.
Write this decimal number in words: 2.94.
Answer: two and ninety-four hundredths
Given decimal number is 2.94 which is equivalent to two and ninety-four hundredths.
Comparing Decimals & Fractions
For all questions below, write an inequality using the symbols < or > to show your answer.
Question 1.
Two baby hummingbirds hatched last week at the zoo. A researcher is keeping track of their weights. Today Baby A weighs 1.2 grams and Baby B weighs 1.09 grams. Which is heavier, Baby A or Baby B?
Answer: Baby A is heavier than Baby B
Baby A > Baby B
Baby A weight = 1.2 grams
Baby B weight = 1.09 grams
As 1.2 is greater than 1.09. Hence, baby A is greater than baby B.
Question 2.
Rosario and her friend Keiko walked in the walkathon to benefit the animal shelter. Rosario walked 3.41 miles, and Keiko walked 3.8 miles. Who walked farther?

Answer: Keiko walked farther.
Distance walked by Rosario = 3.41 miles
distance walked by Keiko = 3.8 miles
As 3.8 miles is greater than 3.41. Hence Keiko walked farther than Rosario.
Question 3.
A giant panda at the Beijing Zoo in China had twins named Lucy and Lei. Giant pandas can weigh over 200 pounds when fully grown, but they have very tiny babies. When they were born, Lei weighed 5.29 ounces and Lucy weighed 5.9 ounces. Which twin was heavier?

Answer: Lucy was heavier.
Lei weighed = 5.23 ounces
Lucy weighed = 5.9 ounces
As 5.9 is greater than 5.23. Hence Lucy weight is more than Lei.
Question 4.
Which fraction is larger: \(\frac{6}{10}\) or \(\frac{49}{100}\)?
a. Explain why you think so.
Answer: \(\frac{6}{10}\)
\(\frac{6}{10}\)= 0.6
\(\frac{49}{100}\) = 0.49
As 0.6 is greater than 0.49. Hence \(\frac{6}{10}\) is larger than \(\frac{49}{100}\)
b. Draw each fraction on a grid below to verify your answer.
Answer:
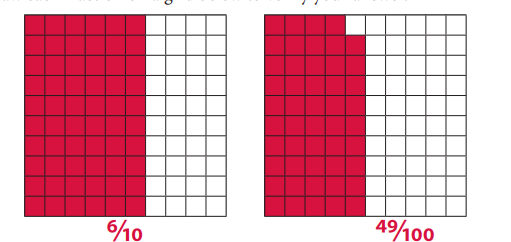
c. Record each fraction as a decimal number.
\(\frac{6}{10}\) , \(\frac{49}{100}\)
Answer:
\(\frac{6}{10}\) = 0.6
\(\frac{49}{100}\) = 0.49
Question 5.
a. On each grid below: shade in and label a different number between 0.45 and 0.5.
Answer:
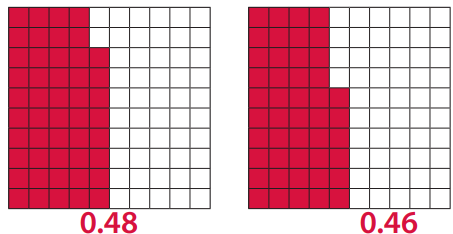
b. Compare the numbers. Write an inequality using the symbol < or > to show which number is larger.
Answer: 0.46 < 0.48
As 0.46 is lesser than 0.48. Hence 0.48 is greater than 0.46.
Bridges in Mathematics Grade 4 Student Book Unit 3 Module 3 Session 2 Answer Key
Number Riddles
Question 1.
Draw a line to show which number matches each description. This first one has been done for you as an example.

Answer:

Question 2.
Write each number in words.
a. 1.89
Answer: one and eighty nine hundredths
Explanation: After decimal point 89 (eighty nine) is there which is expressed in eighty nine hundredths.
b. 2.03
Answer: two and three hundredths
After decimal 3 (three) is there which is expressed in three hundredths.
c. Use a symbol (<, >, =) to compare these numbers: 1.89 ___ 2.03.
Answer: 1.89 < 2.03
2.03 is greater than 1.89. Therefore, 1.89 < 2.03.
Question 3.
Write each number as a decimal and a mixed number:
a. Three and eighty-three hundredths ____ _____
Answer:
Decimal : 3.89
Fraction : 3\(\frac{83}{100}\)
b. Four and six hundredths ____ _____
Answer:
Decimal: 4.06
Fracion: 4\(\frac{6}{100}\)
c. Use a symbol (<, >, =) to compare the two numbers in 3a and 3b.
____ ___ ____
Answer: 3.83< 4.06
3.83 is less than 4.06. Hence, 3.83 < 4.06.
Question 4.
CHALLENGE Write an even number that has a 7 in the hundreds place, an odd number in the thousands place, and is a multiple of 10.
Answer: 3750
Given that,
In hundreds place the number is 7. And in thousands place the number is odd. Here I am taking odd number as 3. And also mentioned the number is even number which is the multiple of 10.
Bridges in Mathematics Grade 4 Student Book Unit 3 Module 3 Session 3 Answer Key
Work Place Instructions 3C Decimal Four Spins to Win
Each pair of players needs:
- 2 Decimal Four Spins to Win Record Sheets
- 1 set of base ten area pieces
- 1 spinner overlay
- colored pencils or crayons in several different colors
1. Players spin the second (hundredths) spinner on the record sheet. The player with the larger fraction goes first.
2. Player 1 spins both spinners and records the results in his Spin 1 box. Then he:
- Rewrites the first fraction as an equivalent fraction with denominator 100
- Adds the two fractions
- Shows the answer as a fraction and as a decimal
- Colors in the first grid to show the results of his spin
Pedro OK, I got \(\frac{2}{10}\) and \(\frac{49}{100}\)– I know \(\frac{2}{10}\) is the same as \(\frac{20}{100}\), so I’ll write that and add my fractions. It’s \(\frac{69}{100}\) in all. Now I have to color in the first grid to show what I got.
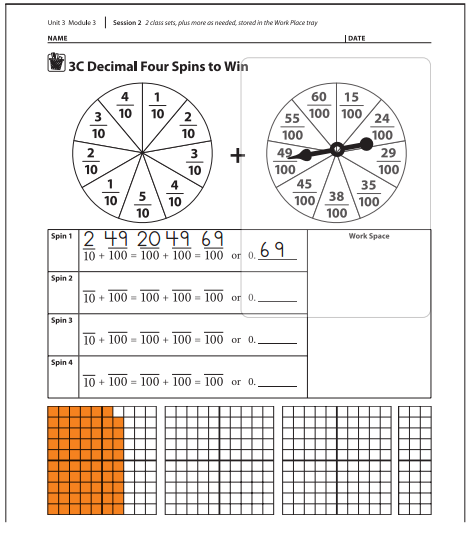
3. Player 2 takes a turn to spin, record, add, and color in the results on her record sheet.
4. Players take turns until they have each had 4 turns.
- Players must be sure to use a different color to shade in their grids each time they take a turn.
- It’s OK to go over 3.00. (That’s what the 3 extra tenths at the end of row of grids are for; don’t use them unless you have to.)
5. After each player has taken four turns, they each find their total and record it on their sheet.
Note It’s a very good idea to double-check the totals. If a player found the total by looking at her grids, she should also use the work space on her sheet to add the four decimal numbers. (It’s fine to use the base ten pieces to help add these numbers.)
6. Players each record their partner’s total, compare the two, and circle the total that’s closer to 3.00, either under or over.
Game Variation
A. Players work together, using one record sheet, to see how close they can come to 3.00, instead of playing competitively. (They can play the game twice and see if they can get closer to 3.00 the second time.)
B. Players use the rule that they can’t go over 3.00. If they play using this variation, they don’t have to take all 4 turns. They can decide to hold at 3 turns if it looks like a fourth turn might take them over 3.00. This variation is scored the same way as the regular version-players find their totals, and the score closer to 3.00 wins.
Tenths & Hundredths
Question 1.
Each grid below has a value of 1.0. Write two fractions and two decimals to show the amount shaded in on each.
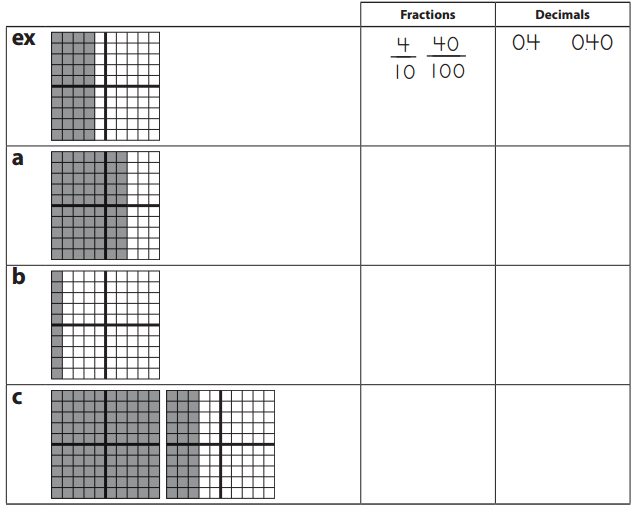
Answer:
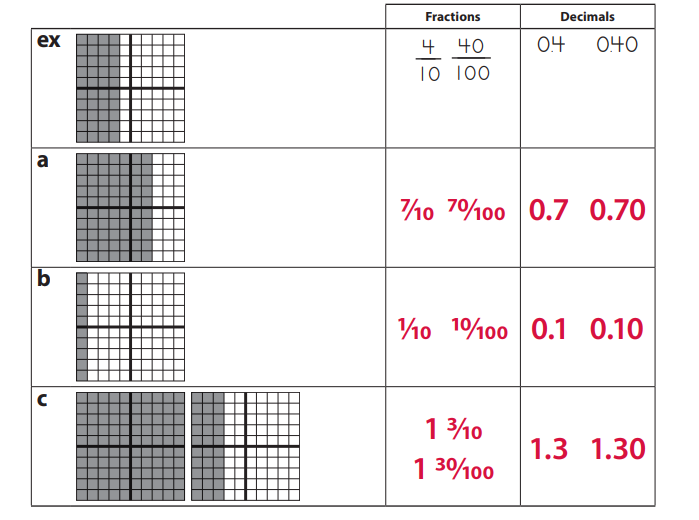
Question 2.
Rewrite each fraction as an equivalent fraction with denominator 100. (The first one is done for you.)
\(\frac{2}{10}\) = \(\frac{20}{100}\) \(\frac{9}{10}\) = \(\frac{1}{10}\) = \(\frac{8}{10}\) = \(\frac{5}{10}\) =
Answer:
\(\frac{2}{10}\) = \(\frac{20}{100}\)
\(\frac{9}{10}\) = \(\frac{90}{100}\)
\(\frac{1}{10}\) = \(\frac{10}{100}\)
\(\frac{8}{10}\) = \(\frac{80}{100}\)
\(\frac{5}{10}\) = \(\frac{50}{100}\)
Question 3.
Add these pairs of fractions. Express the answer for each as a fraction with denominator 100.
\(\frac{2}{10}\) + \(\frac{35}{100}\) = \(\frac{9}{10}\) + \(\frac{6}{100}\) = \(\frac{1}{10}\) + \(\frac{89}{100}\) = \(\frac{8}{10}\) + \(\frac{13}{100}\)
Answer:
\(\frac{2}{10}\) + \(\frac{35}{100}\) = \(\frac{20}{100}\) + \(\frac{35}{100}\) = \(\frac{55}{100}\)
\(\frac{9}{10}\) + \(\frac{6}{100}\) = \(\frac{90}{100}\) + \(\frac{6}{100}\) = \(\frac{96}{100}\)
\(\frac{1}{10}\) + \(\frac{89}{100}\) = \(\frac{10}{100}\) + \(\frac{89}{100}\) = \(\frac{99}{100}\)
\(\frac{8}{10}\) + \(\frac{13}{100}\) = \(\frac{80}{100}\) + \(\frac{50}{100}\) = \(\frac{130}{100}\)
Bridges in Mathematics Grade 4 Student Book Unit 3 Module 3 Session 4 Answer Key
Work Place Instructions 3D Decimal More or Less
Each pair of players needs:
- 2 Decimal More or Less Record Sheets
- 2 sets of base ten area pieces
- 1 spinner overlay
- 1 more/less die
1. Players roll the more/less die to determine whether they will play for more or less in the first round. They circle the word more or less on their record sheets to show.
2. Players spin the Decimal More or Less Spinner. The player with the larger number goes first.
3. Player 1 spins the spinner and decides whether to place the number in the ones, tenths, or hundredths place. Both players write Player 1’s number on their record sheets.
Note Once a number has been placed, it cannot be moved.
4. Then Player 1 sets out base ten area pieces to show the value of the number spun.
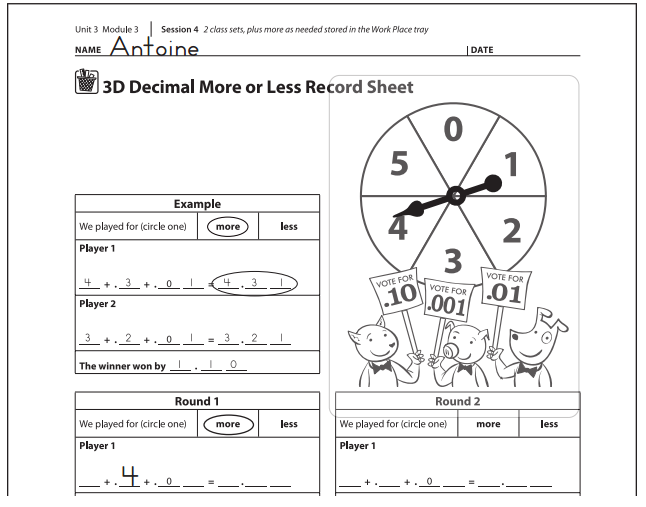
Antoine I got a 4, so I put it in the tenths place. We’re playing for more, so I could still get a 5 to put in the ones place. I put out 4 strips to show four-tenths.
5. Players take turns until they have each taken 3 spins. After each spin, the player decides where to place the new number and sets out base ten area pieces to show the value of the number.
6. After each player has taken three turns, players find the sum of their numbers and record it on their sheets.
7. Players read their numbers aloud and compare them.
8. Depending on what was rolled at the beginning of the round, the player with the higher or lower sum wins that round. Both players mark the winner for the round on their record sheets.
9. Players start the next round by rolling the more/less die again, and continue playing until they have completed all four rounds on the sheet.
Game Variation
A. Players determine how much the winner won by each time and use the difference between the numbers as a score. After four rounds, players add their scores and then roll the more/less die to determine the overall winner.
Decimal More or Less Challenges
Question 1.
Allen played Decimal More or Less with the record sheet below. He spun a 1 on his second turn. Where should Allen place the 1? Explain your thinking.
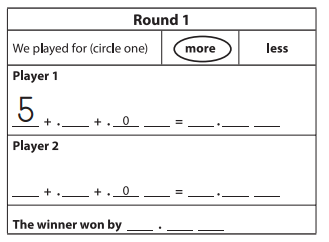
Answer:
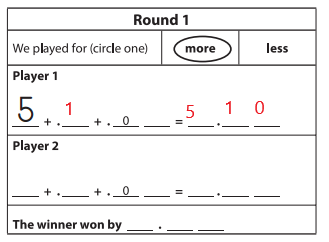
He spun a 1 on his second turn.
Therefore, placing one after decimal.
Question 2.
Kathy (Player 1) and Logan (Player 2) played Decimal More or Less with the record sheet below. Who won? By how much? Show your work.
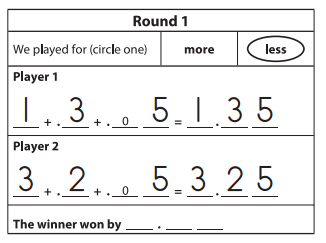
Answer: player 2 won the game
Player 1 score : 1.35
Player 2 score : 3.25
player 2 won by 1.90 (3.25 – 1.35) than player 1.
Question 3.
Fill in the blanks with the correct symbols. (< , > , =)
a. 3 km ____ 3000 m
Answer: 3 km = 3000 m
1 km = 1000 m
therefore 3 km= 3 x 1000 = 3000 m
So, 3km = 3000 m
b. 1.5 ml ___ 1500 l
Answer: 1.5 ml < 1500 l
1 liter = 1000 ml
1.5 ml = 0.0015 l
Therefore, 0.0015 is less than 1500. So, 0.0015 < 1500
c. 10.4 ____ 10.09
Answer: 10.4 > 10.09
10.4 is greater than 10.09 according to their hundredths position.
Question 4.
Here is part of a ratio table Becky made. Use it to answer the following questions:

a. What number is Becky counting by? ______
Answer: 13
The number that Becky counting is 13. Each time he is adding 13 to the previous number to get the result.
b. What will be the 24th number on Becky’s table? _____
Answer: 312
Given 19th number = 247
required 24th number = ?
24th number = 19th number + (13 x (24 – 19))
24th number = 247 + (13 x 5)
24th number = 312
c. What will be the 30th number on Becky’s table? ______
Answer: 390
Given 19th number = 247
required 30th number = ?
30th number = 19th number + (13 x (30 – 19))
30th number = 247 + (13 x 11)
30th number = 390