Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 2 Module 3 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 2 Module 3
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 1 Answer Key
Riley’s & Raymond’s Ratio Tables
Question 1.
Riley made a ratio table, but you can only see this part of it.
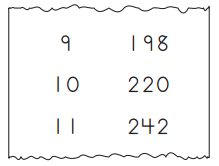
a. What number did Riley use to make her ratio table? _______
Answer:
9:198
= 198/9 = 22
So, Riley use 22 to make her ratio table.
b. What is the 13th row? ______
Answer:
1st row is 1:22
13th row = 22 × 13 = 286
So, 13th row is 286.
c. What is the 5th row? ______
Answer:
1st row is 1:22
5th row = 5 × 22 = 110
So, the 5th row is 110.
Question 2.
Raymond made a ratio table, but you can only see this part of it.

a. What number did Raymond use to make his ratio table? _____
Answer:
The ratio is 17 : 306
306/17 = 18
The number is 18.
Thus Raymond use 18 to make his ratio table.
b. What is the 10th row? ______
Answer:
1st row is 1 : 18.
10th row is 18 × 10 = 180
So, the 10th row is 180.
c. What is the 22nd row? _____
Answer:
1st row is 1 : 18.
22nd row is 22 × 18 = 396.
So, the 22nd row is 396.
Question 3.
CHALLENGE The area of a rectangle is 280 and one dimension is 14. What is the other dimension?
Answer:
Given,
The area of a rectangle is 280 and one dimension is 14.
We know that,
Area of the rectangle = l × w
280 = 14 × w
w = 280/14
w = 20
So, the other dimension is 20.
Maggie’s Chickens
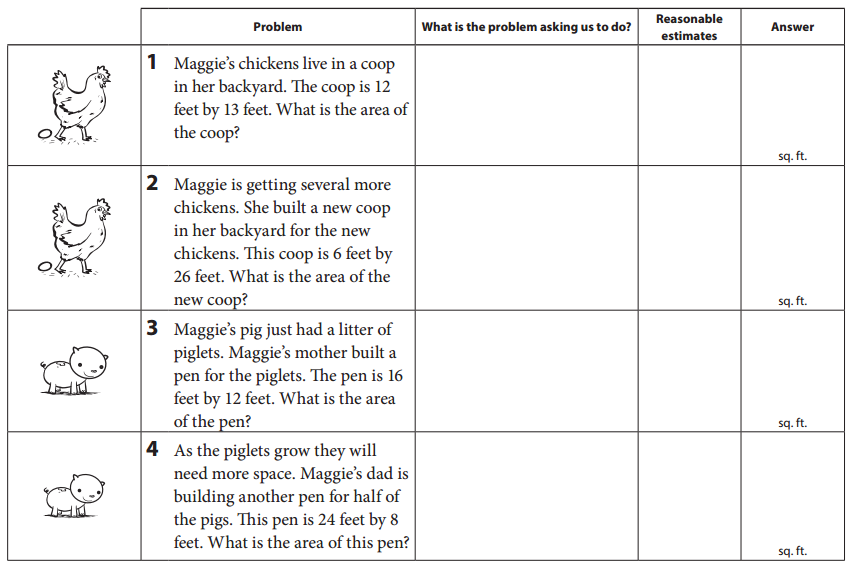
Answer:
1. Given,
Maggie’s chickens line in a coop in her backyard.
The coop is 12 feet by 13 feet.
We know that,
Area of the rectangle = l × w
A = 12 × 13
A = 156 sq. ft
2. Maggie is getting several more chickens.
The coop is 6 feet by 26 feet.
We know that,
Area of the rectangle = l × w
A = 6 × 26
A = 156 sq. ft
3. Maggie’s pig just had a litter of piglets.
The pen is 16 feet by 12 feet.
We know that,
Area of the rectangle = l × w
A = 16 × 12
A = 192 sq. ft
4. As the piglets grow they will need more space.
Maggie’s dad is building another pen for half of the pigs.
This pen is 24 feet by 8 feet.
We know that,
Area of the rectangle = l × w
A = 24 × 8
A = 192 sq. ft

Eggs & Apples
Read each problem and estimate the answer. Think about familiar strategies that will help you solve the problems. Show your work using numbers, labeled sketches, or words.
Question 1.
Maggie has 15 chickens. Each chicken lays 24 eggs a month. How many eggs do Maggie’s chickens lay in a month in all?
a. My estimate: ______
Answer:
Given,
Maggie has 15 chickens.
Each chicken lays 24 eggs a month.
Estimated number of eggs is 300.
b. My work:
Maggie’s chickens lay ____ eggs in a month altogether.
Answer:
Given,
Maggie has 15 chickens.
Each chicken lays 24 eggs a month.
1 chicken = 24 eggs
15 chickens = 15 × 24 = 360 eggs
Maggie’s chickens lay 360 eggs in a month altogether.
c. What strategy did you use? Why did you choose this strategy?
Answer: We used multiplication strategy to find number of eggs Maggie’s chicken lay in one month altogether.
Question 2.
Maggie is picking apples for her chickens. She has 12 baskets. She puts 30 apples in each basket. How many apples does Maggie pick in all?
a. My estimate: _____
Answer:
Given,
Maggie is picking apples for her chickens.
She has 12 baskets. She puts 30 apples in each basket.
10 × 30 = 300 apples.
So, my estimate is 300 apples.
b. My work:
Maggie picks ____ apples in all.
Answer:
Given,
Maggie is picking apples for her chickens.
She has 12 baskets.
She puts 30 apples in each basket.
12 × 30= 360 apples.
Maggie picks 360 apples in all.
c. What strategy did you use? Why did you choose this strategy?
Answer: We used the multiplication strategy to find a number of eggs Maggie’s chicken lay in one month altogether.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 2 Answer Key
Mario’s Marbles
Mario loves marbles and is always adding new marbles to his collection. Help Mario keep track of his marbles in the following problems. Show your work using numbers, labeled sketches, or words. Write a multiplication equation for problems 1 and 2.
Question 1.
Mario organized some of his marbles. He used lots of marbles to make 11 piles. Each pile had 14 marbles. How many marbles did he use in all?
Equation: ________________
Answer:
Given,
Mario organized some of his marbles.
He used lots of marbles to make 11 piles.
Each pile had 14 marbles.
14 × 11 = 154 marbles
Thus he use 154 marbles in all.
Question 2.
Mario organized the rest of his marbles. He made 7 piles and put 22 marbles in each pile. How many marbles did he use in all?
Equation: ______
Answer:
Given,
Mario organized the rest of his marbles.
He made 7 piles and put 22 marbles in each pile.
7 × 22 = 154 marbles
Thus he use 154 marbles in all.
Question 3.
Mario saw bags of marbles for sale at the store. One bag had 49 marbles in it. Mario wondered if he could organize the 49 marbles into equal piles.
a. Is 49 prime or composite?
Answer:
49 = 7 × 7
The factors of 49 are 1, 7, 49.
So, 49 is a composite number.
b. Can Mario organize his marbles into equal piles? Explain your answer.
Answer:
Given,
Mario saw bags of marbles for sale at the store.
One bag had 49 marbles in it. Mario wondered if he could organize the 49 marbles into equal piles.
49/7 = 7
Yes, Mario can organize his marbles into equal piles.
Question 4.
Another bag of marbles has 61 marbles in it. Mario wondered if he could organize the 61 marbles into equal piles.
a. Is 61 prime or composite?
Answer:
61 is a prime number.
b. Can Mario organize his marbles into equal piles? Explain your answer.
Answer:
Given,
Another bag of marbles has 61 marbles in it. Mario wondered if he could organize the 61 marbles into equal piles.
No Mario cannot organize his marbles into equal piles.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 3 Answer Key
How Can You Solve … ?
Corinne is in fourth grade and she has to solve a lot of math problems. Help Corinne solve the following problems.
Question 1.
Corinne has to solve 10 × 8 and 5 × 16.
a. What observations can you share with Corinne about these problems to help her solve them?
Answer: We observe that the product of two questions are the same.
b. How would you tell or show Corinne how to solve these problems?
Answer:
The product of 10 and 8 can be calculated by writing one zero to the right of 8. It becomes 80.
The product of 5 and 16 can be calculated by dividing 16 by 2 and then multiply the result by 10.
16 × 5
16 × 10/2
= 16/2 × 10
= 8 × 10
= 80
c. Solve 10 × 8 and 16 × 5.
Answer:
10
×8
80
16
×5
80
Question 2.
Corinne has to solve 12 × 9 and 18 × 6.
a. What observations can you share with Corinne about these problems to help her solve them?
Answer: We observe that the product of two questions are the same.
b. How would you tell or show Corinne how to solve these problems?
Answer:
12 × 9 = 108
18 × 6 = 108
c. Solve 12 × 9 and 18 × 6.
Answer:
12
×9
108
18
×6
108
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 4 Answer Key
Work Place Instructions 2C Moolah on My Mind
Each pair of players needs:
- 2 dice numbered 1-6
- spinner overlay
- a 2C Moolah on My Mind Record Sheet for each player
1. Players take turns rolling one die. The player with the higher number goes first.
2. Player 1 rolls both dice, adds the two numbers, and then spins the coin spinner.
3. Player 1 writes an expression in the first column to show the results of the rolls and spin.
4. Player 1 multiplies to find out how much money she collected and writes that amount in the second column. Then Player 1 writes it again in the last column so she can keep a running total of her money.
5. Then it is Player 2s turn. Player 2 repeats Steps 3, 4, and 5.
6. Players help each other make sure they are adding their money accurately and that each other’s running totals are correct.
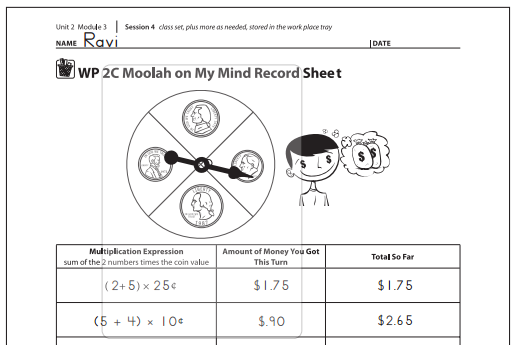
7. When both players have taken 10 turns, the game is over and the player with the most money wins.
Game Variations
A. The player with the least amount of money at the end of the game wins.
B. Pick two numbers and call them “take-aways.” For example, a player’s take-aways could be 4 and 7.
If two numbers are rolled that add up to one of the “take-aways” (such as 3 + 4 = 7), the player spins the coin spinner, multiplies the coin value by the take-away number, and takes that amount of money away from his total, instead of adding it.
C. Replace one of the 1-6 dice with a 4-9 die, or use two 4-9 dice instead. Players will multiply and add larger numbers.
D. Use the Challenge version of the Moolah on My Mind Record Sheet. Instead of adding the sum of the two dice, players choose whether to add, subtract or multiply the numbers. The winner is the player who finishes the game closest to $6.00.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 4 Answer Key
How Much Money?
Question 1.
Nadia has 2 nickels and 3 pennies. Taj has four times as much money as Nadia.
a. How much money does Taj have? Show your work using numbers, labeled sketches or words.
Answer:
Given,
Nadia has 2 nickels and 3 pennies.
Taj has four times as much money as Nadia.
Nadia = 2 + 3 = 5
5 × 4 = 20
Taj have 20
b. Fill in the bubble beside the equation that best represents this situation (m stands for Taj’s money).
![]() (2 + 3) × 4 = m
(2 + 3) × 4 = m
![]() (2 + 3) – 4 = m
(2 + 3) – 4 = m
![]() 4 × ((2 × 5) + (3 × 1)) = m
4 × ((2 × 5) + (3 × 1)) = m
Answer: (2 + 3) × 4 = m is the correct answer.
Question 2.
Zafar has 1 dime, 1 nickel, and 2 pennies. Petra has three times as much money as Zafar.
a. How much money does Petra have? Show your work using numbers, labeled sketches, or words.
Answer:
Given,
Zafar has 1 dime, 1 nickel, and 2 pennies.
1 dime = 10 cents
1 nickel = 5 cents
2 pennies = 1 cent
10 + 5 + 1 = 16 cents
Petra has three times as much money as Zafar.
16 × 3 = 48 cents
b. Write an equation to represent this problem.
Answer:
3(10 + 5 + 1) = 3 × 16 = 48 cents
Question 3.
CHALLENGE Sara has only nickels in her hand, and David has exactly the same number of dimes and no other coins. Together, they have a total of $1.05. How many nickels does Sara have? How many dimes does David have? Show your work using numbers, labeled sketches, or words.
Answer:
Let the number of nickels be x.
0.5x + 0.1x = $1.05
1 dollar = 10 dimes
1 dollar = 20 nickels
10.05 + 0.1x = 1.05
x = 7
Sara has 7 nickels
David has 7 dimes.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 3 Session 5 Answer Key
Money Multiple Wheel
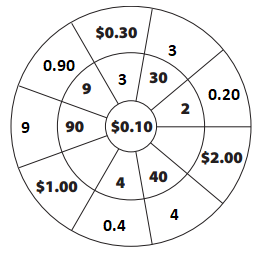
Question 1.
Fill in the Multiple Wheel.
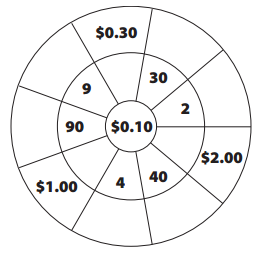
Answer:
0.10 × 3 = 0.30
0.10 × 9 = 0.90
0.10 × 90 = 9
0.10 × 4 = 0.4
0.40 × 40 = 4
2 ÷ 0.10 = 20
0.10 × 10 = 1
0.10 × 2 = 0.20
0.10 × 30 = 3
Question 2.
Fill in the blanks.
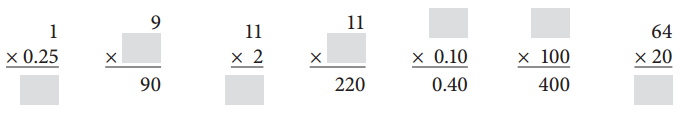
Answer:
1 × 0.25 = 0.25
9 × 10 = 90
11 × 2 = 22
11 × 20 = 220
4 × 0.10 = 0.40
4 × 100 = 40
64 × 20 = 1280
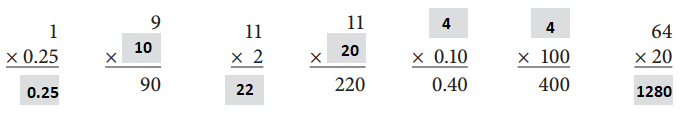
Question 3.
Fill in the bubble beside every item below that is not correct.
![]() 10 × 39 is 39 tens
10 × 39 is 39 tens
![]() 10 × 39 has to be less than 300 because 10 × 30 = 300
10 × 39 has to be less than 300 because 10 × 30 = 300
![]() 39 is prime
39 is prime
![]() 10 × 39 is 39 hundred
10 × 39 is 39 hundred
Answer:
10 × 39 = 390 = 39 tens
390 is greater than 300.
39 has more than 2 factors so it is not a prime number.
10 × 39 = 390 not equal to 39 hundred.
![]() 10 × 39 is 39 tens
10 × 39 is 39 tens
![]() 10 × 39 has to be less than 300 because 10 × 30 = 300
10 × 39 has to be less than 300 because 10 × 30 = 300
![]() 39 is prime
39 is prime
![]() 10 × 39 is 39 hundred
10 × 39 is 39 hundred
Question 4.
CHALLENGE Tera counted the coins in her bank and found 25 dimes, 12 quarters, and 15 nickels. If she saves twice as much next month, how much money will she have in all? Show your work.
Answer:
Given,
Tera counted the coins in her bank and found 25 dimes, 12 quarters, and 15 nickels.
25 × 2 = 50 dimes
12 × 2 = 24 quarters
15 × 2 = 30 nickels
25 + 50 = 75 dimes
12 + 24 = 36 quarters
30 + 15 = 45 nickels
Thus she saves 75 dimes, 36 quarters and 45 nickels in all.