Practicing the Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 6 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 6 Module 2
Bridges in Mathematics Grade 4 Home Connections Unit 6 Module 2 Session 2 Answer Key
Frankie’s Fairground
Frankie goes to the county fair every year. This year, she finds a math problem everywhere she goes. Help Frankie solve the problems. First make an estimate. Then write an equation with a letter standing for the unknown quantity. Finally, solve the problem. Show your work using numbers, labeled sketches, or words.
Question 1.
Frankie buys 24 tickets to use at the fair. Each ticket costs 25 cents. How much money does Frankie spend on tickets?
Estimate: _______________
Equation: _______________
Answer:
Estimate: 25 x 25 = 625 cents
Equation: X = 24 x 25
Explanation:
Frankie buys 24 tickets to use at the fair.
Each ticket costs 25 cents.
1 ticket = 25 cents
24 tickets = X
X = 25 x 24
X = 600 cents
Frankie spends 600 cents on tickets.
Question 2.
Frankie goes on the Ferris wheel first. The Ferris wheel stands on a rectangular platform that has an area of 324 yd2 (square yards). One dimension is 9 yards. What is the other dimension?
Estimate: _______________
Equation: _______________
Answer:
Estimate: 324/10 = 32.4 yards
Equation: 324 = 9 × X
Explanation:
The Ferris wheel stands on a rectangular platform that has an area of 324 yd2 (square yards).
One dimension is 9 yards.
Area = Width x height
324 yd2 = 9 yards × X
324 yd2/9yd = X
36 yards = X
The other dimension is 36 yards.
Question 3.
Next, Frankie goes on the Thrill Ride roller coaster. The roller coaster takes up a large rectangular area of the fairground. It is 99 yards on one side and 88 yards on the other side. How much space does the roller coaster take up in square yards?
Estimate: ________________
Equation: ________________
Answer:
Estimate: 100 x 90 = 9,000 square yards
Equation: X = 99 yards × 88 yards
Explanation:
The roller coaster takes up a large rectangular area of the fairground.
It is 99 yards on one side and 88 yards on the other side.
Area = length × width
Area = 99 × 88
Area = 8,712 square yards
The roller coaster takes up 8,712 square yards.
Question 4.
Write and solve an equation for each of the problems below. Use the table to help.
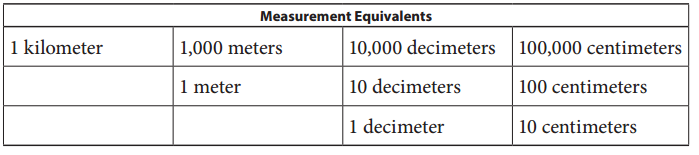
a. How many centimeters are in 45 meters?
Answer:
From the above given table, we know that,
1 meter = 100 centimeters
45 meters = X
X = 100 × 45
X = 450 centimeters
There are 450 centimeters in 45 meters.
b. How many meters are in 45 kilometers?
Answer:
From the above given table, we know that,
1 kilometer = 1000 meters
45 kilometers = X
X = 1000 × 45
X = 4,500 meters
There are 4,500 meters in 45 Kilometers.
c. How many meters are in 800 centimeters?
Answer:
From the above given table, we know that,
1 meter = 100 centimeters
X = 800 centimeters
100 × X = 800 × 1
100 X = 800
X = 800/100
X = 8 meters
There are 8 meters in 800 centimeters.
d. CHALLENGE How many decimeters are in 40 kilometers?
Answer:
From the above given table, we know that,
1 kilometer = 10,000 decimeters
40 kilometers = X
X = 10,000 × 40
X = 400,000 decimeters
There are 400,000 decimeters in 40 kilometers.
Bridges in Mathematics Grade 4 Home Connections Unit 6 Module 2 Session 4 Answer Key
Perimeter & Area
Use labeled sketches and equations to solve the problems on this page and the next. Show all your work.
Question 1.
Josie is putting a fence around her rectangular yard. One dimension measures 24 feet and the other dimension is twice as long. What is the perimeter of Josie’s yard?
Answer:
Josie is putting a fence around her rectangular yard.
One-dimension measures 24 feet.
The other dimension is twice as long.
24 x 2 = 48 feet
Perimeter of a rectangular yard = 2(24 + 48)
= 2(72)
= 144 feet
The perimeter of Josie’s yard is 144 feet.
Question 2.
If Josie puts grass in her yard, how many square feet of grass should she buy?
Answer:
Area = 24 × 48
= 1,152 square feet
Joise has to buy 1,152 square feet of grass.
Question 3.
Sean measured his rectangular patio and determined the area was 216 square feet. He remembered that one dimension was 9 feet.
a. What is the other dimension?
Answer:
Area of rectangular Patio is 216 square feet.
One dimension is 9 feet.
The other dimension = X
Area of rectangular Patio = 9 feet × X
216 Square feet = 9 feet × X
216/9 = X
24 feet = X
The other dimension is 24 feet.
b. What is the perimeter of Sean’s patio?
Answer:
Perimeter = 2(9 + 24)
= 2(33)
= 66 feet
Perimeter of Sean’s ratio is 66 feet.
Question 4.
Rafael and his sister each drew a rectangle on their driveway. The dimensions of Rafael’s rectangle are 16 inches and 24 inches. His sister’s rectangle has dimensions of 18 inches and 22 inches.
a. Whose rectangle has the larger area?
Answer:
The dimensions of Rafael’s rectangle are 16 inches and 24 inches.
Area of rectangle = 16 × 24
= 384 square inches
Area of Rafael’s rectangle is 384 square inches.
Rafael’s sister’s rectangle has dimensions of 18 inches and 22 inches.
Area of rectangle = 18 × 22
= 396 square inches
Area of Rafael’s sister rectangle is 396 square inches.
Rafael’s sister’s rectangle has larger area.
b. By how much?
Answer:
Area of Rafael’s rectangle is 384 square inches.
Area of Rafael’s sister rectangle is 396 square inches.
Subtract 384 from 396 the difference is 12 square inches.
396 – 384 = 12 square inches
c. Whose rectangle has a larger perimeter?
Answer:
Perimeter of Rafael’s rectangle = 2(16 + 24)
= 2(40)
= 80 inches
Perimeter of Rafael’s rectangle is 80 inches.
Perimeter of Rafael’s sister rectangle is = 2(18 + 22)
= 2(40)
= 80 inches
Perimeter of Rafael’s sister’s rectangle is 80 inches.
Both have equal perimeter.
Question 5.
CHALLENGE Daria and Luis both drew rectangles. Daria’s rectangle has an area of 180 inches and one of the dimensions is 12 inches. Luis’s rectangle has a perimeter of 48 inches with one dimension of 13 inches.
a. What is the perimeter of Daria’s rectangle?
Answer:
Daria’s rectangle has an area of 180 square inches.
One of the dimensions is 12 inches.
Take the other dimension as X.
Area of Daria’s rectangle = 12 × X
180 = 12 × X
180/12 = X
15 inches = X
The other dimension is 15 inches.
The perimeter of Daria’s rectangle = 2(12 + 15)
= 2(27)
= 54 inches
The perimeter of Daria’s rectangle is 54 inches.
b. What is the area of Luis’s rectangle?
Answer:
Luis’s rectangle has a perimeter of 48 inches.
One dimension is 13 inches.
Take the other dimension as X.
Perimeter = 2(13 + X)
48 inches = 2 × 13 + 2 × X
48 = 26 + 2X
48 – 26 = 2X
22 = 2X
X = 22/2
X = 11 inches
The other dimension is 11 inches.
The area of Luis’s rectangle = 13 x 11
= 143 square inches.
The area of Luis’s rectangle is 143 square inches.