Bridges in Mathematics Grade 4 Home Connections Unit 5 Module 1 Answer Key

Practicing the Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 5 Module 1 will help students analyze their level of preparation.

Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 5 Module 1

Bridges in Mathematics Grade 4 Home Connections Unit 5 Module 1 Session 2 Answer Key

Reviewing Area & Perimeter

Question 1.
Find the area and perimeter of each rectangle. Area is the total amount of space covered by the rectangle. Perimeter is the distance around the rectangle.
ex:

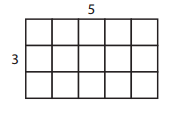
Perimeter: 3 + 3 + 5 + 5= 16 units
Area: 3 × 5 = 15 square units

a.

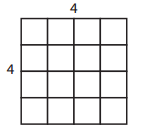
Perimeter: _______________
Area: _______________
Answer:
Given side of a square(side) = 4
Perimeter = 4 x side
= 4 x 4
= 16 units.
Area = Side²
= Side²
= 4²
= 4 x 4
=16 units

b.

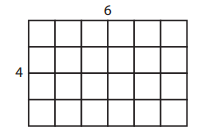
Perimeter: _______________
Area: _______________
Answer:
Given Length of a Rectangle (l) = 6 units
Width of a Rectangle (w) = 4 units
Perimeter = 2(l+w)
= 2( 6+4)
= 2(10)
= 20 units
Area = l.w
= 6. 4
= 24 units

c.

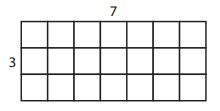
Perimeter: _______________
Area: _______________
Answer:
Given Length of a Rectangle (l) = 7  units
Width of a Rectangle (w) = 3 units
Perimeter = 2(l+w)
= 2( 7+3 )
= 2(10)
=20 units
Area = l.w
= 7.3
= 21 units

Question 2.
CHALLENGE Find the area and perimeter of this shape. Show all your work.

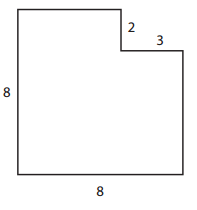
Perimeter: _______________
Area: _______________
Answer:

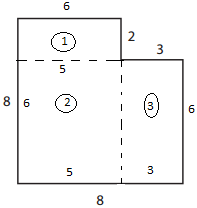
Area of first triangle =  l x b
= 2 x 5
= 10
Similarly
Area of second triangle =  l x b
= 6 x 5
= 30
Area of second triangle =  l x b
= 6 x 3
= 18
Total area of three triangles = 10 + 30+ 18
= 58
Perimeter of first triangle = 2(l+b)
= 2 (2+5)
= 2 x 7
= 14
Perimeter of second triangle = 2(l+b)
= 2 (6+5)
= 2 x 11
= 22
Perimeter of third triangle = 2(l+b)
= 2 (6+3)
= 2 x 9
= 18
Total perimeter of three triangles = 14+ 22 + 18
= 54
Question 3.
You can make sketches to help solve the problems below. Remember to include the units of measurement in your answers. Show all of your work.
a. The classroom rug is 9 feet long and 8 feet wide. What is the total area of the rug?
Answer:
Given Length of rug (l) = 9 feet long
Width of rug (w) = 8
Area of rug = length x width
= 9 x 8
= 72

b. What is the perimeter of the rug?
Answer:
Length of rug (l) = 9 feet long
Width of rug (w) = 8
Perimeter of rug = 2(l+w)
= 2(9 + 8)
= 2 (17)
= 34 units

Question 4.
Chrissy is going to make a big painting on a piece of wood that is 4 feet wide and 7 feet long. What is the total area of the piece of wood?
Answer:
Length of wood (l) = 7 feet
Width of wood (w) = 4 feet
Area of piece of wood = l. w
= 7 . 4
= 28 units.

a. What is the perimeter of the piece of wood?
Answer:
Length of wood (l) = 7 feet
Width of wood (w) = 4 feet
Perimeter of wood = 2 (l+w)
= 2(7+4)
= 2(11)
= 22 units.

Question 5.
The school playground measures 465 feet by 285 feet. What is the perimeter of the playground?
Answer:
Length of school playground = 465
Length of school playground = 285
perimeter of the playground = 2(l+w)
= 2(465+285)
= 2(750)
= 1500 units

Bridges in Mathematics Grade 4 Home Connections Unit 5 Module 1 Session 4 Answer Key

Angles & Rectangles

Question 1.
Alexis put two 90° angles together to make a new angle. How many degrees does the new angle measure?
a. 90° × 2 = ______________
Answer:
When Alexa places two 90° angles together to make a new angle , it is 180° degrees.
i.e. 90°  x 2 = 180°

b. What kind of angle did Alexis make? Fill in the bubble to show.
acute angle (less than 90°)
right angle (exactly 90°)
obtuse angle (more than 90° but less than 180°)
straight angle (exactly 180°)
Answer:
Straight angle (excatly 180°)

Question 2.
Henry put three 45° angles together to make a new angle. How many degrees does the new angle measure?
a. 45° × 3 = ________________
Answer:
When Henry places three 45° angles together to make a new angle , it is 135° degrees.
i.e. 45 ° x 3 = 135°

b. What kind of angle did Henry make? Fill in the bubble to show.
acute angle
right angle
obtuse angle
straight angle
Answer:
Henry makes the kind of angle called obtuse angle which lies in between the 90°  and 180° .

Question 3.
Austin put four 15° angles together to make a new angle. How many degrees does the new angle measure?
a. 15° × 4 = _______________
Answer:
When Austin put four 15° angles together for making a new angle , it is 60° degrees.

b. What kind of angle did Austin make? Fill in the bubble to show.
acute angle
right angle
obtuse angle
straight angle
Answer:
Since Austin makes makes the angle below 90°  , it is an acute angle.

Question 4.
Claudia drew and labeled a rectangle. Here is a miniature picture of her rectangle. Use this picture to help answer the questions below.

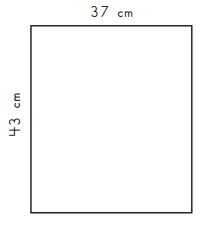
a. What is the sum of the 4 interior angles in Claudia’s rectangle? Show your work.
Answer:
sum of interior agles in a claudia’s rectagle  = 180°  x(n-2)
where n is numer of sides n = 4
= 180°  x (4-2)
= 180°  x 2
= 360°

b. What is the perimeter of Claudia’s rectangle? Show your work.
Answer:
Given legth of rectagle (l) = 37 cm
Width of rectangle(W) = 43 cm
perimeter  = 2(l +W)
= 2(37+43)
= 160 cm

c. What is the area of Claudia’s rectangle? Show your work.
Answer:
Given legth of rectagle (l) = 37 cm
Width of rectangle(W) = 43 cm
Area = l x w
= 37 x 43
= 1591 cm

Question 5.
CHALLENGE Claudia colored half of her rectangle blue. What is the area of the blue part of the rectangle? Show your work.
Answer:
Actual area of Rectangle obtained = 1591 cm
When half of rectangle is colored with blue = 1591 / 2
= 795.5 cm

Bridges in Mathematics Grade 4 Home Connections Unit 5 Module 1 Session 6 Answer Key

Protractor Practice

When you measure an angle you usually have to choose between two numbers because protractors are designed to measure angles that start on either the right or left side. There are two angles to measure in each of the problems on this sheet and the next. The angle on the left side is angle A. The angle on the right side is angle B. Find and record the measure of both angles in each problem.

Question 1.
The measure of angle A is _____________ degrees.
The measure of angle B is ______________ degrees.

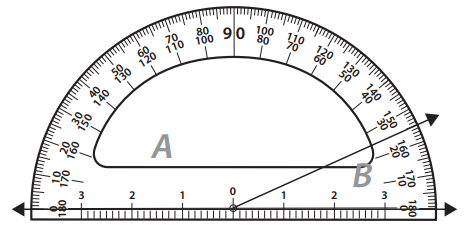
Answer:
From the Given diagram the value of ∠B = 155°. To know the value of ∠A subtract ∠B value from 180° .
∠A =  180° – 155°
∠A = 25°

Question 2.
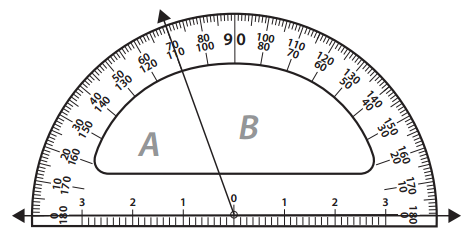
The measure of angle A is _____________ degrees.
The measure of angle B is _____________ degrees.

Answer:
From the Given diagram the value of ∠B = 70°. To know the value of ∠A subtract ∠B value from 180° .
∠A =  180° – 70°
∠A = 110°

Question 3.
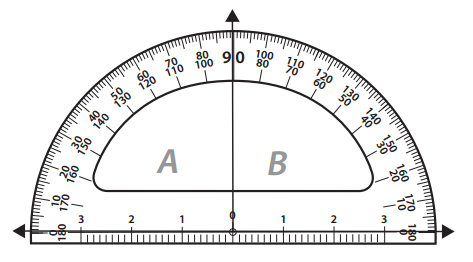
The measure of angle A is _____________ degrees.
The measure of angle B is _____________ degrees.

Answer:
From the Given diagram the value of ∠B = 90°. To know the value of ∠A subtract ∠B value from 180° .
∠A =  180° – 90°
∠A = 90 °

Question 4.
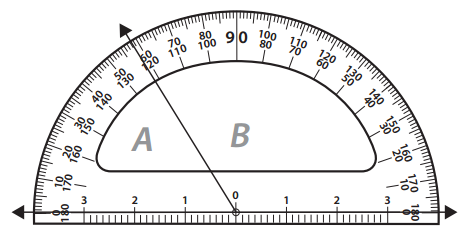
The measure of angle A is _____________ degrees.
The measure of angle B is _____________ degrees.

Answer:
From the Given diagram the value of ∠B = 122°. To know the value of ∠A subtract ∠B value from 180° .
∠A =  180° – 122°
∠A = 58°

Question 5.
Go back and add each pair of angle measures in Problems 1 through 4. What do you notice? Why do you think it works this way?
Answer:
problem 1 values: A = 155,  B = 25 : Sum = 155 + 25 = 180°
problem 2 values: A = 110,  B = 70 : Sum = 155 + 25 = 180°
problem 3 values: A = 90,  B = 90  : Sum = 155 + 25 = 180°
problem 4 values: A = 58,  B = 122 : Sum = 155 + 25 = 180°
I noticed, When both values in 4 problems are added , the result obtained is 180 degrees each.