The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 8 Module 4 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 8 Module 4
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 4 Session 1 Answer Key
Lemonade Stand
Philipe is making lemonade to serve at a lemonade stand. His recipe makes 6 glasses of lemonade. The recipe calls for 4 lemons, 1 cup of sugar, and 6 cups of water. For Friday at the lemonade stand, Philipe wants to make enough lemonade to serve 1 glass each to 30 customers.
Question 1.
How many lemons does he need? Use words, numbers, or pictures to show your work.
Answer:
Number of lemons needed to serve for Friday at the lemonade stand = 120.
Explanation:
Number of glasses of lemonade his recipe makes = 6.
Number of lemons he recipe calls = 4.
Number of cup of sugar the recipe calls = 1.
Number of cups of water the recipe calls = 6.
Number of customers he wants to serve for Friday at the lemonade stand = 30.
Number of lemons needed to serve for Friday at the lemonade stand = Number of lemons he recipe calls × Number of customers he wants to serve for Friday at the lemonade stand
= 4 × 30
= 120.
Question 2.
When Philipe makes the lemonade, he gets 1 cup of lemon juice out of every 4 lemons. How many cups of liquid (lemon juice and water together) will be in his whole batch of lemonade?
Answer:
Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade = 330.
Explanation:
Number of glasses of lemonade his recipe makes = 6.
Number of lemons he recipe calls = 4.
Number of cup of sugar the recipe calls = 1.
Number of cups of water the recipe calls = 6.
Number of customers he wants to serve for Friday at the lemonade stand = 30.
Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade = (Number of lemons he recipe calls × Number of customers he wants to serve for Friday at the lemonade stand) + (Number of cup of sugar the recipe calls × Number of customers he wants to serve for Friday at the lemonade stand) + (Number of cups of water the recipe calls × Number of customers he wants to serve for Friday at the lemonade stand)
= (4 × 30) + (1 × 30) + (6 × 30)
= 120 + 30 + 180
= 150 + 180
= 330.
Question 3.
CHALLENGE Philipe expects to have more customers on Saturday since more people will be playing outside. He thinks he might serve as many glasses of lemonade as he did Friday, plus half again that many. How many recipes of lemonade should he make for Saturday? Use words, numbers, or pictures to explain your reasoning.

Answer:
Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade on Saturday = 495.
Explanation:
Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade = 330.
He thinks he might serve as many glasses of lemonade as he did Friday, plus half again that many.
=> Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade on Saturday = Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade + (Number of cups of liquid (lemon juice and water together) will be in his whole batch of lemonade ÷ 2)
= 330 + (330 ÷ 2)
= 330 + 165
= 495.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 4 Session 2 Answer Key
How Much Water?
Question 1.
One team in Mr. Frisbie’s class said the load limit of their bridge was 800 liters. Another team says it was 800 milliliters. Who is correct? Why? Explain your answer using numbers, pictures, or words.
Answer:
First team is correct because the load limit of their bridge was 800 liters not 800 milliliters.
Explanation:
Number of liters of one team in Mr. Frisbie’s class said the load limit of their bridge = 800.
Number of milliters another team says it was = 800.
Conversion:
1 liter = 1000 millilters.
800 liters = ????
=> 1 × ??? = 1000 × 800
=> ??? = 8,00,000 milliliters.
Question 2.
Another team is measuring the water the whole class will need for the load-limit tests. There are 10 teams in the class, and each team will need at least 1 water bottle full of water. Should they measure out 5 milliliters, 5 liters, 50 liters, or 500 liters of water? Why? Explain your answer using numbers, pictures, or words.
Answer:
500 liters of water should be measured because water bottle quantity is going to be in liters not milliliters.
Explanation:
Number of teams in the class = 10.
Number of bottle full of water each team will need = 1.
Total quantity of bottle full of water all teams needed = Number of teams in the class × Number of bottle full of water each team will need
= 10 × 1
= 10.
If, one water bottle is 1 liter:
Conversion:
1 liter = 1000 millilters.
5 milliliters = 5 × 1000 = 5000 milliliters.
5 liters = 5 water bottles.
50 liters = 50 water bottles.
500 liters = 500 water bottles.
Question 3.
A third team has already built an early version of their bridge design and is measuring its load limit. They hung a bottle containing 65 milliliters from the bridge, then hung another bottle from that one. At first, the second bottle held 50 milliliters, but the bridge still held it, so they added more water to it. Their bridge held 145 milliliters of water before collapsing. How much water was in the second bottle when the bridge collapsed? Show your work.
Answer:
Number of water was in the second bottle when the bridge collapsed = 80.
Explanation:
Number of milliliters of bottle they hung from the bridge = 65.
Number of milliliters at first, the second bottle held = 50.
Number of milliliters of water their bridge held before collapsing = 145.
Number of water was in the second bottle when the bridge collapsed = Number of milliliters of water their bridge held before collapsing – Number of milliliters of bottle they hung from the bridge
= 145 – 65
= 80.
Question 4.
Solve the problems.
3 × ___________ = 36
___________ ÷ 4 = 9
36 = ___________ × 2
__________ = 3 × (5 + 7)
(2 + 8) × 10 = ____________
___________ = 4 × (4 + 5)
___________ = 4 × 10 × 2
6 × (3 + 3) = ___________
Answer:
3 × _____12______ = 36.
____36_______ ÷ 4 = 9.
36 = ___18________ × 2.
____48______ = 3 × (5 + 7).
(2 + 8) × 10 = ____100________.
_____36______ = 4 × (4 + 5).
___80________ = 4 × 10 × 2.
6 × (3 + 3) = _____36______.
Explanation:
Given Equations:
3 × ?? = 36.
=> ?? = 36 ÷ 3
=> ?? = 12.
?? ÷ 4 = 9.
=> ?? = 9 × 4
=> ?? = 36.
36 = ?? × 2.
=> 36 ÷ 2 = ??
=> 18 = ??.
?? = 3 × (5 + 7)
=> ?? = 3 × 12
=> ?? = 48.
(2 + 8) × 10 = ??.
=> 10 × 10 = ??
=> 100 = ??.
?? = 4 × (4 + 5)
=> ?? = 4 × 9
=> ?? = 36.
?? = 4 × 10 × 2
=> ?? = 40 × 2
=> ?? = 80.
6 × (3 + 3) = ??.
=> 6 × 6 = ??
=> 36 = ??.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 4 Session 3 Answer Key
More Bridge Patterns
Question 1.
Cassandra built some truss bridges using trapezoids for the trusses. She made sketches of her bridges like those shown below.

How many toothpicks will it take to build a truss bridge with 8 trapezoids? Explain your answer using labeled sketches, numbers, and words.
Answer:
33 toothpicks it takes to build a truss bridge with 8 trapezoids because from 1 to 2 trapezoids building 4 more toothpicks are added same till 8 trapezoids building.
Explanation:
Number of toothpicks 1-Trapezoid Truss made = 5.
Number of toothpicks 2-Trapezoid Truss made = 9.
Number of toothpicks 3-Trapezoid Truss made = 13.
Number of toothpicks 4-Trapezoid Truss made = 17.
Number of toothpicks 5-Trapezoid Truss made = 21.
Number of toothpicks 6-Trapezoid Truss made = 25.
Number of toothpicks 7-Trapezoid Truss made = 29.
Number of toothpicks 8-Trapezoid Truss made = 33.
Question 2.
Cassandra wanted to make her truss bridges stronger, so she added toothpicks to turn the trapezoids into triangles.
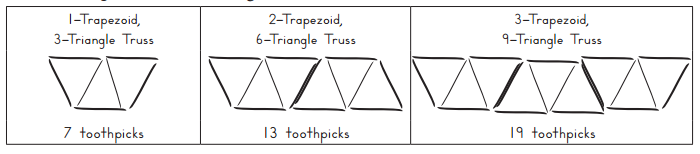
a. Fill in the table to show the new relationships of toothpicks to trusses.

Answer:

Explanation:
Difference:
Triangles = 6 – 3 = 3.
Number of toothpicks = 13 – 7 = 6.
Trapezoids Triangles Number of Toothpicks
1 3 7
2 6 13
3 9 19
4 12 25
5 15 31
6 18 37
7 21 43
8 24 49
b. How many triangles will it take to build a truss bridge with 10 trapezoids?
Answer:
30 triangles it takes to build a truss bridge with 10 trapezoids.
Explanation:
Trapezoids Triangles Number of Toothpicks
1 3 7
2 6 13
3 9 19
4 12 25
5 15 31
6 18 37
7 21 43
8 24 49
9 27 55
10 30 61
c. How many toothpicks will Cassandra need to build the bridge with 10 trapezoids?
Answer:
61 toothpicks Cassandra needs to build the bridge with 10 trapezoids.
Explanation:
Trapezoids Triangles Number of Toothpicks
1 3 7
2 6 13
3 9 19
4 12 25
5 15 31
6 18 37
7 21 43
8 24 49
9 27 55
10 30 61
Question 3.
Solve the problems below.
6 × 9 = ____________
8 × (5 + 3) = _______________
(5 + __________) × 9 = 54
(8 × 5) + (___________ × 3) = 64
Answer:
Equations:
6 × 9 = _____54_______.
8 × (5 + 3) = ______64_________.
(5 + _____1_____) × 9 = 54
(8 × 5) + (_____8______ × 3) = 64
Explanation:
Given Equations:
6 × 9 = ??
=> 6 × 9 = 54.
8 × (5 + 3) = ??
=> 8 × 8 = ??
=> 64 = ??
(5 + ??) × 9 = 54.
=> (5 + ??) = 54 ÷ 9
=> (5 + ??) = 6
=> ?? = 6 – 5
=> ?? = 1.
(8 × 5) + (?? × 3) = 64.
=> 40 + (?? × 3) = 64.
=> (?? × 3) = 64 – 40
=> (?? × 3) = 24
=> ?? = 24 ÷ 3
=> ?? = 8.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 4 Session 4 Answer Key
Graphing the Final Bridges
How Much Time?
Question 1.
Mr. Frisbie’s class has 1 hour and 10 minutes to work on their bridges.
- They need 5 minutes to gather materials.
- It will take them twice as long to clean up.
- They want to spend 30 minutes building and testing their bridges.
- They need the remaining time to draw a picture of the bridge.
How many minutes can they spend on each task? Show your work below.
Answer:
Number of minutes needed to gather materials = 5.
Number of minutes in cleaning = 5.
Number of minutes they want to spend building and testing their bridges = 30.
Number of minutes to draw the bridge = 50.
Explanation:
Time of Mr. Frisbie’s class has to work on their bridges = 1 hour and 10 minutes.
Number of minutes needed to gather materials = 5.
Number of times it takes them to clean up = 2.
Number of minutes they want to spend building and testing their bridges = 30.
Time they need the remaining time to draw a picture of the bridge = ??
Total time they do the activity = (Number of minutes needed to gather materials × Number of times it takes them to clean up) + Number of minutes they want to spend building and testing their bridges + Time they need the remaining time to draw a picture of the bridge
= 1 hr 30 minutes = (5 × 2) + 30 + ??
=> 60 minutes + 30 minutes = 10 + 30 + ??
=> 90 = 40 + ??
=> 90 – 40 = ??
=> 50 minutes = ??
Question 2.
Ms. Delawney’s class has 25 minutes to prepare for a bridge design showcase. They’ll start their preparations at 2:15 p.m.
- They will first use 10 minutes to write statements explaining their designs.
- Next, they will spend half as long making covers for their folders.
- Last, they will use the remaining time to plan activities and games for the showcase.
At what time will they need to start each task? Show your work below.
Answer:
Time they start the they need to start each task = 2.25 pm.
Explanation:
Number of minutes Ms. Delawney’s class has to prepare for a bridge design showcase = 25.
Time they start their preparations at = 2:15 p.m.
Number of minutes they use to write statements explaining their designs = 10.
Number of minutes they will spend half as long making covers for their folders = 25 – 10 = 12.50.
Number of minutes they will use the remaining time to plan activities and games for the showcase = ??
Number of minutes Ms. Delawney’s class has to prepare for a bridge design showcase = Number of minutes they use to write statements explaining their designs + 12.50 + ??
=> 25 = 10 + 12.50 + ??
=> 25 = 22.50 + ??
=> 25 – 22.50 = ??
=> 2.50 minutes = ??
Time they start the they need to start each task = 2.15 + 10 = 2.25 pm.