The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 8 Module 3 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 8 Module 3
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 1 Answer Key
How Much Time Does He Need?
Question 1.
Joshua has one hour to work on his race car today.
- He needs 5 minutes to set up tools.
- It will take him twice as long to clean up as it takes to set up the tools.
- He wants to spend half his time working on building his car.
- He needs the remaining time to make drawings of his building plans.
a. How many minutes can he spend on each task? Show your work.
- Set up tools ________________
- Make drawings of building plans ________________
- Work on building the car ________________
- Clean up tools ________________
Answer:
Number of minutes he spends on each task:
- Set up tools ______5__________.
- Make drawings of building plans ____22.50____________.
- Work on building the car ______22.50__________.
- Clean up tools _______10_________.
Explanation:
Total time he has to work on his race car today = 1.
Number of minutes to set up tools = 5.
It will take him twice as long to clean up as it takes to set up the tools.
=> Number of minutes to clean = 5 × 2 = 10.
He wants to spend half his time working on building his car.
=> Number of minutes working on building his car = (Total time he has to work on his race car today – 10 – 5) ÷ 2
= (60 – 15) ÷ 2
= 45 ÷ 2
= 22.50.
He needs the remaining time to make drawings of his building plans.
=> Number of minutes the remaining time to make drawings of his building plans = (60 – 22.50 – 10 – 5)
= 60 – 37.50
= 22.50.
b. If he begins at 4:35 in the afternoon, at what time should he begin each task?
- Set up tools ________________
- Make drawings of building plans ________________
- Work on building the car ________________
- Clean up tools ________________
Answer:
Time he begins each task:
Set up tools _______4:40 PM_________.
Make drawings of building plans _____5:00 PM___________.
Work on building the car ______5:22 PM__________.
Clean up tools ______5:32 PM__________.
Explanation:
Time he begins setting up tools = 4:35 PM.
Total time he has to work on his race car today = 1.
Number of minutes to set up tools = 5.
=> Time he starts setting up tools = 4.40 Pm.
Number of minutes working on building his car = 22.50.
=> Time he starts working on building his car = 4.40 + 22.50 minutes = 5:00 PM.
Number of minutes the remaining time to make drawings of his building plans = 22.50
=> Time he starts to make drawings of his building plans = 5:00 PM + 22.50 minutes = 5:22 PM.
Number of minutes to clean = 10.
=> Time to clean = 5:22 PM + 10 minutes = 5:32 PM.
Question 2.
Solve the problems below.
60 ÷ __________ = 15
3 × 20 = _____________
___________ ÷ 5 = 12
15 × ______________ = 120
Answer:
Equations:
60 ÷ ____4______ = 15.
3 × 20 = _____60________.
____60_______ ÷ 5 = 12.
15 × ______8________ = 120.
Explanation:
Given equations:
60 ÷ ?? = 15.
=> 60 ÷ 15 = ??
=> 4 = ??
3 × 20 = ??.
=> 3 × 20 = 60.
?? ÷ 5 = 12.
=> ?? = 12 × 5
=> ?? = 60.
15 × ?? = 120.
=> ?? = 120 ÷ 15
=> ?? = 8.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 2 Answer Key
The Class Party
The students in Mr. Frisbie’s class are having a party today. Answer the questions about the party activities.
Question 1.
School ends at 3:00, and the party starts 1 hour and 15 minutes before the end of school. What time does the party start?
Answer:
Time at party starts = 1:45.
Explanation:
Time school ends at = 3:00.
Time party starts before the end of school = 1 hour and 15 minutes.
Time at party starts = Time school ends at – Time party starts before the end of school
= 3:00 – 1:15
= 1:45.
Question 2.
As soon as the party starts, the students need 5 minutes to pass out the party treats. What time will it be when everyone has their treats?
Answer:
Time everyone has their treats = 1:50.
Explanation:
Time at party starts = 1:45.
As soon as the party starts, the students need 5 minutes to pass out the party treats.
=> Time everyone has their treats = Time at party starts + 5 minutes
= 1:45 + 0.05
= 1:50.
Question 3.
The class is going to enjoy their treats for 20 minutes and then go outside to play games. What time will they go outside?
Answer:
Time when they go outside = 2:10.
Explanation:
Time everyone has their treats = 1:50.
The class is going to enjoy their treats for 20 minutes and then go outside to play games.
=> Time when they go outside = Time everyone has their treats + 20 minutes
= 1:50 + 0.20
= 2:10.
Question 4.
They get to play games outside for 30 minutes. Then it’s time to return to the classroom. What time will they return to the classroom?
Answer:
Time they return to the classroom = 2:40.
Explanation:
Time when they go outside = 2:10.
They get to play games outside for 30 minutes.
=> Time they return to the classroom = Time when they go outside + 30 minutes
= 2:10 + 0.30
= 2:40.
Question 5.
When students return to the classroom, they’ll sing the song they’ve been practicing in music this year for Mr. Frisbie. The song is 4 minutes long, and they need 2 minutes before they start to get everyone ready. What time will it be when they’re done singing?
Answer:
Time when ther are done singing = 2:46.
Explanation:
Time they return to the classroom = 2:40.
The song is 4 minutes long, and they need 2 minutes before they start to get everyone ready.
Time when ther are done singing = Time they return to the classroom + 4 minutes + 2 minutes
= 2:40 + 0.04 + 0.02
= 2:44 + 0.02
= 2:46.
Question 6.
After singing, the class will clean up and get ready to go home. How much time do they have to do this before school is over?
Answer:
Time they have to do cleaning before school is over = 0.14 or 14 minutes.
Explanation:
Time when ther are done singing = 2:46.
Time school ends = 3:00.
Time they have to do cleaning before school is over = Time school ends – Time when ther are done singing
= 3:00 – 2:46
= 0.14 or 14 minutes.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 3 Answer Key
Strength Graph
Title _______________
Graphing Shapes in Our Bridges
One team in Mr. Carson’s class counted the shapes they found in their bridge and entered the data in the table below.
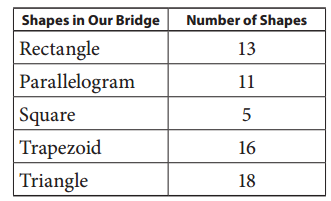
Question 1.
Draw the number of shapes the team found in their bridge in the picture graph below. Make each shape you draw represent 4 shapes. The rectangle data has been entered as an example.
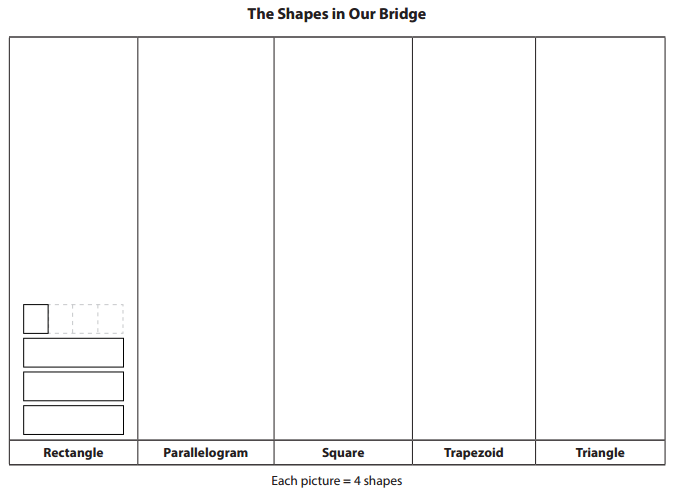
Answer:
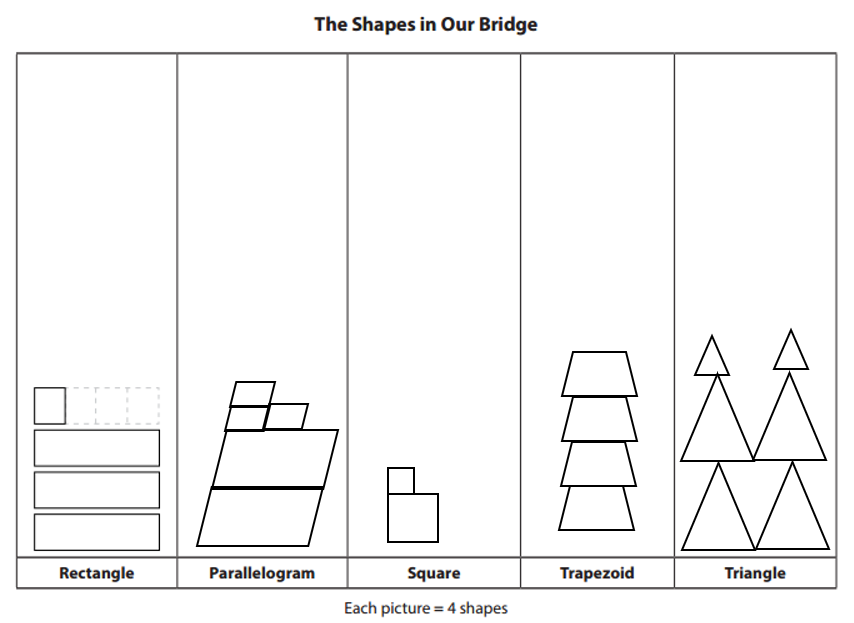
Explanation:
Given:
Each picture = 4 shapes.
Number of shapes rectangle bridge has = 13.
Number of shapes parallelogram bridge has = 11.
Number of shapes square bridge has = 5.
Number of shapes trapezoid bridge has = 16.
Number of shapes triangle bridge has = 18.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 4 Answer Key
Quadrilaterals & Perimeters
Question 1.
Label each figure below with its name and perimeter.

Answer:
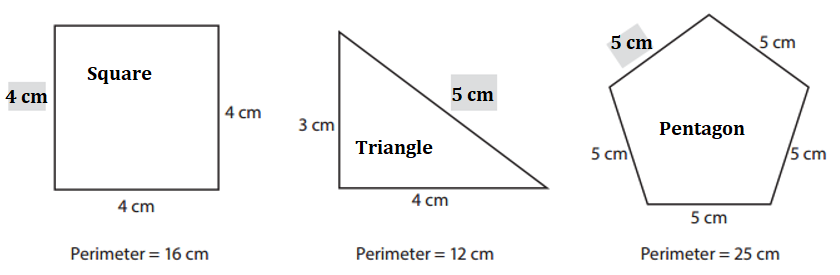
Explanation:
Length of the Sides of the figure = 4 cm each.
Perimeter of the figure = 16 cm.
=> Figure = Square.
Length of the figure = 4 cm.
Height of the figure = 3 cm.
Perimeter of the figure = 12 cm.
=> Figure = Triangle.
Length of the Sides of the figure = 5 cm each.
Perimeter of the figure = 25 cm.
=> Figure = Pentagon.
Question 2.
Label each figure below with its name and perimeter.
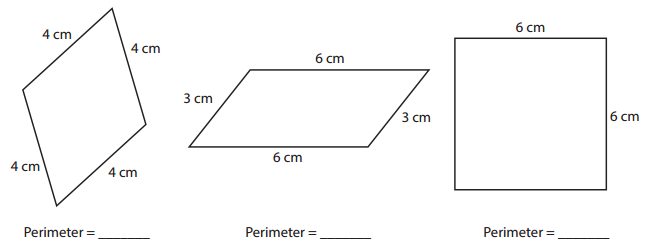
Answer:
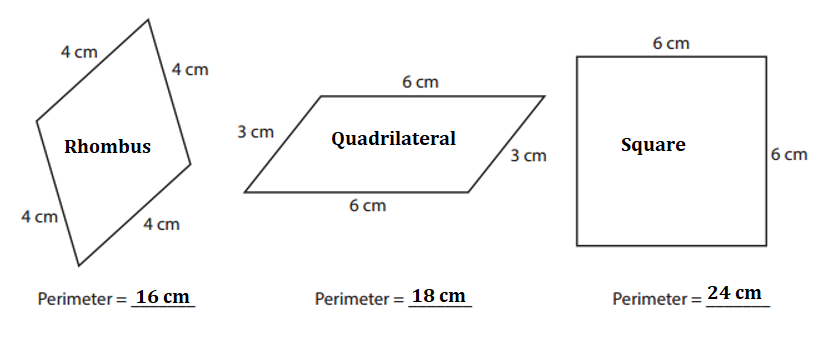
Explanation:
Length of the figure rhombus = 4 cm each.
Perimeter of rhombus = 4 × Length of the side
= 4 × 4
= 16 cm.
Length of the quadrilateral = 6cm.
Breadth of the quadrilateral = 3 cm.
Perimeter of the quadrilateral = 2 × (Length of the quadrilateral + Breadth of the quadrilateral)
= 2 × (6 + 3)
= 2 × 9
= 18 cm.
Length of the square = 6 cm each.
Perimeter of the square = 4 × Length of the square
= 4 × 6
= 24 cm.
Question 3.
Label each figure below with its name and area.
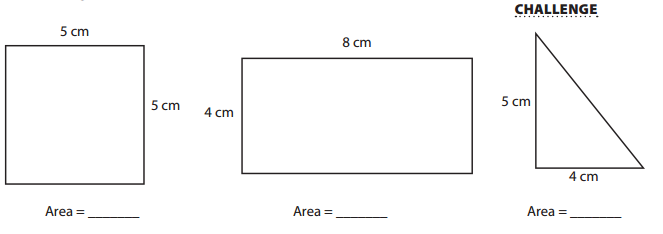
Answer:
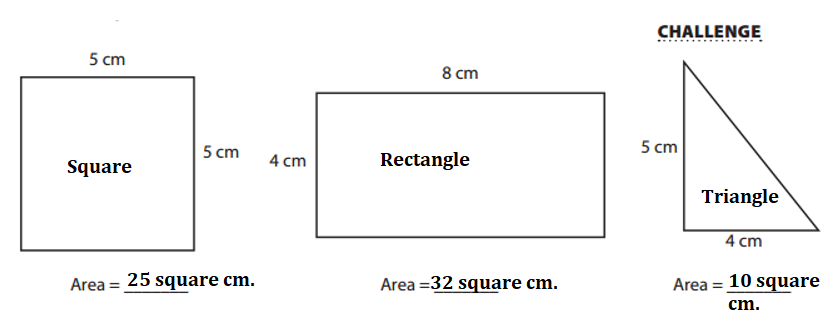
Explanation:
Length of the square = 5 cm each.
Area of the square = Length of the square × Length of the square
= 5 × 5
= 25 square cm.
Length of the rectangle = 8 cm.
Breadth of the rectangle = 4 cm.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 8 × 4
= 32 square cm.
Length of the triangle = 5 cm.
Height of the triangle = 4 cm.
Area of the triangle = (Length of the triangle × Height of the triangle) ÷ 2
= (5 × 4) ÷ 2
= 20 ÷ 2
= 10 square cm.
Question 4.
Draw a quadrilateral that has a different name than any of those shown above, and label it with its name.
Answer:
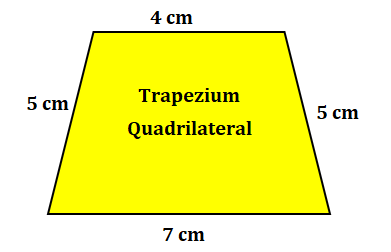
Explanation:
Quadrilateral with different label = ??
=>Trapezium is one other name of quadrilateral.
Measurements of trapezium = 7cm, 5 cm, 4 cm, 5 cm.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 5 Answer Key
Plot the Data
Question 1.
The students in Mr. Frisbie’s class measured their bridges’ deck thickness. The measurements are below:
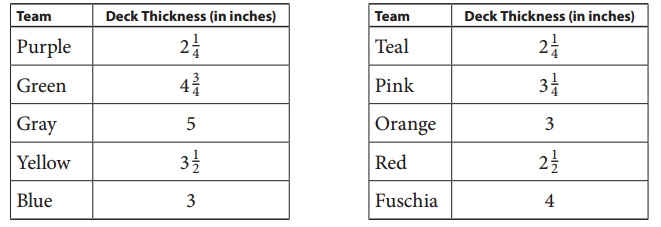
a. Draw a line plot to represent the class data. Remember to give the line plot a title and labels.
Title: _____________

Answer:
Explanation:
Given measurements:

b. What do you notice about the data? Write at least two observations.
Answer:
Two observation about the given data:
1. Team thinkness at starting was thickner than last.
2. The team thickness is becoming more lighter as per number of teams increased.
Explanation:
According to the given data,
1. Team thinkness at starting was thickner than last.
2. The team thickness is becoming more lighter as per number of teams increased.
Question 2.
Write <, =, or > to compare each pair of mixed numbers.
2\(\frac{1}{2}\) _______________ 2\(\frac{1}{4}\)
3\(\frac{1}{3}\) _______________ 3\(\frac{1}{4}\)
5\(\frac{2}{8}\) _______________ 5\(\frac{2}{3}\)
1\(\frac{4}{6}\) ________________ 1\(\frac{2}{3}\)
Answer:
2\(\frac{1}{2}\) > 2\(\frac{1}{4}\).
3\(\frac{1}{3}\) > 3\(\frac{1}{4}\).
5\(\frac{2}{8}\) < 5\(\frac{2}{3}\).
1\(\frac{4}{6}\) = 1\(\frac{2}{3}\).
Explanation:
2\(\frac{1}{2}\) _______________ 2\(\frac{1}{4}\)
=> {[(2 × 2) + 1] ÷ 2} _______________ {[(2 × 4) + 1] ÷ 4}
=> [(4 + 1) ÷ 2] _______________ [(8 + 1) ÷ 4]
=> 5 ÷ 2 _______________ 9 ÷ 4
=> 2.5 is greater than 2.25.
3\(\frac{1}{3}\) _______________ 3\(\frac{1}{4}\)
=> {[(3 × 3) + 1] ÷ 3} _______________ {[(3 × 4) + 1] ÷ 4}
=> [(9 + 1) ÷ 3] _______________ [(12 + 1) ÷ 4]
=> 10 ÷ 3 _______________ 13 ÷ 4
=> 3.33 is greater than 3.25.
5\(\frac{2}{8}\) _______________ 5\(\frac{2}{3}\)
=> {[(5 × 8) + 2] ÷ 8} _______________ {[(5 × 3) + 2] ÷ 3}
=> [(40 + 2) ÷ 8] _______________ [(15 + 2) ÷ 3]
=> 42 ÷ 8 _______________ 17 ÷ 3
=> 5.25 is lesser than 5.67.
1\(\frac{4}{6}\) ________________ 1\(\frac{2}{3}\)
=> {[(1 × 6) + 4] ÷ 6} _______________ {[(1 × 3) + 2] ÷ 3}
=> [(6 + 4) ÷ 6] _______________ [(3 + 2) ÷ 3]
=> 10 ÷ 6 _______________ 5 ÷ 3
=> 1.67 is equal to 1.67.
Bridges in Mathematics Grade 3 Student Book Unit 8 Module 3 Session 6 Answer Key
Considering Our Data
Question 1.
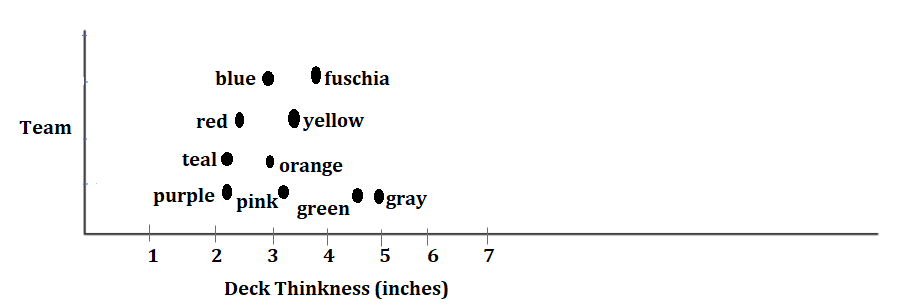
How many of each type of bridge is represented on the scatter plot?
Arch bridge:
Beam bridge:
Suspension bridge:
Answer:
Arch bridge: Purple, Teal, Red.
Beam bridge: Yellow, Orange, Pink, Blue.
Suspension bridge: Green, Gray, Fuschia.
Explanation:
Deck measurement- below 3 inches – Arch bridge.
Arch bridge: Purple, Teal, Red.
Deck measurement- 3 to 4 inches – Beam bridge.
Beam bridge: Yellow, Orange, Pink, Blue.
Deck measurement- 4 to 5 inches – Suspension bridge.
Suspension bridge: Green, Gray, Fuschia.

Question 2.
Calculate the mean, or average, deck width of each bridge type.
Arch bridge:
Beam bridge:
Suspension bridge:
Answer:
Mean of:
Arch bridge: 2.33 inches.
Beam bridge: 3.1875 inches
Suspension bridge: 4.583 inches.
Explanation:
Arch bridge: Purple, Teal, Red.
Mean = (2\(\frac{1}{4}\) +2\(\frac{1}{4}\) + 2\(\frac{1}{2}\)) ÷ 3
= 7 ÷ 3
= 2.33 inches.
Beam bridge: Yellow, Orange, Pink, Blue.
Mean = (3\(\frac{1}{2}\) + 3 + 3\(\frac{1}{4}\) + 3) ÷ 4
= 12\(\frac{3}{4}\) ÷ 4
= 3.1875 inches
Suspension bridge: Green, Gray, Fuschia.
Mean = (4\(\frac{3}{4}\) + 5 + 4) ÷ 3
= 13\(\frac{3}{4}\) ÷ 3
= 4.583 inches.
Mean = Total ÷ Number of items
= (2\(\frac{1}{4}\) + 4\(\frac{3}{4}\) + 5 + 3\(\frac{1}{2}\) + 3 + 2\(\frac{1}{4}\) + 3\(\frac{1}{4}\) +3 + 2\(\frac{1}{2}\) + 4) ÷ 10
= (31 + 2\(\frac{1}{2}\)) ÷ 10
= 33\(\frac{1}{2}\) ÷ 10
= 3.35 inches.
Question 3.
Was your bridge thicker or thinner than the average for its type? Write an expression using >, =, or < to show how your bridge’s deck thickness compares to the average.
Answer:
Arch bridge is thicker than the average for its type.
Beam bridge is thinner than the average for its type.
Suspension bridge is thicker than the average for its type.
Explanation:
Mean of:
Arch bridge: 2.33 inches is more than its type.
Beam bridge: 3.1875 inches is equal than its type.
Suspension bridge: 4.583 inches is more than its type.
Question 4.
Fill in the blanks.
a. The bridge with the thinnest deck had a span of ______________ inches.
Answer:
The bridge with the thinnest deck had a span of ______2.33_________ inches.
Explanation:
The bridge with the thinnest deck had a span of ?? inches.
Mean of:
Arch bridge: 2.33 inches is more than its type.
Beam bridge: 3.1875 inches is equal than its type.
Suspension bridge: 4.583 inches is more than its type.
b. The longest bridge’s deck was _______________ inches thick.
Answer:
The longest bridge’s deck was _____4.583__________ inches thick.
Explanation:
The longest bridge’s deck was ________??_______ inches thick.

Mean of:
Arch bridge: 2.33 inches is more than its type.
Beam bridge: 3.1875 inches is equal than its type.
Suspension bridge: 4.583 inches is more than its type.
c. The longest bridge was a(n) _______________ type of bridge.
Answer:
The longest bridge was a(n) _____gray(Suspension )__________ type of bridge.
Explanation:

Mean of:
Arch bridge: 2.33 inches is more than its type.
Beam bridge: 3.1875 inches is equal than its type.
Suspension bridge: 4.583 inches is more than its type.
d. The bridge with the thinnest deck was a(n) _______________ type of bridge.
Answer:
The bridge with the thinnest deck was a(n) ____Arch ___________ type of bridge.
Explanation:
Mean of:
Arch bridge: 2.33 inches is more than its type.
Beam bridge: 3.1875 inches is equal than its type.
Suspension bridge: 4.583 inches is more than its type.

The Javelin Throw
Sam and Tanisha are playing a new Measurement Olympics game called Javelin Throw. Using two fingers, they each throw a straw “javelin” five times and measure the distance the straw flew to the nearest whole inch. The winner is the player whose average distance is the highest. Sam and Tanisha threw their javelins the following distances:

Question 1.
Draw a line plot to represent their data.
- Give the line plot a title and labels.
- Use a different color for Sam than for Tanisha, and fill in the legend to show which color is for which thrower.

Answer:
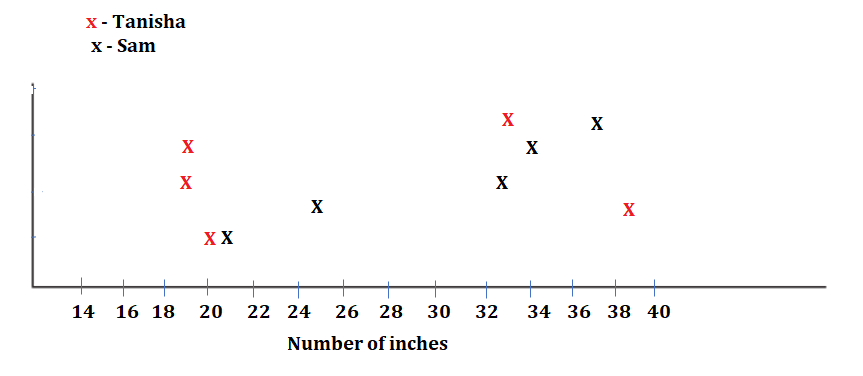
Explanation:
Data given:

Question 2.
CHALLENGE Sam calculated his average throw using the following expressions, but got stuck at the end. Complete his work to show his average throw.
21 + 25 + 33 + 34 + 37 = 150
150 ÷ 5 = ______________
Answer:
Average = 150 ÷ 3 = 30.
Explanation:
Given values = 21, 25, 33, 34, 37.
Total = 21 + 25 + 33 + 34 + 37 = 150.
Number of numbers given = 5.
Average = Total ÷ Number of numbers given
= 150 ÷ 5
=30.
Question 3.
CHALLENGE Write equations that Tanisha can use to calculate her average throw, then solve them.
Answer:
Average = Total ÷ Number of numbers given = 150 ÷ 5 =30.
Explanation:
Given values = 21, 25, 33, 34, 37.
Total = 21 + 25 + 33 + 34 + 37 = 150.
Number of numbers given = 5.
Average = Total ÷ Number of numbers given
= 150 ÷ 5
=30.