The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 7 Module 3 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 7 Module 3
Bridges in Mathematics Grade 3 Student Book Unit 7 Module 3 Session 1 Answer Key
Sixty Seconds in a Minute
Question 1.
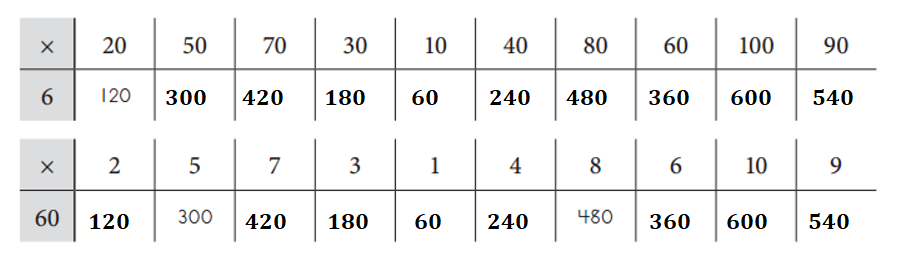
a. Fill in the tables below. Some of the answers have been filled in for you.
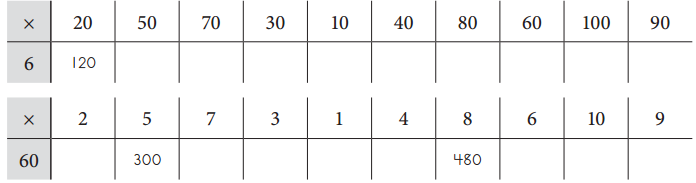
Answer:
Explanation:
Given Equations:
6 × 20 = 120.
6 × 50 = 300.
6 × 70 = 420.
6 × 30 = 180.
6 × 10 = 60.
6 × 40 = 240.
6 × 80 = 480.
6 × 60 = 360.
6 × 100 = 600.
6 × 90 = 540.
60 × 2 = 120.
60 × 5 = 300.
60 × 7 = 420.
60 × 3 = 180.
60 × 1 = 60.
60 × 4 = 240.
60 × 8 = 480.
60 × 6 = 360.
60 × 10 = 600.
60 × 9 = 540.
b. What do you notice about your answers?
Answer:
It is noticed that 6 multiplied by 10, gives the product having 0 in the end and viceversa.
Explanation:
It is noticed that ??
=> 6 multiplied by 10, gives the product having 0 in the end and viceversa.
Question 2.
There are 60 seconds in one minute.
a. How many seconds are there in 3 minutes? _________________
Answer:
180 seconds are there in 3 minutes.
Explanation:
3 minutes = ?? seconds.
Given:
1 Minute = 60 seconds.
3 minutes = ?? seconds.
=> 1 × ?? = 60 × 3
=> ?? = 180 seconds.
b. How many seconds are there in 5 minutes? _________________
Answer:
300 seconds are there in 5 minutes.
Explanation:
5 minutes = ?? seconds.
Given:
1 Minute = 60 seconds.
5 minutes = ?? seconds.
=> 1 × ?? = 60 × 5
=> ?? = 300 seconds.
c. How many seconds are there in 10 minutes? _________________
Answer:
600 seconds are there in 10 minutes.
Explanation:
10 minutes = ?? seconds.
Given:
1 Minute = 60 seconds.
10 minutes = ?? seconds.
=> 1 × ?? = 60 × 10
=> ?? = 600 seconds.
d. How many seconds are there in 4 minutes? _________________
Answer:
240 seconds are there in 4 minutes.
Explanation:
4 minutes = ?? seconds.
Given:
1 Minute = 60 seconds.
4 minutes = ?? seconds.
=> 1 × ?? = 60 × 4
=> ?? = 240 seconds.
e. How many seconds are there in 1\(\frac{1}{2}\) minutes? Show your work.
There are _____________ seconds in 1\(\frac{1}{2}\) minutes.
Answer:
90 seconds are there in 1\(\frac{1}{2}\) minutes.
There are 90 seconds in 1\(\frac{1}{2}\) minutes.
Explanation:
1\(\frac{1}{2}\) minutes = ?? seconds.
Given:
1 Minute = 60 seconds.
1\(\frac{1}{2}\) minutes = ?? seconds.
=> 1 × ?? = 60 × 1\(\frac{1}{2}\)
=> ?? = 60 × {[(1 × 2) + 1] ÷ 2}
=> ?? = 60 × [(2 + 1) ÷ 2]
=> ?? = 60 × \(\frac{3}{2}\)
=> ?? = 30 × \(\frac{3}{1}\)
=> ?? = 30 × 3 seconds.
=> ?? = 90 seconds.
Question 3.
CHALLENGE How many seconds are there in 1 hour? Show your work.
There are ______________ seconds in 1 hour.
Answer:
3600 seconds are there in 1 hour.
There are 3600 seconds in 1 hour.
Explanation:
1 hour = ?? seconds.
Given:
1 Minute = 60 seconds.
1 hour = 60 minutes.
1 hour = ?? seconds.
=> 1 hour = 60 × 60
=> 1 hour = 3600 seconds.
Bridges in Mathematics Grade 3 Student Book Unit 7 Module 3 Session 2 Answer Key
Building & Sketching Unit Fractions
Build as many different unit fractions as you can using your egg carton, tiles, and yarn. Sketch each of them on this sheet, and label each sketch with the fraction it shows.
Don’t forget to sketch the yarn as well as the “eggs” in these cartons. If you have extra cartons, see if you can find two or more different ways to build and sketch some of the fractions.
Answer:
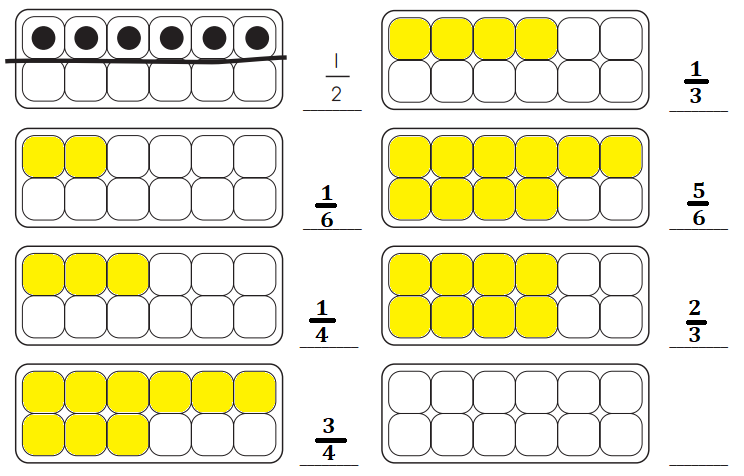
Explanation:
\(\frac{1}{3}\) = 12 × \(\frac{1}{3}\)
= 4 × \(\frac{1}{1}\)
= 4.
\(\frac{1}{6}\) = 12 × \(\frac{1}{6}\)
= 2 × \(\frac{1}{1}\)
= 2.
\(\frac{1}{4}\) = 12 × \(\frac{1}{4}\)
= 3 × \(\frac{1}{1}\)
= 3.
\(\frac{3}{4}\) = 12 × \(\frac{3}{4}\)
= 3 × \(\frac{3}{1}\)
= 9.
\(\frac{5}{6}\) = 12 × \(\frac{5}{6}\)
= 2 × \(\frac{5}{1}\)
= 10.
\(\frac{2}{3}\) = 12 × \(\frac{2}{3}\)
= 4 × \(\frac{2}{1}\)
= 8.
Modeling Egg Carton Fractions
Question 1.
Use your egg carton, yarn, and tiles to build sketch of each fraction you build.
ex: Build this fraction: \(\frac{1}{2}\)
Sketch your model:
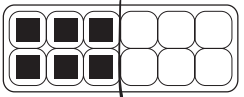
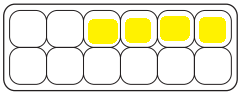
a. Build this fraction: \(\frac{1}{3}\)
Sketch your model:
Answer:
\(\frac{1}{3}\) = \(\frac{4}{12}\).
Explanation:
Given Fraction:
\(\frac{1}{3}\) = ??
Total tiles = 12.
=> 12 × \(\frac{1}{3}\)
= 4 × \(\frac{1}{1}\)
= 4.
b. Build this fraction: \(\frac{1}{4}\)
Sketch your model:

Answer:
\(\frac{1}{4}\) = \(\frac{3}{12}\).
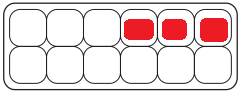
Explanation:
Given Fraction:
\(\frac{1}{4}\) = ??
Total tiles = 12.
=> 12 × \(\frac{1}{4}\)
= 3 × \(\frac{1}{1}\)
= 3.
c. Build this fraction: \(\frac{1}{6}\)
Sketch your model:

Answer:
\(\frac{1}{6}\) = \(\frac{2}{12}\).
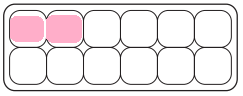
Explanation:
Given Fraction:
\(\frac{1}{6}\) = ??
Total tiles = 12.
=> 12 × \(\frac{1}{6}\)
= 2 × \(\frac{1}{1}\)
= 2.
Question 2.
Which is more, \(\frac{1}{4}\) of a dozen cookies or \(\frac{1}{3}\) of a dozen cookies?
a. How many more cookies is that?
Answer:
\(\frac{1}{3}\) of a dozen cookies is more than \(\frac{1}{4}\) of a dozen cookies by 1 more cookie.
Explanation:
Given Fractions:
\(\frac{1}{4}\) of a dozen cookies or \(\frac{1}{3}\) of a dozen cookies.
Conversion:
1 dozen = 12 cookies.
\(\frac{1}{4}\) = 12 × \(\frac{1}{4}\)
= 3 × \(\frac{1}{1}\)
= 3.
\(\frac{1}{3}\) = 12 × \(\frac{1}{3}\)
= 4 × \(\frac{1}{1}\)
= 4.
b. How do you know? Use labeled sketches, numbers, or words to explain your answer.
Answer:
By calculating how many cookies that is \(\frac{1}{3}\) and \(\frac{1}{4}\) of a dozen.
Explanation:
Given Fractions:
\(\frac{1}{4}\) of a dozen cookies or \(\frac{1}{3}\) of a dozen cookies.
Conversion:
1 dozen = 12 cookies.
\(\frac{1}{4}\) = 12 × \(\frac{1}{4}\)
= 3 × \(\frac{1}{1}\)
= 3.
\(\frac{1}{3}\) = 12 × \(\frac{1}{3}\)
= 4 × \(\frac{1}{1}\)
= 4.
Question 3.
Complete the equations.
8 + ___________ = 12
12 – ___________ = 9
3 × ___________ = 12
2 × ___________ = 12
___________ + 5 = 12
4 × ___________ = 16
12 ÷ 4 = ___________
12 – ___________= 2
16 ÷ 2 = ___________
12 ÷ ___________ = 6
12 + ___________ = 18
16 – ___________ = 12
Answer:
Equations:
8 + 4 = 12.
12 – 3 = 9.
3 × 4 = 12.
2 × 6 = 12.
7 + 5 = 12.
4 × 4 = 16.
12 ÷ 4 = 3.
12 – 10 = 2.
16 ÷ 2 = 8.
12 ÷ 2 = 6.
12 + 6 = 18.
16 – 4 = 12.
Explanation:
Missing numbers in the equations:
8 + ?? = 12.
=> ?? = 12 – 8
=> ?? = 4.
12 – ?? = 9.
=> 12 – 9 = ??
=> 3 = ??.
3 × ?? = 12.
=> ?? = 12 ÷ 3
=> ?? = 4.
2 × ?? = 12.
=> ?? = 12 ÷ 2
=> ?? = 6.
?? + 5 = 12.
=> ?? = 12 – 5
=> ?? = 7.
4 × ?? = 16.
=> ?? = 16 ÷ 4
=> ?? = 4.
12 ÷ 4 = ??.
=> 3 = ??
12 – ?? = 2.
=> 12 – 2 = ??
=> 10 = ??.
16 ÷ 2 = ??.
=> 8 = ??.
12 ÷ ?? = 6.
=> ?? = 6 × 12
=> ?? = 72.
12 + ?? = 18.
=> ?? = 18 – 12
=> ?? = 6.
16 – ?? = 12.
=> 16 – 12 = ??
=> 4 = ??.
Question 4.
CHALLENGE Write six different equations that each have 12 for an answer. You can use addition, subtraction, multiplication, or division, and numbers up to 1,000.
Answer:
Six different equations that each have 12 for an answer are:
1. 6 + 6 = 12.
2.36 ÷ 3 = 12.
3. 4 × 3 = 12.
4. 24 ÷ 2 = 12.
5. 2 × 6 = 12.
6. 72 ÷ 6 = 12.
Explanation:
Six different equations that each have 12 for an answer = ??.
1. 6 + 6 = 12.
2.36 ÷ 3 = 12.
3. 4 × 3 = 12.
4. 24 ÷ 2 = 12.
5. 2 × 6 = 12.
6. 72 ÷ 6 = 12.
Egg Carton Fractions
Bridges in Mathematics Grade 3 Student Book Unit 7 Module 3 Session 3 Answer Key
Fraction Fill & Compare
Question 1.
Fill in the shapes to show each fraction.
ex: \(\frac{1}{2}\)
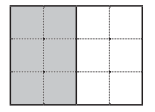
a. \(\frac{1}{3}\)
Answer:
\(\frac{1}{3}\) = \(\frac{4}{12}\).
Explanation:
\(\frac{1}{3}\) = ??
Given :
Total number of tiles = 12.
\(\frac{1}{3}\) = 12 × \(\frac{1}{3}\)
= 4 × \(\frac{1}{1}\)
= 4.
b. \(\frac{1}{4}\)

Answer:
\(\frac{1}{4}\) = \(\frac{3}{12}\).
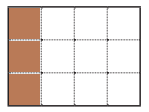
Explanation:
\(\frac{1}{4}\) = ??
Given :
Total number of tiles = 12.
\(\frac{1}{4}\) = 12 × \(\frac{1}{4}\)
= 3 × \(\frac{1}{1}\)
= 3.
c. \(\frac{1}{6}\)

Answer:
\(\frac{1}{6}\) = \(\frac{2}{12}\).
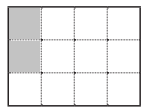
Explanation:
\(\frac{1}{6}\) = ??
Given :
Total number of tiles = 12.
\(\frac{1}{6}\) = 12 × \(\frac{1}{6}\)
= 2 × \(\frac{1}{1}\)
= 2.
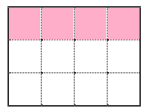
d. \(\frac{2}{3}\)

Answer:
\(\frac{2}{3}\) = \(\frac{8}{12}\).
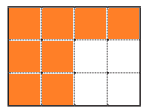
Explanation:
\(\frac{2}{3}\) = ??
Given :
Total number of tiles = 12.
\(\frac{2}{3}\) = 12 × \(\frac{2}{3}\)
= 4 × \(\frac{2}{1}\)
= 8.
e. \(\frac{5}{6}\)

Answer:
\(\frac{5}{6}\) = \(\frac{10}{12}\).
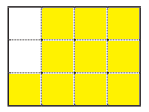
Explanation:
\(\frac{5}{6}\) = ??
Given :
Total number of tiles = 12.
\(\frac{5}{6}\) = 12 × \(\frac{5}{6}\)
= 2 × \(\frac{5}{1}\)
= 10.
Question 2.
Look at the fractions you shaded in above. Use them to help complete each number sentence by writing <, >, or =.
ex: \(\frac{1}{4}\) > \(\frac{1}{6}\)
a. \(\frac{1}{4}\) _______________ \(\frac{1}{3}\)
Answer:
\(\frac{1}{4}\) < \(\frac{1}{3}\).
Explanation:
Given Equations:
\(\frac{1}{4}\) = 0.25.
\(\frac{1}{3}\) = 0.33.
=> \(\frac{1}{4}\) is lesser than \(\frac{1}{3}\).
b. \(\frac{1}{3}\) _______________ \(\frac{2}{6}\)
Answer:
\(\frac{1}{3}\) = \(\frac{2}{6}\).
Explanation:
Given Equations:
\(\frac{1}{3}\) = 0.33.
\(\frac{2}{6}\) = \(\frac{1}{3}\) = 0.33
=> \(\frac{1}{3}\) is equal to \(\frac{2}{6}\).
c. \(\frac{1}{3}\) _______________ \(\frac{2}{3}\)
Answer:
\(\frac{1}{3}\) is lesser than \(\frac{2}{3}\).
Explanation:
Given Equations:
\(\frac{1}{3}\) = 0.33.
\(\frac{2}{3}\) = 0.67.
=> \(\frac{1}{3}\) is lesser than \(\frac{2}{3}\).
d. \(\frac{3}{3}\) _______________ 1
Answer:
\(\frac{3}{3}\) = 1.
Explanation:
Given Equations:
\(\frac{3}{3}\) = \(\frac{1}{1}\) = 1.
1.
=> latex]\frac{3}{3}[/latex] is equal to 1.
e. \(\frac{3}{6}\) _______________ \(\frac{3}{4}\)
Answer:
\(\frac{3}{6}\) < \(\frac{3}{4}\).
Explanation:
Given Equations:
\(\frac{3}{6}\) = \(\frac{1}{2}\) = 0.50.
\(\frac{3}{4}\) = 0.75
\(\frac{3}{6}\) is lesser than \(\frac{3}{4}\).
Question 3.
Fill in the shapes to show each fraction.
ex: \(\frac{1}{3}\)
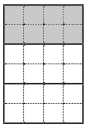
a. \(\frac{1}{4}\)

Answer:
\(\frac{1}{4}\) = \(\frac{6}{24}\).

Explanation:
\(\frac{1}{4}\) = ??
Given :
Total number of tiles = 24.
\(\frac{1}{4}\) = 24 × \(\frac{1}{4}\)
= 6 × \(\frac{1}{1}\)
= 6.
b. \(\frac{1}{6}\)

Answer:
\(\frac{1}{6}\) = \(\frac{4}{24}\).
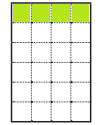
Explanation:
\(\frac{1}{6}\) = ??
Given :
Total number of tiles = 24.
\(\frac{1}{6}\) = 24 × \(\frac{1}{6}\)
= 4 × \(\frac{1}{1}\)
= 4.
c. \(\frac{1}{8}\)

Answer:
\(\frac{1}{8}\) = \(\frac{3}{24}\).
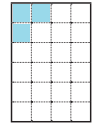
Explanation:
\(\frac{1}{8}\) = ??
Given :
Total number of tiles = 24.
\(\frac{1}{8}\) = 24 × \(\frac{1}{8}\)
= 3 × \(\frac{1}{1}\)
= 3.
d. \(\frac{3}{8}\)

Answer:
\(\frac{3}{8}\) = \(\frac{9}{24}\).

Explanation:
\(\frac{3}{8}\) = ??
Given :
Total number of tiles = 24.
\(\frac{3}{8}\) = 24 × \(\frac{3}{8}\)
= 3 × \(\frac{3}{1}\)
= 9.
e. \(\frac{7}{8}\)

Answer:
\(\frac{7}{8}\) = \(\frac{21}{24}\).

Explanation:
\(\frac{7}{8}\) = ??
Given :
Total number of tiles = 24.
\(\frac{7}{8}\) = 24 × \(\frac{7}{8}\)
= 3 × \(\frac{7}{1}\)
= 21.
Question 4.
Write each of these fractions where they belong on the number line: \(\frac{1}{4}\), \(\frac{1}{6}\), \(\frac{7}{8}\), \(\frac{2}{3}\).

Answer:
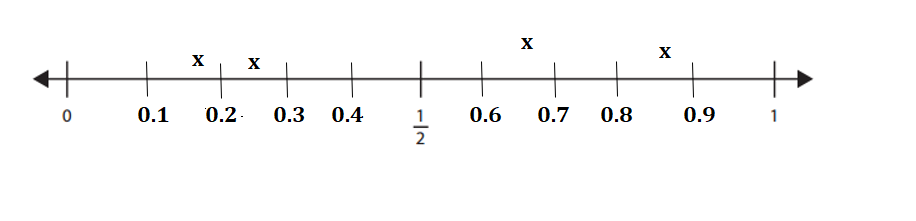
Explanation:
Given Fractions:
\(\frac{1}{4}\) = 0.25.
\(\frac{1}{6}\) = 0.167
\(\frac{7}{8}\) = 0.875
\(\frac{2}{3}\) = 0.67.
Bridges in Mathematics Grade 3 Student Book Unit 7 Module 3 Session 4 Answer Key
Fraction Fiction
Solve the story problems below. Use numbers, sketches, or words to show your work.
Question 1.
Sophia is writing and illustrating a picture book about chickens. The book will have 12 pages in all. She has finished 6 pages. What fraction of the book has Sophia finished?
Answer:
Fraction of the book has Sophia finished = \(\frac{1}{2}\).
Explanation:
Number of pages in the book in all = 12.
Number of pages she has finished = 6.
Fraction of the book has Sophia finished = Number of pages she has finished ÷ Number of pages in the book in all
= 6 ÷ 12
= 1 ÷ 2 or \(\frac{1}{2}\).
Question 2.
On one page, Sophia shows chickens’ nests in the henhouse. There are 12 nests. Chickens are sitting in 9 of the nests.
a. What fraction of the nests have chickens sitting in them?
Answer:
Fraction of the nests have chickens sitting in them = \(\frac{3}{4}\).
Explanation:
Number of nests there are = 12.
Number of chickens sitting in the nests = 9.
Fraction of the nests have chickens sitting in them = Number of chickens sitting in the nests ÷ Number of nests there are
= 9 ÷ 12
= 3 ÷ 4 or \(\frac{3}{4}\).
b. What fraction of the nests are empty?
Answer:
Fraction of the nests are empty = \(\frac{1}{3}\).
Explanation:
Number of nests there are = 12.
Number of chickens sitting in the nests = 9.
Number of nests are empty = Number of nests there are – Number of chickens sitting in the nests
= 12 – 9
= 3.
Fraction of the nests are empty = Number of nests are empty ÷ Number of nests there are
= 3 ÷ 9
= 1 ÷ 3 or \(\frac{1}{3}\).
Question 3.
On another page, Sophia shows 12 eggs in a bowl in the kitchen. Two-thirds of the 12 eggs will be used in a cake. How many eggs are for the cake?
Answer:
Number of eggs are for a cake = 8.
Explanation:
Number of eggs in a bowl in the kitchen Sophia shows = 12.
Number of eggs are used in a cake = Two-thirds of the 12 eggs.
Number of eggs are for a cake = Number of eggs are used in a cake × Number of eggs in a bowl in the kitchen Sophia shows
= \(\frac{2}{3}\) × 12
= \(\frac{2}{1}\) × 4
= 8.
Question 4.
On another page, Sophia has written a story problem for her friends to solve. It says, “Last week, 5 of my chickens laid 1 egg, 3 of my chickens laid 2 eggs, and 4 of my chickens laid 3 eggs. How many eggs in all?”
a. Write an equation to represent Sophia’s story problem. Use a letter to stand for the unknown number.
Answer:
Total number of eggs in all = 6.
Explanation:
Number of eggs 5 of my chickens laid = 1.
Number of eggs 3 of my chickens laid = 2.
Number of eggs 4 of my chickens laid = 3.
Total number of eggs in all = Number of eggs 5 of my chickens laid + Number of eggs 3 of my chickens laid + Number of eggs 4 of my chickens laid
= 1 + 2 + 3
= 3 + 3
= 6.
b. Solve the problem. Show all your work.
Answer:
Total number of eggs all chicken laid in all are 6.
Explanation:
Number of eggs 5 of my chickens laid = 1.
Number of eggs 3 of my chickens laid = 2.
Number of eggs 4 of my chickens laid = 3.
Total number of eggs in all = Number of eggs 5 of my chickens laid + Number of eggs 3 of my chickens laid + Number of eggs 4 of my chickens laid
= 1 + 2 + 3
= 3 + 3
= 6.
Bridges in Mathematics Grade 3 Student Book Unit 7 Module 3 Session 5 Answer Key
Introducing Dozens of Eggs
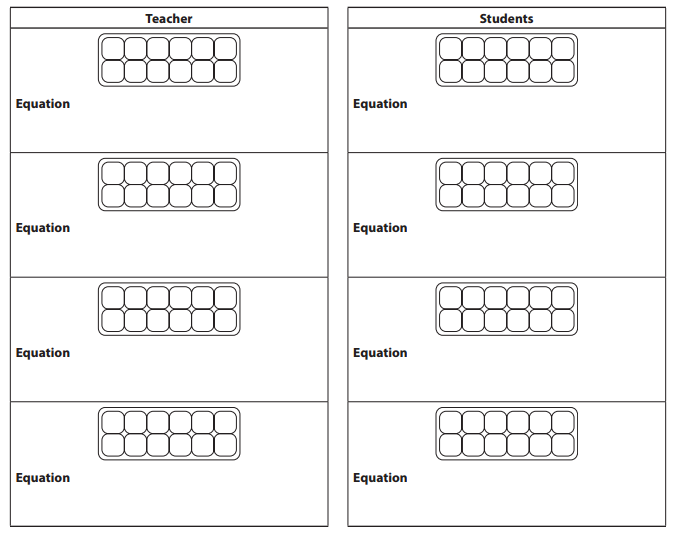
Work Place Instructions 7A Dozens of Eggs
Each pair of players needs:
- 2 Dozens of Eggs Record Sheets
- 1 deck of Dozens of Eggs Fraction Cards
- 1 egg carton
- 6 pieces of string or yarn
- 12 colored tiles
- colored pencils or crayons
1. Players shuffle the fraction cards and lay them face-down in a stack. Each player draws one card. The player with the larger fraction goes first. Players put the cards just drawn at the bottom of the stack. Players may build fractions on the Egg Carton Diagram if needed to determine which fraction is larger.
2. Player 1 draws a card from the top of the deck, reads the fraction out loud, and uses string and colored tiles to build a model of the fraction in the egg carton. Player 2 checks Player 1s work.
Jasmine Wow! I got a really big fraction on my first turn. So I’m going to divide the egg carton into 3 equal parts, and fill 2 of them, like this.
Sara I agree that \(\frac{2}{3}\) of the egg carton is 8 eggs, because there are 4 eggs in one-third of a carton.
3. Player 1 draws circles to represent that number of eggs in one of the diagrams on her record sheet and records that number of twelfths as a fraction on the sheet.
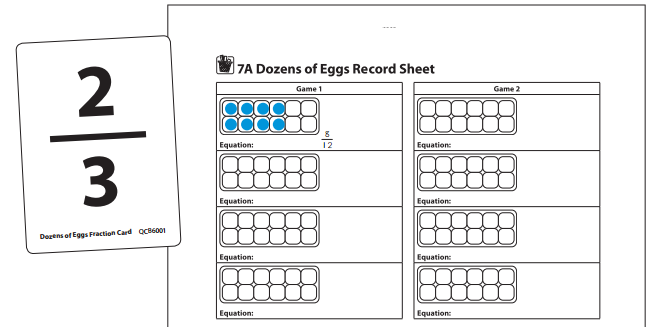
Jasmine I have to change \(\frac{2}{3}\) into twelfths, but that’s easy, because each egg is one-twelfth of the carton, so I got \(\frac{8}{12}\) on my first turn. I only need 4 more twelfths to fill this carton.Player 1 empties the egg carton diagram and puts the card in a discard stack. Then Player 2 takes a turn.
4. Players continue to take turns until one person has filled in all four cartons on the record sheet. Players should use a different color to record each new turn.
When all the cards in the deck have been used, shuffle the deck and use it again.
5. On each turn, players must put all of the eggs in one carton. However, players may begin to fill another carton before the first is completely filled.
6. If the fraction drawn does not fit into one of the cartons, the player misses that turn.
7. When a carton is filled, the player writes an equation by inserting plus signs between the fractions for that carton and showing them equal to 1 whole.
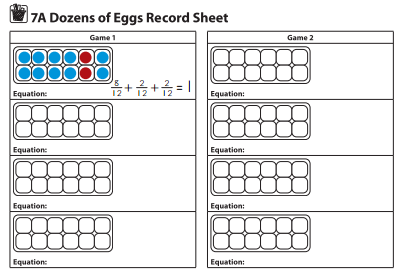
8. The winner is the first player to fill all four cartons on his record sheet. If Player 1 is the first to fill all four cartons, Player 2 may take one last turn.
Game Variations
A. Players work together to fill all four cartons on a single record sheet rather than playing against each other.
B. Players begin with all four cartons filled, by drawing 12 circles in each of the cartons and writing at the start of each equation line. Then each player subtracts the fractions that are written on the cards they get, crossing out that many eggs and subtracting that many twelfths. Players must subtract the entire fraction from one carton rather than splitting the fraction between two or more cartons. The winner is the first player to get rid of all the eggs from all four cartons.
Fraction Review
Question 1.
Lincoln has several chickens. Every day, he gathers eggs and puts them in a 12-egg carton. On Monday, he collected 3 eggs. On Tuesday, he collected 4 eggs. On Wednesday, he collected 2 more eggs.
a. What fraction of the egg carton did Lincoln fill on Monday? How do you know?
Answer:
Fraction of the egg carton Lincoln fills on Monday = \(\frac{1}{4}\)
Explanation:
Number of eggs carton he has = 12.
Number of eggs he collected on Monday = 3.
Number of eggs he collected on Tuesday = 4.
Number of eggs he collected on Wednesday = 2.
Total number of eggs he collects = Number of eggs he collected on Monday + Number of eggs he collected on Tuesday + Number of eggs he collected on Wednesday
= 3 + 4 + 2
= 7 + 2
= 9.
Fraction of the egg carton Lincoln fills on Monday = Number of eggs he collected on Monday ÷ 12
= 3 ÷ 12
= 1 ÷ 4 or \(\frac{1}{4}\)
b. What fraction of the egg carton did Lincoln fill on Tuesday? How do you know?
Answer:
Fraction of the egg carton Lincoln fills on Tuesday = \(\frac{1}{3}\).
Explanation:
Number of eggs carton he has = 12.
Number of eggs he collected on Monday = 3.
Number of eggs he collected on Tuesday = 4.
Number of eggs he collected on Wednesday = 2.
Total number of eggs he collects = Number of eggs he collected on Monday + Number of eggs he collected on Tuesday + Number of eggs he collected on Wednesday
= 3 + 4 + 2
= 7 + 2
= 9.
Fraction of the egg carton Lincoln fills on Tuesday = Number of eggs he colected on Tuesday ÷ 12
= 4 ÷ 12
= 1 ÷ 3 or \(\frac{1}{3}\)
c. If Lincoln put all of the eggs he gathered on Monday, Tuesday, and Wednesday into an egg carton, what fraction of the carton would be full? Show your work.
Answer:
Fraction of all eggs he puts in the carton = \(\frac{3}{4}\).
Explanation:
Number of eggs carton he has = 12.
Number of eggs he collected on Monday = 3.
Number of eggs he collected on Tuesday = 4.
Number of eggs he collected on Wednesday = 2.
Total number of eggs he collects = Number of eggs he collected on Monday + Number of eggs he collected on Tuesday + Number of eggs he collected on Wednesday
= 3 + 4 + 2
= 7 + 2
= 9.
Fraction of all eggs he puts in the carton = Total number of eggs he collects ÷ 12
= 9 ÷ 12
= 3 ÷ 4 or \(\frac{3}{4}\).
d. How many eggs does Lincoln need to take out so the egg carton will be only half full? How do you know?
Answer:
Number of eggs to be removed to kept in carton half full = 3.
Explanation:
Number of eggs carton he has = 12.
Number of eggs he collected on Monday = 3.
Number of eggs he collected on Tuesday = 4.
Number of eggs he collected on Wednesday = 2.
Total number of eggs he collects = Number of eggs he collected on Monday + Number of eggs he collected on Tuesday + Number of eggs he collected on Wednesday
= 3 + 4 + 2
= 7 + 2
= 9.
Half of a carton eggs = 12 ÷ 2
= 6.
=> Number of eggs to be removed to kept in carton half full = Total number of eggs he collects – 6
= 9 – 6
= 3.
Question 2.
Write each of these fractions where they belong on the number line: \(\frac{1}{3}\), \(\frac{1}{1}\), \(\frac{1}{6}\), \(\frac{5}{8}\), \(\frac{6}{12}\), \(\frac{1}{2}\)

Answer:
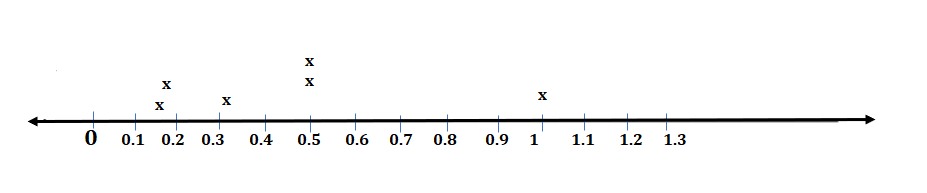
Explanation:
Given Fractions to represent on number line:
\(\frac{1}{3}\) = 0.33.
\(\frac{1}{1}\) = 1.
\(\frac{1}{6}\) = 0.167.
\(\frac{5}{8}\) = 0.625.
\(\frac{6}{12}\) = 0.50.
\(\frac{1}{2}\) = 0.50.