The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 6 Module 3 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 6 Module 3
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 3 Session 1 Answer Key
Round the Table
Question 1.
Round these numbers.
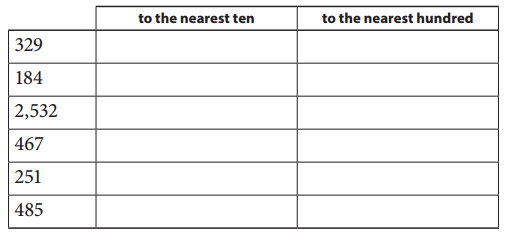
Answer:
Explanation:
1.329
To round off a number to tens we need to check the ones place as the ones place is more than 5 in the above question we can add 1 to the tens place but change the ones to zero, 329 is rounded off to 330.
To round off a number to hundreds we need to check the tens place as the tens place is less than 5 in the above question we need not change the hundreds place but change the tens and ones to zero, 329 is rounded off to 300.
2.184
To round off a number to hundreds we need to check the ones place as the tens place is less than 5 in the above question we need not change the hundreds place but change the tens and ones to zero, 184 is rounded off to 180.
To round off a number to hundreds we need to check the tens place as the tens place is more than 5 in the above question we can add 1 to the hundreds place by changing the tens and ones to zero, 184 is rounded off to 200.
3.2532
To round off a number to hundreds we need to check the ones place as the tens place is less than 5 in the above question we need not change the hundreds place but change the tens and ones to zero, 2532 is rounded off to 2530.
To round off a number to hundreds we need to check the tens place as the tens place is less than 5 in the above question we need not change the hundreds place but change the tens and ones to zero, 2532 is rounded off to 2500.
4.467
To round off a number to tens we need to check the ones place as the ones place is more than 5 in the above question we can add 1 to the tens place but change the ones to zero, 467 is rounded off to 470.
To round off a number to hundreds we need to check the tens place as the tens place is more than 5 in the above question we can add 1 to the hundreds place by changing the tens and ones to zero, 467 is rounded off to 500.
5.251
To round off a number to hundreds we need to check the ones place as the tens place is less than 5 in the above question we need not change the hundreds place but change the tens and ones to zero, 251 is rounded off to 250.
To round off a number to hundreds we need to check the tens place as the tens place is more than 5 in the above question we can add 1 to the hundreds place by changing the tens and ones to zero, 251 is rounded off to 300.
6.485
To round off a number to tens we need to check the ones place as the ones place is more than 5 in the above question we can add 1 to the tens place but change the ones to zero, 485 is rounded off to 490.
To round off a number to hundreds we need to check the tens place as the tens place is more than 5 in the above question we can add 1 to the hundreds place by changing the tens and ones to zero, 485 is rounded off to 500.
Question 2.
Emery Raccoon and his lunch guests used 329 spoons, 329 forks, and 329 knives. How many pieces of silverware did they use in all? Show your work.
Answer:
Total of 987 silverware was used for the lunch,
Explanation:
Number of spoons used = 329, Number of forks used = 329, Number of knives used = 329, Total number of silverware used = Number of spoons used + Number of forks used + Number of knives used = 329 + 329 + 329 = 987.
Question 3.
Multiply.
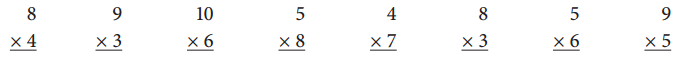
Answer:
Explanation:
By mental computation,
As the number to be added is 8 and the integral number value is 4, so to find the value we need to add 8 for 4 times, 8 × 4 = 8 + 8 + 8 + 8 = 32, hence 8 × 4 = 32.
By mental computation,
As the number to be added is 9 and the integral number value is 3, so to find the value we need to add 9 for 3 times, 9 × 3 = 9 + 9 + 9 = 27, hence 9 × 3 = 27.
Step 1: Multiply the integral value 6 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 6 × 0 = 0.
Step 2: Multiply the integral value 6 with the number in tens place, any number multiplied by 1 gives the same number itself, hence 6 × 1 = 6.
Therefore, 10 × 6 = 60.
By mental computation,
As the number to be added is 5 and the integral number value is 8, so to find the value we need to add 5 for 8 times, 5 × 8 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 40, hence 5 × 8 = 40.
By mental computation,
As the number to be added is 4 and the integral number value is 7, so to find the value we need to add 4 for 7 times, 4 × 7 = 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28, hence 4 × 7 = 28.
By mental computation,
As the number to be added is 8 and the integral number value is 3, so to find the value we need to add 8 for 3 times, 8 × 3 = 8 + 8 + 8 = 24, hence 8 × 3 = 24.
By mental computation,
As the number to be added is 5 and the integral number value is 6, so to find the value we need to add 5 for 6 times, 5 × 6 = 5 + 5 + 5 + 5 + 5 + 5 = 30, hence 5 × 6 = 30.
By mental computation,
As the number to be added is 9 and the integral number value is 5, so to find the value we need to add 9 for 5 times, 9 × 5 = 9 + 9 + 9 + 9 +9 = 45, hence 9 × 5 = 45.
Question 4.
Add or subtract.
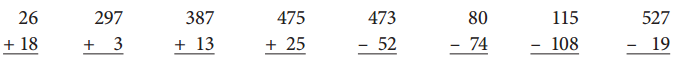
Answer:
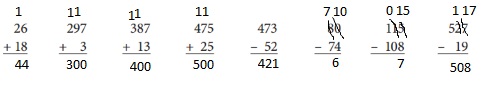
Explanation:
There are two 2-digit numbers given, first add numbers in the ones place and then lastly add numbers in the tens place, 26+18 = 44.
There are two 3-digit numbers given, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 297+3 = 300.
There are two 3-digit numbers given, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 387+13 = 400.
Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Rename 8 tens and 0 ones as “7 tens and 10 ones.” Subtract the ones.
Subtract the tens.
Rename 1 tens and 5 ones as “0 tens and 15 ones.” Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Rename 2 tens and 7 ones as “1 tens and 17 ones.” Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Question 5.
CHALLENGE Emery tore up 10 sheets to make 330 napkins. How many napkins did he make out of each sheet? Show your work.
Answer:
Number of napkins Emery made out of each sheet is 33.
Explanation:
Number of sheets = 10
Number of napkins made out of 10 sheets = 330
Number of napkins made out of each sheet = \(\frac{330}{10}\) = 33
Work Place Instructions 6C Guess My Quadrilateral
Each pair of players needs:
- 6C Guess My Quadrilateral Record Sheets (1 per player)
1 set of Quadrilateral Cards (use a set that belongs to one of the players)
riddle booklets made by classmates
1. Players work together to lay out all the cards from one of their sets of Quadrilateral Cards. Then they choose a riddle book written by a classmate.
2. Players open the book for clue 1, read and discuss the clue, and set aside any of the Quadrilateral Cards that do not fit the clue.
Sample Clue: My quadrilateral has 2 pairs of parallel sides.
Cathy So we can get rid of anything that’s not a square or a rectangle, right?
Tyson We have to keep the parallelograms and the rhombus, too. They have 2 pairs of parallel sides.
Cathy OK, so we’ll get rid of the trapezoids and all the weird quadrilaterals.
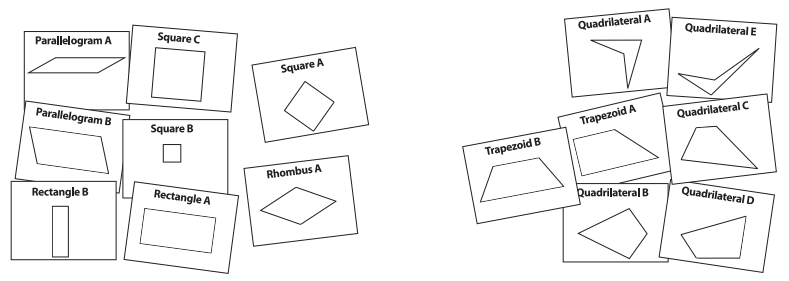
3. Players continue reading one clue at a time, discussing and putting aside the quadrilaterals that do not match each clue, until only one is left.
4. If players have more than one shape left, they look back over the clues to see if they forgot to put aside any of the shapes.
5. Players compare their answer to the one on the back of the riddle booklet.
6. Both players fill in the row on their record sheet for that riddle.
7. Players push all their Quadrilateral Cards back together, trade their riddle booklet in for another one, and solve the next riddle in the same way.
8. After players have solved at least five riddles, they answer the questions at the bottom of the record sheet.
Game Variations
A. Players may work alone to compete against a partner. Then players can compare answers after five riddles before checking answers on the riddle booklets. Players can assign one point for each correct riddle to determine a winner.
B. Players create additional riddles for some of the Quadrilateral Cards in their set.
C. Players determine the minimal number of clues necessary to identify a particular shape. In other words, which clues for each riddle were the most necessary? Could any have been eliminated?
Answer:
1. Rectangle
2. Parallelogram
3. Rhombus
4. Trapezoid
5. Square.
Explanation:
1.
Rectangle:
Opposite sides are equal.
All angles are equal.
Each angle measure 90 degrees.
Diagonals are equal.
Two pair of opposite sides are parallel.
2.
Parallelogram:
Two pairs opposite sides are parallel.
The opposite angles are equal.
Adjacent angles are supplementary.
Opposite sides are equal.
Diagonals bisect each other.
3.
Rhombus:
All sides are equal.
Diagonals bisect each other at right angles.
Sum of two adjacent angles is 180 degrees.
Opposite angles are equal.
Two pair of opposite sides are parallel.
4.
Trapezoid:
One pair of opposite sides are parallel.
Non parallel sides are not equal.
5.
Square:
All sides are equal.
All angles are equal.
Each angle is 90 degrees.
Two pair of opposite sides.
Diagonals are equal.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 3 Session 2 Answer Key
Game Night
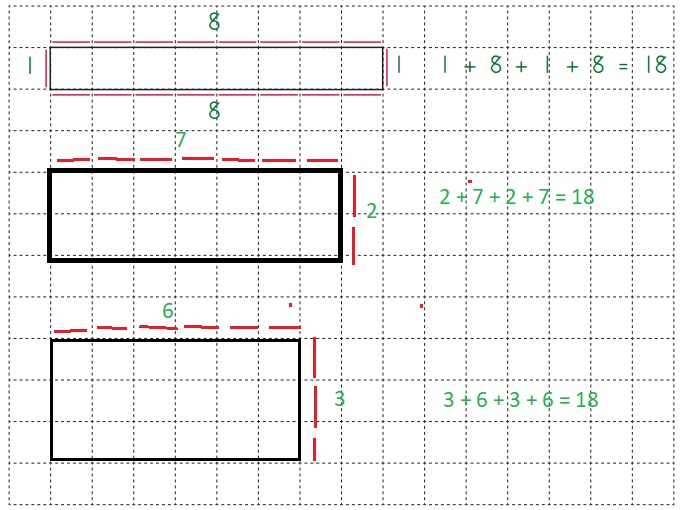
Rodney Rabbit invited 17 of his pals over to play board games. Use tiles and red linear units to build as many different rectangular arrays as you can that allow all 18 game players to sit at the same table.
Question 1.
Sketch each array on the grid below. Use a red colored pencil to mark the perimeter. Label the width and the length, and write an equation to show that the perimeter is 18 linear units. The first one is done for you as an example.
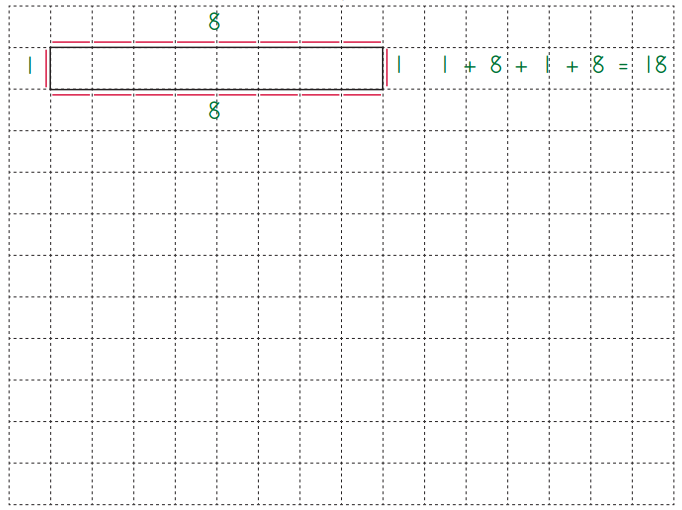
Answer:
Question 2.
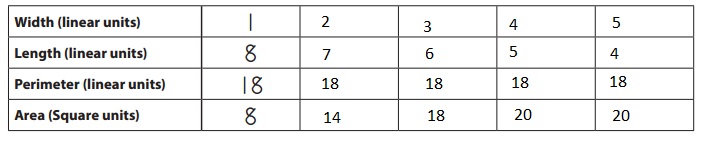
Record the dimensions, perimeter, and area of each of the rectangular arrays you built on the chart below.
Note: The area of each array is the number of tiles it took to build it.
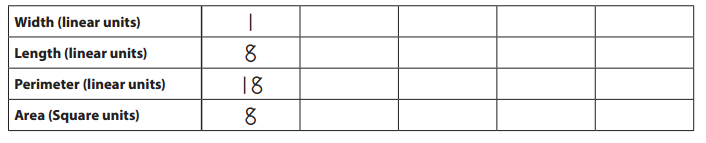
Answer:
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 3 Session 3 Answer Key
Metric Rectangles Record Sheet
Question 1.
Look at the six rectangles on the Metric Rectangles sheet. Write the letters of all the rectangles where you think they belong in the boxes below, in order from the smallest area to the largest area.

Answer:


Question 2.
Use your base ten pieces to find the area of each rectangle in square centimeters, and write an equation to show your work. Think of math shortcuts to help you determine the number of square centimeters, so you don’t have to count each unit separately.
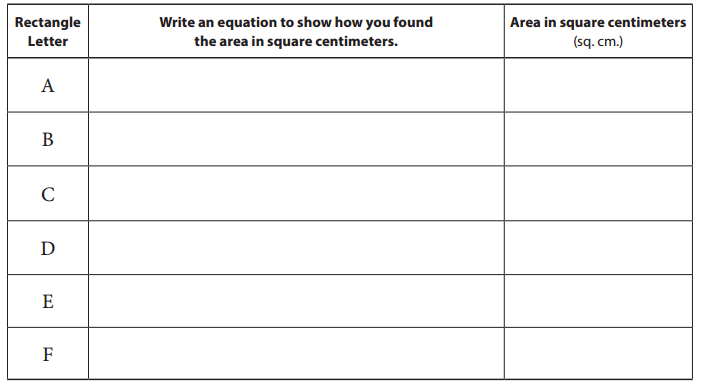
Answer:
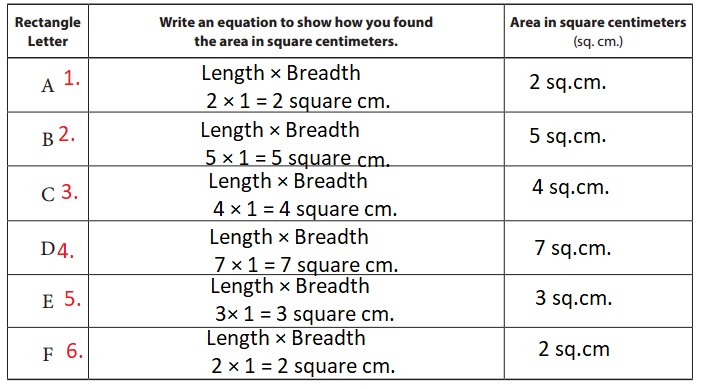
Question 3.
What do you think is the most efficient way to find the area of a rectangle? Use numbers, sketches, or words to describe your shortcut.
Answer:
The most effective way to find the area of a rectangle is by using multiplication,
Explanation:
As we know that multiplication means repeated addition, therefore using multiplication instead of addition is more effective way to find the area.
Area & Perimeter
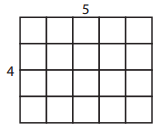
Question 1.
Find the area and perimeter of each rectangle. Area is the total amount of space covered by the rectangle. Perimeter is the distance around the rectangle.
ex:
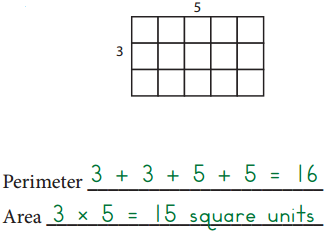
a.
Perimeter __________________
Area __________________
Answer:
Perimeter=18 units
Area=20 square units
Explanation:
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 5 + 5 + 4 + 4 =18 units.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 5 × 4 = 20 square units.
b.
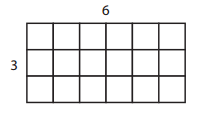
Perimeter __________________
Area __________________
Answer:
Perimeter=18 units
Area=18 square units
Explanation:
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 6 + 6 + 3 + 3 =18 units.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 6 × 3 = 18 square units.
c.
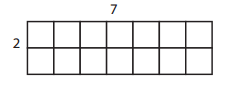
Perimeter __________________
Area __________________
Answer:
Perimeter=18 units
Area=14 square units
Explanation:
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 7 + 7 + 2 + 2 =18 units.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 7 × 2 = 14 square units.
Question 2.
Find the area and perimeter of this shape. Show all your work.
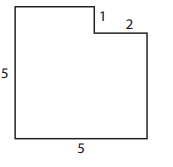
Perimeter __________________
Area __________________
Answer:
Perimeter=16 units
Area=23 units
Explanation:
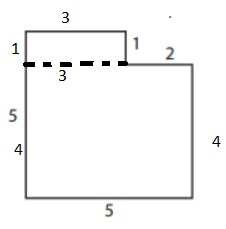
Perimeter is the distance around the figure.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 5 + 5 + 4 + 2 + 1 + 3 =20 units.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 3 × 1 = 3 square units
Area ( A2) = Length × Breadth
= 5 × 4 = 20 square units.
Total Area = A1 + A2
=3 + 20 = 23 square units
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 3 Session 4 Answer Key
Bayard Owl’s Borrowed Tables
Emery Raccoon’s new friend, Bayard Owl, is planning a birthday party for himself. He has borrowed 24 small square tables from Emery, and wants to push them together to make one large rectangular table where all his friends can sit together.
Question 1.
Use your tiles to build as many different rectangular tables as you can. You have to use all 24 tiles for each table, and you can’t leave any holes or gaps.
a. Sketch each of the tables you make on the grid below. Label its side lengths, and write two equations: one to show what the perimeter is and how you found it, and another to show what the area is and how you found it.

Answer:
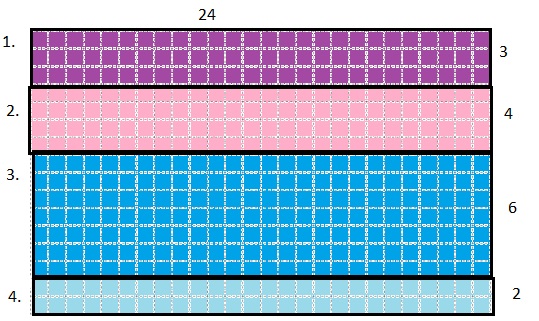
1.
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 24 + 24 + 3 + 3 =54 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 24 × 3 = 72 square cm.
2.
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 24 + 24 + 4 + 4 =56 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 24 × 4 = 96 square cm.
3.
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 24 + 24 + 6 + 6 =60 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 24 × 6 = 144 square cm.
4.
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 24 + 24 + 2 + 2 = 52 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 24 × 2 = 48 square cm.
b. Which table do you think Bayard Owl should use for his party? Why?
Answer:
Bayard Owl can use the third table since it has highest perimeter and area.
Measuring to Find the Area & Perimeter
Use the centimeter side of a ruler to measure each rectangle below. Label the dimensions of the rectangle, and use the information to find the area and perimeter. Show your work.
Area is the total amount of space covered by the rectangle, and perimeter is the total distance around the rectangle.
ex:
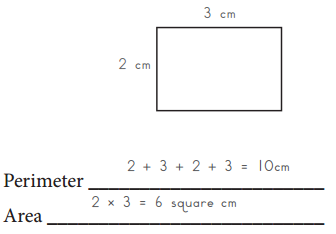
Question 1.

Perimeter __________________
Area __________________
Answer:
Perimeter=16 cm.
Area=15 square cm.
Explanation:
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 5 + 5 + 3 + 3 =16 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 5 × 3 = 15 square cm.
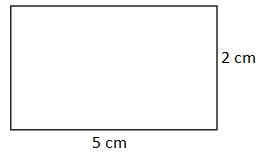
Question 2.

Perimeter __________________
Area __________________
Answer:
Perimeter=16 cm.
Area=12 square cm.
Explanation:
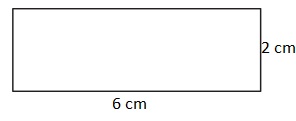
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 7 + 7 + 2 + 2 =18 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 7 × 2 = 14 square cm.
Question 3.

Perimeter __________________
Area __________________
Answer:
Perimeter=18 cm.
Area=20 square cm.
Explanation:
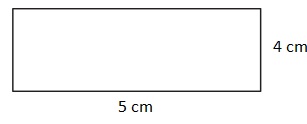
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 4 + 4 + 5 + 5 =18 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area = Length × Breadth
= 4 × 5 = 20 square cm.
Question 4.
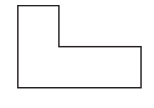
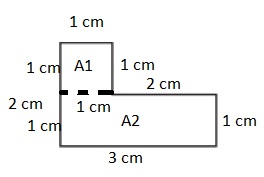
CHALLENGE. Measure and label the figure below, then find its perimeter and area.
Perimeter __________________
Area __________________
Answer:
Perimeter= 10 cm.
Area= 4 square cm.
Explanation:
Perimeter is the distance around the rectangle.
So the perimeter of the above figure is
Perimeter = Sum of all the sides
= 1 + 1 + 2 + 1 + 3 + 2 =10 cm.
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 1 × 1 = 1 square units
Area ( A2) = Length × Breadth
= 3 × 1 = 3 square cm.
Total Area = A1 + A2
=1 + 3 = 4 square cm.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 3 Session 5 Answer Key
The Goat Twins’ Table
One day when Emery was in town doing errands, the Goat Twins, Zachary and Whackery, decided to surprise him. They got some of Emery’s small square tables out of the shed and arranged them in an unusual way. When Emery got home, he laughed at the twins and said, “OK, if the two of you are so smart, can you tell me the area of this big new table you’ve arranged?”
Question 1.
Help the twins. How can they find the area of the table they made without having to count all the small squares?

Answer:
Total area covered by the figure is equal 30 square units.
Explanation:
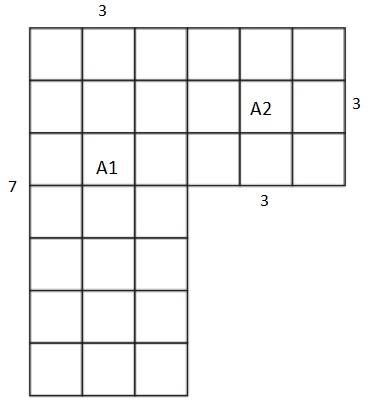
Area is the total amount of space covered by the figure.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 7 × 3 = 21 square units
Area ( A2) = Length × Breadth
= 3 × 3 = 9 square units.
Total Area = A1 + A2
=21 + 9 = 30 square units.
Question 2.
Can you think of more than one way to solve this problem?
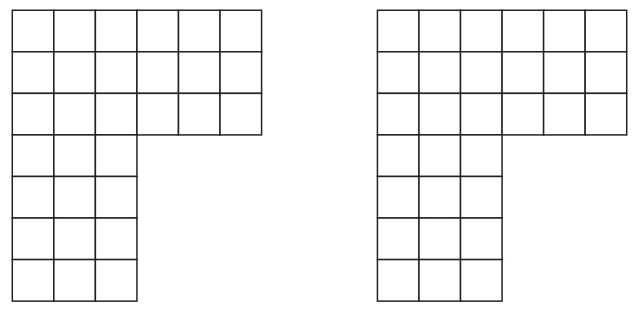
Answer:
Count the number of squares it gives us the area of the figure.
Number of squares = 30
So area is 30 square units.
Work Place Instructions 6D Area or Perimeter
Each pair of players needs:
- 6D Area or Perimeter Record Sheets, 1 for each player
- 1 or more sheets of 6D Area or Perimeter Grid Paper
- 80 colored tiles or 2 sets of red linear units
Players use tiles if rolling for area; they use red linear units if rolling for perimeter two 1-6 dice - 1 colored pencil
1. Players decide together if they are going to roll for and keep the area or the perimeter the same for the rectangles they build. They each circle that word on their own record sheet.
2. One player rolls the dice. Using their individual record sheets, each player uses column 1 to record the numbers rolled and column 2 to record the product of the two numbers.
3. If players are working with area, they count out tiles to equal the product of the two numbers rolled. If they’re working with perimeter, they count out red linear units to equal the product of the two numbers rolled.
4. Players lay their tiles or linear units out on the grid paper to form a rectangle.
- Players may need to use more than 1 sheet of grid paper to build some rectangles.
- The grid paper is optional for players working with area and using tiles. If players are working with perimeter and using the red linear pieces, they need to lay out the pieces on the grid paper.
5. Players record the dimensions, area, and perimeter of the rectangle they made on their record sheets. Some products will not work as perimeters for rectangles. In that case, players just write “impossible” on the line for that roll.
6. Players work together to rearrange the tiles or red linear units to form another rectangle (with the same area or perimeter as rolled for the first rectangle) and record the information for it on the next line of the record sheet.
- Players keep rearranging and forming rectangles with that same area or perimeter until they can’t make any more.
- Players use a colored pencil to draw a line across the table below the information for the last rectangle they were able to make for a pair of numbers.
7. Players roll the dice and build as many rectangles as they can for the new area or perimeter.
- Players must continue to work with the type of measurement they chose for that record sheet, rather than switching from area to perimeter or vice versa.
- If players roll two numbers they’ve already rolled today, or two numbers that make the same product, they roll again.
8. Players keep rolling and building rectangles until they fill the table or run out of time.
Game Variations
A. Use one 1-6 die and one 4-9 die instead of two 1-6 dice.
B. Use two 4-9 dice instead of two 1-6 dice.
Answer:
A: The rectangles in the first case will be more in number,
B: The rectangles in the second case will be less in number compared to case A,
Explanation:
A: As one side of the rectangle ranges between 1 to 6 and the other side of the rectangle ranges between 4 to 9 we obtain more rectangles on the table,
B: As both the sides of the rectangle ranges 4 to 9 we obtain less rectangles on the table compared to case A, there is more probability of obtaining rectangles of equal dimensions which means that we may obtain squares.
More of the Twins’ Tables
Question 1.
As soon as Emery had to go into town again, the Goat Twins, Zachary and Whackery, got up to their old tricks. Here are 4 different arrangements they made with Emery’s small square tables. Find the area of each. Use lines or loops, along with numbers and equations to show how you got your answers.
a.
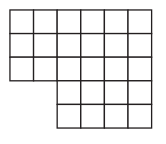
Area = ______________ sq. units
Answer:
Total area covered by the figure is equal 26 square units.
Explanation:
Area is the total amount of space covered by the figure.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 3 × 2 = 6 square units
Area ( A2) = Length × Breadth
= 4 × 5 = 20 square units.
Total Area = A1 + A2
=6 + 20 = 26 square units.
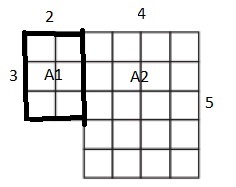
b.

Area = ______________ sq. units
Answer:
Area is the total amount of space covered by the figure.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 7 × 3 = 21 square units
Area ( A2 ) = Length × Breadth
= 3 × 3 = 9 square units.
Area ( A3 ) = Length × Breadth
3 × 2 = 6 square units.
Total Area = A1 + A2 + A3
=21 + 9 + 6= 36 square units.
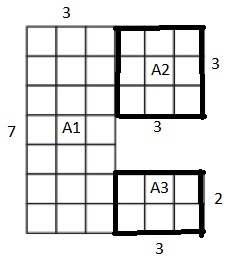
c.
Area = ______________ sq. units
Answer:
The total area covered by the figure is equal to 41 square units.
Explanation:
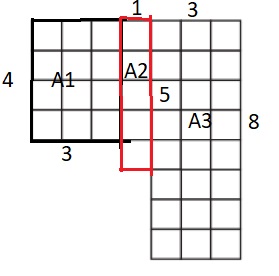
Explanation:
Area is the total amount of space covered by the figure.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 4 × 3 = 12 square units
Area ( A2 ) = Length × Breadth
= 5 × 1 = 5 square units.
Area ( A3 ) = Length × Breadth
8 × 3 = 24 square units.
Total Area = A1 + A2 + A3
=12 + 5 + 24= 41 square units.
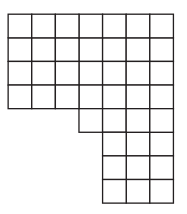
d.
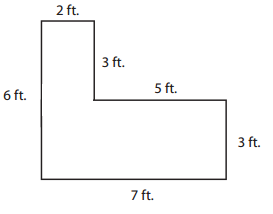
Area = ______________ sq. units
Answer:
Area of the above figure is equal to 27 square units.
Explanation:
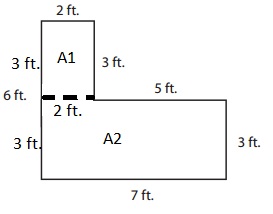
Area is the total amount of space covered by the rectangle.
So the area of the above figure is
Area ( A1 ) = Length × Breadth
= 3 × 2 = 6 square units.
Area ( A2) = Length × Breadth
= 7 × 3 = 21 square units.
Total Area = A1 + A2
=6 + 21 = 27 square units.
Question 2.
Here is a little sketch map of Emery’s rectangular backyard. The perimeter of the yard is 30 yards. Use that information, along with the picture, to figure out the length of the side labeled s.

Side s is ____________ yards long.
Answer:
Sides s is 5 yards long.
Explanation:
Perimeter is the distance around the rectangle.
So perimeter of the above figure is equal to the sum of all the sides.
10 + 10 + 5 + s = 30
25 + s = 30
s = 30 – 25
s = 5.