The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 6 Module 1 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 6 Module 1
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 1 Session 1 Answer Key
Mixed Review: Fractions, Multiplication & Division
Solve each problem below. Show your work using numbers, sketches, or words. Remember to label your answers with the correct units when you need to.
Question 1.
Robin and Cody are collecting stamps. Their stamp books are exactly the same size, with the same number of pages. Robin’s stamp book is \(\frac{2}{3}\) full. Cody’s stamp book is \(\frac{3}{4}\) full. Whose stamp book is more full? How do you know?
Answer:
Cody’s stamp book is more full than robin’s stamp book,
Explanation:
Robin’s stamp book is \(\frac{2}{3}\) full.
Cody’s stamp book is \(\frac{3}{4}\) full.
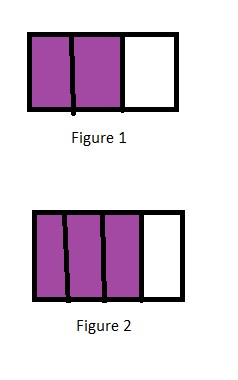
Let us assume that figure 1 represents the stamp book of Robin and figure 2 represents the stamp book of Cody.
Since figure 2 is more shaded than figure 1 so we can say that Cody’s stamp book is more full than Robin.
Question 2.
Robin has a page of her stamp book that is \(\frac{1}{3}\) full. Cody has a page of his stamp book that is \(\frac{2}{6}\) full. Whose page is more full? How do you know?
Answer:
Both Robin and Cody have same number of stamp pages,
Explanation:
Robin has a page of her stamp book that is \(\frac{1}{3}\) full.
Cody has a page of his stamp book that is \(\frac{2}{6}\) full {which is equal to \(\frac{1}{3}\)}.
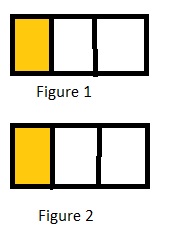
Let us assume that figure 1 represents the stamp book of Robin and figure 2 represents the stamp book of Cody.
Since figure 1 is equally shaded as figure 2.
So Robin and Cody as equal number of stamp pages
Question 3.
One of Robin’s pages has 6 out of 12 spaces full.
a. Write a fraction that represents how full the page is. ________________
Answer:
\(\frac{6}{12}\)
Explanation:
Number of spaces=12
Number of spaces filled by Robin=6
Fraction=\(\frac{6}{12}\)
=\(\frac{1}{2}\)
b. Write another fraction that tells how full the page is. ________________
Answer:
\(\frac{2}{4}\)
Explanation:
The another fraction is \(\frac{1}{2}\) × \(\frac{2}{2}\) = \(\frac{2}{4}\)
Question 4.
On one page of Robin’s stamp book, she has arranged her stamps in a 7-by-6 array. How many stamps are on this page?
Answer:
There are total of 42 stamps on this page,
Explanation:
7 by 6 array refers to 7 rows and 6 columns
Total number of stamps on this page = 7 × 6 = 42 stamps.
Question 5.
On one page of Cody’s stamp book, he has 54 stamps. The stamps are organized in 6 groups. How many stamps are in each group?
Answer:
There are 9 stamps in each group,
Explanation:
Total number of stamps on one page of Cody’s stamp book = 54, Number of groups = 6, Number of stamps in each group = \(\frac{Total number of stamps on one page of Cody’s stamp book}{Number of groups }\) = \(\frac{54}{6}\) = 9 stamps.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 1 Session 2 Answer Key
What Makes a Rectangle So Special?
All quadrilaterals have 4 sides and 4 corners. So, what makes a rectangle special?
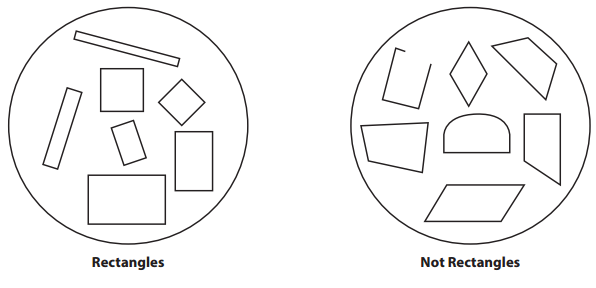
Question 1.
List at least 4 attributes that are shared by all of the shapes in the Rectangles group.
Answer:
In a rectangle:
Opposite sides are equal.
All the angles in a rectangle are equal.
Each angle is equal to 90 degrees.
Diagonals are equal in a rectangle.
Question 2.
List at least 4 reasons the shapes in the Not Rectangles group can’t be in the Rectangles group.
Answer:
The shapes in the Not Rectangles group can’t be in the Rectangles group because:
They have only one pair of parallel lines.
All angles are not equal.
All angles are not equal to 90 degrees.
Diagonals are not equal.
Shape Sorting
Question 1.
Walt sorted some shapes into these two groups.
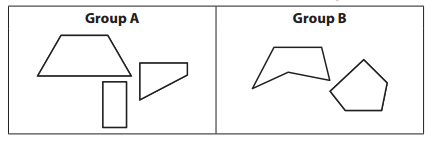
a. Circle the shape that belong in group B.
Answer:
b. What do the shapes in group B have in common?
Answer:
The similarity between the shapes in group B and the above encircled shapes is that they are five sided figure that is pentagon.
Question 2.
How can you tell if a shape is a hexagon?
a. Circle all the hexagons.
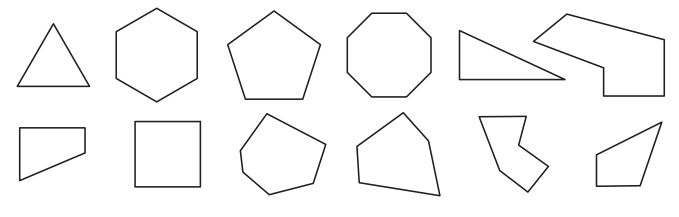
Answer:
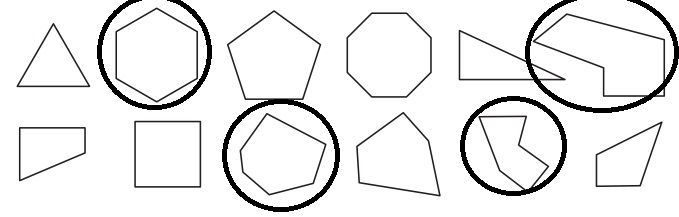
Explanation:
Hexagon means a plane figure with six straight sides, six vertices and six angles.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 1 Session 3 Answer Key
Shape Poster Project
You and your partner are going to make a poster about _______________.
After someone reads your poster, they should know all about the attributes of your shape, and be able to tell what makes it a special quadrilateral.
Your poster must include:
A title that tells the name of your quadrilateral
The slip of paper from your teacher with examples and nonexamples of your quadrilateral
Words or labeled sketches to describe at least 4 attributes of your quadrilateral
Words or labeled sketches that give at least 4 reasons the shapes that are in the other group are not examples of your quadrilateral
Drawings that show 2 more examples of your quadrilateral and 2 more nonexamples of your quadrilateral
A sentence at the bottom that tells what sets your quadrilateral apart from all the other kinds of quadrilaterals and makes it special
Make your poster:
- Neat
- Colorful
- Informative
- Easy to read and understand
- Fun!
Answer:
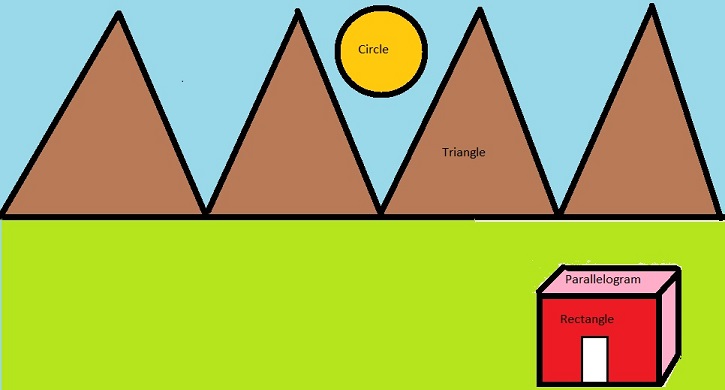
Explanation:
The poster is made by using the shapes like circle, triangle, rectangle and parallelogram, the poster satisfies the symmetry.
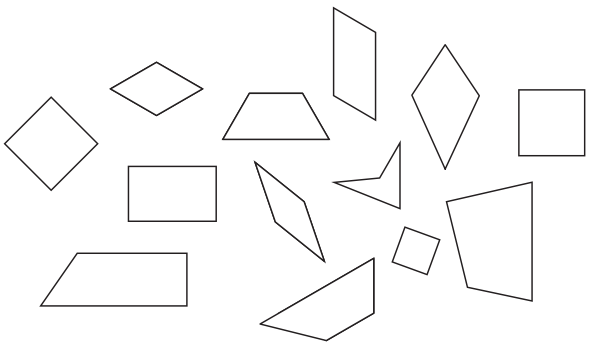
Attributes of Quadrilaterals
Question 1.
Identify some of the attributes of the quadrilaterals below. Follow these instructions:
- Draw a blue loop around each shape that has 2 pairs of parallel sides.
- Make a red dot inside each shape that has at least 2 right angles.
- Draw a smiley face inside each square.
- Make a green dot inside each shape that has exactly 1 pair of parallel sides.
- Draw an X above each shape that has 4 sides that are exactly the same length.
- Draw a purple loop around each trapezoid.
Answer:
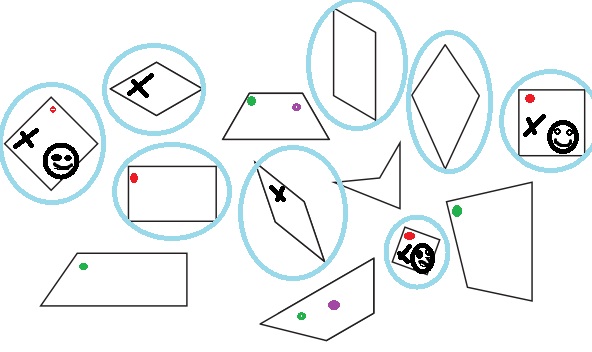
Explanation:
We need to draw a blue loop around each shape that has 2 pair of parallel sides {the shapes are rectangle, square, parallelogram and kite}.
We need to make a red dot inside each shape that has at least 2 right angles {the shapes are square and a rectangle}.
We need to make a smiley inside each square.
We need to make a green dot inside each shape that has exactly 1 pair of parallel sides {the shape is a trapezoid}.
We need to draw an X above each shape that has 4 sides that are exactly the same length {the shape is a square}.
We need to draw a purple loop around each trapezoid.
Question 2.
Multiply.
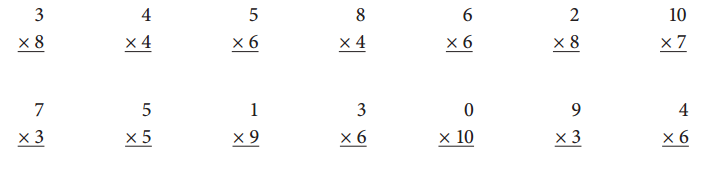
Answer:
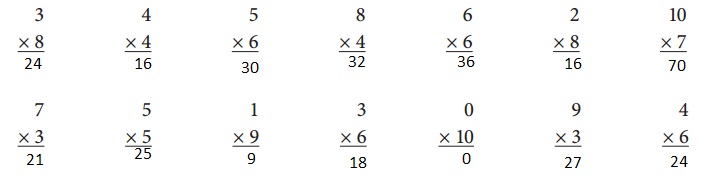
Explanation:
By mental computation,
As the number to be added is 3 and the integral number value is 8, so to find the value we need to add 3 for 8 times, 3 × 8 = 3+3+3+3+3+3+3+3 = 24, hence 3 × 8 = 24.
By mental computation,
As the number to be added is 4 and the integral number value is 4, so to find the value we need to add 4 for 4 times, 4 × 7 = 4 + 4 + 4 + 4 = 16, hence 4 × 4 = 16.
By mental computation,
As the number to be added is 5 and the integral number value is 6, so to find the value we need to add 5 for 6 times, 5 × 6 = 5 + 5 + 5 + 5 + 5 + 5 = 30, hence 5 × 6 =30.
By mental computation,
As the number to be added is 8 and the integral number value is 4, so to find the value we need to add 8 for 4 times, 8 × 4 = 8 + 8 + 8 + 8 = 32, hence 8 × 4 = 32.
By mental computation,
As the number to be added is 6 and the integral number value is 6, so to find the value we need to add 6 for 6 times, 6 × 6 = 6 + 6 + 6 + 6 = 36, hence 6 × 6 = 36.
By mental computation,
As the number to be added is 2 and the integral number value is 8, so to find the value we need to add 2 for 8 times, 2 × 8 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 16, hence 2 × 8 = 16.
By mental computation,
As the number to be added is 10 and the integral number value is 7, so to find the value we need to add 10 for 7 times, 10 × 7 = 10 + 10 + 10 + 10 + 10 + 10 + 10 = 70, hence 10 × 7 = 70.
By mental computation,
As the number to be added is 7 and the integral number value is 3, so to find the value we need to add 7 for 3 times, 7 × 3 = 7 + 7 + 7 = 21, hence 7 × 3 = 21.
By mental computation,
As the number to be added is 5 and the integral number value is 5, so to find the value we need to add 5 for 5 times, 5 × 5 = 5 + 5 + 5 + 5 + 5 = 25, hence 5 × 5 = 25.
By mental computation,
As the number to be added is 1 and the integral number value is 9, so to find the value we need to add 1 for 9 times, 1 × 9 = 1 + 1 + 1 + 1 + 1 + 1 + 1 +1 +1 = 9, hence 1 × 9 = 9.
By mental computation,
As the number to be added is 3 and the integral number value is 6, so to find the value we need to add 3 for 6 times, 3 × 6 = 3 + 3 + 3 + 3 + 3 + 3 = 18, hence 3 × 6 = 18.
By mental computation,
As the number to be added is 0 and the integral number value is 10, so to find the value we need to add 0 for 10 times, 0 × 10 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0+ 0 = 0, hence 0 × 10 = 0.
By mental computation,
As the number to be added is 9 and the integral number value is 3, so to find the value we need to add 9 for 3 times, 9 × 3 = 9 + 9 + 9 = 27, hence 9 × 3 = 27.
By mental computation,
As the number to be added is 4 and the integral number value is 6, so to find the value we need to add 4 for 6 times, 4 × 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24, hence 4 × 6 = 24.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 1 Session 4 Answer Key
Quadrilaterals
Question 1.
Cross out the figure that is not a parallelogram.
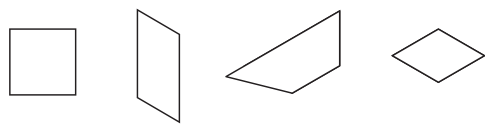
Answer:
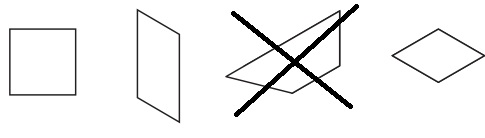
Explanation:
Parallelogram is a quadrilateral in which two pair of opposite sides are parallel.
The crossed out figure is not a parallelogram as only one pair of opposite sides are parallel. Such a quadrilateral is known as trapezoid.
Question 2.
Cross out the figure that is not a trapezoid.
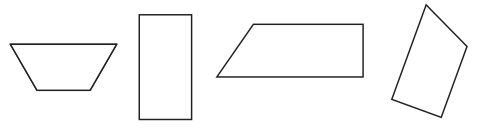
Answer:
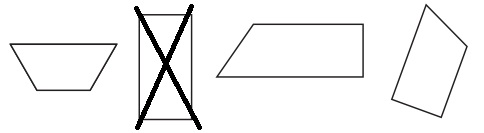
Explanation:
Trapezoid is a quadrilateral in which only one pair of opposite sides are parallel.
The crossed out figure is not a trapezoid as two pairs of opposite sides are parallel. Such a quadrilateral is known as parallelogram.
Question 3.
How is a trapezoid like a parallelogram? Use labeled sketches and words to explain.
Answer:
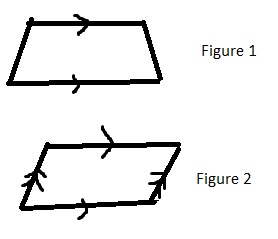
Figure 1 is a trapezoid.
Figure 2 is a parallelogram.
Trapezoid and parallelogram are same because they have parallel lines.
Question 4.
How are a trapezoid and a parallelogram different? Use labeled sketches and words to explain.
Answer:
Figure 1 is a trapezoid.
Figure 2 is a parallelogram.
Trapezoid and parallelogram are different because trapezoid has only one pair of pair lines whereas a parallelogram has two pairs of parallel lines.
Question 5.
Solve the following problems.
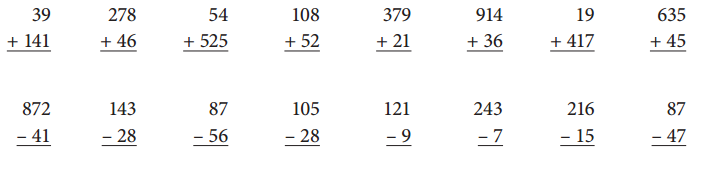
Answer:
Explanation:
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 39+141 = 180.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 278+46 = 324.
.There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 54+525 = 579.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 108+52 = 160.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 379+21 = 400.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 914+36 = 950.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 19+417 = 436.
There are two 3-digit numbers in column form, first add numbers in the ones place, then tens and lastly add numbers in the hundreds place, 635+45 = 680.
Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Rename 4 tens and 3 ones as “3 tens and 13 ones.”
Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Subtract the ones.
Subtract the tens.
Rename 1 hundreds , 0 tens and 5 ones as “0 hundreds , 9 tens and 15 ones.”
Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Rename 1 hundreds , 2 tens and 1 ones as “0 hundreds , 1 tens and 11 ones.”
Subtract the ones.
Subtract the tens.
Subtract the hundreds
Rename 4 tens and 3 ones as “3 tens and 13 ones.”
Subtract the ones.
Subtract the tens.
Subtract the hundreds.
Subtract the ones.
Subtract the tens.
Subtract the hundreds
Subtract the ones.
Subtract the tens.
Bridges in Mathematics Grade 3 Student Book Unit 6 Module 1 Session 5 Answer Key
Work Place Instructions 6A Tangram Polygons
Each pair of players needs:
- one 6A Tangram Polygons Record Sheet to share
- 2 sets of tangrams
- 2 rulers
1. Players decide how many tangram pieces they want to use to build each shape. They write that number on the blank provided on the Tangram Polygons Record Sheet. Players can choose from 3, 4, 5, or 7 pieces. Players have all 7 tangram pieces available to use, but will use only the number chosen to build each polygon. For example, if a player chooses to build with 4 pieces, any 4 pieces from the entire set may be used for each polygon. Players do not have to use the same 4 pieces every time.
2. Players work together to build each of the polygons shown on the record sheet. Many have more than one solution.
Note One shape cannot be made with 5 pieces, and one shape cannot be made with 7 pieces.
3. Players draw a sketch or sketches on the record sheet showing how they built each polygon.
- Players may use a ruler if they need help drawing straight lines.
- Players label the tangram pieces in their sketches with tangram piece letters, so other people can see how they solved the puzzles.
- Players show one or more ways they can find to build a shape.
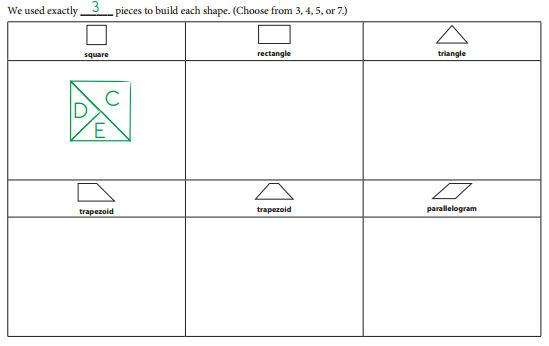
4. Players can come back to this Work Place on other days, each time using a different number of pieces and a new record sheet.
Game Variations
A. Players may choose to work alone at this Work Place.
B. After four visits to this Work Place, students may be interested in seeing what other polygons can be formed with 3, 4, 5, or 7 pieces. A wide variety of irregular polygons are possible. Students could create their own puzzle/record sheets for classmates to solve.
Answer:
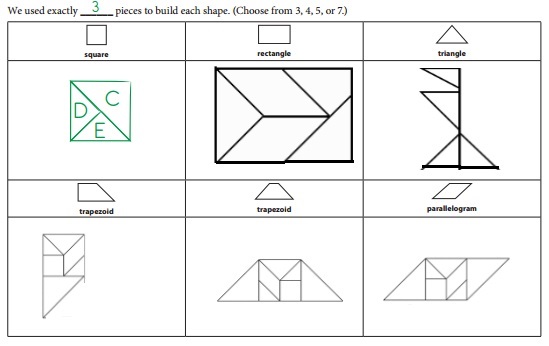
Polygons
Question 1.
Two of the shapes below are polygons, and two are not. a Circle the two polygons.
a. Circle the two polygons.
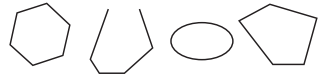
Answer:
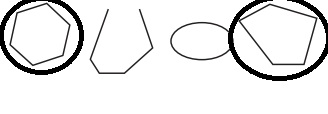
Explanation:
Polygon means a closed with any number of sides.
b. Explain why the other two shapes are not polygons.
Answer:
The other two shapes are not polygons because:
It’s not a closed figure.
Circle is not a polygon because it does not have any sides.
Question 2.
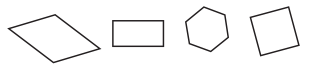
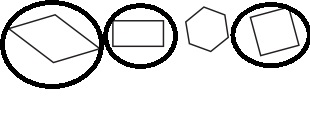
Three of the shapes below are quadrilaterals, and one is not. a Circle the three quadrilaterals.
a. Circle the three quadrilaterals.
Answer:
Explanation:
Quadrilateral means four sided closed figure.
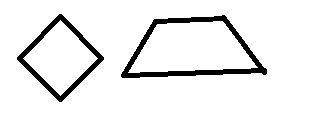
b. Draw two quadrilaterals that are not the same types as those you just circled.
Answer:
Question 3.
Multiply.
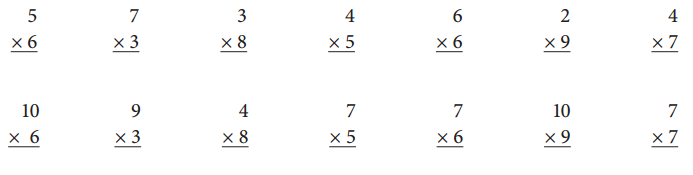
Answer:
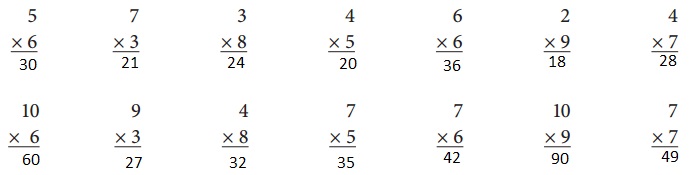
Explanation:
By mental computation,
As the number to be added is 5 and the integral number value is 6, so to find the value we need to add 5 for 6 times, 5 × 6 = 5 + 5 + 5 + 5 + 5 + 5 = 30, hence 5 × 6 = 30.
By mental computation,
As the number to be added is 7 and the integral number value is 3, so to find the value we need to add 7 for 3 times, 7 × 3 = 7 + 7 + 7 = 21, hence 7 × 3 = 21.
By mental computation,
As the number to be added is 3 and the integral number value is 8, so to find the value we need to add 3 for 8 times, 3 × 8 = 3 + 3 + 3 + 3 + 3 + 3 + 3 +3 = 24, hence 3 × 8 = 24.
By mental computation,
As the number to be added is 4 and the integral number value is 5, so to find the value we need to add 4 for 5 times, 4 × 5 = 4 + 4 + 4 + 4 + 4 = 20, hence 4 × 5 = 20.
By mental computation,
As the number to be added is 6 and the integral number value is 6, so to find the value we need to add 6 for 6 times, 6 × 6 = 6 + 6 + 6 + 6 + 6 + 6 = 36, hence 6 × 6 = 36.
By mental computation,
As the number to be added is 2 and the integral number value is 9, so to find the value we need to add 2 for 9 times, 2 × 9 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18, hence 2 × 9 = 18.
By mental computation,
As the number to be added is 4 and the integral number value is 7, so to find the value we need to add 4 for 7 times, 4 × 7 = 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28, hence 4 × 7 = 28.
Step 1: Multiply the integral value 6 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 6 × 0 = 0.
Step 2: Multiply the integral value 6 with the number in tens place, any number multiplied by 1 gives the same number itself, hence 6 × 1 = 6.
Therefore, 10 × 6 = 60.
By mental computation,
As the number to be added is 9 and the integral number value is 3, so to find the value we need to add 9 for 3 times, 9 × 3 = 9 + 9 + 9 = 27, hence 9 × 3 = 27.
By mental computation,
As the number to be added is 4 and the integral number value is 8, so to find the value we need to add 4 for 8 times, 4 × 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32, hence 4 × 8 = 32.
By mental computation,
As the number to be added is 7 and the integral number value is 5, so to find the value we need to add 7 for 5 times, 7 × 3 = 7 + 7 + 7 + 7 + 7 = 35, hence 7 × 5 = 35.
By mental computation,
As the number to be added is 7 and the integral number value is 6, so to find the value we need to add 7 for 6 times, 7 × 3 = 7 + 7 + 7 + 7 + 7 + 7 = 42, hence 7 × 6 = 42.
Step 1: Multiply the integral value 9 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 9 × 0 = 0.
Step 2: Multiply the integral value 9 with the number in tens place, any number multiplied by 1 gives the same number itself, hence 9 × 1 = 9.
Therefore, 10 × 9 = 90.
By mental computation,
As the number to be added is 7 and the integral number value is 7, so to find the value we need to add 7 for 7 times, 7 × 3 = 7 + 7 + 7 + 7 + 7 + 7 + 7 = 49, hence 7 × 7 = 49.
Question 4.
CHALLENGE Multiply.
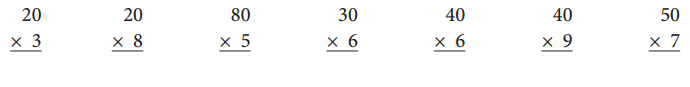
Answer:
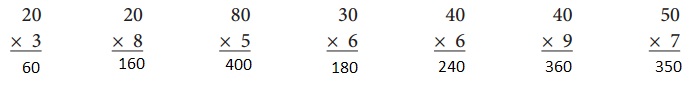
Explanation:
Step 1: Multiply the integral value 3 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 3 × 0 = 0.
Step 2: Multiply the integral value 3 with the number in tens place, hence 3 × 2 = 6.
Therefore, 20 × 3 = 60.
Step 1: Multiply the integral value 8 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 8 × 0 = 0.
Step 2: Multiply the integral value 8 with the number in tens place, hence 8 × 2 = 16.
Therefore, 20 × 8 = 160.
Step 1: Multiply the integral value 5 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 5 × 0 = 0.
Step 2: Multiply the integral value 5 with the number in tens place hence 5 × 8 = 40.
Therefore, 80 × 5 = 400.
Step 1: Multiply the integral value 6 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 6 × 0 = 0.
Step 2: Multiply the integral value 6 with the number in tens place hence 6 × 3 = 18.
Therefore, 30 × 6 = 180.
Step 1: Multiply the integral value 6 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 6 × 0 = 0.
Step 2: Multiply the integral value 6 with the number in tens place hence 6 × 4 = 24.
Therefore, 40 × 6 = 240.
Step 1: Multiply the integral value 9 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 9 × 0 = 0.
Step 2: Multiply the integral value 9 with the number in tens place hence 9 × 4 = 36.
Therefore, 40 × 9 = 360.
Step 1: Multiply the integral value 7 with the number in ones place, any number multiplied by 0 gives the product as 0, hence 7 × 0 = 0.
Step 2: Multiply the integral value 7 with the number in tens place hence 7 × 5 = 35.
Therefore, 50 × 7 = 350.