The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 3 Module 4 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 3 Module 4
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 4 Session 1 Answer Key
Round, Estimate & Find the Sum
Before you start adding numbers, it is a good idea to estimate what their sum will be. That way, you can tell if your final answer is reasonable. Round each pair of numbers to the nearest ten and then add the rounded numbers to estimate the sum. Then use the standard algorithm to find the exact sum.

Question 1.
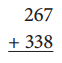
Round, Add & Estimate
The sum will be about _____
Exact sum
(Use the algorithm)
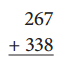
Answer:
First Round both the given numbers ,Then estimate the given by adding them and get the result as 610. Also, find out the Exact sum of the actual given two numbers using the algorithm as 605.
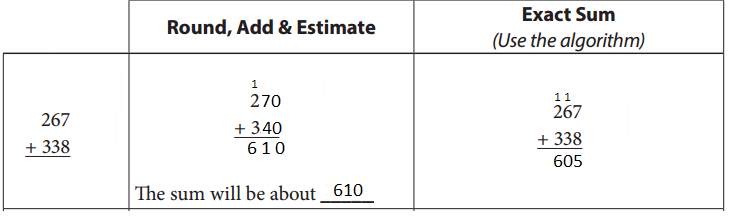
Question 2.

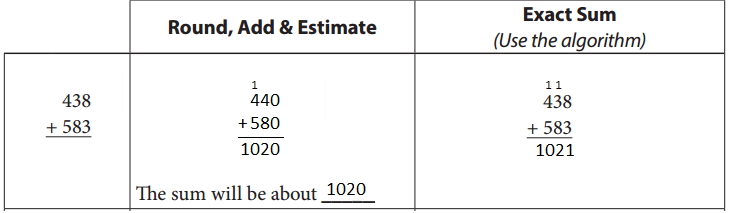
Round, Add & Estimate
The sum will be about _____
Exact sum
(Use the algorithm)

Answer:
First Round both the given numbers ,Then estimate the given by adding them and get the result as 1020. Also, find out the Exact sum of the actual given two numbers using the algorithm as 1021.
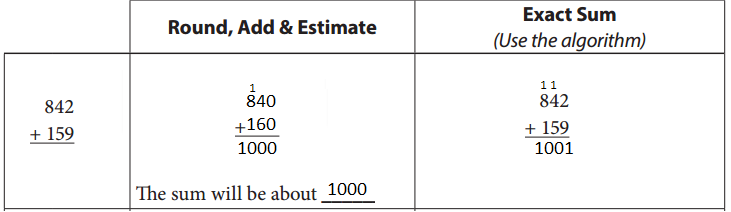
Question 3.
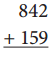
Round, Add & Estimate
The sum will be about _____
Exact sum
(Use the algorithm)
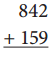
Answer:
First Round both the given numbers ,Then estimate the given by adding them and get the result as 1000. Also, find out the Exact sum of the actual given two numbers using the algorithm as 1001.
Question 4.
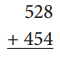
Round, Add & Estimate
The sum will be about _____
Exact sum
(Use the algorithm)
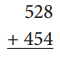
Answer:
First Round both the given numbers ,Then estimate the given by adding them and get the result as 980. Also, find out the Exact sum of the actual given two numbers using the algorithm as 982.
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 4 Session 2 Answer Key
Addition Methods
Use the standard algorithm to solve each problem. Then solve it a different way. Label your method. Circle the strategy that seemed quicker and easier.
ex

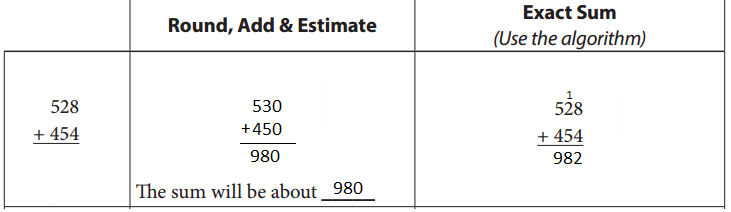
Question 1.
51 + 29 =
Standard Algorithm
Different Strategy
Strategy: ___________
Answer:
First add both the given numbers 51 , 29 and get the result as 90. Then, write the result with a different strategy.
Question 2.
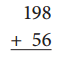
Standard Algorithm
Different Strategy
Strategy: ___________
Answer:
First add both the given numbers 198, 56 and get the result as 254. Then, write the result with a different strategy.

Question 3.
348 + 578 =
Standard Algorithm
Different Strategy
Strategy: ___________
Answer:
First add both the given numbers 348, 578 and get the result as 926. Then, write the result with a different strategy.

Question 4.
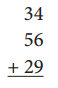
Standard Algorithm
Different Strategy
Strategy: ___________
Answer:
First add both the given numbers 34 , 56 and 72 and get the result as 119. Then, write the result with a different strategy.

More Addition Strategies
Use the standard algorithm to solve each problem. Then solve it a different way. Label your method. Circle the strategy that seemed quicker and easier.
a.
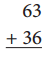
Standard Algorithm
Different Strategy
Strategy: ______
Answer:
First add both the given numbers 63 ,36 and get the result as 99. Then, write the result with a different strategy.

b.
149 + 253
Standard Algorithm
Different Strategy
Strategy: ______
Answer:
First add both the given numbers 149 , 253 and get the result as 402. Then, write the result with a different strategy.

c.
53 + 28 + 72 =
Standard Algorithm
Different Strategy
Strategy: ______
Answer:
First add both the given numbers 53,28 ,72 and get the result as 153. Then, write the result with a different strategy.

d.
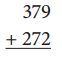
Standard Algorithm
Different Strategy
Strategy: ______
Answer:
First add both the given numbers 379 , 272 and get the result as 651. Then, write the result with a different strategy.

e.
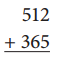
Standard Algorithm
Different Strategy
Strategy: ______
Answer:
First add both the given numbers 512 and 365 and get the result as 877. Then, write the result with a different strategy.

Bridges in Mathematics Grade 3 Student Book Unit 3 Module 4 Session 3 Answer Key
Running Robots
Question 1.
Fill in the bubble to show the best estimate for each problem:
a.
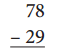
![]() 30
30
![]() 40
40
![]() 50
50
![]() 60
60
Answer:
First round the both numbers , then subtract the 30 from 80 and get the result 50 which is as shown below.

b.
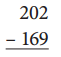
![]() 30
30
![]() 40
40
![]() 50
50
![]() 60
60
Answer:
First round the both numbers , then subtract the 170 from 200 and get the result 30 which is as shown below.
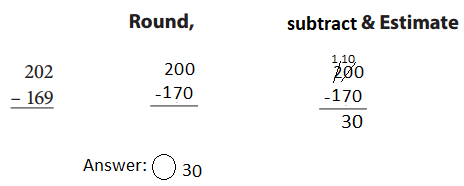
Question 2.
Solve each subtraction problem below. You may use the regrouping strategy (standard algorithm) or any other strategy for addition that is efficient for you. Be sure to show your work.
a. Nina and Ricardo designed robots. Nina’s robot can run for 235 minutes before the batteries need to be recharged. Ricardo’s robot can run for 187 minutes before the batteries need recharging. How much longer can Nina’s robot run than Ricardo’s?
Answer:
Number of minutes that Ricardo’s robot can run = 187
Number of minutes that Nina’s robot can run = 235
Number of minutes that Nina’s robot can run than Ricardo’s = ?
= 235 – 187
= 48 minutes.
b. Kiran and Brenda also designed robots. Kiran’s robot can walk 307 meters before the batteries need to be recharged. Brenda’s robot can walk 268 meters before the batteries need to be recharged. How much farther can Kiran’s robot walk than Brenda’s?
Answer:
Number of minutes taken for design the Robot for Kiran = 307
Number of minutes taken for design the Robot for Brenda’s = 268
Number of minutes taken for Kiran than Brenda’s = ?
= 307 – 268
= 39 minutes.
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 4 Session 4 Answer Key
Subtraction Strategies
Use the standard algorithm to solve each problem. Then solve it a different way. Label your method. Circle the strategy that seemed quicker and easier.
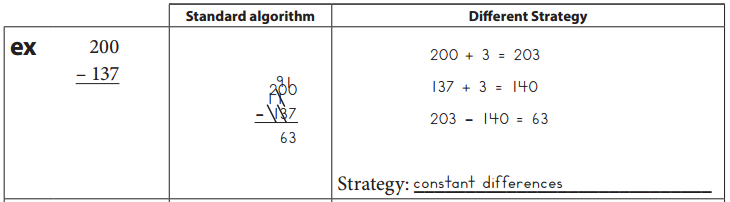
Question 1.
75 – 24 =
Standard algorithm
Different Strategy
Strategy: _________
Answer:
First subtract the given numbers 24 from 75 and get the result as 51.Then , write the given number with a different strategy as shown below.

Question 2.
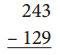
Standard algorithm
Different Strategy
Strategy: _________
Answer:
First subtract the given numbers 129 from 243 and get the result as 114. Then , write the given number with a different strategy as shown below.

Question 3.
512 – 339 =
Standard algorithm
Different Strategy
Strategy: _________
Answer:
First subtract the given numbers 339 from 512 and get the result as 173. Then , write the given number with a different strategy as shown below.

Question 4.
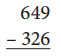
Standard algorithm
Different Strategy
Strategy: _________
Answer:
First subtract the given numbers 326 from 649 and get the result as 323. Then , write the given number with a different strategy as shown below.

More Subtraction Strategies
Use the standard algorithm to solve each problem. Then solve it a different way. Label your method. Circle the strategy that seemed quicker and easier.
Question 1.
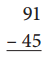
Standard algorithm
Different Strategy
Strategy: ________
Answer:
First subtract the given numbers 45 from 91 and get the result as 46. Then , write the given number with a different strategy as shown below.

Question 2.
253 – 149
Standard algorithm
Different Strategy
Strategy: ________
Answer:
First subtract the given numbers 149 from 253 and get the result as 104. Then , write the given number with a different strategy as shown below.

Question 3.
265 – 174
Standard algorithm
Different Strategy
Strategy: ________
Answer:
First subtract the given numbers 174 from 265 and get the result as 91. Then , write the given number with a different strategy as shown below.

Question 4.
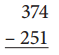
Standard algorithm
Different Strategy
Strategy: ________
Answer:
First subtract the given numbers 251 from 374 and get the result as 123. Then , write the given number with a different strategy as shown below.
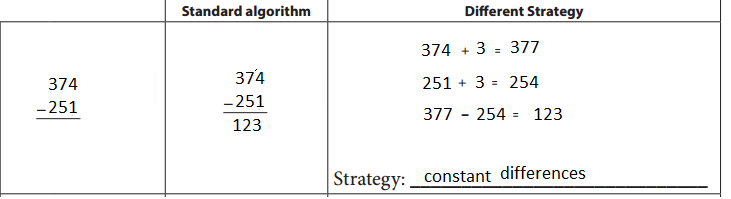
Question 5.
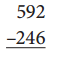
Standard algorithm
Different Strategy
Strategy: ________
Answer:
First subtract the given numbers 346 from 592 and get the result as 346. Then , write the given number with a different strategy as shown below.
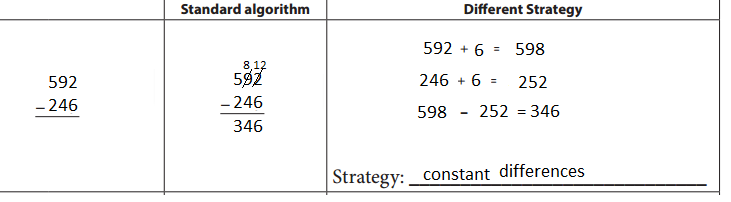
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 4 Session 5 Answer Key
Bike-a-thon
Akira and Taro are participating in a bike-a-thon to raise money for people who lost their homes in an earthquake. For every mile they ride, they will earn $1 to help rebuild and refurnish homes. Show your work with numbers, sketches, or words as you help Akira and Taro figure out how far they have ridden and how much money they have earned. Then, write an equation for each problem.
Question 1.
In one week, Akira rode her bike 87 miles. Taro rode his bike 51 miles. How many more miles did Akira ride?
Equation: ___________________
Answer:
Number of miles rode by Akira = 87 miles
Number of miles rode by Taro = 51 miles
Number of more miles ride by Akira = x = ?
Equation : x = 87 – 51
= 36 miles
Question 2.
After two weeks, Akira and Taro biked a total 276 miles. After 3 weeks, they had biked a total of 413 miles. How many miles did they ride in the third week? (Hint: How much farther had they biked at the end of the third week than at the end of the second week?)
Equation: _______________________
Answer:
Number of miles biked by Akira and taro after 2 weeks = 276
Number of miles biked by Akira and taro after 3 weeks = 413
Number of miles biked by both at the end of 3 week than end of second week = x = ?
Equation : x = 413 – 276
x = 137
Question 3.
Akira and Taro want to raise $537. After four weeks, they have raised $498. How much more money do they need to earn?
Equation: _____________________________
Answer:
Amount of money wants to raise by both Akira and Taro = $537
Amount of money raised after 4 weeks = $ 498
Amount of money both needed to earn = x = ?
Equation : x = 537 – 498
= $ 39