The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 3 Module 1 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 3 Module 1
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 1 Answer Key
Multiplication & Division Fact Families
The fact family that belongs with each array is missing an equation. Write the missing equation for each fact family.
ex
3 × 4 = 12
4 × 3 = 12
12 ÷ 3 = 4
12 ÷ 4 = 3
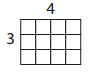
a.
10 × 3 = 30
____ × ____ = _____
30 ÷ 3 = 10
30 ÷ 10 = 3
Answer:
Number of rows = 3
Number of columns = 10
The missing Equation for the given fact family is 3 x 10 = 30.
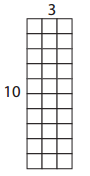
b.
2 × 9 = 18
____ × ____ = _____
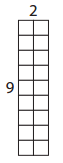
18 ÷ 2 = 9
18 ÷ 9 = 2
Answer:
Number of rows = 2
Number of columns = 9
The missing Equation for the given fact family is 9 x 2 = 18.
c.
5 × 8 = 40
8 × 5 = 40
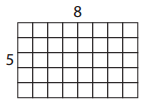
____ ÷ _____ = _____
40 ÷ 8 = 5
Answer:
Number of rows = 5
Number of columns = 8
The missing Equation for the given fact family is 40 ÷ 5 = 8.
Question 2.
Fill in the missing number in each triangle and then write the fact family.
ex
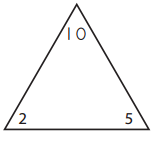
2 × 5 = 10
5 × 2 = 10
10 ÷ 2 = 5
10 ÷ 5 = 2
a.
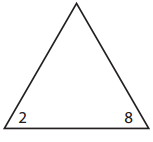
____ × ____ = _____
____ × _____ = _____
____ ÷ _____ = _____
____ ÷ _____ = ______
Answer:
Here, The missing number for the given triangle is 16 and the facts are written as shown below.
2 x 8 = 16
8 x 2 = 16
16 ÷ 8 = 2
16 ÷ 2 = 8
b.
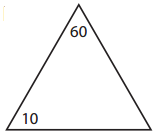
____ × ____ = _____
____ × _____ = _____
____ ÷ _____ = _____
____ ÷ _____ = ______
Answer:
The missing number for the given triangle is 6 and the facts are written as shown below.
10 x 6 = 60
6 x 10 = 60
60 ÷ 10 =6
60 ÷ 6 = 10
c.
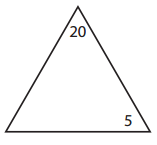
____ × ____ = _____
____ × _____ = _____
____ ÷ _____ = _____
____ ÷ _____ = ______
Answer:
The missing number for the given triangle is 4 and the facts are written as shown below.
4 x 5 = 20
5 x 4 = 20
20 ÷ 5 = 4
20 ÷ 4 = 5
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 2 Answer Key
Work Place Instructions 3A Round Ball Tens
Each pair of players needs:
- 1 Round Ball Tens Record Sheet to share
- 1 spinner overlay
- scratch paper
1. Player 1 spins each spinner and writes the two numbers on a sheet of scratch paper. If the arrow lands on the line, he spins again.
2. Player 1 decides which number to use in the tens place and which number to use in the ones place.
In the example below, 4 and 6 could be used to make 46 or 64.
- 46 rounds to 50
- 64 rounds to 60
In this example, 64 was chosen, so 64 was recorded in the basket marked 60.
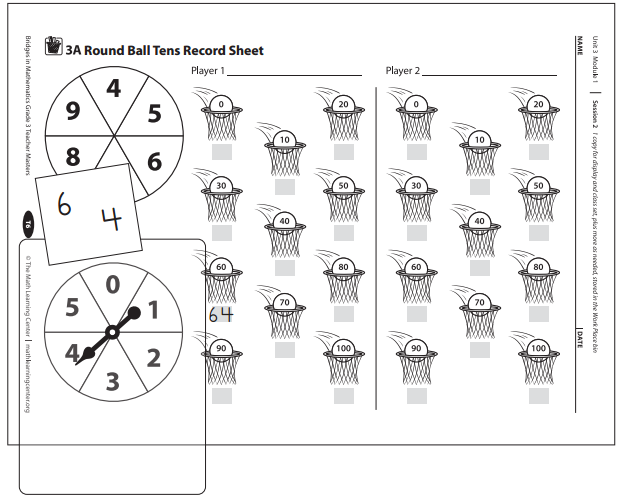
3. Players continue taking turns spinning both spinners and deciding how to arrange the two numbers.
If both baskets for the numbers spun already have numbers in them, players can write the number they choose next to one of the baskets.
4. The first player to get at least one number in each basket wins. If players run out of time, the player with numbers in the most baskets wins the game.
Game Variation
A. Players can put only one number in or near a basket. If they cannot put either of their numbers in a basket, they lose their turn.
Write & Solve Your Own Problems
Fill in the blanks with words that make sense and seem interesting. Solve each problem. Show your work.
Question 1.
Sara has 35 ____ in her top drawer. She has 28 ___ in her bottom drawer. How many are there in all? ____
Work space
Answer:
Number in top drawer = 35
Number in top drawer = 28
Number there in all = ?
= 35 + 26
= 61
Question 2.
Tim spent 26 dollars for a ____. He spent 18 dollars for a ____. How much did he spend in all? ____
Work space
Answer:
Initially spent = 26
Later spent = 18
Spent in all = ?
= 26 + 18
= 44
Question 3.
Isabel had 74 ____. She gave 26 of them to a friend. How many did she have left? _____
Work space
Answer:
Total present with Isabel = 74
Given for a friend = 26
Number left with her = ?
= 74 – 26
= 48
Question 4.
Juan baked 4 dozen ____. The dog ate 19 of them. How many are left? ________
Work space
Answer:
Number baked by john = 4 dozen = 4 x 12 = 48
Number ate by dog = 19
Number of left = ?
= 48 – 19
= 29
Question 5.
We saw 102 ________. Then 24 of them flew away. How many were left? _______
Work space
Answer:
Number of seen = 102
Number that flew away = 24
Number of left = ?
= 102 – 24
= 78
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 3 Answer Key
Work Place Instructions 3B Round & Add Tens
Each pair of players needs:
- a record sheet
- a spinner overlay
1. Players decide who will who will spin and who will record the numbers. Players switch roles for each turn.
2. Players spin the spinner 4 times to fill in 4 digits on the record sheet.

3. Players work together to round each number formed to the nearest 10 and fill in the blanks under Sum of Rounded Numbers.

4. Players work together to find the sum of the actual numbers and the sum of the rounded numbers.
5. Players’ score is the difference between the sum of the actual numbers and the sum of the rounded numbers.

6. Players continue spinning, rounding, and adding until they have played all 5 rounds of the game. Then they add their scores from each round to get their final score.
Note: Players can work together to play the game a second time and see if they can get a lower score.
Game Variations
A. Students can each use their own record sheet and take turns, each spinning and recording for themselves. Low score wins the game.
B. Instead of recording the numbers in order as they spin, players can spin all 4 numbers and then use the digits to form the two 2-digit numbers that will yield the lowest score.
Adding & Rounding
Question 1.
Solve each problem below. Show your work.

Answer:
Add the given following combinations and get the result as shown below.

Question 2.
Akiko wants to add 98 and 43. What is an easy way for Akiko to add these two numbers? Solve the problem and show your work.
Answer:
First Add the numbers 8 and 3 in ones place and get the result as 11.Then , place 1 on top of the number 9 which is in tens place. Again, add the numbers in tens place and add 1. Then the overall result is 141.
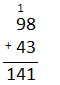
Question 3.
Jamal is playing Add & Round Tens with a partner. He got a 2, an 8, a 3, and a 7 on his first turn. He wrote them down as he spun them, and wound up with 28 + 37.
a. What are his rounded numbers? ___ and _____
Answer:
Given numbers 28 and 37.
when they are rounded 28 becomes 30 and 37 becomes 40.
Therefore the numbers are 30 and 40.
b. What is the sum of his rounded numbers? ______
Answer:
The rounded numbers are 30 and 40.
Then the sum of rounded numbers = 30 + 40 = 70.
c. What is the sum of his actual numbers? Show your work.
Answer:
The actual numbers are 28 and 37.
When both are added : 28 + 37 = 65
d. What is the difference between the sum of his rounded numbers and the sum of his actual numbers? Show your work.
Answer:
Sum of rounded numbers = 70
Sum of actual numbers = 65
Difference = 70 – 65
= 5
Question 4.
CHALLENGE The next time they played Add & Round Tens, Jamal and his partner decided to change the rules so they can arrange the numbers they spin to make any 2-digit numbers they want. Oh his first turn, Jamal got these four numbers: 2, 4, 7, and 1. Arrange these numbers to get the lowest score possible. (Remember that your score is the difference between the sum of the actual numbers and the sum of the rounded numbers.)
Answer:
Let the numbers be 24 and 71
When they are rounded ; 24 = 20 and 71 = 70.
Then, sum of rounded numbers = 20 + 70
= 90
Actual numbers are 24 and 71
When both are added = 24 + 71
= 95
Difference = 95 – 90
= 5
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 4 Answer Key
Work Place Instructions 3C Round Ball Hundreds
Each pair of players needs:
- 1 Round Ball Hundreds Record Sheet to share
- 1 deck of Number Cards with 0s, 1s, and wild cards removed
- scratch paper
1. Players shuffle the remaining cards in the deck and place them face-down in a stack.
2. Player 1 draws 3 cards off the top of the deck and arranges them to make a 3-digit number. She rounds them to the nearest hundred and records the 3-digit number she made in the appropriate basket.
In the example below, 8, 4, and 6 have been used to make 846. Rounded to the nearest 100, it would be 800, so 846 is recorded in the basket marked 800.
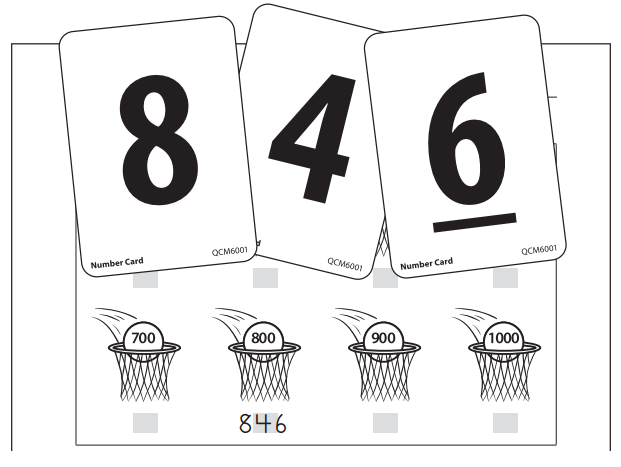
3. Player 1 puts the used cards in a discard pile and Player 2 draws 3 new cards, arranges them, rounds the number to the nearest hundred, and records this number in the appropriate basket.
4. Players continue taking turns. They draw 3 cards each time, decide how to arrange the numbers, and round the 3-digit number to determine which basket gets the number.
- If no empty hoops are available for the three possible arrangements of the numbers a player draws, the player misses that turn.
- If players play through the deck, they shuffle the cards and continue playing.
5. The first player to get a number in every basket wins the game.
6. When putting the number cards away, players should be sure to return the 0s, 1s, and wild cards to the deck.
Game Variation
A. Play Round Ball Thousands. Write another zero at the end of each number on each basketball hoop. Then, draw 4 cards, arrange them as a 4-digit number, round the number to the nearest 1,000, and determine which basket gets the number.
Rounding
Question 1.
Round these numbers to the nearest ten.
26 → 73 → 148 → 57 → 261 →
82 → 35 → 912 → 2,179 → 444 →
Answer:
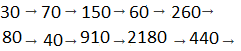
Question 2.
Round these numbers to the nearest hundred.
360 → 452 → 720 → 112 → 680 →
1,241 → 870 → 2,550 → 327 → 5,173 →
Answer:
For rounding the given number to the nearest hundreds , First observe the number at hundreds place. (i).If the number is 5 or more than 5 , Simply round up the number.(ii).if the number is less than 5 , Simply round down the number.
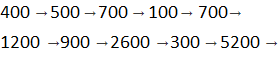
Question 3.
Round these numbers.
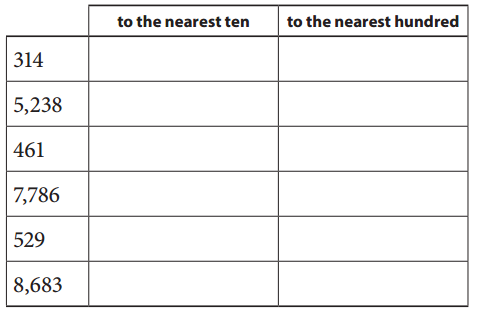
Answer:
1). For rounding the given number to the nearest tens , First observe the number at tens place.(i).If the number is 5 or more than 5 , Simply round up the number.(ii).if the number is less than 5 , Simply round down the number.
2). For rounding the given number to the nearest hundreds , First observe the number at hundreds place.(i).If the number is 5 or more than 5 , Simply round up the number.(ii).if the number is less than 5 , Simply round down the number.
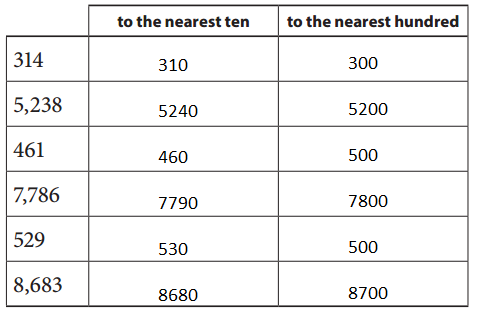
Question 4.
Solve the following problems.
7 × 6 = _____ ____ × 6 = 24 9 × ____ = 63
2 × 9 = 3 × ____ 2 × 8 = _____ 6 × ____ = 3 × 10
Answer:
missing numbers for the given blanks are as shown below.
7 × 6 = 42 4 × 6 = 24 9 × 7 = 63
2 × 9 = 3 × 6 2 × 8 = 16 6 × 5 = 3 × 10
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 5 Answer Key
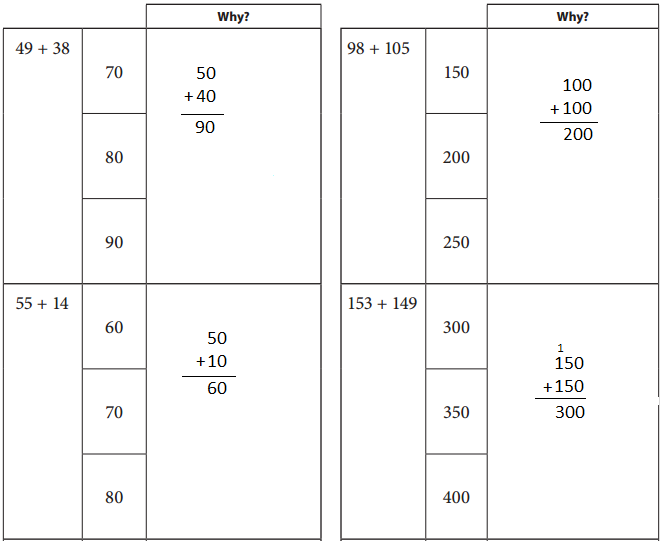
Which Makes the Most Sense?
Choose the best estimate for each problem and explain your thinking. Hint: use rounding to help.
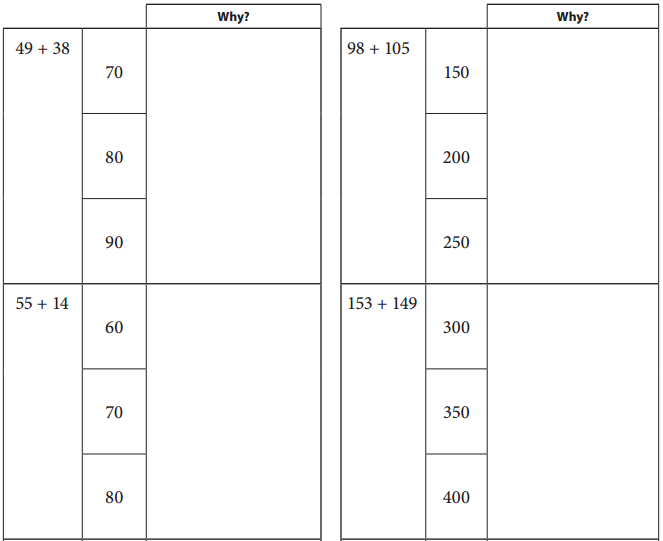

Answer:
First round the given actual numbers and get the respective results after rounding which are as shown below.
Bridges in Mathematics Grade 3 Student Book Unit 3 Module 1 Session 6 Answer Key
Strategy Match 3
Three students solved the problem 243 + 187. All the students used a number line, but each student solved the problem differently. Match the students’ work below to the strategies in the table.

Question 1.
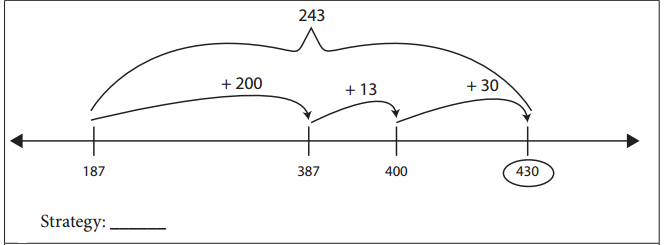
Answer:
Strategy : 187 + 243 = 430
The above strategy is used by adding a friendly number which is very big and went back for the Given number Line.
Question 2.
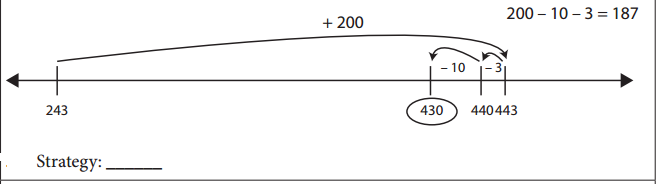
Answer:
Strategy :
243 + 200 – 10 – 3 = 430.
The above strategy is used by adding a friendly number , going back to a friendly number and adding the remaining in the Given number Line.
Question 3.
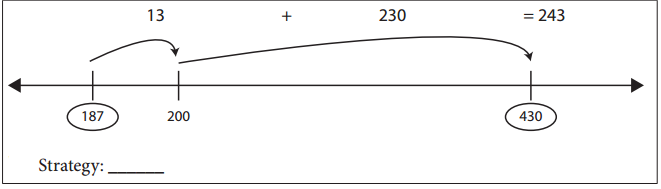
Answer:
Strategy : 187 + 13 + 230 = 430
The above strategy is used where the number is friendly right away and adding a friendly number and adding the remaining in the Given number Line.