Trying to Score Better Scores in Grade 5 Maths? Utilize Big Ideas Math Answers Grade 5 Chapter 9 Multiply Fractions and make the most out of them. Begin your practice right away using the Big Ideas Math Answers Grade 5 Chapter 9 Multiply Fractions and understand the concepts. Attain more knowledge using the Big Ideas Math Book 5th Grade Answer Key Chapter 9 Multiply Fractions and cross-check the Solutions from it after your practice sessions.
Big Ideas Math Book 5th Grade Answer Key Chapter 9 Multiply Fractions
Apply Maths in your Real-Time and get the Tips & Tricks to Solve Various Problems using Big Ideas Math Book 5th Grade Answer Key Chapter 9 Multiply Fractions. Try to utilize the resource available Big Ideas Math Answers Grade 5 Chapter 9 Multiply Fractions and make your preparation way more effective. You just need to tap on the quick links available in order to access them and learn all the topics.
Lesson: 1 Multiply Whole Numbers by Fractions
- Lesson 9.1 Multiply Whole Numbers by Fractions
- Multiply Whole Numbers by Fractions Homework & Practice 9.1
Lesson: 2 Use Models to Multiply Fractions by Whole Numbers
- Lesson 9.2 Use Models to Multiply Fractions by Whole Numbers
- Use Models to Multiply Fractions by Whole Numbers Homework & Practice 9.2
Lesson: 3 Multiply Fractions and Whole Numbers
- Lesson 9.3 Multiply Fractions and Whole Numbers
- Multiply Fractions and Whole Numbers Homework & Practice 9.3
Lesson: 4 Use Models to Multiply Fractions
- Lesson 9.4 Use Models to Multiply Fractions
- Use Models to Multiply Fractions Homework & Practice 9.4
Lesson: 5 Multiply Fractions
Lesson: 6 Find Areas of Rectangles
Lesson: 7 Multiply Mixed Numbers
Lesson: 8 Compare Factors and Products
Chapter: 9 – Multiply Fractions
Lesson 9.1 Multiply Whole Numbers by Fractions
Explore and Grow
Write any proper fraction that is not a unit fraction. Draw a model to represent your fraction. Draw a model to find a multiple of your fraction?
Answer:
The proper fraction that is not a unit fraction is: \(\frac{5}{8}\)
Let the proper fraction be multiplied by 5
So,
We have to find the value of 5 × \(\frac{5}{8}\)
Now,
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
5 × \(\frac{5}{8}\)
= \(\frac{5}{1}\) × \(\frac{5}{8}\)
= \(\frac{5 × 5}{1 × 8}\)
= \(\frac{25}{8}\)
Hence, from the above,
We can conclude that the multiple of your proper fraction is: \(\frac{25}{8}\)
Reasoning
How can you use a model to multiply a whole number by a fraction? Explain.
Answer:
We can multiply a whole number by a fraction using the properties of multiplication. They are:
A) a = \(\frac{a}{1}\)
B) a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
Hence, by using the above properties, we can multiply the whole number by a fraction.
Think and Grow: Multiply Whole Numbers by Fractions
Example
Find 3 × \(\frac{2}{5}\)
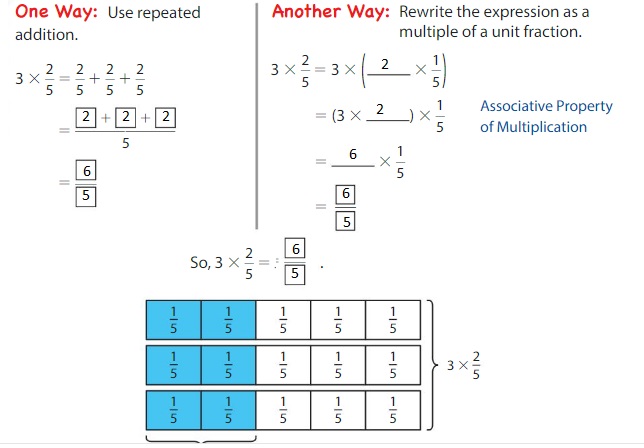
Show and Grow
Multiply.
Question 1.
2 × \(\frac{3}{4}\) = ______
Answer:
2 × \(\frac{3}{4}\) = \(\frac{6}{4}\)
Explanation:
The given numbers are: 2 and \(\frac{3}{4}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
2 × \(\frac{3}{4}\)
= \(\frac{2}{1}\) × \(\frac{3}{4}\)
= \(\frac{2 × 3}{1 × 4}\)
= \(\frac{6}{4}\)
Hence,
2 × \(\frac{3}{4}\) = \(\frac{6}{4}\)
Question 2.
4 × \(\frac{5}{8}\) = ____
Answer:
4 × \(\frac{5}{8}\) = \(\frac{20}{8}\)
Explanation:
The given numbers are: 4 and \(\frac{5}{8}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
4 × \(\frac{5}{8}\)
= \(\frac{4}{1}\) × \(\frac{5}{8}\)
= \(\frac{4 × 5}{1 × 8}\)
= \(\frac{20}{8}\)
Hence,
4 × \(\frac{5}{8}\) = \(\frac{20}{8}\)
Apply and Grow: Practice
Multiply.
Question 3.
5 × \(\frac{7}{10}\) = ______
Answer:
5 × \(\frac{7}{10}\) = \(\frac{35}{10}\)
Explanation:
The given numbers are: 5 and \(\frac{7}{10}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
5 × \(\frac{7}{10}\)
= \(\frac{5}{1}\) × \(\frac{7}{10}\)
= \(\frac{5 × 7}{1 × 10}\)
= \(\frac{35}{10}\)
Hence,
5 × \(\frac{7}{10}\) = \(\frac{35}{10}\)
Question 4.
8 × \(\frac{2}{3}\) = ______
Answer:
8 × \(\frac{2}{3}\) = \(\frac{16}{3}\)
Explanation:
The given numbers are: 8 and \(\frac{2}{3}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
8 × \(\frac{2}{3}\)
= \(\frac{8}{1}\) × \(\frac{2}{3}\)
= \(\frac{8 × 2}{1 × 3}\)
= \(\frac{16}{3}\)
Hence,
8 × \(\frac{2}{3}\) = \(\frac{16}{3}\)
Question 5.
7 × \(\frac{5}{6}\) = ______
Answer:
7 × \(\frac{5}{6}\) = \(\frac{35}{6}\)
Explanation:
The given numbers are: 7 and \(\frac{5}{6}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
7 × \(\frac{5}{6}\)
= \(\frac{7}{1}\) × \(\frac{5}{6}\)
= \(\frac{7 × 5}{1 × 6}\)
= \(\frac{35}{6}\)
Hence,
7 × \(\frac{5}{6}\) = \(\frac{35}{6}\)
Question 6.
9 × \(\frac{1}{2}\) = ______
Answer:
9 × \(\frac{1}{2}\) = \(\frac{9}{2}\)
Explanation:
The given numbers are: 9 and \(\frac{1}{2}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
9 × \(\frac{1}{2}\)
= \(\frac{9}{1}\) × \(\frac{1}{2}\)
= \(\frac{9 × 1}{1 × 2}\)
= \(\frac{9}{2}\)
Hence,
9 × \(\frac{1}{2}\) = \(\frac{9}{2}\)
Question 7.
6 × \(\frac{3}{100}\) = ______
Answer:
6 × \(\frac{3}{100}\) = \(\frac{18}{100}\)
Explanation:
The given numbers are: 6 and \(\frac{3}{100}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
6 × \(\frac{3}{100}\)
= \(\frac{6}{1}\) × \(\frac{3}{100}\)
= \(\frac{6 × 3}{1 × 100}\)
= \(\frac{18}{100}\)
Hence,
6 × \(\frac{3}{100}\) = \(\frac{18}{100}\)
Question 8.
15 × \(\frac{4}{7}\) = ______
Answer:
15 × \(\frac{4}{7}\) = \(\frac{60}{7}\)
Explanation:
The given numbers are: 15 and \(\frac{4}{7}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
15 × \(\frac{4}{7}\)
= \(\frac{15}{1}\) × \(\frac{4}{7}\)
= \(\frac{15 × 4}{1 × 7}\)
= \(\frac{60}{7}\)
Hence,
15 × \(\frac{4}{7}\) = \(\frac{60}{7}\)
Question 9.
10 × \(\frac{5}{3}\) = ______
Answer:
10 × \(\frac{5}{3}\) = \(\frac{50}{3}\)
Explanation:
The given numbers are: 10 and \(\frac{5}{3}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
10 × \(\frac{5}{3}\)
= \(\frac{10}{1}\) × \(\frac{5}{3}\)
= \(\frac{10 × 5}{1 × 3}\)
= \(\frac{50}{3}\)
Hence,
10 × \(\frac{5}{3}\) = \(\frac{50}{3}\)
Question 10.
4 × \(\frac{5}{2}\) = ______
Answer:
4 × \(\frac{5}{2}\) = 10
Explanation:
The given numbers are: 4 and \(\frac{5}{2}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
4 × \(\frac{5}{2}\)
= \(\frac{4}{1}\) × \(\frac{5}{2}\)
= \(\frac{4 × 5}{1 × 2}\)
= \(\frac{20}{2}\)
= 10
Hence,
4 × \(\frac{5}{2}\) = 10
Question 11.
3 × \(\frac{11}{8}\) = ______
Answer:
3 × \(\frac{11}{8}\) = \(\frac{33}{8}\)
Explanation:
The given numbers are: 3 and \(\frac{11}{8}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
3 × \(\frac{11}{8}\)
= \(\frac{3}{1}\) × \(\frac{11}{8}\)
= \(\frac{11 × 3}{1 × 8}\)
= \(\frac{33}{8}\)
Hence,
3 × \(\frac{11}{8}\) = \(\frac{33}{8}\)
Find the unknown number.
Question 12.
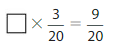
Answer:
The missing number is: 3
Explanation:
The given fractions are: \(\frac{3}{20}\) and \(\frac{9}{20}\)
Let the missing number be X
So,
X × \(\frac{3}{20}\) = \(\frac{9}{20}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{9}{20}\) ÷ \(\frac{3}{20}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{9}{20}\) ÷ \(\frac{3}{20}\)
= \(\frac{9}{20}\) × \(\frac{20}{3}\)
= \(\frac{9 × 20}{20 × 3}\)
= 3
Hence,
The missing number is: 3
Question 13.
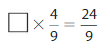
Answer:
The missing number is: 6
Explanation:
The given fractions are: \(\frac{4}{9}\) and \(\frac{24}{9}\)
Let the missing number be X
So,
X × \(\frac{4}{9}\) = \(\frac{24}{9}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{24}{9}\) ÷ \(\frac{4}{9}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{24}{9}\) ÷ \(\frac{4}{9}\)
= \(\frac{24}{9}\) × \(\frac{9}{4}\)
= \(\frac{9 × 24}{9 × 4}\)
= 6
Hence,
The missing number is: 6
Question 14.
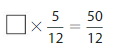
Answer:
The missing number is: 10
Explanation:
The given fractions are: \(\frac{5}{12}\) and \(\frac{50}{12}\)
Let the missing number be X
So,
X × \(\frac{5}{12}\) = \(\frac{50}{12}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{50}{12}\) ÷ \(\frac{5}{12}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{50}{12}\) ÷ \(\frac{5}{12}\)
= \(\frac{50}{12}\) × \(\frac{12}{5}\)
= \(\frac{12 × 50}{12 × 5}\)
= 10
Hence,
The missing number is: 10
Question 15.
A recipe calls for \(\frac{3}{4}\) cup of dried rice noodles. You make 44 batches of the recipe. How many cups of dried rice noodles do you use?

Answer:
The number of cups of dried rice noodles you used is: 33
Explanation:
It is given that a recipe calls for \(\frac{3}{4}\) cup of dried rice noodles.
It is also given that you make 44 batches of the recipe
So,
The number of cups of dried rice noodles you used = ( The number of batches of the recipe ) × ( The number of dried rice noodles for each batch )
= 44 × \(\frac{3}{4}\)
Now,
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
44 × \(\frac{3}{4}\)
= \(\frac{44}{1}\) × \(\frac{3}{4}\)
= \(\frac{44 × 3}{1 × 4}\)
= \(\frac{33}{1}\)
= 33
Hence, from the above,
We can conclude that the number of cups of dried noodles you used is: 33 cups
Question 16.
YOU BE THE TEACHER
Your 5 × \(\frac{3}{5}\) friend says that 5 is equal to \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\). Is your friend correct? Explain.
Answer:
Yes, your friend is correct.
Explanation:
It is given that your 5 × \(\frac{3}{5}\) friend says that 5 is equal to \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\).
Now,
We know that,
n × a = a + a + a + a + …………….. + n times
Where,
‘n’ is the multiple of a
Here,
‘a’ will be the whole number or the fraction
So,
According to the above property,
5 × \(\frac{3}{5}\) = \(\frac{3}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\) +\(\frac{3}{5}\) + \(\frac{3}{5}\)
Hence, from the above,
We can conclude that your friend is correct.
Question 17.
Patterns
Describe and complete the pattern.
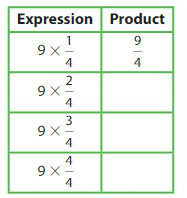
Answer:
The completed pattern is:
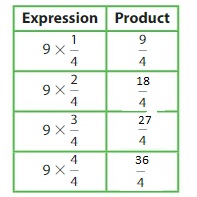
From the above pattern,
We can observe that
The whole number is constant i.e., 9
The fraction part is changing i.e., the numerator part is increasing by 1 till 4 and the denominator is constant
So,
Now,
9 × \(\frac{1}{4}\)
= \(\frac{9}{1}\) × \(\frac{1}{4}\)
= \(\frac{9 × 1}{1 × 4}\)
= \(\frac{9}{4}\)
9 × \(\frac{2}{4}\)
= \(\frac{9}{1}\) × \(\frac{2}{4}\)
= \(\frac{9 × 2}{1 × 4}\)
= \(\frac{18}{4}\)
So,
The remaining two multiplication equations will also be solved in the same way.
Think and Grow: Modeling Real Life
Example
Your goal is to make a waterslide that is at least 10 meters long. You make the waterslide using 10 plastic mats that are each \(\frac{3}{2}\) meters long. Do you reach your goal?

Find the length of the waterslide by multiplying the number of mats by the length of each mat.
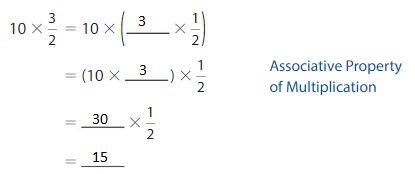
So,
You reached your goal.
Show and Grow
Question 18.
An excavator is moving 4 piles of dirt that are the same size. Each pile requires \(\frac{3}{4}\) hour to move. Can the excavator move all of the piles in 2 hours?
Answer:
No, the excavator can’t move all of the piles in 2 hours
Explanation:
It is given that an excavator is moving 4 piles of dirt that are of the same size and each pile requires \(\frac{3}{4}\) hour to move.
So,
We know that,
1 hour = 60 minutes
So,
\(\frac{3}{4}\) of 1 hour = \(\frac{3}{4}\) × 60
= \(\frac{3}{4}\) × \(\frac{60}{1}\)
= \(\frac{3 × 60}{4 × 1}\)
= 45 minutes
So,
The time is taken to move 4 piles of dirt = ( The time is taken to move each pile ) × ( The total number of piles )
= 45 × 4
=180 minutes
It is given that you have to move the piles of dirt in 2 hours but the time taken is 4 hours.
Hence, from the above,
We can conclude that the excavator can’t move all the piles in 2 hours.
Question 19.
You walk dogs \(\frac{5}{4}\) miles two times each day. How far do you walk the dogs in 1 week?

Answer:
The number of miles you walk the dogs in 1 week is: \(\frac{35}{2}\)
Explanation:
It is given that you walk dogs \(\frac{5}{4}\) miles two times each day
So,
The total number of miles you walk dogs in 1 day = 2 × \(\frac{5}{4}\)
= \(\frac{5}{4}\) × \(\frac{2}{1}\)
= \(\frac{5 × 2}{4 × 1}\)
= \(\frac{5}{2}\) miles
We know that,
1 week = 7 days
So,
The total number of miles you walk dogs in 1 week = ( The number of miles you walk dogs in 1 day ) × 7
= \(\frac{5}{2}\) × 7
= \(\frac{5}{2}\) × \(\frac{7}{1}\)
= \(\frac{5 × 7}{2 × 1}\)
= \(\frac{35}{2}\)
Hence, from the above,
We can conclude that the numebr of miles you walk dogs in 1 week is: \(\frac{35}{2}\) miles
Question 20.
DIG DEEPER
You have10 feet of string. You need \(\frac{5}{3}\) feet of string to make 1 necklace. You make 5 necklaces. Do you have enough string to make another necklace? Explain.
Answer:
Yes, we have enough string to make another necklace
Explanation:
It is given that you have 10 feet of string and you need \(\frac{5}{3}\) feet of string to make 1 necklace. and you make 5 necklaces.
So,
The length of the string required for 5 necklaces = ( The length of string required for 1 necklace ) × ( The total number of necklaces )
= \(\frac{5}{3}\) × 5
= \(\frac{5}{3}\) × \(\frac{5}{1}\)
= \(\frac{5 × 5}{3 × 1}\)
= \(\frac{25}{3}\) feet
We can write 10 feet as \(\frac{30}{3}\) feet
So,
When we compare the total length of the string and the length of the string to make 5 necklaces,
We can observe that the length of the string to make 5 necklaces is less than the total length of the string.
Hence, from the above,
We can conclude that we have enough string to make another necklace.
Multiply Whole Numbers by Fractions Homework & Practice 9.1
Multiply
Question 1.
5 × \(\frac{2}{3}\) = ______
Answer:
5 × \(\frac{2}{3}\) = \(\frac{10}{3}\)
Explanation:
The given numbers are: 5 and \(\frac{2}{3}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
5 × \(\frac{2}{3}\)
= \(\frac{5}{1}\) × \(\frac{2}{3}\)
= \(\frac{2 × 5}{1 × 3}\)
= \(\frac{10}{3}\)
Hence,
5 × \(\frac{2}{3}\) = \(\frac{10}{3}\)
Question 2.
9 × \(\frac{7}{8}\) = ______
Answer:
9 × \(\frac{7}{8}\) = \(\frac{63}{8}\)
Explanation:
The given numbers are: 9 and \(\frac{7}{8}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
9 × \(\frac{7}{8}\)
= \(\frac{9}{1}\) × \(\frac{7}{8}\)
= \(\frac{9 × 7}{1 × 8}\)
= \(\frac{63}{8}\)
Hence,
9 × \(\frac{7}{8}\) = \(\frac{63}{8}\)
Question 3.
4 × \(\frac{11}{12}\) = ______
Answer:
4 × \(\frac{11}{12}\) = \(\frac{44}{12}\)
Explanation:
The given numbers are: 4 and \(\frac{11}{12}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
4 × \(\frac{11}{12}\)
= \(\frac{4}{1}\) × \(\frac{11}{12}\)
= \(\frac{4 × 11}{1 × 12}\)
= \(\frac{44}{12}\)
Hence,
4 × \(\frac{11}{12}\) = \(\frac{44}{12}\)
Question 4.
8 × \(\frac{35}{100}\) = ______
Answer:
8 × \(\frac{35}{100}\) = \(\frac{280}{100}\)
Explanation:
The given numbers are: 8 and \(\frac{35}{100}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
8 × \(\frac{35}{100}\)
= \(\frac{8}{1}\) × \(\frac{35}{100}\)
= \(\frac{8 × 35}{1 × 100}\)
= \(\frac{280}{100}\)
Hence,
8 × \(\frac{35}{100}\) = \(\frac{280}{100}\)
Question 5.
3 × \(\frac{1}{2}\) = ______
Answer:
3 × \(\frac{1}{2}\) = \(\frac{3}{2}\)
Explanation:
The given numbers are: 3 and \(\frac{1}{2}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
3 × \(\frac{1}{2}\)
= \(\frac{3}{1}\) × \(\frac{1}{2}\)
= \(\frac{1 × 3}{1 × 2}\)
= \(\frac{3}{2}\)
Hence,
3 × \(\frac{1}{2}\) = \(\frac{3}{2}\)
Question 6.
7 × \(\frac{2}{5}\) = ______
Answer:
7 × \(\frac{2}{5}\) = \(\frac{14}{5}\)
Explanation:
The given numbers are: 7 and \(\frac{2}{5}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
7 × \(\frac{2}{5}\)
= \(\frac{7}{1}\) × \(\frac{2}{5}\)
= \(\frac{2 × 7}{1 × 5}\)
= \(\frac{14}{5}\)
Hence,
7 × \(\frac{2}{5}\) = \(\frac{14}{5}\)
Question 7.
6 × \(\frac{7}{4}\) = ______
Answer:
6 × \(\frac{7}{4}\) = \(\frac{42}{4}\)
Explanation:
The given numbers are: 6 and \(\frac{7}{4}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
6 × \(\frac{7}{4}\)
= \(\frac{6}{1}\) × \(\frac{7}{4}\)
= \(\frac{6 × 7}{1 × 4}\)
= \(\frac{42}{4}\)
Hence,
6 × \(\frac{7}{4}\) = \(\frac{42}{4}\)
Question 8.
12 × \(\frac{8}{7}\) = ______
Answer:
12 × \(\frac{8}{7}\) = \(\frac{96}{7}\)
Explanation:
The given numbers are: 12 and \(\frac{8}{7}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
12 × \(\frac{8}{7}\)
= \(\frac{12}{1}\) × \(\frac{8}{7}\)
= \(\frac{12 × 8}{1 × 7}\)
= \(\frac{96}{7}\)
Hence,
12 × \(\frac{8}{7}\) = \(\frac{96}{7}\)
Question 9.
25 × \(\frac{10}{9}\) = ______
Answer:
25 × \(\frac{10}{9}\) = \(\frac{250}{9}\)
Explanation:
The given numbers are: 25 and \(\frac{10}{9}\)
We know that,
a = \(\frac{a}{1}\)
a × \(\frac{a}{b}\) = \(\frac{a × a}{b × 1}\)
So,
25 × \(\frac{10}{9}\)
= \(\frac{25}{1}\) × \(\frac{10}{9}\)
= \(\frac{25 × 10}{1 × 9}\)
= \(\frac{250}{9}\)
Hence,
25 × \(\frac{10}{9}\) = \(\frac{250}{9}\)
Find the unknown number.
Question 10.
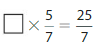
Answer:
The missing number is: 5
Explanation:
The given fractions are: \(\frac{5}{7}\) and \(\frac{25}{7}\)
Let the missing number be X
So,
X × \(\frac{5}{7}\) = \(\frac{25}{7}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{25}{7}\) ÷ \(\frac{5}{7}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{25}{7}\) ÷ \(\frac{5}{7}\)
= \(\frac{25}{7}\) × \(\frac{7}{5}\)
= \(\frac{7 × 25}{7 × 5}\)
= 5
Hence,
The missing number is: 5
Question 11.
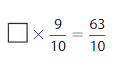
Answer:
The missing number is: 7
Explanation:
The given fractions are: \(\frac{9}{10}\) and \(\frac{63}{10}\)
Let the missing number be X
So,
X × \(\frac{9}{10}\) = \(\frac{63}{10}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{63}{10}\) ÷ \(\frac{9}{10}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{63}{10}\) ÷ \(\frac{9}{10}\)
= \(\frac{63}{10}\) × \(\frac{10}{9}\)
= \(\frac{63 × 10}{10 × 9}\)
= 7
Hence,
The missing number is: 7
Question 12.
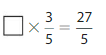
Answer:
The missing number is: 9
Explanation:
The given fractions are: \(\frac{3}{5}\) and \(\frac{27}{5}\)
Let the missing number be X
So,
X × \(\frac{3}{5}\) = \(\frac{27}{5}\)
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = \(\frac{27}{5}\) ÷ \(\frac{3}{5}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{27}{5}\) ÷ \(\frac{3}{5}\)
= \(\frac{27}{5}\) × \(\frac{5}{3}\)
= \(\frac{5 × 27}{5 × 3}\)
= 9
Hence,
The missing number is: 9
Question 13.
You make 5 servings of pancakes. You top each serving with \(\frac{1}{4}\) cup of strawberries. How many cups of strawberries do you use?
Answer:
The number of cups of strawberries you used is: 20 cups
Explanation:
It is given that you make 5 servings of pancakes and you top each serving with \(\frac{1}{4}\) cup of strawberries.
So,
The number of cups of strawberries = \(\frac{The number of servings of pancakes}{Each serving in pancake}\)
= 5 ÷ \(\frac{1}{4}\)
= \(\frac{5}{1}\) ÷ \(\frac{1}{4}\)
= \(\frac{5}{1}\) × \(\frac{4}{1}\)
= \(\frac{5 × 4}{1 × 1}\)
= 20 cups
hence, from the above,
We can conclude that the number of cups of strawberries is: 20 cups
Question 14.
Which One Doesn’tBelong?
Which one does not belong with the other three?
4 × \(\frac{3}{8}\)
3 × \(\frac{1}{8}\)
\(\frac{3}{8}\) + \(\frac{3}{8}\) + \(\frac{3}{8}\) + \(\frac{3}{8}\)
1 + \(\frac{1}{2}\)
Answer:
Let the expresseons be named A., B., C., D.
So,
A) 4 × \(\frac{3}{8}\)
B) 3 × \(\frac{1}{8}\)
C) \(\frac{3}{8}\) + \(\frac{3}{8}\) + \(\frac{3}{8}\) + \(\frac{3}{8}\)
D) 1 + \(\frac{1}{2}\)
So, from the above four expressions,
Expressions A), B), C) are in the normal form and C) is the expanded form of expression A)
Hence, from the above,
We can conclude that expression D) does not belong to the other three.
Question 15.
Modeling Real Life
You complete \(\frac{5}{2}\) inches of weaving each day for 5 days. The weaving needs to be at least 11 inches long. Is your weaving complete?

Answer:
Yes, your weaving is complete
Explanation:
It is given that you complete \(\frac{5}{2}\) inches of weaving each day for 5 days.
So,
The total number of inches you completed in 5 days = ( The number of inches you weaved each day ) × 5
= \(\frac{5}{2}\) × 5
= \(\frac{5}{2}\) × \(\frac{5}{1}\)
= \(\frac{5 × 5}{2 × 1}\)
= \(\frac{25}{2}\)
It is also given that the weaving needs to be atleast 11 inches long.
So,
11 inches can also be written as \(\frac{22}{2}\)
So,
When we compare the total number of inches needed for weaving and the total number of inches you weaved in 5 days, we can observe that
You weaved more than the amount of the weaving.
Hence, from the above,
We can conclude that your weaving is completed.
Question 16.
DIG DEEPER!
You spend \(\frac{7}{2}\) hours playing drums each day for 2 days. Your friend spends \(\frac{5}{4}\) hours playing drums each day for 6 days. Who spends more time playing drums? How much more?

Answer:
Your friend spend more time playing drums than you
The amount you played drums more than your friend is: \(\frac{1}{2}\) hours
Explanation:
It is given that you spend \(\frac{7}{2}\) hours each day playing drums for 2 days
So,
The time you played drums for 2 days = The time you played drums for each day × 2
= \(\frac{7}{2}\) × 2
= \(\frac{7}{2}\) × \(\frac{2}{1}\)
= \(\frac{7 × 2}{2 × 1}\)
= \(\frac{14}{2}\)
= \(\frac{28}{4}\)
= 7 hours
It is also given that Your friend spends \(\frac{5}{4}\) hours playing drums each day for 6 days.
So,
The time your friend played drums for 6 days = The time your friend played drums for each day × 6
= \(\frac{5}{4}\) × 6
= \(\frac{5}{4}\) × \(\frac{6}{1}\)
= \(\frac{5 × 6}{4 × 1}\)
= \(\frac{30}{4}\) hours
Now,
When we compare the time played drums by you and your friends, your friend played more time than you
So,
The amount of time more your friend played than you = \(\frac{30}{4}\) – \(\frac{28}{4}\)
= \(\frac{30 – 28}{4}\)
= \(\frac{2}{4}\)
= \(\frac{1}{2}\) hour
Hence, from the above,
We can conclude that
Your friend spend more time playing drums than you
The amount you played drums more than your friend is: \(\frac{1}{2}\) hours
Review & Refresh
Find the product.
Question 17.
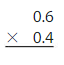
Answer:
0.6 × 0.4 = 0.24
Explanation:
The given decimal numbers are: 0.6 and 0.4
the representation of the decimal numbers in the fraction form is: \(\frac{6}{10}\) and \(\frac{4}{10}\)
Now,
\(\frac{6}{10}\) × \(\frac{4}{10}\)
= \(\frac{6 × 4}{10 × 10}\)
= \(\frac{24}{100}\)
So,
The representation of \(\frac{24}{100}\) in the decimal form is: 0.24
Hence, 0.6 × 0.4 = 0.24
Question 18.
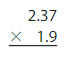
Answer:
2.37 × 1.9 = 4.503
Explanation:
The given decimal numbers are: 2.37 and 1.9
the representation of the decimal numbers in the fraction form is: \(\frac{237}{100}\) and \(\frac{19}{10}\)
Now,
\(\frac{237}{100}\) × \(\frac{19}{10}\)
= \(\frac{237 × 19}{100 × 10}\)
= \(\frac{4,503}{1000}\)
So,
The representation of \(\frac{4503}{1000}\) in the decimal form is: 4.503
Hence, 2.37 × 1.9 = 4.503
Question 19.
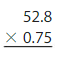
Answer:
52.8 × 0.75 = 39.6
Explanation:
The given decimal numbers are: 52.8 and 0.75
the representation of the decimal numbers in the fraction form is: \(\frac{6}{10}\) and \(\frac{4}{10}\)
Now,
\(\frac{528}{10}\) × \(\frac{75}{100}\)
= \(\frac{528 × 75}{10 × 100}\)
= \(\frac{3960}{1000}\)
So,
The representation of \(\frac{3960}{1000}\) in the decimal form is: 39.6
Hence, 52.8 × 0.75 = 39.6
Lesson 9.2 Use Models to Multiply Fractions by Whole Numbers
You need to give water to \(\frac{2}{3}\) of the dogs at a shelter. There are 12 dogs at the shelter. How many dogs need water? Draw a model to support your answer.
Answer:
The number of dogs that need water is: 8 dogs
Explanation:
It is given that you need to give water to \(\frac{2}{3}\) of the dogs at a shelter and there are 12 dogs at the shelter
So,
The number of dogs that need water = ( The fraction of dogs that need water ) × ( The total number of dogs )
= \(\frac{2}{3}\) × 12
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{3}\) × 12
= \(\frac{2}{3}\) × \(\frac{12}{1}\)
= \(\frac{2 × 12}{3 × 1}\)
= \(\frac{8}{1}\)
= 8
Hence, from the above,
We can conclude that there are 8 dogs that need water
Reasoning
How can you use a model to multiply a fraction by a whole number? Explain.
Answer:
We can multiply a fraction by a whole number by using the following multiplication properties. They are:
A) \(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
B) x = \(\frac{x}{1}\)
Think and Grow: Multiply Fractions by Whole Numbers
You can use models to multiply a fraction by a whole number.
Example
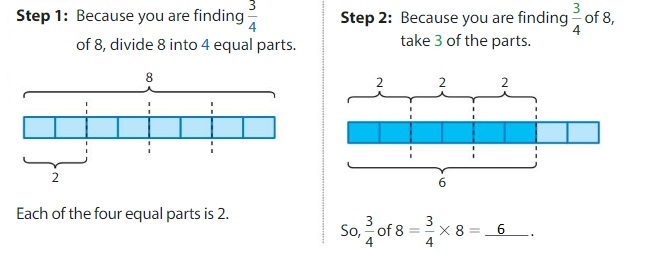
Find \(\frac{3}{4}\) of 8.
Example
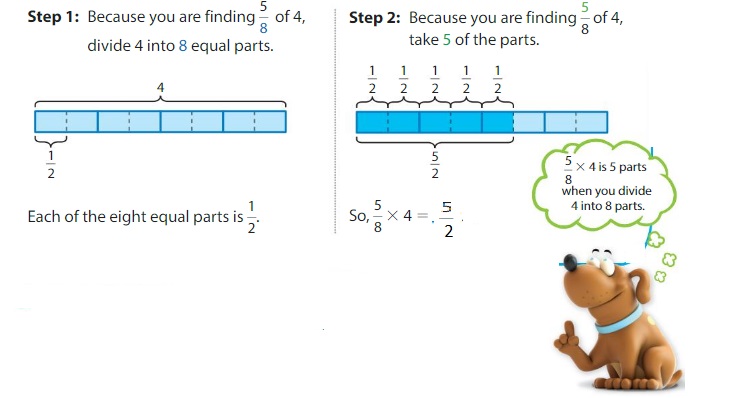
Find \(\frac{5}{8}\) × 4.
Show and Grow
Question 1.
Find \(\frac{2}{5}\) of 10.
Answer:
\(\frac{2}{5}\) × 10 = 4
Explanation:
The given numbers are: \(\frac{2}{5}\) and 10
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{5}\) × 10 = \(\frac{2}{5}\) × \(\frac{10}{1}\)
= \(\frac{2 × 10}{5 × 1}\)
= \(\frac{4}{1}\)
= 4
Hence,
\(\frac{2}{5}\) × 10 = 4
Question 2.
Find \(\frac{7}{12}\) × 6.
Answer:
\(\frac{7}{12}\) × 6 = \(\frac{7}{2}\)
Explanation:
The given numbers are: \(\frac{7}{12}\) and 6
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{7}{12}\) × 6 = \(\frac{7}{12}\) × \(\frac{6}{1}\)
= \(\frac{7 × 6}{12 × 1}\)
= \(\frac{7}{2}\)
Hence,
\(\frac{7}{12}\) × 6 = \(\frac{7}{2}\)
Apply and Grow: Practice
Multiply. Use a model to help.
Question 3.
\(\frac{5}{6}\) of 12
Answer:
\(\frac{5}{6}\) × 12 = 10
Explanation:
The given numbers are: \(\frac{5}{6}\) and 12
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{5}{6}\) × 12 = \(\frac{5}{6}\) × \(\frac{12}{1}\)
= \(\frac{5 × 12}{6 × 1}\)
= \(\frac{10}{1}\)
= 10
Hence,
\(\frac{5}{6}\) × 12 = 10
Question 4.
\(\frac{2}{3}\) × 9
Answer:
\(\frac{2}{3}\) × 9 = 6
Explanation:
The given numbers are: \(\frac{2}{3}\) and 9
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{3}\) × 9 = \(\frac{2}{3}\) × \(\frac{9}{1}\)
= \(\frac{2 × 9}{3 × 1}\)
= \(\frac{6}{1}\)
= 6
Hence,
\(\frac{2}{3}\) × 9 = 6
Question 5.
\(\frac{1}{5}\) × 10
Answer:
\(\frac{1}{5}\) × 10 = 2
Explanation:
The given numbers are: \(\frac{1}{5}\) and 10
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{5}\) × 10 = \(\frac{1}{5}\) × \(\frac{10}{1}\)
= \(\frac{1 × 10}{5 × 1}\)
= \(\frac{2}{1}\)
= 2
Hence,
\(\frac{1}{5}\) × 10 = 2
Question 6.
\(\frac{3}{5}\) of 5
Answer:
\(\frac{3}{5}\) × 5 = 3
Explanation:
The given numbers are: \(\frac{3}{5}\) and 5
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{3}{5}\) × 5 = \(\frac{3}{5}\) × \(\frac{5}{1}\)
= \(\frac{3 × 5}{5 × 1}\)
= \(\frac{3}{1}\)
= 3
Hence,
\(\frac{3}{5}\) × 5 = 3
Question 7.
\(\frac{1}{6}\) of 3
Answer:
\(\frac{1}{6}\) × 3 = \(\frac{1}{2}\)
Explanation:
The given numbers are: \(\frac{1}{6}\) and 3
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{6}\) × 3 = \(\frac{1}{6}\) × \(\frac{3}{1}\)
= \(\frac{1 × 3}{6 × 1}\)
= \(\frac{1}{2}\)
Hence,
\(\frac{1}{6}\) × 3 = \(\frac{1}{2}\)
Question 8.
\(\frac{3}{8}\) × 4
Answer:
\(\frac{3}{8}\) × 4 = \(\frac{3}{2}\)
Explanation:
The given numbers are: \(\frac{3}{8}\) and 4
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{3}{8}\) × 4 = \(\frac{3}{8}\) × \(\frac{4}{1}\)
= \(\frac{3 × 4}{8 × 1}\)
= \(\frac{3}{2}\)
Hence,
\(\frac{3}{8}\) × 4 = \(\frac{3}{2}\)
Question 9.
You have 25 beads. You use \(\frac{2}{5}\) of the beads to make a bracelet. How many beads do you use?
Answer:
The number of beads you used is: 10 beads
Explanation:
It is given that you have 25 beads and you use \(\frac{2}{5}\) of the beads to make a bracelet.
So,
The number of beads you used = ( The fraction of beads used to make 1 bracelet ) × ( The total number of beads )
= \(\frac{2}{5}\) × 25
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{5}\) × 25 = \(\frac{2}{5}\) × \(\frac{25}{1}\)
= \(\frac{2 × 25}{5 × 1}\)
= \(\frac{10}{1}\)
= 10 beads
Hence, from the above,
We can conclude that the number of beads you used to make bracelets are: 10 beads
Question 10.
Writing
Write and solve a real-life problem for the expression.
\(\frac{3}{4}\) × 20
Answer:
Suppose there are 20 passengers in a bus and they occupied the place \(\frac{3}{4}\) of the bus.
Hence,
The total number of seats in the bus = ( The fraction of the place occupied by the passengers ) × ( The total number of passengers )
= \(\frac{3}{4}\) × 20
Now,
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{3}{4}\) × 20 = \(\frac{3}{4}\) × \(\frac{20}{1}\)
= \(\frac{3 × 20}{4 × 1}\)
= \(\frac{15}{1}\)
= 15 seats
Hence, from the above,
We can conclude that there are 15 seats in the bus.
Question 11.
YOU BE THE TEACHER
Descartes finds \(\frac{2}{3}\) × 6. Is he correct? Explain.
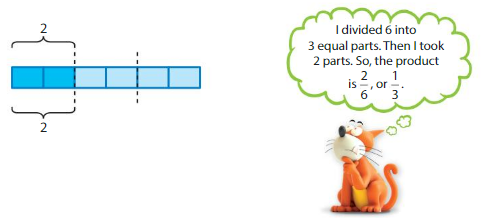
Answer:
No, Descartes is not correct
Explanation:
According to Descartes,
The given numbers are: \(\frac{2}{3}\) and 6
So,
According to Descartes, 6 is divided into 3 equal parts
So,
6 ÷ 3 = 2 equal parts
So,
According to Descartes, these 2 equal parts also divided into 2 parts.
So,
The total number of parts = 2 equal parts + 2 equal parts = 4 parts
So,
The product of \(\frac{2}{3}\) and 6 is 4
Now,
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{3}\) × 6 = \(\frac{2}{3}\) × \(\frac{6}{1}\)
= \(\frac{6 × 2}{3 × 1}\)
= \(\frac{4}{1}\)
= 4
Hence, from the above,
We can conclude that Descartes is not correct.
Think and Grow: Modeling Real Life
Example
A recipe calls for 2 cups of rice. You only have \(\frac{3}{4}\) of that amount. How much more rice do you need?

Find the number of cups of rice that you have by finding \(\frac{3}{4}\) of 2.
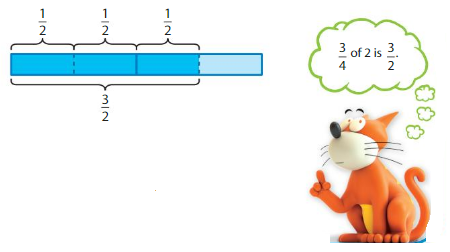
So,
You have \(\frac{3}{2}\) cups of rice.
Subtract the amount of rice you have from the amount of rice you need.
2 – \(\frac{3}{2}\) = \(\frac{2}{1}\) – \(\frac{3}{2}\)
= \(\frac{(2 × 2) – 3}{2}\)
= \(\frac{1}{2}\)
So,
you need \(\frac{1}{2}\) cup more of rice.
Show and Grow
Question 12.
You have 12 tokens. You use \(\frac{3}{4}\) of them to play a pinball game. How many tokens do you have left?
Answer:
The number of tokens you have left is: 3 tokens
Explanation:
It is given that you have 12 tokens and you use \(\frac{3}{4}\) of them to play a pinball game.
So,
The number of tokens used to play a pinball game = ( The fraction of tokens used to play a pinball game ) × ( The total number of tokens )
= \(\frac{3}{4}\) × 12
= \(\frac{3}{4}\) × \(\frac{12}{1}\)
= \(\frac{3 × 12}{4 × 1}\)
= \(\frac{9}{1}\)
= 9 tokens
So,
The number of tokens left = ( The total number of tokens ) – ( The number of tokens used to play the pinball )
= 12 – 9
= 3 tokens
Hence, from the above,
We can conclude that the number of tokens left are: 3 tokens
Question 13.
A male lion sleeps \(\frac{5}{6}\) × 6 hours of each day. How many hours does the lion sleep in 1 week?

Answer:
The number of hours the lion sleeps in 1 week is: 35 hours
Explanation:
It is given that a male lion sleeps \(\frac{5}{6}\) × 6 hours of each day
So,
The number of hours the lion sleeps in 1 day = \(\frac{5}{6}\) × 6 hours
= \(\frac{5}{6}\) × \(\frac{6}{1}\)
= \(\frac{5 × 6}{6 × 1}\)
= \(\frac{5}{1}\)
= 5 hours
We know that,
1 week = 7 days
So,
The total number of hours the lion sleeps in 1 week = ( The number of hours the lion sleeps in 1 day ) × ( The number od fays in 1 week )
= 5 × 7
= 35 hours
Hence, from the above,
We can conclude that the lion sleeps for 35 hours in 1 week
Question 14.
DIG DEEPER!
In a class of 20 students, \(\frac{1}{10}\) of the students are 10 years old, \(\frac{4}{5}\)of the students are 11 years old, and the rest are 12 years old. How many more 11-year-olds than 12-year-olds are in the class?
Answer:
The number of 11-year-olds more than 12-year-olds is: 14
Explanation:
It is given that in a class of 20 students, \(\frac{1}{10}\) of the students are 10 years old, \(\frac{4}{5}\)of the students are 11 years old, and the rest are 12 years old.
So,
The number of 10-year-olds = ( The fraction of 10-year-olds ) × ( The total number of students )
= \(\frac{1}{10}\) × 20
= \(\frac{1 × 20}{10 × 1}\)
= 2 10-year-olds
The number of 11-year-olds = ( The fraction of 11-year-olds ) × ( The total number of students )
= \(\frac{4}{5}\) × 20
= \(\frac{4}{5}\) × \(\frac{20}{1}\)
= \(\frac{4 × 20}{5 × 1}\)
= \(\frac{16}{1}\)
= 16 11-year-olds
So,
The number of 12-year-olds = ( The total number of students ) – ( The number of 10-year-olds + The number of 11-year-olds )
= 20 – ( 16 + 2 )
= 2 12-year-olds
So,
The number of 11-year-olds more than 12-year-olds = ( The number of 11-year-olds ) – ( The numebr of 12-year-olds )
= 16 – 2
= 14 students
Hence, from the above,
We can conclude that there are 14 students who are 11-years-old more than 12-years-old.
Use Models to Multiply Fractions by Whole Numbers Homework & Practice 9.2
Multiply. Use a model to help.
Question 1.
\(\frac{2}{3}\) × 6
Answer:
\(\frac{2}{3}\) × 6 = 4
Explanation:
The given numbers are: \(\frac{2}{3}\) and 6
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{3}\) × 6 = \(\frac{2}{3}\) × \(\frac{6}{1}\)
= \(\frac{2 × 6}{3 × 1}\)
= \(\frac{4}{1}\)
= 4
Hence,
\(\frac{2}{3}\) × 6 = 4
Question 2.
\(\frac{3}{5}\) of 10
Answer:
\(\frac{3}{5}\) × 10 = 6
Explanation:
The given numbers are: \(\frac{3}{5}\) and 10
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{3}{5}\) × 10 = \(\frac{3}{5}\) × \(\frac{10}{1}\)
= \(\frac{3 × 10}{5 × 1}\)
= \(\frac{6}{1}\)
= 6
Hence,
\(\frac{3}{5}\) × 10 = 6
Question 3.
\(\frac{1}{2}\) of 4
Answer:
\(\frac{1}{2}\) × 4 = 2
Explanation:
The given numbers are: \(\frac{1}{2}\) and 4
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{2}\) × 4 = \(\frac{1}{2}\) × \(\frac{4}{1}\)
= \(\frac{1 × 4}{2 × 1}\)
= \(\frac{2}{1}\)
= 2
Hence,
\(\frac{1}{2}\) × 4 = 2
Question 4.
\(\frac{1}{4}\) × 12
Answer:
\(\frac{1}{4}\) × 12 = 3
Explanation:
The given numbers are: \(\frac{1}{4}\) and 12
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{4}\) × 12 = \(\frac{1}{4}\) × \(\frac{12}{1}\)
= \(\frac{1 × 12}{4 × 1}\)
= \(\frac{3}{1}\)
= 3
Hence,
\(\frac{1}{12}\) × 4 = 3
Question 5.
\(\frac{5}{6}\) × 3
Answer:
\(\frac{5}{6}\) × 3 = \(\frac{5}{2}\)
Explanation:
The given numbers are: \(\frac{5}{6}\) and 3
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{5}{6}\) × 3 = \(\frac{5}{6}\) × \(\frac{3}{1}\)
= \(\frac{5 × 3}{6 × 1}\)
= \(\frac{5}{2}\)
Hence,
\(\frac{5}{6}\) × 3 = \(\frac{5}{2}\)
Question 6.
\(\frac{3}{4}\) of 2
Answer:
\(\frac{3}{4}\) × 2 = \(\frac{3}{2}\)
Explanation:
The given numbers are: \(\frac{3}{4}\) and 2
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{3}{4}\) × 2 = \(\frac{3}{4}\) × \(\frac{2}{1}\)
= \(\frac{3 × 2}{4 × 1}\)
= \(\frac{3}{2}\)
Hence,
\(\frac{3}{4}\) × 2 = \(\frac{3}{2}\)
Question 7.
You have 27 foam balls. You use \(\frac{1}{3}\) of the balls for a model. How many balls do you use?

Answer:
The number of balls you used is: 9 balls
Explanation:
It is given that there are 27 foam balls and you use \(\frac{1}{3}\) of the balls for a model.
So,
The number of balls you used = ( The fraction of balls you used ) × ( The total number of balls )
= \(\frac{1}{3}\) × 27
Now,
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{3}\) × 27 = \(\frac{1}{3}\) × \(\frac{27}{1}\)
= \(\frac{1 × 27}{3 × 1}\)
= \(\frac{9}{1}\)
= 9 balls
Hence, from the above,
We can conclude that the number of foam balls you used are: 27
Question 8.
An object that weighs 1 pound on Earth weighs about \(\frac{1}{15}\) pound on Pluto. A man weighs 240 pounds on Earth. How many pounds does he weigh on Pluto?
Answer:
The number of pounds the man weigh in Pluto is: 16 pounds
Explanation:
It is given that an object that weighs 1 pound on Earth weighs about \(\frac{1}{15}\) pound on Pluto.
It is also given that a man weighs 240 pounds on Earth.
So,
The weight of a man on pluto = ( The fraction of weight of a man on pluto when compared to earth ) × ( The weight of the man on earth )
= \(\frac{1}{15}\) × 240
Now,
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{1}{15}\) × 240 = \(\frac{1}{15}\) × \(\frac{240}{1}\)
= \(\frac{1 × 240}{15 × 1}\)
= \(\frac{16}{1}\)
= 16 pounds
Hence, from the above,
We can conclude that the weight of the man on pluto is: 16 pounds
Question 9.
Structure
Write a multiplication equation represented by the model.
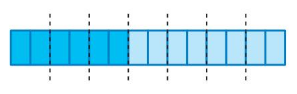
Answer:
Question 10.
DIG DEEPER!
Find each missing number.
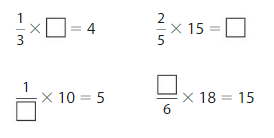
Answer:
Let the expression be named A), B), C), and D)
So,
The missing number of A is: 12
The missing number of B is: 6
The missing number of C is: 2
The missing number of D is: 5
Explanation:
Let the expressions be named as A), B), C), and D)
So,
A) The given fractions are: \(\frac{1}{3}\) and 4
Let the missing number be X
So,
X × \(\frac{1}{3}\) = 4
When multiplication goes from left to right or from right to left, it will become the division
When division goes from left to right or from right to left, it will become multiplication.
So,
X = 4 ÷ \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) ÷ \(\frac{x}{y}\) = \(\frac{a}{b}\) × \(\frac{y}{x}\)
So,
\(\frac{4}{1}\) ÷ \(\frac{1}{3}\)
= \(\frac{4}{1}\) × \(\frac{3}{1}\)
= \(\frac{4 × 3}{1 × 1}\)
= 12
Hence, the missing number is 12
B) The given numbers are: \(\frac{2}{5}\) and 15
We know that,
\(\frac{a}{b}\) × x = \(\frac{a}{b}\) × \(\frac{x}{1}\)
= \(\frac{a × x}{b × 1}\)
So,
\(\frac{2}{5}\) × 15 = \(\frac{2}{5}\) × \(\frac{15}{1}\)
= \(\frac{2 × 15}{5 × 1}\)
= \(\frac{6}{1}\)
= 6
Hence,
\(\frac{2}{5}\) × 15 = 6
Like the above two expressions, the remaining two expressions can also be solved.
hence, from the above,
We can conclude that
The missing number of A is: 12
The missing number of B is: 6
The missing number of C is: 2
The missing number of D is: 5
Question 11.
Modeling Real Life
You have 28 craft sticks. You use \(\frac{4}{7}\) of them for a project. How many craft sticks do you have left?
Answer:
The number of craft sticks you have left is: 12 craft sticks
Explanation:
It is given that you have 28 craft sticks and you used \(\frac{4}{7}\) of them for a project.
So,
The number of craft sticks you used = ( The fraction of craft sticks you used ) × ( The total number of craft sticks )
= \(\frac{4}{7}\) × 28
= \(\frac{4}{7}\) × \(\frac{28}{1}\)
= \(\frac{4 × 28}{7 × 1}\)
= \(\frac{16}{1}\)
= 16
So,
The number of craft sticks you left = ( The total number of craft sticks ) – ( The number of craft sticks you used )
= 28 – 16
= 12 craft sticks
Hence, from the above,
We can conclude that the number of craft sticks you left is: 12 craft sticks
Question 12.
Modeling Real Life
A mother otter spends \(\frac{1}{3}\) of each day feeding her baby. How many hours does the mother otter spend feeding her baby in 1 week?

Answer:
The number of hours the mother otter spend feeding her baby in 1 week is: 56 hours
Explanation:
It is given that a mother otter spends \(\frac{1}{3}\) of each day feeding her baby.
We know that,
1 day = 24 hours
So,
The number of hours the mother otter spends feeding her baby in 1 day = ( The fraction of time the mother otter spends in feeding milk ) × 24
= \(\frac{1}{3}\) × 24
= \(\frac{1}{3}\) × \(\frac{24}{1}\)
= \(\frac{1 × 24}{3 × 1}\)
= \(\frac{8}{1}\)
= 8 hours
Now,
We know that,
1 week = 7 days
So,
The number of hours the mother otter spends feeding her milk in 1 week = ( The number of hours the mother otter feeding her milk in 1 day ) × 7
= 8 × 7
= 56 hours
Hence, from the above,
We can conclude that the mother otter spends feeding her milk for 56 hours in 1 week
Review & Refresh
Estimate the quotient.
Question 13.
5,692 ÷ 5
Answer:
5,692 ÷ 5 =1,138 R 2
Explanation:
By using the partial quotients method,
5,692 ÷ 5 = ( 5,000 + 600 + 90 ) ÷ 5
= ( 5,000 ÷ 5 ) + ( 600 ÷ 5 ) + ( 90 ÷ 5 )
= 1,000 + 120 + 18
= 1,138 R 2
Hence, 5,692 ÷ 5 = 1,138 R 2
Question 14.
309 ÷ 12
Answer:
309 ÷ 12 = 25 R 9
Explanation:
By using the partial quotients method,
309 ÷ 12 = ( 240 + 60 ) ÷ 12
= ( 240 ÷ 12 ) + ( 60 ÷ 12 )
= 20 + 5
= 25 R 9
Hence, 309 ÷ 12 = 25 R 2
Question 15.
2,987 ÷ 53
Answer:
2,987 ÷ 53 = 2,987 ÷ ( 50 + 3 )
= ( 2,985 ÷ 50 ) + ( 2,985 ÷ 3 )
= 995 R 2 + 59.7
= 1,054.7 R 2
Lesson 9.3 Multiply Fractions and Whole Numbers
Explore and Grow
Use models to help you complete the table. What do you notice about each expression and its product?
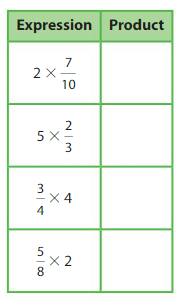
Answer:
The completed table is:
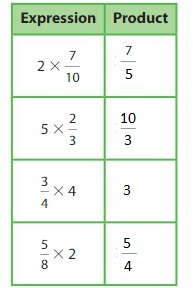
From the completed table,
We can observe the multiplication of the whole number and the fraction.
The product of a whole number and a fraction may be a whole number or a fraction.
Construct Arguments
Explain how to multiply fractions and whole numbers without using models.
Answer:
We can multiply the whole numbers and fractions by using the properties of the multiplication. They are:
A) \(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
B) p = \(\frac{p}{1}\)
Think and Grow: Multiply Fractions and Whole Numbers
Key Idea
You can find the product of a fraction and a whole number by multiplying the numerator and the whole number. Then write the result over the denominator.
Example
Find 2 × \(\frac{5}{6}\).
Multiply the numerator and the whole number.
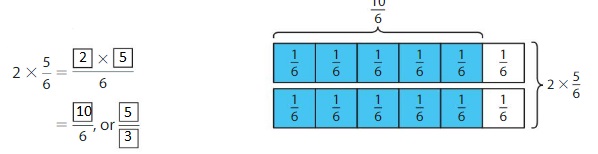
Example
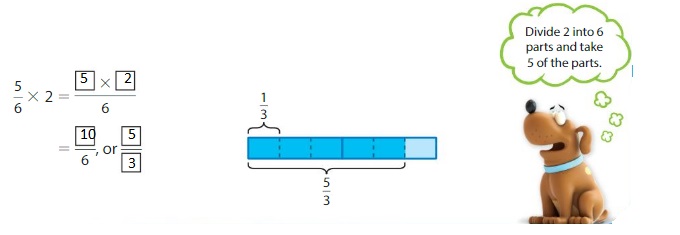
Find \(\frac{5}{6}\) × 2
Multiply the numerator and the whole number.
Show and Grow
Multiply.
Question 1.
3 × \(\frac{5}{8}\) = _______
Answer:
3 × \(\frac{5}{8}\) = \(\frac{15}{8}\)
Explanation:
The given numbers are: 3 and \(\frac{5}{8}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
3 × \(\frac{5}{8}\) = \(\frac{3}{1}\) × \(\frac{5}{8}\)
= \(\frac{5 × 3}{8 × 1}\)
= \(\frac{15}{8}\)
Hence,
3 × \(\frac{5}{8}\) = \(\frac{15}{8}\)
Question 2.
6 × \(\frac{4}{9}\) = _______
Answer:
6 × \(\frac{4}{9}\) = \(\frac{8}{3}\)
Explanation:
The given numbers are: 6 and \(\frac{4}{9}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
6 × \(\frac{4}{9}\) = \(\frac{6}{1}\) × \(\frac{4}{9}\)
= \(\frac{6 × 4}{9 × 1}\)
= \(\frac{24}{9}\)
= \(\frac{8}{3}\)
Hence,
6 × \(\frac{4}{9}\) = \(\frac{8}{3}\)
Question 3.
\(\frac{2}{5}\) × 15 = _______
Answer:
15 × \(\frac{2}{5}\) = 6
Explanation:
The given numbers are: 15 and \(\frac{2}{5}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
15× \(\frac{2}{5}\) = \(\frac{15}{1}\) × \(\frac{2}{5}\)
= \(\frac{15 × 2}{5 × 1}\)
= \(\frac{6}{1}\)
= 6
Hence,
15 × \(\frac{2}{5}\) = 6
Apply and Grow: Practice
Multiply.
Question 4.
\(\frac{3}{5}\) × 2 = _______
Answer:
2 × \(\frac{3}{5}\) = \(\frac{6}{5}\)
Explanation:
The given numbers are: 2 and \(\frac{3}{5}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
2 × \(\frac{3}{5}\) = \(\frac{2}{1}\) × \(\frac{3}{5}\)
= \(\frac{2 × 3}{5 × 1}\)
= \(\frac{6}{5}\)
Hence,
2 × \(\frac{3}{5}\) = \(\frac{6}{5}\)
Question 5.
5 × \(\frac{2}{9}\) = _______
Answer:
5 × \(\frac{2}{9}\) = \(\frac{10}{9}\)
Explanation:
The given numbers are: 5 and \(\frac{2}{9}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
5 × \(\frac{2}{9}\) = \(\frac{5}{1}\) × \(\frac{2}{9}\)
= \(\frac{5 × 2}{9 × 1}\)
= \(\frac{10}{9}\)
Hence,
5 × \(\frac{2}{9}\) = \(\frac{10}{9}\)
Question 6.
\(\frac{5}{6}\) × 4 = _______
Answer:
4 × \(\frac{5}{6}\) = \(\frac{10}{3}\)
Explanation:
The given numbers are: 4 and \(\frac{5}{6}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
4 × \(\frac{5}{6}\) = \(\frac{4}{1}\) × \(\frac{5}{6}\)
= \(\frac{5 × 4}{6 × 1}\)
= \(\frac{20}{6}\)
= \(\frac{10}{3}\)
Hence,
4 × \(\frac{5}{6}\) = \(\frac{10}{3}\)
Question 7.
8 × \(\frac{3}{10}\) = _______
Answer:
8 × \(\frac{3}{10}\) = \(\frac{12}{5}\)
Explanation:
The given numbers are: 8 and \(\frac{3}{10}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
8 × \(\frac{3}{10}\) = \(\frac{8}{1}\) × \(\frac{3}{10}\)
= \(\frac{8 × 3}{10 × 1}\)
= \(\frac{24}{10}\)
= \(\frac{12}{5}\)
Hence,
8 × \(\frac{3}{10}\) = \(\frac{12}{5}\)
Question 8.
\(\frac{1}{5}\) × 7 = _______
Answer:
7 × \(\frac{1}{5}\) = \(\frac{7}{5}\)
Explanation:
The given numbers are: 7 and \(\frac{1}{5}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
7 × \(\frac{1}{5}\) = \(\frac{7}{1}\) × \(\frac{1}{5}\)
= \(\frac{7 × 1}{5 × 1}\)
= \(\frac{7}{5}\)
Hence,
7 × \(\frac{1}{5}\) = \(\frac{7}{5}\)
Question 9.
9 × \(\frac{5}{12}\) = _______
Answer:
9 × \(\frac{5}{12}\) = \(\frac{15}{4}\)
Explanation:
The given numbers are: 9 and \(\frac{5}{12}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
9 × \(\frac{5}{12}\) = \(\frac{9}{1}\) × \(\frac{5}{12}\)
= \(\frac{9 × 5}{12 × 1}\)
= \(\frac{45}{12}\)
= \(\frac{15}{4}\)
Hence,
9 × \(\frac{5}{12}\) = \(\frac{15}{4}\)
Question 10.
15 × \(\frac{5}{8}\) = _______
Answer:
15 × \(\frac{5}{8}\) = \(\frac{75}{8}\)
Explanation:
The given numbers are: 15 and \(\frac{5}{8}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
15 × \(\frac{5}{8}\) = \(\frac{15}{1}\) × \(\frac{5}{8}\)
= \(\frac{15 × 5}{8 × 1}\)
= \(\frac{75}{8}\)
Hence,
15 × \(\frac{5}{8}\) = \(\frac{75}{8}\)
Question 11.
\(\frac{3}{4}\) × 20 = _______
Answer:
20 × \(\frac{3}{4}\) = 15
Explanation:
The given numbers are: 20 and \(\frac{3}{4}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
20 × \(\frac{3}{4}\) = \(\frac{20}{1}\) × \(\frac{3}{4}\)
= \(\frac{20 × 3}{4 × 1}\)
= \(\frac{60}{4}\)
= \(\frac{15}{1}\)
= 15
Hence,
20 × \(\frac{3}{4}\) = 15
Question 12.
\(\frac{7}{9}\) × 5 = _______
Answer:
5 × \(\frac{7}{9}\) = \(\frac{35}{9}\)
Explanation:
The given numbers are: 5 and \(\frac{7}{9}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
5 × \(\frac{7}{9}\) = \(\frac{5}{1}\) × \(\frac{7}{9}\)
= \(\frac{5 × 7}{9 × 1}\)
= \(\frac{35}{9}\)
Hence,
5 × \(\frac{7}{9}\) = \(\frac{35}{9}\)
Question 13.
One-tenth of the 50 states in the United States of America have a mockingbird as their state bird. How many states have a mockingbird as their state bird?

Answer:
The number of states that have mockingbird as their state bird is: 5 states
Explanation:
It is given that one-tenth of the 50 states in the United States of America have a mockingbird as their state bird
So,
The number of states that have a mockingbird as their state bird = ( The fraction of the states that have a mockingbird as their state bird ) × ( The total number of states in the United States of America )
= \(\frac{1}{10}\) × 50
Now,
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
50 × \(\frac{1}{10}\) = \(\frac{50}{1}\) × \(\frac{1}{10}\)
= \(\frac{50 × 1}{10 × 1}\)
= \(\frac{50}{10}\)
= \(\frac{5}{1}\)
= 5 states
Hence, from the above,
We can conclude that there are 5 states that have mockingbird as their state bird
Question 14.
Writing
Explain why 9 × \(\frac{2}{3}\) is equivalent to \(\frac{2}{3}\) × 9.
Answer:
By using the Commutative property of multiplication,
a × b = b × a
So,
By using the above property,
In 9 × \(\frac{2}{3}\),
‘a’ is: 9
‘b’ is: \(\frac{2}{3}\)
Hence, from the above,
We can conclude that 9 × “\(\frac{2}{3}\)” is equivalent to “\(\frac{2}{3}\) × 9″ by using the Commutative property of multiplication.
Question 15.
Reasoning
Without calculating, determine which product is greater. Explain.
\(\frac{1}{8}\) × 24
\(\frac{7}{8}\) × 24
Answer:
The product of “\(\frac{7}{8}\) × 24″ is greater than “\(\frac{1}{8}\) × 24″
Explanation:
The given products are: \(\frac{1}{8}\) × 24 and \(\frac{7}{8}\) × 24
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So, from the above fractions,
We can observe that except numerator, the denominator and the whole number is all the same.
So,
To find which product is greater, we just have to compare the numerators of the two fractions without calculating the value of the product.
In the comparison of the numerators,
We can observe that,
1 < 7
So,
First fraction numerator < Second fraction numerator
Hence, from the above,
We can conclude that the product of “\(\frac{7}{8}\) × 24″ is greater than “\(\frac{1}{8}\) × 24″
Think and Grow: Modeling Real Life
Example
Newton buys 27 songs. Two-thirds of them are classical songs. Descartes buys 16 songs. Seven-eighths of them are classical songs. Who buys more classical songs? How many more?

Multiply \(\frac{2}{3}\) by 27 to find the number of classical songs Newton buys. Multiply \(\frac{7}{8}\) by 16 to find the number Descartes buys.

So, Newton buys more classical songs.
Subtract the products to find how many more.
18 – 14 = 4
Hence,
Newton buys 4 more classical songs than Descartes.
Show and Grow
Question 16.
You take 48 pictures on a walking tour. Five-twelfths of them is of buildings. Your friend takes 45 pictures. Six-fifteenths of them are of buildings. Who takes more pictures of buildings? How many more?
Answer:
You take more pictures
You take 2 pictures more than your friend
Explanation:
It is given that you take 48 pictures on a walking tour and five-twelfths if them is of buildings.
So,
The number of buildings taken by you = ( The total number of pictures taken by you ) × ( The fraction of pictures that is of buildings )
= 48 × \(\frac{5}{12}\)
= \(\frac{48}{1}\) × \(\frac{5}{12}\)
= \(\frac{48 × 5}{1 × 12}\)
= 20 pictures
It is also given that your friend taken 45 pictures and six-fifteenth of them is buildings
So,
The number of buildings taken by your friend = ( The total number of pictures taken by your friend ) × ( The fraction of pictures that is of buildings )
= 45 × \(\frac{6}{15}\)
= \(\frac{45}{1}\) × \(\frac{6}{15}\)
= \(\frac{45 × 6}{1 × 15}\)
= 18 pictures
So,
In the comparison of the pictures of buildings,
You take more pictures than your friend.
Now,
The number of pictures more taken by you than your friend = ( The number of pictures taken by you ) – ( The number of pictures taken by your friend )
= 20 – 18
= 2 pictures
Hence, from the above,
We can conclude that
You take more pictures
You take 2 pictures more than your friend
Question 17.
You have 72 rocks in your rock collection. Five-eighths of them are sedimentary, one-sixth of them are igneous, and the rest are metamorphic. How many of your rocks are metamorphic?
Answer:
The number of rocks that are metamorphic is: 15 metamorphous rocks
Explanation:
It is given that you have 72 rocks in your rock collection and five-eighths of them are sedimentary, one-sixth of them are igneous, and the rest are metamorphic.
So,
The number of rocks that are sedimentary = ( The total number of rocks ) × ( The fraction of rocks that are sedimentary )
= 72 × \(\frac{5}{8}\)
= \(\frac{72}{1}\) × \(\frac{5}{8}\)
= \(\frac{72 × 5}{1 × 8}\)
= 45 sedimentary rocks
The number of rocks that are igneous = ( The total number of rocks ) × ( The fraction of rocks that are igneous )
= 72 × \(\frac{1}{6}\)
= \(\frac{72}{1}\) × \(\frac{1}{6}\)
= \(\frac{72 × 1}{1 × 6}\)
= 12 igneous rocks
So,
The number of metamorphous rocks = ( The total number of rocks ) – ( The number of sedimentary rocks + The number of igneous rocks)
= 72 – ( 45 + 12 )
= 15 metamorphous rocks
Hence, from the above,
We can conclude that there are 15 metamorphous rocks
Question 18.
DIG DEEPER!
Each day, you spend \(\frac{3}{4}\) hour reading and \(\frac{1}{2}\) hour writing in a journal. How many total hours do you spend reading and writing in 1 week? Describe two ways to solve the problem.

Answer:
The number of hours you spend on reading and writing in 1 week is:
Explanation:
It is given that, each day you spent \(\frac{3}{4}\) hour reading and \(\frac{1}{2}\) hour writing in a journal.
So,
The number of hours you spent on reading and writing a journal in 1 day = ( The number of hours spent on reading ) + ( The number of hours spent on writing )
= \(\frac{3}{4}\) + \(\frac{1}{2}\)
Multiply \(\frac{1}{2}\) with \(\frac{2}{2}\)
So,
\(\frac{3}{4}\) + \(\frac{2}{4}\)
= \(\frac{3 + 2}{4}\)
= \(\frac{5}{4}\) hours
We know that,
1 day = 24 hours
1 week = 7 days
So,
1 week = 7 × 24 hours
So,
The number of hours you spent on reading and writing in 1 week = ( The number of hours you spent on reading and writing in 1 day ) × ( The number of hours in 1 week )
= \(\frac{5}{4}\) × 7 × 24
= \(\frac{5}{4}\) × \(\frac{7}{1}\) × \(\frac{24}{1}\)
= \(\frac{5 × 7 × 24}{4 × 1}\)
= 5 × 7 × 6
= 210 hours
Hence, from the above,
We can conclude that the number of hours you spent on reading and writing a journal in 1 week is: 210 hours
Multiply Fractions and Whole Numbers Homework & Practice 9.3
Multiply.
Question 1.
\(\frac{5}{6}\) × 3 = _______
Answer:
3 × \(\frac{5}{6}\) = \(\frac{5}{2}\)
Explanation:
The given numbers are: 3 and \(\frac{5}{6}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
3 × \(\frac{5}{6}\) = \(\frac{3}{1}\) × \(\frac{5}{6}\)
= \(\frac{3 × 5}{6 × 1}\)
= \(\frac{5}{6}\)
= \(\frac{5}{2}\)
Hence,
3 × \(\frac{5}{6}\) = \(\frac{5}{2}\)
Question 2.
\(\frac{2}{3}\) × 6 = _______
Answer:
6 × \(\frac{2}{3}\) = 4
Explanation:
The given numbers are: 6 and \(\frac{2}{3}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
6 × \(\frac{2}{3}\) = \(\frac{6}{1}\) × \(\frac{2}{3}\)
= \(\frac{6 × 2}{3 × 1}\)
= \(\frac{12}{3}\)
= \(\frac{4}{1}\)
= 4
Hence,
6 × \(\frac{2}{3}\) = 4
Question 3.
7 × \(\frac{1}{8}\) = _______
Answer:
7 × \(\frac{1}{8}\) = \(\frac{7}{8}\)
Explanation:
The given numbers are: 7 and \(\frac{1}{8}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
7 × \(\frac{1}{8}\) = \(\frac{7}{1}\) × \(\frac{1}{8}\)
= \(\frac{7 × 1}{8 × 1}\)
= \(\frac{7}{8}\)
Hence,
7 × \(\frac{1}{8}\) = \(\frac{7}{8}\)
Question 4.
2 × \(\frac{1}{2}\) = _______
Answer:
2 × \(\frac{1}{2}\) = 1
Explanation:
The given numbers are: 2 and \(\frac{1}{2}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
2 × \(\frac{1}{2}\) = \(\frac{2}{1}\) × \(\frac{1}{2}\)
= \(\frac{2 × 1}{2 × 1}\)
= \(\frac{2}{2}\)
= 1
Hence,
2 × \(\frac{1}{2}\) = 1
Question 5.
\(\frac{4}{5}\) × 9 = _______
Answer:
9 × \(\frac{4}{5}\) = \(\frac{36}{5}\)
Explanation:
The given numbers are: 9 and \(\frac{4}{5}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
9 × \(\frac{4}{5}\) = \(\frac{9}{1}\) × \(\frac{4}{5}\)
= \(\frac{9 × 4}{5 × 1}\)
= \(\frac{36}{5}\)
Hence,
9 × \(\frac{4}{5}\) = \(\frac{36}{5}\)
Question 6.
4 × \(\frac{5}{12}\) = _______
Answer:
4 × \(\frac{5}{12}\) = \(\frac{5}{3}\)
Explanation:
The given numbers are: 4 and \(\frac{5}{12}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
4 × \(\frac{5}{12}\) = \(\frac{4}{1}\) × \(\frac{5}{12}\)
= \(\frac{4 × 5}{12 × 1}\)
= \(\frac{20}{12}\)
= \(\frac{5}{3}\)
Hence,
4 × \(\frac{5}{12}\) = \(\frac{5}{3}\)
Question 7.
\(\frac{1}{4}\) × 24 = _______
Answer:
24 × \(\frac{1}{24}\) = 6
Explanation:
The given numbers are: 24 and \(\frac{1}{4}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
24 × \(\frac{1}{4}\) = \(\frac{24}{1}\) × \(\frac{1}{4}\)
= \(\frac{24 × 1}{4 × 1}\)
= \(\frac{24}{4}\)
= 6
Hence,
24 × \(\frac{1}{4}\) = 6
Question 8.
16 × \(\frac{3}{8}\) = _______
Answer:
16 × \(\frac{3}{8}\) = 6
Explanation:
The given numbers are: 16 and \(\frac{3}{8}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
16 × \(\frac{3}{8}\) = \(\frac{16}{1}\) × \(\frac{3}{8}\)
= \(\frac{16 × 3}{8 × 1}\)
= \(\frac{48}{8}\)
= 6
Hence,
16 × \(\frac{3}{8}\) = 6
Question 9.
\(\frac{7}{10}\) × 25 = _______
Answer:
25 × \(\frac{7}{10}\) = \(\frac{35}{2}\)
Explanation:
The given numbers are: 25 and \(\frac{7}{10}\)
We know that,
\(\frac{a}{b}\) × p = \(\frac{a}{b}\) × \(\frac{p}{1}\)
= \(\frac{a × p}{ b × 1}\)
p = \(\frac{p}{1}\)
So,
25 × \(\frac{7}{10}\) = \(\frac{25}{1}\) × \(\frac{7}{10}\)
= \(\frac{7 × 25}{10 × 1}\)
= \(\frac{175}{10}\)
= \(\frac{35}{2}\)
Hence,
25 × \(\frac{7}{10}\) = \(\frac{35}{2}\)
Question 10.
You spend \(\frac{3}{4}\) hour jumping rope every week for 8 weeks. How many hours do you jump rope altogether?

Answer:
The number of hours you jump rope altogether in 8 weeks is: 6 hours
Explanation:
It is given that you spent \(\frac{3}{4}\) hour jumping rope every week for 8 weeks.
So,
The number of hours you spent jumping rope in 8 weeks = ( The number of hours you jump rope in 1 week ) × ( The total number of weeks )
= \(\frac{3}{4}\) × 8
= \(\frac{3}{4}\) × \(\frac{8}{1}\)
= \(\frac{3 × 8}{4 × 1}\)
= 6 hours
hence, from the above,
We can conclude that you spent 6 hours on jumping rope in 8 weeks.
Question 11.
Logic
Your friend finds 25 items that are either insects or flowers. She says that \(\frac{1}{6}\) of the items are insects. Can this be true? Explain.
Answer:
No, this is not true
Explanation:
It is given that your friend finds 25 items that are either insects or flowers and she says that \(\frac{1}{6}\) of the items are insects.
But,
The number of either insects or flowers will always be a whole number.
But, from the given information,
25 will not be divided by \(\frac{1}{6}\)
So,
The statement “\(\frac{1}{6}\) of the items are insects” is false.
Question 12.
Open-Ended
Write two different pairs of fractions that could represent the insects and flowers your friend finds in Exercise 11.
Answer:
The different pairs of fractions that could represent the insects and flowers are:
\(\frac{1}{5}\) and \(\frac{1}{25}\)
Explanation:
These different pairs of fractions have to divide 25
So,
We have to take the fractions the multiples of 5 i.e., 5 and 25
Hence, from the above,
We can conclude that
The different pairs of fractions that could represent the insects and flowers are:
\(\frac{1}{5}\) and \(\frac{1}{25}\)
Question 13.
Modeling Real Life
Newton bakes 56 treats. Five-eighths of them contains peanut butter. Descartes bakes 120 treats. Five-sixths of them contain peanut butter. Who bakes more peanut butter treats? How many more?

Answer:
Descartes bakes more peanut butter treats
The number of peanut butter treats Descartes made more than Descartes is: 65
Explanation:
It is given that Newton bakes 56 treats and five-eights of them contains peanut butter
So,
The number of peanut butter treats made by Newton = \(\frac{5}{8}\) × 56
= \(\frac{5}{8}\) × \(\frac{56}{1}\)
= \(\frac{5 × 56}{8 × 1}\)
= 35 peanut butter treats
It is also given that Descartes bakes 120 treats and five-sixths of them contain peanut butter
So,
the number of peanut butter treats made by Descartes = \(\frac{5}{6}\) × 120
= \(\frac{5}{6}\) × \(\frac{120}{1}\)
= \(\frac{5 × 120}{6 × 1}\)
= 100 peanut butter treats
So,
In the comparison of peanut butter treats,
Descartes bakes more
Now,
The number of peanut butter treats baked by Descartes more than Newton = 100 – 35
= 65 peanut butter treats
Hence, from the above,
We can conclude that
Descartes bakes more peanut butter treats
The number of peanut butter treats Descartes made more than Descartes is: 65
Question 14.
Modeling Real Life
Your class conducts an egg-dropping experiment with 60 eggs. Three-fifths of the eggs break open, one-sixth of the eggs crack, and the rest do not break at all. How many of the eggs do not crack or break open?
Answer:
The number of eggs that do not break is:
Explanation:
It is given that your class conducts an egg-dropping experiment with 60 eggs and three-fifths of the eggs break open, one-sixth of the eggs crack and the rest do not break.
So,
The number of eggs that break open = 60 × \(\frac{3}{5}\)
= \(\frac{60}{1}\) × \(\frac{3}{5}\)
= 36
The number of eggs that cracked = 60 × \(\frac{1}{6}\)
= \(\frac{60}{1}\) × \(\frac{1}{6}\)
= 10
So,
The number of eggs that do not breaked = ( The total number of eggs ) – ( The number of eggs that break open + The number of eggs that cracked )
= 60 – ( 36 + 10 )
= 16
Hence, from the above,
We can conclude that the number of eggs that do not break is: 16 eggs
Review & Refresh
Add.
Question 15.
5\(\frac{5}{8}\) + 6\(\frac{3}{4}\) = _______
Answer:
5\(\frac{5}{8}\) + 6\(\frac{3}{4}\) = \(\frac{99}{8}\)
Explanation:
The give mixed fractions are: 6\(\frac{3}{4}\) and 5\(\frac{5}{8}\)
The representation of mixed fractions in the improper form is: \(\frac{45}{8}\) and \(\frac{27}{4}\)
In addition,
We have to make the denominators equal.
So,
Multiply \(\frac{27}{4}\) with \(\frac{2}{2}\)
So,
\(\frac{45}{8}\) + \(\frac{54}{8}\) = \(\frac{45 + 54}{8}\)
= \(\frac{99}{8}\)
Hence,
5\(\frac{5}{8}\) + 6\(\frac{3}{4}\) = \(\frac{99}{8}\)
Question 16.
1\(\frac{5}{6}\) + 8\(\frac{1}{12}\) = ________
Answer:
1\(\frac{5}{6}\) + 8\(\frac{1}{12}\) = \(\frac{119}{12}\)
Explanation:
The give mixed fractions are: 1\(\frac{5}{6}\) and 8\(\frac{1}{12}\)
The representation of mixed fractions in the improper form is: \(\frac{11}{6}\) and \(\frac{97}{12}\)
In addition,
We have to make the denominators equal.
So,
Multiply \(\frac{11}{6}\) with \(\frac{2}{2}\)
So,
\(\frac{97}{12}\) + \(\frac{22}{12}\) = \(\frac{97 + 22}{12}\)
= \(\frac{119}{12}\)
Hence,
1\(\frac{5}{6}\) + 8\(\frac{1}{12}\) = \(\frac{119}{12}\)
Question 17.
3\(\frac{1}{2}\) + \(\frac{3}{5}\) + 2\(\frac{7}{10}\) = _______
Answer:
3\(\frac{1}{2}\) + 2\(\frac{7}{10}\) + \(\frac{3}{5}\) = \(\frac{68}{10}\)
Explanation:
The give mixed fractions are: 3\(\frac{1}{2}\), \(\frac{3}{5}\) and 2\(\frac{7}{10}\)
The representation of mixed fractions in the improper form is: \(\frac{7}{2}\) and \(\frac{27}{10}\)
In addition,
We have to make the denominators equal.
So,
Multiply \(\frac{7}{2}\) with \(\frac{5}{5}\)
Multiply \(\frac{3}{5}\) with \(\frac{2}{2}\)
So,
\(\frac{27}{10}\) + \(\frac{35}{10}\) + \(\frac{6}{10}\) = \(\frac{27 + 35 + 6}{10}\)
= \(\frac{68}{10}\)
Hence,
3\(\frac{1}{2}\) + 2\(\frac{7}{10}\) + \(\frac{3}{5}\) = \(\frac{68}{10}\)
Lesson 9.4 Use Models to Multiply Fractions
Explore and Grow
Fold a sheet of paper in half. Shade \(\frac{1}{4}\) of either half. What fraction of the entire sheet of paper did you shade? Draw a model to support your answer.
Answer:
The fraction of the entire sheet of paper you shaded is: \(\frac{1}{8}\)
Explanation:
Take a full sheet of paper and fold in half
So,
The number of parts of full sheet of paper = \(\frac{1}{2}\)
Now,
Shade \(\frac{1}{4}\) of the half of the paper
So,,
The fraction of the paper you shaded = \(\frac{1}{4}\) × \(\frac{1}{2}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{2}\)
= \(\frac{1 × 1}{4 × 2}\)
= \(\frac{1}{8}\)
Hence, from the above,
We can conclude that the \(\frac{1}{8}\) part of the full sheet is shaded
Reasoning
What multiplication expression does your model represent? Explain your reasoning.
Answer:
The multiplication expression your model represents is: \(\frac{1}{8}\)
We can obtain the multiplication expression by using the following multiplication properties. They are:
A) \(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
B) a = \(\frac{a}{1}\)
Think and Grow: Use Models to Multiply Fractions
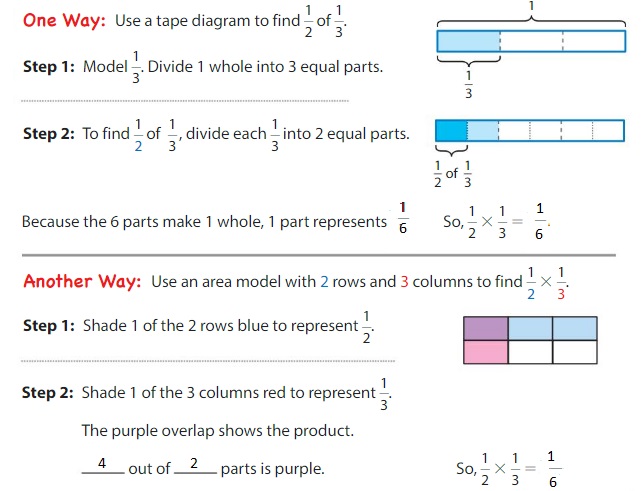
You can use models to multiply a fraction by a fraction.
Example
Find \(\frac{1}{2}\) × \(\frac{1}{3}\).
Show and Grow
Multiply. Use a model to help.
Question 1.
\(\frac{1}{3}\) × \(\frac{1}{4}\) = _______
Answer:
\(\frac{1}{3}\) × \(\frac{1}{4}\) = \(\frac{1}{12}\)
Explanation:
The given fractions are: \(\frac{1}{4}\) and \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{3}\)
= \(\frac{1 × 1}{4 × 3}\)
= \(\frac{1}{12}\)
Hence,
\(\frac{1}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{12}\)
Question 2.
\(\frac{2}{3}\) × \(\frac{1}{2}\) = _______
Answer:
\(\frac{2}{3}\) × \(\frac{1}{2}\) = \(\frac{1}{3}\)
Explanation:
The given fractions are: \(\frac{2}{3}\) and \(\frac{1}{2}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{2}\) × \(\frac{2}{3}\)
= \(\frac{1 × 2}{2 × 3}\)
= \(\frac{1}{3}\)
Hence,
\(\frac{1}{2}\) × \(\frac{2}{3}\) = \(\frac{1}{3}\)
Apply and Grow: Practice
Multiply. Use a model to help.
Question 3.
\(\frac{1}{2}\) × \(\frac{1}{6}\) = _______
Answer:
\(\frac{1}{2}\) × \(\frac{1}{6}\) = \(\frac{1}{12}\)
Explanation:
The given fractions are: \(\frac{1}{2}\) and \(\frac{1}{6}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{2}\) × \(\frac{1}{6}\)
= \(\frac{1 × 1}{2 × 6}\)
= \(\frac{1}{12}\)
Hence,
\(\frac{1}{2}\) × \(\frac{1}{6}\) = \(\frac{1}{12}\)
Question 4.
\(\frac{1}{5}\) × \(\frac{1}{8}\) = _______
Answer:
\(\frac{1}{5}\) × \(\frac{1}{8}\) = \(\frac{1}{40}\)
Explanation:
The given fractions are: \(\frac{1}{5}\) and \(\frac{1}{8}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{5}\) × \(\frac{1}{8}\)
= \(\frac{1 × 1}{5 × 8}\)
= \(\frac{1}{40}\)
Hence,
\(\frac{1}{5}\) × \(\frac{1}{8}\) = \(\frac{1}{40}\)
Question 5.
\(\frac{1}{4}\) × \(\frac{1}{6}\) = _______
Answer:
\(\frac{1}{4}\) × \(\frac{1}{6}\) = \(\frac{1}{24}\)
Explanation:
The given fractions are: \(\frac{1}{4}\) and \(\frac{1}{6}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{6}\)
= \(\frac{1 × 1}{4 × 6}\)
= \(\frac{1}{24}\)
Hence,
\(\frac{1}{4}\) × \(\frac{1}{6}\) = \(\frac{1}{24}\)
Question 6.
\(\frac{2}{3}\) × \(\frac{1}{3}\) = _______
Answer:
\(\frac{2}{3}\) × \(\frac{1}{3}\) = \(\frac{2}{9}\)
Explanation:
The given fractions are: \(\frac{2}{3}\) and \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{2}{3}\) × \(\frac{1}{3}\)
= \(\frac{2 × 1}{3 × 3}\)
= \(\frac{2}{9}\)
Hence,
\(\frac{2}{3}\) × \(\frac{1}{3}\) = \(\frac{2}{9}\)
Write a multiplication equation represented by the model.
Question 7.
Answer:
The multiplication equation represented by the model is:
\(\frac{1}{2}\) × \(\frac{1}{8}\)
Explanation:
The given model is:

From the above model,
The number of rows is: 2
The number of columns is: 8
So,
The value of 1 row = \(\frac{1}{2}\)
The value of 1 column = \(\frac{1}{8}\)
So,
Rows × Columns = \(\frac{1}{8}\) × \(\frac{1}{2}\)
Hence, from the above,
We can conclude that the multiplication equation represented by the above model is:
\(\frac{1}{8}\) × \(\frac{1}{2}\)
Question 8.
Answer:
The multiplication equation represented by the model is:
\(\frac{1}{4}\) × \(\frac{1}{5}\)
Explanation:
The given model is:

From the above model,
The number of rows is: 4
The number of columns is: 5
So,
The value of 1 row = \(\frac{1}{4}\)
The value of 1 column = \(\frac{1}{5}\)
So,
Rows × Columns = \(\frac{1}{4}\) × \(\frac{1}{5}\)
Hence, from the above,
We can conclude that the multiplication equation represented by the above model is:
\(\frac{1}{4}\) × \(\frac{1}{5}\)
Question 9.
One-fifth of the students in your school have tried skating. Of those students, \(\frac{1}{7}\) have tried ice skating. What fraction of students in your school have tried ice skating?
Answer:
The fraction of students that have tried ice skating is: \(\frac{1}{35}\)
Explanation:
It is given that one-fifth of the students in your school have tried skating and of these students, \(\frac{1}{7}\) have tried ice skating
So,
The fraction of students that have tried ice skating = ( The fraction of students that have tried skating ) × ( The fraction of students that tried ice skating out of the total students )
= \(\frac{1}{5}\) × \(\frac{1}{7}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{5}\) × \(\frac{1}{7}\)
= \(\frac{1 × 1}{5 × 7}\)
= \(\frac{1}{35}\)
Hence, from the above,
We can conclude that \(\frac{1}{35}\) of the total students tried ice skating.
Question 10.
DIG DEEPER!
Are both Newton and Descartes correct? Explain.

Answer: Yes, both Newton and Descartes are correct.
Explanation:
The given models of Newton and Descartes are:

From the model of Newton,
The number of rows is: 3
The number of columns is: 5
From the model of Descartes,
The number of rows is: 5
The number of columns is: 3
From the above models,
We can observe that the Descartes model is obtained by reversing the rows and columns of Newton i.e., the rows of Newton’s model become the columns of Descartes’s model and the columns of Newton’s model becomes the rows of Descartes’ model.
So,
The multiplication equation represented by Newton is:
\(\frac{1}{3}\) × \(\frac{1}{5}\)
The multiplication equation represented by Descartes is:
\(\frac{1}{5}\) × \(\frac{1}{3}\)
Hence, from the above,
We can conclude that Newton and Descartes are correct
Think and Grow: Modeling Real Life
Example
A recipe calls for \(\frac{3}{4}\) teaspoon of cinnamon. You4want to halve the recipe. What fraction of a teaspoon of cinnamon do you need?

Because you want to halve the recipe, multiply \(\frac{1}{2}\) by \(\frac{3}{4}\) to find how many teaspoons of cinnamon you need.

So,
You need \(\frac{3}{8}\) teaspoon of cinnamon.
Show and Grow
Question 11.
The mass of mango is \(\frac{2}{5}\) kilogram. The mass of guava is \(\frac{1}{4}\) as much as the mango. What is the mass of the guava?

Answer:
The mass of guava is: \(\frac{1}{10}\) kilograms
Explanation:
It is given that the mass of mango is \(\frac{2}{5}\) kilogram and the mass of guava is \(\frac{1}{4}\) as much as the mango.
So,
The mass of guava = ( The mass of mango ) × ( The fraction of mass of guava in the mass of mango )
= \(\frac{2}{5}\) × \(\frac{1}{4}\)
= \(\frac{1 × 2}{4 × 5}\)
= \(\frac{2}{20}\)
= \(\frac{1}{10}\) kilograms
Hnce, from the above,
We can conclude that the mass of guava is: \(\frac{1}{10}\) kilogram
Question 12.
A giant panda spends \(\frac{2}{3}\) of 1-day eating and foraging. It spends \(\frac{3}{4}\) of that time for eating bamboo. What fraction of 1 day does the panda spend eating bamboo?
Answer:
The fraction of 1 day the panda spent on eating bamboo is: \(\frac{1}{2}\)
Explanation:
It is given that a giant panda spends \(\frac{2}{3}\) of 1-day eating and foraging and it spends \(\frac{3}{4}\) of that time for eating bamboo.
So,
The fraction of 1 day the panda spent on eating bamboo = ( The fraction of time the panda spent on eating ) × ( The fraction of time the panda spent time on eating bamboo out of the total time )
= \(\frac{2}{3}\) × \(\frac{3}{4}\)
= \(\frac{3 × 2}{4 × 3}\)
= \(\frac{6}{12}\)
= \(\frac{1}{2}\) hour
Hence, from the above,
We can conclude that the time spent by the panda on eating bamboo is: \(\frac{1}{2}\) hour
Question 13.
DIG DEEPER!
You have a half-gallon carton of milk that you use only for cereal. You use the same amount each day for 5 days. There is \(\frac{3}{8}\) of the carton left. How many cups of milk do you use each day? Explain.
Answer:
Use Models to Multiply Fractions Homework & Practice 9.4
Multiply. Use a model to help.
Question 1.
\(\frac{1}{3}\) × \(\frac{1}{7}\) = _______
Answer:
\(\frac{1}{3}\) × \(\frac{1}{7}\) = \(\frac{1}{21}\)
Explanation:
The given fractions are: \(\frac{1}{7}\) and \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{7}\) × \(\frac{1}{3}\)
= \(\frac{1 × 1}{7 × 3}\)
= \(\frac{1}{21}\)
Hence,
\(\frac{1}{7}\) × \(\frac{1}{3}\) = \(\frac{1}{21}\)
Question 2.
\(\frac{1}{2}\) × \(\frac{1}{9}\) = _______
Answer:
\(\frac{1}{2}\) × \(\frac{1}{9}\) = \(\frac{1}{18}\)
Explanation:
The given fractions are: \(\frac{1}{2}\) and \(\frac{1}{9}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{2}\) × \(\frac{1}{9}\)
= \(\frac{1 × 1}{2 × 9}\)
= \(\frac{1}{18}\)
Hence,
\(\frac{1}{2}\) × \(\frac{1}{9}\) = \(\frac{1}{18}\)
Question 3.
\(\frac{2}{5}\) × \(\frac{1}{6}\) = _______
Answer:
\(\frac{2}{5}\) × \(\frac{1}{6}\) = \(\frac{1}{15}\)
Explanation:
The given fractions are: \(\frac{2}{5}\) and \(\frac{1}{6}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{2}{5}\) × \(\frac{1}{6}\)
= \(\frac{2 × 1}{5 × 6}\)
= \(\frac{1}{15}\)
Hence,
\(\frac{2}{5}\) × \(\frac{1}{6}\) = \(\frac{1}{15}\)
Question 4.
\(\frac{3}{4}\) × \(\frac{2}{7}\) = _______
Answer:
\(\frac{3}{4}\) × \(\frac{2}{7}\) = \(\frac{3}{14}\)
Explanation:
The given fractions are: \(\frac{3}{4}\) and \(\frac{2}{7}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\) = \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{3}{4}\) × \(\frac{2}{7}\)
= \(\frac{3 × 2}{4 × 7}\)
= \(\frac{3}{14}\)
Hence,
\(\frac{3}{4}\) × \(\frac{2}{7}\) = \(\frac{3}{14}\)
Write a multiplication equation represented by the model.
Question 5.
Answer:
The multiplication equation represented by the model is:
\(\frac{1}{2}\) × \(\frac{1}{5}\)
Explanation:
The given model is:

From the above model,
The number of rows is: 2
The number of columns is: 5
So,
The value of 1 row = \(\frac{1}{2}\)
The value of 1 column = \(\frac{1}{5}\)
So,
Rows × Columns = \(\frac{1}{2}\) × \(\frac{1}{5}\)
Hence, from the above,
We can conclude that the multiplication equation represented by the above model is:
\(\frac{1}{2}\) × \(\frac{1}{5}\)
Question 6.
Answer:
The multiplication equation represented by the model is:
\(\frac{1}{3}\) × \(\frac{1}{6}\)
Explanation:
The given model is:

From the above model,
The number of rows is: 3
The number of columns is: 6
So,
The value of 1 row = \(\frac{1}{3}\)
The value of 1 column = \(\frac{1}{6}\)
So,
Rows × Columns = \(\frac{1}{3}\) × \(\frac{1}{6}\)
Hence, from the above,
We can conclude that the multiplication equation represented by the above model is:
\(\frac{1}{3}\) × \(\frac{1}{6}\)
Question 7.
One-sixth of the animals at a zoo are birds. Of the birds, \(\frac{1}{3}\) are female. What fraction of the animals at the zoo are female birds?
Answer:
The fraction of the animals at the zoo that is female birds is: \(\frac{1}{18}\)
Explanation:
It is given that one-sixth of the animals at the zoo are birds and of the birds, \(\frac{1}{3}\) is female.
So,
The fraction of the animals at the zoo are female birds = ( The fraction of animals in the zoo that is birds ) × ( The fraction of the animals in the zoo that is female birds )
= \(\frac{1}{3}\) × \(\frac{1}{6}\)
\(\frac{1 × 1}{3 × 6}\)
= \(\frac{1}{18}\)
Hence, from the above,
We can conclude that the number of animals that are female birds at the zoo is: \(\frac{1}{18}\)
Question 8.
Writing
Write and solve a real-life problem for the expression.
\(\frac{2}{3}\) × \(\frac{3}{7}\)
Answer:
Suppose in a school, there are boys ad girls.
In school, \(\frac{2}{3}\) of the boys and \(\frac{3}{7}\) of the girls passed the PET test
So,
The fraction of the students that passed the PET test out of the total number of students = ( The fraction of the boys that passed the PET test ) × ( The fraction of the girls that passed the PET test )
= \(\frac{2}{3}\) × \(\frac{3}{7}\)
= \(\frac{3 × 2}{7 × 3}\)
= \(\frac{6}{21}\)
= \(\frac{2}{7}\)
Hence, from the above,
We can conclude that the number of students who passed the PET test is: \(\frac{2}{7}\)
Question 9.
Modeling Real Life
A Gouldian finch is \(\frac{1}{2}\) the length of the sun conure. How long is the Gouldian finch?
Answer:
The length of Gouldian finch is: \(\frac{11}{24}\) feet
Explanation:
It is given that a Gouldian finch is \(\frac{1}{2}\) the length of the sun conure.
From the given figure,
The length of the sun conure = \(\frac{11}{12}\) feet
So,
The length of Gouldian finch = ( The length of Sun Conure ) ÷ 2
= \(\frac{11}{12}\) ÷ 2
= \(\frac{11}{12}\) ÷ \(\frac{2}{1}\)
= \(\frac{11}{12}\) × \(\frac{1}{2}\)
= \(\frac{11 × 1}{12 × 2}\)
= \(\frac{11}{24}\) feet
Hence, from the above,
We can conclude that the length of the Gouldian finch is: \(\frac{11}{24}\) feet
Question 10.
DIG DEEPER!
A recipe calls for \(\frac{2}{3}\) cup of chopped walnuts. You chop 4 walnuts and get \(\frac{1}{4}\) of the amount you need. How much more of a cup of chopped walnuts do you need? All of your walnuts are the same size. How many more walnuts should you chop? Explain.
Answer:
The cup of chopped walnuts more you need is: \(\frac{1}{3}\)
The number of walnuts you should chop is: 6
Explanation:
It is given that a recipe calls for \(\frac{2}{3}\) cup of chopped walnuts.
It is also given that you chop 4 walnuts and get \(\frac{1}{4}\) of the amount you need.
So,
The cup more of chopped walnuts you need = 1- ( The cup of chopped walnuts you need for recipe )
= 1 – \(\frac{2}{3}\)
= \(\frac{3}{3}\) – \(\frac{2}{3}\)
= \(\frac{3 – 2}{3}\)
= \(\frac{1}{3}\) more cup
Now,
The number of walnuts you need more = ( The number of walnuts you needed to get \(\frac{1}{4}\) of cup of chopped walnuts ) ÷ ( The amount of chopped walnuts you need for recipe )
= 4 ÷ \(\frac{2}{3}\)
= \(\frac{4}{1}\) ÷ \(\frac{2}{3}\)
= \(\frac{4}{1}\) × \(\frac{3}{2}\)
= \(\frac{4 × 3}{1 × 2}\)
= \(\frac{12}{2}\)
= 6
Hence, from the above,
We can conclude that
The cup of chopped walnuts more you need is: \(\frac{1}{3}\)
The number of walnuts you should chop is: 6
Review & Refresh
Subtract.
Question 11.
5 – 1\(\frac{3}{4}\) = ______
Answer:
5 – 1\(\frac{3}{4}\) = \(\frac{13}{4}\)
Explanation:
The given numbers are: 5 and 1\(\frac{3}{4}\)
The representation of 1\(\frac{3}{4}\) in the improper fraction form is: \(\frac{7}{4}\)
So,
5 – \(\frac{7}{4}\) = \(\frac{20}{4}\) – \(\frac{7}{4}\)
= \(\frac{20 – 7}{4}\)
= \(\frac{13}{4}\)
Hence,
5 – 1\(\frac{3}{4}\) = \(\frac{13}{4}\)
Question 12.
13\(\frac{1}{4}\) – 7\(\frac{5}{8}\) = ________
Answer:
13\(\frac{1}{4}\) – 7\(\frac{5}{8}\) = \(\frac{45}{8}\)
Explanation:
The given mixed fractions are: 13\(\frac{1}{4}\) and 7\(\frac{5}{8}\)
The representation of 13\(\frac{1}{4}\) in the improper fraction form is: \(\frac{53}{4}\)
The representation of 13\(\frac{1}{4}\) in the improper fraction form is: \(\frac{61}{8}\)
To subtract the fractions, we have to make the denominators equal.
So,
Multiply \(\frac{53}{4}\) by \(\frac{2}{2}\)
So,
\(\frac{53}{4}\) = \(\frac{106}{8}\)
So,
\(\frac{106}{8}\) – \(\frac{61}{8}\)
= \(\frac{106 – 61}{8}\)
= \(\frac{45}{8}\)
Hence,
13\(\frac{1}{4}\) – 13\(\frac{1}{4}\) = \(\frac{45}{8}\)
Question 13.
12\(\frac{7}{10}\) – 5\(\frac{3}{10}\) – 1\(\frac{1}{5}\) = ________
Answer:
12\(\frac{7}{10}\) – 5\(\frac{3}{10}\) – 1\(\frac{1}{5}\) = \(\frac{62}{10}\)
Explanation:
The given mixed fractions are: 12\(\frac{7}{10}\), 5\(\frac{3}{10}\) and 1\(\frac{1}{5}\)
The representation of 12\(\frac{7}{10}\) in the improper fraction form is: \(\frac{127}{10}\)
The representation of 5\(\frac{3}{10}\) in the improper fraction form is: \(\frac{53}{10}\)
The representation of 1\(\frac{1}{5}\) in the improper fraction form is: \(\frac{6}{5}\)
To subtract the fractions, we have to make the denominators equal.
So,
Multiply \(\frac{6}{5}\) by \(\frac{2}{2}\)
So,
\(\frac{6}{5}\) = \(\frac{12}{10}\)
So,
\(\frac{127}{10}\) – \(\frac{53}{10}\) – \(\frac{12}{10}\)
= \(\frac{127 – 53 – 12}{8}\)
= \(\frac{62}{10}\)
Hence,
12\(\frac{7}{10}\) – 5\(\frac{3}{10}\) – 1\(\frac{1}{5}\) = \(\frac{62}{10}\)
Lesson 9.5 Multiply Fractions
Explore and Grow
Use models to help you complete the table. What do you notice about each expression and its product?

Answer:
The completed table is:
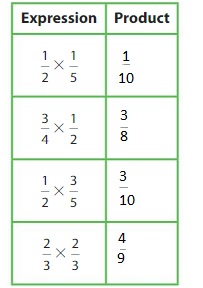
From the given table,
We can observe the product of fractions is also a product.
Construct Arguments
Explain how to multiply two fractions without using a model.
Answer:
We can multiply the fractions by using the properties of multiplication. They are:
A) \(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
B) a = \(\frac{a}{1}\)
Think and Grow: Multiply Fractions
Key Idea
You can find the product of a fraction and a fraction by multiplying the numerators and multiplying the denominators.
Example
Find \(\frac{1}{2}\) × \(\frac{3}{2}\).
Multiply the numerators and multiply the denominators.
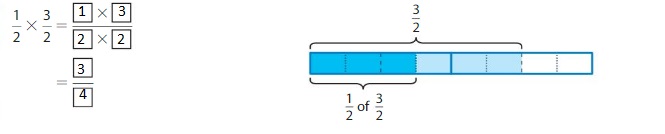
Example
Find \(\frac{5}{6}\) × \(\frac{3}{5}\).
Multiply the numerators and multiply the denominators.
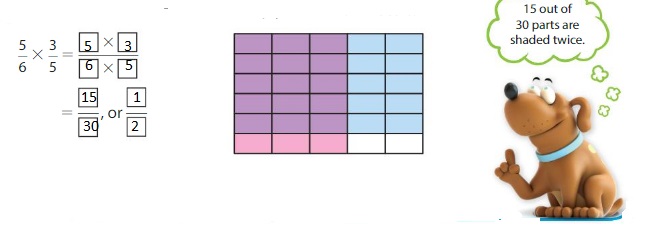
Show and Grow
Multiply.
Question 1.
\(\frac{1}{2}\) × \(\frac{4}{3}\) = _______
Answer:
\(\frac{1}{2}\) × \(\frac{4}{3}\) = \(\frac{2}{3}\)
Explanation:
The given fractions are: \(\frac{1}{2}\) and \(\frac{4}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{2}\) × \(\frac{4}{3}\)
= \(\frac{1 × 4}{2 × 3}\)
= \(\frac{4}{6}\)
= \(\frac{2}{3}\)
Hence,
\(\frac{1}{2}\) × \(\frac{4}{3}\) = \(\frac{2}{3}\)
Question 2.
\(\frac{2}{5}\) × \(\frac{2}{3}\) = _______
Answer:
\(\frac{2}{5}\) × \(\frac{2}{3}\) = \(\frac{4}{15}\)
Explanation:
The given fractions are: \(\frac{2}{5}\) and \(\frac{2}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{2}{5}\) × \(\frac{2}{3}\)
= \(\frac{2 × 2}{5 × 3}\)
= \(\frac{4}{15}\)
Hence,
\(\frac{2}{5}\) × \(\frac{2}{3}\) = \(\frac{4}{15}\)
Question 3.
\(\frac{3}{4}\) × \(\frac{5}{8}\) = _______
Answer:
\(\frac{3}{4}\) × \(\frac{5}{8}\) = \(\frac{15}{32}\)
Explanation:
The given fractions are: \(\frac{3}{4}\) and \(\frac{5}{8}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{3}{4}\) × \(\frac{5}{8}\)
= \(\frac{3 × 5}{4 × 8}\)
= \(\frac{15}{32}\)
Hence,
\(\frac{3}{4}\) × \(\frac{5}{8}\) = \(\frac{15}{32}\)
Apply and Grow: Practice
Multiply.
Question 4.
\(\frac{1}{4}\) × \(\frac{1}{4}\) = _______
Answer:
\(\frac{1}{4}\) × \(\frac{1}{4}\) = \(\frac{1}{16}\)
Explanation:
The given fractions are: \(\frac{1}{4}\) and \(\frac{1}{4}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{4}\)
= \(\frac{1 × 1}{4 × 4}\)
= \(\frac{1}{16}\)
Hence,
\(\frac{1}{4}\) × \(\frac{1}{4}\) = \(\frac{1}{16}\)
Question 5.
\(\frac{5}{6}\) × \(\frac{7}{10}\) = _______
Answer:
\(\frac{5}{6}\) × \(\frac{7}{10}\) = \(\frac{7}{12}\)
Explanation:
The given fractions are: \(\frac{5}{6}\) and \(\frac{7}{10}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{5}{6}\) × \(\frac{7}{10}\)
= \(\frac{5 × 7}{6 × 10}\)
= \(\frac{35}{60}\)
= \(\frac{7}{12}\)
Hence,
\(\frac{5}{6}\) × \(\frac{7}{10}\) = \(\frac{7}{12}\)
Question 6.
\(\frac{6}{9}\) × \(\frac{8}{2}\) = _______
Answer:
\(\frac{6}{9}\) × \(\frac{8}{2}\) = \(\frac{8}{3}\)
Explanation:
The given fractions are: \(\frac{6}{9}\) and \(\frac{8}{2}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{6}{9}\) × \(\frac{8}{2}\)
= \(\frac{6 × 8}{2 × 9}\)
= \(\frac{48}{18}\)
= \(\frac{8}{3}\)
Hence,
\(\frac{6}{9}\) × \(\frac{8}{2}\) = \(\frac{8}{3}\)
Question 7.
\(\frac{21}{100}\) × \(\frac{3}{5}\) = _______
Answer:
\(\frac{21}{100}\) × \(\frac{3}{5}\) = \(\frac{63}{500}\)
Explanation:
The given fractions are: \(\frac{21}{100}\) and \(\frac{3}{5}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{21}{100}\) × \(\frac{3}{5}\)
= \(\frac{21 × 3}{100 × 5}\)
= \(\frac{63}{500}\)
Hence,
\(\frac{21}{100}\) × \(\frac{3}{5}\) = \(\frac{63}{500}\)
Question 8.
\(\frac{1}{12}\) × \(\frac{9}{4}\) = _______
Answer:
\(\frac{1}{12}\) × \(\frac{9}{4}\) = \(\frac{3}{16}\)
Explanation:
The given fractions are: \(\frac{1}{12}\) and \(\frac{9}{4}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{12}\) × \(\frac{9}{4}\)
= \(\frac{1 × 9}{12 × 4}\)
= \(\frac{9}{48}\)
= \(\frac{3}{16}\)
Hence,
\(\frac{1}{12}\) × \(\frac{9}{4}\) = \(\frac{3}{16}\)
Question 9.
\(\frac{4}{7}\) × \(\frac{8}{8}\) = _______
Answer:
\(\frac{4}{7}\) × \(\frac{8}{8}\) = \(\frac{4}{7}\)
Explanation:
The given fractions are: \(\frac{4}{7}\) and \(\frac{8}{8}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{4}{7}\) × \(\frac{8}{8}\)
= \(\frac{8 × 4}{7 × 8}\)
= \(\frac{4}{7}\)
Hence,
\(\frac{4}{7}\) × \(\frac{8}{8}\) = \(\frac{4}{7}\)
Evaluate
Question 10.
\(\left(\frac{1}{2} \times \frac{7}{8}\right)\) × 2 = _______
Answer:
\(\left(\frac{1}{2} \times \frac{7}{8}\right)\) × 2 = \(\frac{7}{8}\)
Explanation:
The given fractions are: \(\frac{7}{8}\) and \(\frac{1}{2}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
( \(\frac{1}{2}\) × \(\frac{7}{8}\) ) × 2
= ( \(\frac{1 × 7}{2 × 8}\) ) × \(\frac{2}{1}\)
= \(\frac{7}{16}\) × \(\frac{2}{1}\)
= \(\frac{7 × 2}{16 × 1}\)
= \(\frac{7}{8}\)
Hence,
\(\frac{4}{7}\) × \(\frac{8}{8}\) = \(\frac{4}{7}\)
Question 11.
\(\left(\frac{7}{6}-\frac{5}{6}\right)\) × \(\frac{2}{3}\) = _______
Answer:
\(\left(\frac{7}{6}-\frac{5}{6}\right)\) × \(\frac{2}{3}\) = \(\frac{2}{9}\)
Explanation:
The given fractions are: \(\frac{7}{6}\) , \(\frac{5}{6}\), and \(\frac{2}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
( \(\frac{7}{6}\) – \(\frac{5}{6}\) ) × \(\frac{2}{3}\)
= ( \(\frac{7 – 5}{6}\) ) × \(\frac{2}{3}\)
= \(\frac{2}{6}\) × \(\frac{2}{3}\)
= \(\frac{2 × 2}{6 × 3}\)
= \(\frac{4}{18}\)
= \(\frac{2}{9}\)
Hence,
\(\left(\frac{7}{6}-\frac{5}{6}\right)\) × \(\frac{2}{3}\) = \(\frac{2}{9}\)
Question 12.
\(\frac{9}{10}\) × \(\left(\frac{4}{9}+\frac{1}{3}\right)\) = _________
Answer:
\(\frac{9}{10}\) × \(\left(\frac{4}{9}+\frac{1}{3}\right)\) = \(\frac{7}{10}\)
Explanation:
The given fractions are: \(\frac{9}{10}\), \(\frac{4}{9}\) and \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{9}{10}\) × ( \(\frac{4}{9}\) + \(\frac{1}{3}\) )
= ( \(\frac{4 + 3}{9}\) ) × \(\frac{9}{10}\)
= \(\frac{7}{9}\) × \(\frac{9}{10}\)
= \(\frac{7 × 9}{9 × 10}\)
= \(\frac{7}{10}\)
Hence,
\(\frac{9}{10}\) × \(\left(\frac{4}{9}+\frac{1}{3}\right)\) = \(\frac{7}{10}\)
Question 13.
At a school, \(\frac{3}{4}\) of the students play a sport. Of the students that play a sport, \(\frac{1}{5}\) play baseball. What fraction of the students at the school play baseball?

Answer:
The fraction of the students at the school that play baseball is: \(\frac{3}{20}\)
Explanation:
It is given that at a school, \(\frac{3}{4}\) of the students play a sport and of the students that play a sport, \(\frac{1}{5}\) play baseball.
So,
The fraction of the students at the school that play baseall = ( The fraction of the students that play a sport ) × ( The fraction of the students that play baseball out of thetotal number of students )
= \(\frac{3}{4}\) × \(\frac{1}{5}\)
= \(\frac{3 × 1}{4 × 5}\)
= \(\frac{3}{20}\)
Hence, from the above,
We can conclude that the fraction of the students that play baseball is: \(\frac{3}{20}\)
Question 14.
Reasoning
Descartes says he can find the product of a whole number and a fraction the same way he finds the product of two fractions. Explain why his reasoning makes sense.
Answer:
The product of a whole number and a fraction follows the same procedure as that of the product of the two fractions because of the following properties of multiplication:
A) \(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
B) a= \(\frac{a}{1}\)
Hence, from the above two properties of multiplication,
We can conclude that the reasoning of Descartes makes sense
Question 15.
Writing
Explain how multiplying fractions is different than adding and subtracting fractions.
Answer:
In the multiplication of the fractions, we multiply numerators and denominators.
Example:
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
In addition of the fractions, we add only numerators making the denominators equal
Example:
\(\frac{a}{b}\) + \(\frac{p}{b}\)
= \(\frac{a + p}{b}\)
In subtraction of the fractions, we subtract only numerators making the denominators equal
Example:
\(\frac{a}{b}\) – \(\frac{p}{b}\)
= \(\frac{a – p}{b}\)
Think and Grow: Modeling Real Life
Example
A tourist is walking from the Empire State Building to Times Square. She is \(\frac{2}{3}\) of the way there. What fraction of a mile does she have left to walk?
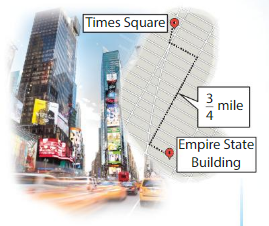
Find the distance she has walked. Because she has walked \(\frac{2}{3}\) of \(\frac{3}{4}\) mile, multiply \(\frac{2}{3}\) by \(\frac{3}{4}\).

Show and Grow
Question 16.
At a zoo, \(\frac{3}{5}\) of the animals are mammals. Of the mammals, \(\frac{5}{12}\) are primates.What fraction of the animals at the zoo are not primates?

Answer:
The fractions of the animals at the zoo that are not primates is: \(\frac{3}{4}\)
Explanation:
It is given that at the zoo, \(\frac{3}{5}\) of the animals are mammals and of the animals, \(\frac{5}{12}\) are primates
So,
The fraction of the animals that are primates =( The fraction of the animals that are primates ) × ( The fraction of the animals that are primates )
= \(\frac{3}{5}\) × \(\frac{5}{12}\)
= \(\frac{3 × 5}{5 × 12}\)
= \(\frac{15}{60}\)
= \(\frac{1}{4}\)
Now,
Let the total number of animals that are mammals =1
So,
The fraction of the animals that are not primates = ( The total number of mammals ) – ( The fraction of the animals that are primates )
= 1 – \(\frac{1}{4}\)
= \(\frac{4}{4}\) – \(\frac{1}{4}\)
= \(\frac{4 – 1}{4}\)
= \(\frac{3}{4}\)
Hence, from the above,
We can conclude that the fraction of the animals that are not primates is: \(\frac{3}{4}\)
Question 17.
You have an album of 216 trading cards. One page contains \(\frac{1}{24}\) of the cards. On that page, \(\frac{2}{3}\) of the cards are epic. You only have one page with any epic cards. How many epic cards do you have?
Answer:
The number of epic cards is: 6 epic cards
Explanation:
It is given that you have an album of 216 trading cards
It is also given that one page contains \(\frac{1}{24}\) of the cards. On that page, \(\frac{2}{3}\) of the cards are epic.
So,
The fraction of the epic cards = ( The total number of cards on that page ) × ( The fraction of the epic cards that is on that page )
= \(\frac{1}{24}\) × \(\frac{2}{3}\)
= \(\frac{2 × 1}{3 × 24}\)
= \(\frac{1}{36}\)
So,
The number of epic cards = ( The total number of cards ) × ( The fraction of the epic cards )
= 216 × \(\frac{1}{36}\)
= \(\frac{216}{1}\) × \(\frac{}{36}\)
= \(\frac{216}{36}\)
= 6 epic cards
Hence, from the above,
We can conclude that there are 6 epic cards
Question 18.
DIG DEEPER!
In a class, \(\frac{2}{5}\) of the students play basketball and \(\frac{7}{10}\) play soccer.Of the students who play basketball, \(\frac{2}{3}\) also play soccer. There are 30 students in the class. How many students play soccer but do not play basketball?
Answer:
The number of students that play soccer but do not play basketball is: 4 students
Explanation:
It is given that in a class, \(\frac{2}{5}\) of the students play basketball and \(\frac{7}{10}\) play soccer.Of the students who play basketball, \(\frac{2}{3}\) also play soccer.
So,
The number of students who play basketball and soccer = ( The number of students who play basketball ) × ( The number of students playing soccer who are also playing basketball )
= \(\frac{2}{5}\) × \(\frac{2}{3}\)
= \(\frac{4}{15}\)
Now,
The number of students who only play soccer but not basketball = ( The number of students who play soccer only ) – ( The number of students who play both basketball and soccer )
= \(\frac{2}{5}\) – \(\frac{4}{15}\)
In subtraction, the denominators must be equal.
So,
Multiply \(\frac{2}{5}\) by \(\frac{3}{3}\)
So,
\(\frac{6}{15}\) – \(\frac{4}{15}\)
= \(\frac{4}{15}\)
It is also given that the total number of students are: 30
So,
The number of students who play soccer only = ( The fraction of the students who play soccer only ) × ( The total number of students )
= \(\frac{2}{15}\) × 30
= \(\frac{2}{15}\) × \(\frac{30}{1}\)
= 4 students
Hence, from the above,
We can conclude that there are 4 students who play soccer only.
Multiply Fractions Homework & Practice 9.5
Multiply.
\(\frac{1}{4}\) × \(\frac{1}{5}\) = _______
Answer:
\(\frac{1}{4}\) × \(\frac{1}{5}\) = \(\frac{1}{20}\)
Explanation:
The given fractions are: \(\frac{1}{4}\) and \(\frac{1}{5}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{4}\) × \(\frac{1}{5}\)
= \(\frac{1 × 1}{4 × 5}\)
= \(\frac{1}{20}\)
Hence,
\(\frac{1}{4}\) × \(\frac{1}{5}\) = \(\frac{1}{20}\)
Question 2.
\(\frac{2}{7}\) × \(\frac{1}{2}\) = _______
Answer:
\(\frac{1}{2}\) × \(\frac{2}{7}\) = \(\frac{1}{7}\)
Explanation:
The given fractions are: \(\frac{1}{2}\) and \(\frac{2}{7}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{1}{2}\) × \(\frac{2}{7}\)
= \(\frac{1 × 2}{2 × 7}\)
= \(\frac{2}{14}\)
= \(\frac{1}{7}\)
Hence,
\(\frac{1}{2}\) × \(\frac{2}{7}\) = \(\frac{1}{7}\)
Question 3.
\(\frac{9}{10}\) × \(\frac{2}{3}\) = _______
Answer:
\(\frac{9}{10}\) × \(\frac{2}{3}\) = \(\frac{3}{5}\)
Explanation:
The given fractions are: \(\frac{9}{10}\) and \(\frac{2}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{9}{10}\) × \(\frac{2}{3}\)
= \(\frac{9 × 2}{10 × 3}\)
= \(\frac{18}{30}\)
= \(\frac{3}{5}\)
Hence,
\(\frac{9}{10}\) × \(\frac{2}{3}\) = \(\frac{3}{5}\)
Question 4.
\(\frac{5}{8}\) × \(\frac{5}{6}\) = _______
Answer:
\(\frac{5}{8}\) × \(\frac{5}{6}\) = \(\frac{25}{48}\)
Explanation:
The given fractions are: \(\frac{5}{8}\) and \(\frac{5}{6}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{5}{8}\) × \(\frac{5}{6}\)
= \(\frac{5 × 5}{8 × 6}\)
= \(\frac{25}{48}\)
Hence,
\(\frac{5}{8}\) × \(\frac{5}{6}\) = \(\frac{25}{48}\)
Question 5.
\(\frac{9}{7}\) × \(\frac{3}{4}\) = _______
Answer:
\(\frac{9}{7}\) × \(\frac{3}{4}\) = \(\frac{27}{28}\)
Explanation:
The given fractions are: \(\frac{9}{7}\) and \(\frac{3}{4}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{9}{7}\) × \(\frac{3}{4}\)
= \(\frac{9 × 3}{7 × 4}\)
= \(\frac{27}{28}\)
Hence,
\(\frac{9}{7}\) × \(\frac{3}{4}\) = \(\frac{27}{28}\)
Question 6.
\(\frac{11}{100}\) × \(\frac{2}{5}\) = _______
Answer:
\(\frac{11}{100}\) × \(\frac{2}{5}\) = \(\frac{11}{250}\)
Explanation:
The given fractions are: \(\frac{11}{100}\) and \(\frac{2}{5}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{11}{100}\) × \(\frac{2}{5}\)
= \(\frac{11 × 2}{100 × 5}\)
= \(\frac{22}{500}\)
= \(\frac{11}{250}\)
Hence,
\(\frac{11}{100}\) × \(\frac{2}{5}\) = \(\frac{11}{250}\)
Question 7.
\(\frac{7}{20}\) × \(\frac{6}{2}\) = _______
Answer:
\(\frac{7}{20}\) × \(\frac{6}{2}\) = \(\frac{21}{20}\)
Explanation:
The given fractions are: \(\frac{7}{20}\) and \(\frac{6}{2}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{7}{20}\) × \(\frac{6}{2}\)
= \(\frac{7 × 6}{20 × 2}\)
= \(\frac{42}{40}\)
= \(\frac{21}{20}\)
Hence,
\(\frac{7}{20}\) × \(\frac{6}{2}\) = \(\frac{21}{20}\)
Question 8.
\(\frac{15}{16}\) × \(\frac{1}{3}\) = _______
Answer:
\(\frac{15}{16}\) × \(\frac{1}{3}\) = \(\frac{5}{16}\)
Explanation:
The given fractions are: \(\frac{15}{16}\) and \(\frac{1}{3}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{15}{16}\) × \(\frac{1}{3}\)
= \(\frac{15 × 1}{16 × 3}\)
= \(\frac{15}{48}\)
= \(\frac{5}{16}\)
Hence,
\(\frac{15}{16}\) × \(\frac{1}{3}\) = \(\frac{5}{16}\)
Question 9.
\(\frac{5}{12}\) × \(\frac{3}{10}\) = _______
Answer:
\(\frac{5}{12}\) × \(\frac{3}{10}\) = \(\frac{1}{8}\)
Explanation:
The given fractions are: \(\frac{5}{12}\) and \(\frac{3}{10}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
\(\frac{5}{12}\) × \(\frac{3}{10}\)
= \(\frac{5 × 3}{12 × 10}\)
= \(\frac{15}{120}\)
= \(\frac{1}{8}\)
Hence,
\(\frac{5}{12}\) × \(\frac{3}{10}\) = \(\frac{1}{8}\)
Evaluate.
Question 10.
3 × \(\frac{3}{10}\) = _______
Answer:
3 × \(\frac{3}{10}\) = \(\frac{9}{10}\)
Explanation:
The given numbers are: 3 and \(\frac{3}{10}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
3 × \(\frac{3}{10}\)
= \(\frac{3}{1}\) × \(\frac{3}{10}\)
= \(\frac{3 × 3}{10 × 1}\)
= \(\frac{9}{10}\)
Hence,
3 × \(\frac{3}{10}\) = \(\frac{9}{10}\)
Question 11.
\(\left(\frac{1}{3}+\frac{1}{3}\right)\) × \(\frac{4}{5}\) = _______
Answer:
\(\left(\frac{1}{3}+\frac{1}{3}\right)\) × \(\frac{4}{5}\) = \(\frac{8}{15}\)
Explanation:
The given fractions are: \(\frac{1}{3}\), \(\frac{1}{3}\) and \(\frac{4}{5}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
( \(\frac{1}{3}\) + \(\frac{1}{3}\) ) × \(\frac{4}{5}\)
= ( \(\frac{1 + 1}{3}\) ) × \(\frac{4}{5}\)
= \(\frac{2}{3}\) × \(\frac{4}{5}\)
= \(\frac{4 × 2}{3 × 5}\)
= \(\frac{8}{15}\)
Hence,
\(\left(\frac{1}{3}+\frac{1}{3}\right)\) × \(\frac{4}{5}\) = \(\frac{8}{15}\)
Question 12.
\(\frac{6}{7}\) × \(\left(\frac{3}{4}-\frac{5}{12}\right)\) = _______
Answer:
\(\frac{6}{7}\) × \(\left(\frac{3}{4}-\frac{5}{12}\right)\) = \(\frac{2}{7}\)
Explanation:
The given fractions are: \(\frac{6}{7}\), \(\frac{3}{4}\) and \(\frac{5}{12}\)
We know that,
\(\frac{a}{b}\) × \(\frac{p}{q}\)
= \(\frac{a × p}{b × q}\)
a = \(\frac{a}{1}\)
So,
( \(\frac{3}{4}\) – \(\frac{5}{12}\) ) × \(\frac{6}{7}\)
= ( \(\frac{9}{12}\) – \(\frac{5}{12}\) ) × \(\frac{6}{7}\)
= \(\frac{4}{12}\) × \(\frac{6}{7}\)
= \(\frac{4 × 6}{12 × 7}\)
= \(\frac{2}{7}\)
Hence,
\(\frac{6}{7}\) × \(\left(\frac{3}{4}-\frac{5}{12}\right)\) = \(\frac{2}{7}\)
Question 13.
A pancake recipe calls for \(\frac{1}{3}\) cup of water. You want to halve the recipe. What fraction of a cup of water do you need?
Answer:
The fraction of a cup of water you need is: \(\frac{1}{6}\)
Explanation:
It is given that a pancake recipe calls for \(\frac{1}{3}\) cup of water and you want to halve the recipe.
So,
The fraction of a cup of water you need for half of the recipe = ( The cup of water you need for a recipe ) × \(\frac{1}{2}\)
= \(\frac{1}{3}\) × \(\frac{1}{2}\)
= \(\frac{1 × 1}{3 × 2}\)
= \(\frac{1}{6}\)
Hence, from the above,
We can conclude that the fraction of water you need for half of the recipe is: \(\frac{1}{6}\)
Question 14.
Number Sense
Which is greater, \(\frac{3}{4}\) × \(\frac{1}{5}\) or \(\frac{3}{4}\) × \(\frac{1}{8}\)? Explain.
Answer:
\(\frac{3}{4}\) × \(\frac{1}{5}\)” is greater than “\(\frac{3}{4}\) × \(\frac{1}{8}\)
Explanation:
The given fractions are: \(\frac{3}{4}\), \(\frac{1}{5}\) and \(\frac{1}{8}\)
Now,
\(\frac{3}{4}\) × \(\frac{1}{5}\)
= \(\frac{3 × 1}{4 × 5}\)
= \(\frac{3}{20}\)
Now,
\(\frac{3}{4}\) × \(\frac{1}{8}\)
= \(\frac{3 × 1}{4 × 8}\)
= \(\frac{3}{32}\)
So,
For the comparison of the products, equate the numerators.
Multiply \(\frac{3}{20}\) by \(\frac{32}{32}\)
Multiply \(\frac{3}{32}\) by \(\frac{20}{20}\)
So,
\(\frac{3}{20}\) = \(\frac{96}{640}\)
\(\frac{3}{32}\) = \(\frac{60}{640}\)
So,
By comparison of the products,
We can observe that
96 > 60
Hence, from the above,
We can conclude that “\(\frac{3}{4}\) × \(\frac{1}{5}\)” is greater than “\(\frac{3}{4}\) × \(\frac{1}{8}\)”
Question 15.
Reasoning
Is \(\frac{17}{24}\) × \(\frac{7}{8}\) equal to \(\frac{17}{8}\) × \(\frac{7}{24}\)? Explain.
Answer:
\(\frac{17}{24}\) × \(\frac{7}{8}\) is equal to \(\frac{17}{8}\) × \(\frac{7}{24}\)
Explanation:
By the commutative property of multiplication,
a × b = b × a
So,
By the above property of multiplication,
We can interchange the numbers
Hence, from the above,
We can conclude that \(\frac{17}{24}\) × \(\frac{7}{8}\) is equal to \(\frac{17}{8}\) × \(\frac{7}{24}\)
Question 16.
Number Sense
In which equations does k = \(\frac{5}{6}\)?
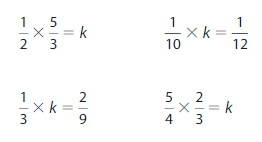
Answer:
Let the multiplication equations be represented A), B), C) and D)
The given expressions are:
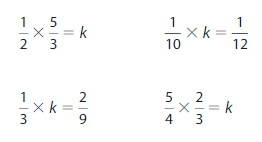
So,
The product of the given expressions are:
A) \(\frac{1}{2}\) × \(\frac{5}{3}\) = \(\frac{5}{6}\)
B) \(\frac{1}{10}\) × k = \(\frac{1}{12}\)
C) \(\frac{1}{3}\) × k = \(\frac{2}{9}\)
D) \(\frac{5}{4}\) × \(\frac{2}{3}\) = k
Hence, from the above expressions,
We can conclude that equation A) fits the value of k perfectly.
Question 17.
Modeling Real Life
At a town hall meeting, \(\frac{37}{50}\) of the members are present. Of those who are present, \(\frac{1}{2}\) vote in favor of a new park. What fraction of the members do not vote in favor of the new park?
Answer:
The fraction of the members that do not vote in favor of the new park is: \(\frac{13}{50}\)
Explanation:
It is given that at a town hall meeting, \(\frac{37}{50}\) of the members are present. Of those who are present, \(\frac{1}{2}\) vote in favor of a new park.
So,
The fraction of the members that do not vote in favor of the new park = ( The total number of members at the town hall meeting ) – ( The fraction of the members that vote in the favor of a new park )
= 1 – \(\frac{37}{50}\)
= \(\frac{50}{50}\) – \(\frac{37}{50}\)
= \(\frac{50 – 37}{50}\)
= \(\frac{13}{50}\)
Hence, from the above,
We can conclude that the number of members that do not vote in the favor of a new park is: \(\frac{13}{50}\)
Question 18.
Modeling Real Life
There are 50 U.S. states. Seven twenty-fifths of the states share a land border with Canada or Mexico.Of those states, \(\frac{2}{7}\) share a border with Mexico. How many states share a border with Canada?
Answer:
The number of states that share a border with Canada is: 4 states
Explanation:
It is given that there are 50 U.S. states. Seven twenty-fifths of the states share a land border with Canada or Mexico and of those states, \(\frac{2}{7}\) share a border with Mexico.
So,
The number of states that share a border with Canada or Mexico = \(\frac{7}{25}\) × 50
= \(\frac{7}{25}\) × \(\frac{50}{1}\)
= 14 states
So,
The number of states that share a border with Canada = \(\frac{2}{7}\) × 14
= \(\frac{2}{7}\) × \(\frac{14}{1}\)
= 4 states
Hence, from the above,
We can conclude that there are 4 states that share a border with Canada
Review & Refresh
Evaluate. Check whether your answer is reasonable.
Question 19.
15.67 + 4 + 6.5 = _____
Answer:
15.67 + 4 + 6.5 = 26.17
Explanation:
The given numbers are: 15.67, 4, and 6.5
The representation of the numbers in the fraction form is: \(\frac{1567}{100}\), \(\frac{65}{10}\) and 4
As the highest number in the denominator is 100, make all the denominators hundred
So,
The representation of 4 with 100 in the denominator is: \(\frac{400}{100}\)
The representation of 6.5 with 100 in the denominator is: \(\frac{650}{100}\)
So,
\(\frac{1567}{100}\) + \(\frac{400}{100}\) + \(\frac{650}{100}\)
= \(\frac{ 1567 + 400 + 650 }{100}\)
= \(\frac{2,617}{100}\)
= 26.17
Hence, 15.67 + 4 + 6.5 = 26.17
Question 20.
20.7 – 9.54 + 25.81 = _______
Answer:
20.7 – 9.54 + 25.81 = 36.97
Explanation:
The given numbers are: 20.7, 9.54, and 25.81
The representation of the numbers in the fraction form is: \(\frac{2581}{100}\), \(\frac{207}{10}\) and \(\frac{954}{100}\)
As the highest number in the denominator is 100, make all the denominators hundred
So,
The representation of 20.7 with 100 in the denominator is: \(\frac{2070}{100}\)
So,
\(\frac{2581}{100}\) + \(\frac{2070}{100}\) – \(\frac{954}{100}\)
= \(\frac{ 2581 + 2070 – 954 }{100}\)
= \(\frac{3,697}{100}\)
= 36.97
Hence, 20.7 – 9.54 + 25.81 = 36.97
Lesson 9.6 Find Areas of Rectangles
Explore and Grow
Draw and cut out a rectangle that has any two of the side lengths below.
\(\frac{1}{2}\) ft
\(\frac{1}{3}\) ft
\(\frac{1}{4}\) ft
Use several copies of your rectangle to create a unit square. What is the area (in square feet) of each small rectangle? Explain your reasoning.
Answer:
Let there are two small rectangles with the following lengths:
\(\frac{1}{2}\) ft and \(\frac{1}{3}\) ft
\(\frac{1}{2}\) ft and \(\frac{1}{4}\) ft
So,
The area of the unit square with lengths \(\frac{1}{2}\) ft and \(\frac{1}{3}\) ft is:
\(\frac{1}{2}\) ft × \(\frac{1}{3}\) ft
= \(\frac{1 × 1}{2 × 3}\) ft
= \(\frac{1}{6}\) ft
The area of the unit square with lengths \(\frac{1}{2}\) ft and \(\frac{1}{4}\) ft is:
\(\frac{1}{2}\) ft × \(\frac{1}{4}\) ft
= \(\frac{1 × 1}{2 × 4}\) ft
= \(\frac{1}{8}\) ft
Hence, from the above,
We can conclude that the areas ofthe smaller rectngles with unit lengths is: \(\frac{1}{6}\) ft and \(\frac{1}{8}\) ft
Reasoning
How can you use a rectangle with unit fraction side lengths to find the area of the rectangle below? Explain your reasoning.
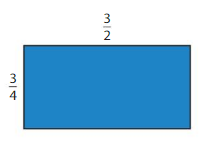
Answer:
The given rectangle is:

To find the area of the rectangle by the unit fractions, multiply the values of the length and the breadth
So,
\(\frac{3}{4}\) × \(\frac{3}{2}\)
= 3 (\(\frac{1}{4}\) ) × 3 ( \(\frac{1}{2}\) )
= 9 ( \(\frac{1}{4}\) × \(\frac{1}{2}\) )
= 9 × \(\frac{1 × 1}{4 × 2}\)
= \(\frac{9}{1}\) × \(\frac{1}{8}\)
= \(\frac{9}{8}\)
The unit fractions are the fractions that contain the value 1 in the numerator.
Here,
\(\frac{1}{4}\) and \(\frac{1}{2}\) are the unit fractions
Think and Grow: Find Areas of Rectangles
One way to find the area of a rectangle with fractional side lengths is to fill it with smaller rectangles.
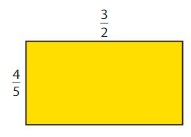
Example
Find the area of the rectangle.
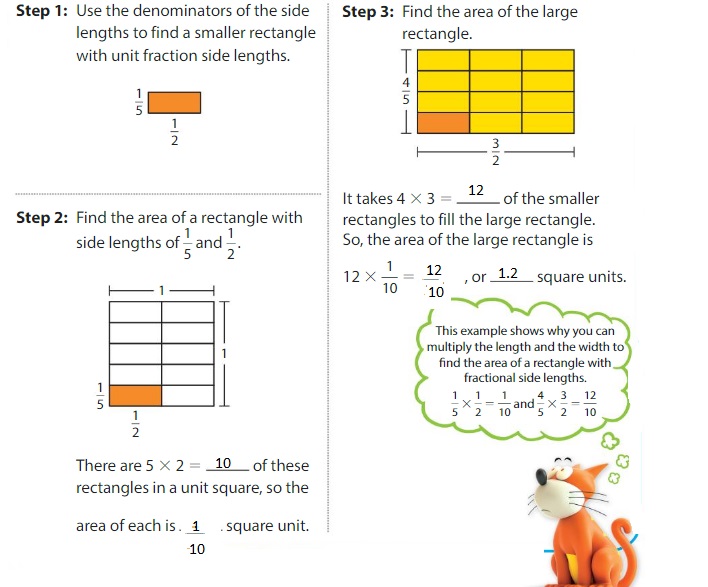
Show and Grow
Question 1.
Find the area of the shaded region.
Answer:
The area of the shaded region is: \(\frac{3}{12}\)
Explanation:
The given figure is:

From the given figure,
The area of the shaded region = \(\frac{3}{4}\) × \(\frac{1}{3}\)
= \(\frac{3 × 1}{4 × 3}\)
= \(\frac{3}{12}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{3}{12}\)
Apply and Grow: Practice
Find the area of the shaded region.
Question 2.
Answer:
The area of the shaded region is: \(\frac{2}{12}\)
Explanation:
The given figure is:

From the given figure,
The area of the shaded region = \(\frac{2}{4}\) × \(\frac{1}{3}\)
= \(\frac{2 × 1}{4 × 3}\)
= \(\frac{2}{12}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{2}{12}\)
Question 3.
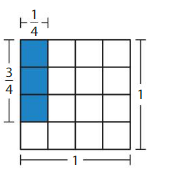
Answer:
The area of the shaded region is: \(\frac{3}{16}\)
Explanation:
The given figure is:

From the given figure,
The area of the shaded region = \(\frac{3}{4}\) × \(\frac{1}{4}\)
= \(\frac{3 × 1}{4 × 4}\)
= \(\frac{3}{16}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{3}{16}\)
Use rectangles with unit fraction side lengths to find the area of the rectangle.
Question 4.

Answer:
The area of the rectangle is: \(\frac{6}{10}\)
Explanation:
The given figure is:

From the given figure,
The area of the rectangle = \(\frac{3}{2}\) × \(\frac{2}{5}\)
= \(\frac{3 × 2}{2 × 5}\)
= \(\frac{6}{10}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{6}{10}\)
Question 5.
Answer:
The area of the rectangle is: \(\frac{10}{18}\)
Explanation:
The given figure is:

From the given figure,
The area of the rectangle = \(\frac{5}{6}\) × \(\frac{2}{3}\)
= \(\frac{5 × 2}{6 × 3}\)
= \(\frac{10}{18}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{10}{18}\)
Question 6.
Find the area of a rectangle with side lengths of \(\frac{5}{8}\) and \(\frac{4}{3}\)?
Answer:
The area of a rectangle is: \(\frac{20}{24}\)
Explanation:
The given side lengths of a rectangle are: \(\frac{5}{8}\) and \(\frac{4}{3}\)
So,
The area of the rectangle = \(\frac{5}{8}\) × \(\frac{4}{3}\)
= \(\frac{5 × 4}{8 × 3}\)
= \(\frac{20}{24}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{20}{24}\)
Question 7.
Find the area of a rectangle with side lengths of \(\frac{7}{9}\) and \(\frac{1}{2}\)?
Answer:
The area of a rectangle is: \(\frac{7}{18}\)
Explanation:
The given side lengths of a rectangle are: \(\frac{7}{9}\) and \(\frac{1}{2}\)
So,
The area of the rectangle = \(\frac{7}{9}\) × \(\frac{1}{2}\)
= \(\frac{7 × 1}{9 × 2}\)
= \(\frac{7}{18}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{7}{18}\)
Question 8.
Reasoning
Can you find the area of a rectangle with fractional side lengths the same way you find the area of a rectangle with whole-number side lengths? Explain.
Answer:
Yes, we can find the area of a rectangle with fractional side lengths the same way you find the area of a rectangle with whole-number side lengths.
Example:
Let the fractional side lengths be: \(\frac{1}{5}\) and \(\frac{1}{9}\)
Let the whole number side lengths be: 3 and 4
So,
The area of the rectangle with the fractional side lengths = \(\frac{1}{5}\) × \(\frac{1}{9}\)
= \(\frac{1 × 1}{9 × 5}\)
= \(\frac{1}{45}\)
The area of the rectangle with the whole number side lengths = 3 × 4
= \(\frac{3}{1}\) × \(\frac{4}{1}\)
= \(\frac{3 × 4}{1 × 1}\)
= \(\frac{12}{1}\)
= 12
Hence, from the above,
We can conclude that we can find the area of a rectangle with fractional side lengths the same way you find the area of a rectangle with whole-number side lengths.
Question 9.
YOU BE THE TEACHER
Our friend says she can find the area of a square given only one fractional side length. Is your friend correct? Explain.
Answer:
Yes, she can find the area of a square by only one fractional side length
Explanation:
Let the unit fractional side length of the square be: \(\frac{1}{2}\)
We know that,
The length of all the sides in a square are equal.
So,
By using this property, we can find the area of the square by taking the fractional unit side length of 1 side as the same for all the sides
So,
The area of the square = \(\frac{1}{2}\) × \(\frac{1}{2}\)
= \(\frac{1 × 1}{2 × 2}\)
= \(\frac{1}{4}\)
Hence, from the above,
We can conclude that she can find the area of a square by only one fractional side length
Think and Grow: Modeling Real Life
Example
A zoo needs an outdoor enclosure with an area of at least \(\frac{3}{10}\) square kilometer10for a camel. Is the rectangular enclosure shown large enough for a camel?
Find the area of the enclosure by multiplying the length and the width.

So, the enclosure is large enough for a camel.
Show and Grow
Question 10.
The area of a square dog kennel is 4 square yards. Will the square mat fit in the kennel?

Answer:
Yes, the square mat will fit in the kennel
Explanation:
It is given that the area of a square dog kennel is 4 square yards and the side of the square mat is \(\frac{5}{3}\) yd
We know that,
The length of all the sides in a square are equal.
So,
By using this property,
The area of the square mat = \(\frac{5}{3}\) × \(\frac{5}{3}\)
= \(\frac{5 × 5}{3 × 3}\)
= \(\frac{25}{9}\) yd
Now,
The area of a square dog kennel can be written as: \(\frac{36}{9}\) yd
So,
When we compare the 2 areas,
We can get 25 < 36
Hence, from the above,
We can conclude that the square mat will fit in the kennel
Question 11.
DIG DEEPER!
The side lengths of each chalk art square are \(\frac{11}{4}\) meters. The side lengths of the square zone around each chalk square are an additional \(\frac{3}{4}\) meter. How many square meters of concrete is used to create the chalk walk shown?

Answer:
The amount of the concrete used to create the chalk walk is: \(\frac{196}{16}\) square meters
Explanation:
It is given that the side lengths of each chalk art square are \(\frac{11}{4}\) meters. The side lengths of the square zone around each chalk square are an additional \(\frac{3}{4}\) meter.
So,
The total side length of the chalk walk = \(\frac{11}{4}\) + \(\frac{3}{4}\)
= \(\frac{11 + 3}{4}\)
= \(\frac{14}{4}\) meters
We know that,
The length of all sides in the square are equal.
So,
By using this property,
The amount of concrete used for the chalk walk = \(\frac{14}{4}\) × \(\frac{14}{4}\)
= \(\frac{14 × 14}{4 × 4}\)
= \(\frac{196}{16}\) square meters
Hence, from the above,
We can conclude that the amount of the concrete used to create the chalk walk is: \(\frac{196}{16}\) square meters
Find Areas of Rectangles Homework & Practice 9.6
Find the area of the shaded region.
Question 1.
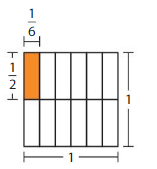
Answer:
The area of the shaded region is: \(\frac{1}{12}\)
Explanation:
The given figure is:

From the given figure,
The area of the shaded region = \(\frac{1}{2}\) × \(\frac{1}{6}\)
= \(\frac{1 × 1}{2 × 6}\)
= \(\frac{1}{12}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{1}{12}\)
Question 2.
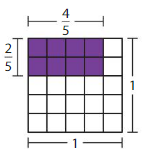
Answer:
The area of the shaded region is: \(\frac{8}{25}\)
Explanation:
The given figure is:

From the given figure,
The area of the shaded region = \(\frac{2}{5}\) × \(\frac{4}{5}\)
= \(\frac{2 × 4}{5 × 5}\)
= \(\frac{8}{25}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{8}{25}\)
Use rectangles with unit fraction side lengths to find the area of the rectangle.
Question 3.
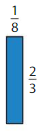
Answer:
The area of the rectangle is: \(\frac{2}{24}\)
Explanation:
The given figure is:

From the given figure,
The area of the rectangle = \(\frac{2}{3}\) × \(\frac{1}{8}\)
= \(\frac{1 × 2}{3 × 8}\)
= \(\frac{2}{24}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{2}{24}\)
Question 4.
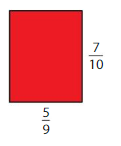
Answer:
The area of the rectangle is: \(\frac{35}{90}\)
Explanation:
The given figure is:

From the given figure,
The area of the rectangle = \(\frac{7}{10}\) × \(\frac{5}{9}\)
= \(\frac{7 × 5}{10 × 9}\)
= \(\frac{35}{90}\)
Hence, from the above,
We can conclude that the area of the shaded region is: \(\frac{35}{90}\)
Question 5.
Find the area of a rectangle with a side length of \(\frac{3}{4}\) and \(\frac{5}{12}\).
Answer:
The area of a rectangle is: \(\frac{15}{48}\)
Explanation:
The given side lengths of a rectangle are: \(\frac{5}{12}\) and \(\frac{3}{4}\)
So,
The area of the rectangle = \(\frac{5}{12}\) × \(\frac{3}{4}\)
= \(\frac{5 × 3}{12 × 4}\)
= \(\frac{15}{48}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{15}{48}\)
Question 6.
Find the area of a square with side lengths of \(\frac{9}{16}\)
Answer:
The area of a square is: \(\frac{81}{256}\)
Explanation:
We know that,
The length of all the sides of the square is equal.
So,
The given side lengths of a square are: \(\frac{9}{16}\) and \(\frac{9}{16}\)
So,
The area of the square = \(\frac{9}{16}\) × \(\frac{9}{16}\)
= \(\frac{9 × 9}{16 × 16}\)
= \(\frac{81}{256}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{81}{256}\)
Question 7.
Open-Ended
The area of a rectangle is \(\frac{16}{24}\). What are the possible side lengths of the rectangle?
Answer:
The possible side lengths for the given area of a rectangle are:
A) \(\frac{4}{2}\) and \(\frac{4}{12}\)
B) \(\frac{1}{3}\) and \(\frac{4}{8}\)
Explanation:
The given area of a rectangle is: \(\frac{16}{24}\)
So,
To find the possible side lengths of a rectangle, find the factors for the numerator and denominator of \(\frac{16}{24}\)
So,
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
So,
The possible side lengths of a rectangle are:
A) \(\frac{4}{2}\) and \(\frac{4}{12}\)
B) \(\frac{1}{3}\) and \(\frac{4}{8}\)
There are so many possible side lengths of a rectangle like above
Hence, from the above,
We can conclude that the possible side lengths of a rectangle are:
A) \(\frac{4}{2}\) and \(\frac{4}{12}\)
B) \(\frac{1}{3}\) and \(\frac{4}{8}\)
Question 8.
Structure
Write an expression that represents the area of the shaded rectangle.
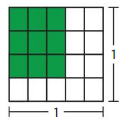
Answer:
The expression that represents the area of the shaded region is: \(\frac{1}{3}\) × \(\frac{1}{3}\)
Explanation:
The given shaded rectangle is:

From the given shaded rectangle,
The number of shaded columns is: 3
The number of shaded rows is: 3
The total number of rows is: 1
The total number of columns are: 1
So,
The expression representing the shaded region = \(\frac{The total number of rows}{The number of shaded rows}\) × \(\frac{The total number of rows}{The number of shaded rows}\)
= \(\frac{1}{3}\) × \(\frac{1}{3}\)
Hence, from the above,
We can conclude that the expression representing the shaded region of a rectangle is: \(\frac{1}{3}\) × \(\frac{1}{3}\)
Question 9.
Modeling Real Life
The area of a square table is 9 square feet. Will the board game fit on the table?

Answer:
Yes, the board game fit on the table
Explanation:
The given area of a square table is 9 square feet
So,
The representation of the area of the square table in the fraction form is: \(\frac{36}{4}\)
Now,
The given board game is:

The area of the board game can find out by multiplying its side lengths
So,
The area of the board game = \(\frac{3}{2}\) × \(\frac{5}{2}\)
= \(\frac{3 × 5}{2 × 2}\)
= \(\frac{15}{4}\)
So,
Compare the area of the square table and the area of the board game,
We get
Area of the square table > Area of the board game
Hence, from the above,
We can conclude that the board game fit on the table
Review & Refresh
Divide. Then check your answer.
Question 10.
365 ÷ 14 = _______
Answer:
365 ÷ 14 = 26 R 1
Explanation:
By using the partial quotients method,
365 ÷ 14 = ( 280 ÷ 84 ) ÷ 14
= ( 280 ÷ 14 ) + ( 84 ÷ 14 )
= 20 + 6
= 26 R 1
Hence, 365 ÷ 14 = 26 R 1
Question 11.
282 ÷ 27 = ______
Answer:
282 ÷ 27 = 10 R 12
Explanation:
By using the partial quotients method,
282 ÷ 27 = 270 ÷ 27
= 10 R 12
Hence, 270 ÷ 27 = 10 R 12
Question 12.
601 ÷ 72 = _____
Answer:
601 ÷ 72 = 8 R 25
Explanation:
By using the partial quotients method,
601 ÷ 72 = 576 ÷ 72
= 8 R 25
Hence, 601 ÷ 72 = 8 R 25
Lesson 9.7 Multiply Mixed Numbers
Explore and Grow
Find the area of the rectangle. Explain how you found your answer.
Answer:
The area of the rectangle is: \(\frac{35}{4}\)
Explanation:
The given rectangle is:
From the above rectangle,
The side lengths are: 2\(\frac{1}{2}\) and 3\(\frac{1}{2}\)
The representation of the side lengths in the improper form is: \(\frac{5}{2}\) and \(\frac{7}{2}\)
So,
The area of rectangle = \(\frac{5}{2}\) × \(\frac{7}{2}\)
= \(\frac{5 × 7}{2 × 2}\)
= \(\frac{35}{4}\)
Hence,
2\(\frac{1}{2}\) × 3\(\frac{1}{2}\) = \(\frac{35}{4}\)
Structure
Find the area using a different method. Explain how you found your answer.
Answer:
The given mixed fractions of a rectangle are: 2\(\frac{1}{2}\) and 3\(\frac{1}{2}\)
To convert a mixed fraction into an improper fraction, we have to add the whole number part and the fractional part in the mixed fraction.
So,
2\(\frac{1}{2}\) = 2 + \(\frac{1}{2}\)
= \(\frac{4}{2}\) + \(\frac{1}{2}\)
= \(\frac{5}{2}\)
3\(\frac{1}{2}\) = 3 + \(\frac{1}{2}\)
= \(\frac{6}{2}\) + \(\frac{1}{2}\)
= \(\frac{7}{2}\)
So,
\(\frac{5}{2}\) × \(\frac{7}{2}\) = \(\frac{35}{4}\)
Think and Grow: Multiply Mixed Numbers
You can use a model to find the product of two mixed numbers. You can also write the mixed numbers as improper fractions and then multiply.
Example
Find 1\(\frac{1}{2}\) × 2\(\frac{3}{4}\).
One Way: Use an area model.
Step 1: Write each mixed number as a sum.
1\(\frac{1}{2}\) = 1 + \(\frac{1}{2}\) 2\(\frac{3}{4}\) = 2 + \(\frac{3}{4}\)
Step 2: Draw an area model that represents the product of the sums.
Step 3: Find the sum of the areas of the sections.
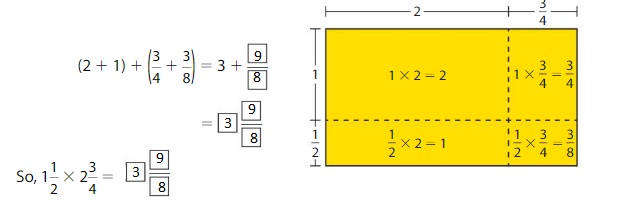
Another Way: Write each mixed number as an improper fraction, then multiply.

Show and Grow
Multiply.
Question 1.
2\(\frac{1}{2}\) × 1\(\frac{1}{2}\) = ________
Answer:
2\(\frac{1}{2}\) × 1\(\frac{1}{2}\) = \(\frac{15}{4}\)
Explanation:
The given fractions are: 2\(\frac{1}{2}\) and 1\(\frac{1}{2}\)
The representation of the fractions in the improper form is: \(\frac{5}{2}\) and \(\frac{3}{2}\)
So,
\(\frac{5}{2}\) × \(\frac{3}{2}\)
= \(\frac{5 × 3}{2 × 2}\)
= \(\frac{15}{4}\)
Hence,
2\(\frac{1}{2}\) × 1\(\frac{1}{2}\) = \(\frac{15}{4}\)
Question 2.
3\(\frac{1}{4}\) × 2\(\frac{2}{3}\) = ______
Answer:
3\(\frac{1}{4}\) × 2\(\frac{2}{3}\) = \(\frac{104}{12}\)
Explanation:
The given fractions are: 3\(\frac{1}{4}\) and 2\(\frac{2}{3}\)
The representation of the fractions in the improper form is: \(\frac{13}{4}\) and \(\frac{8}{3}\)
So,
\(\frac{13}{4}\) × \(\frac{8}{3}\)
= \(\frac{13 × 8}{4 × 3}\)
= \(\frac{104}{12}\)
Hence,
3\(\frac{1}{4}\) × 2\(\frac{2}{3}\) = \(\frac{104}{12}\)
Apply and Grow: Practice
Multiply.
Question 3.
1\(\frac{3}{4}\) × 2\(\frac{1}{6}\) = ______
Answer:
1\(\frac{3}{4}\) × 2\(\frac{1}{6}\) = \(\frac{91}{24}\)
Explanation:
The given fractions are: 1\(\frac{3}{4}\) and 2\(\frac{1}{6}\)
The representation of the fractions in the improper form is: \(\frac{7}{4}\) and \(\frac{13}{6}\)
So,
\(\frac{7}{4}\) × \(\frac{13}{6}\)
= \(\frac{13 × 7}{4 × 6}\)
= \(\frac{91}{24}\)
Hence,
1\(\frac{3}{4}\) × 2\(\frac{1}{6}\) = \(\frac{91}{24}\)
Question 4.
4\(\frac{1}{3}\) × 1\(\frac{5}{6}\) = ______
Answer:
4\(\frac{1}{3}\) × 1\(\frac{5}{6}\) = \(\frac{143}{18}\)
Explanation:
The given fractions are: 4\(\frac{1}{3}\) and 1\(\frac{5}{6}\)
The representation of the fractions in the improper form is: \(\frac{13}{3}\) and \(\frac{11}{6}\)
So,
\(\frac{13}{3}\) × \(\frac{11}{6}\)
= \(\frac{13 × 11}{6 × 3}\)
= \(\frac{143}{18}\)
Hence,
4\(\frac{1}{3}\) × 1\(\frac{5}{6}\) = \(\frac{143}{18}\)
Question 5.
3\(\frac{2}{5}\) × 1\(\frac{9}{10}\) = ______
Answer:
3\(\frac{2}{5}\) × 1\(\frac{9}{10}\) = \(\frac{323}{50}\)
Explanation:
The given fractions are: 3\(\frac{2}{5}\) and 1\(\frac{9}{10}\)
The representation of the fractions in the improper form is: \(\frac{17}{5}\) and \(\frac{19}{10}\)
So,
\(\frac{17}{5}\) × \(\frac{19}{10}\)
= \(\frac{17 × 19}{5 × 10}\)
= \(\frac{323}{50}\)
Hence,
3\(\frac{2}{5}\) × 1\(\frac{9}{10}\) = \(\frac{323}{50}\)
Question 6.
2\(\frac{3}{8}\) × 3\(\frac{1}{2}\) = ______
Answer:
2\(\frac{3}{8}\) × 3\(\frac{1}{2}\) = \(\frac{133}{16}\)
Explanation:
The given fractions are: 2\(\frac{3}{8}\) and 3\(\frac{1}{2}\)
The representation of the fractions in the improper form is: \(\frac{19}{8}\) and \(\frac{7}{2}\)
So,
\(\frac{19}{8}\) × \(\frac{7}{2}\)
= \(\frac{19 × 7}{8 × 2}\)
= \(\frac{133}{16}\)
Hence,
2\(\frac{3}{8}\) × 3\(\frac{1}{2}\) = \(\frac{133}{16}\)
Evaluate.
Question 7.
5\(\frac{1}{4}\) × \(\frac{2}{5}\) × 6\(\frac{1}{12}\) = _________
Answer:
5\(\frac{1}{4}\) × \(\frac{2}{5}\) × 6\(\frac{1}{12}\) = \(\frac{3,066}{240}\)
Explanation:
The given fractions are: 5\(\frac{1}{4}\), \(\frac{2}{5}\) and 6\(\frac{1}{12}\)
The representation of the fractions in the improper form is: \(\frac{21}{4}\) and \(\frac{73}{12}\)
So,
\(\frac{21}{4}\) × \(\frac{73}{12}\) × \(\frac{2}{5}\)
= \(\frac{21 × 73 × 2}{4 × 12 × 5}\)
= \(\frac{3,066}{240}\)
Hence,
5\(\frac{1}{4}\) × \(\frac{2}{5}\) × 6\(\frac{1}{12}\) = \(\frac{3,066}{240}\)
Question 8.
3\(\frac{2}{3}\) × (10\(\frac{7}{8}\) – 2\(\frac{1}{4}\)) = _________
Answer:
3\(\frac{2}{3}\) × (10\(\frac{7}{8}\) – 2\(\frac{1}{4}\)) = \(\frac{759}{24}\)
Explanation:
The given fractions are: 3\(\frac{2}{3}\), 10\(\frac{7}{8}\) and 2\(\frac{1}{4}\)
The representation of the fractions in the improper form is: \(\frac{11}{3}\), \(\frac{87}{8}\) and \(\frac{9}{4}\)
So,
3\(\frac{2}{3}\) × (10\(\frac{7}{8}\) – 2\(\frac{1}{4}\))
= \(\frac{11}{3}\) × ( \(\frac{87}{8}\) – \(\frac{9}{4}\) )
= \(\frac{11}{3}\) × ( \(\frac{87 – 18}{8}\) )
= \(\frac{11}{3}\) × \(\frac{69}{8}\)
= \(\frac{11 × 69}{8 × 3}\)
= \(\frac{759}{24}\)
Hence,
3\(\frac{2}{3}\) × (10\(\frac{7}{8}\) – 2\(\frac{1}{4}\)) = \(\frac{759}{24}\)
Question 9.
YOU BE THE TEACHER
Your friend uses the model to find 4\(\frac{1}{2}\) × 3\(\frac{2}{3}\). Is your friend correct? Explain.
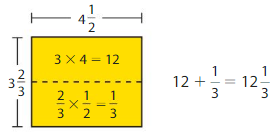
Answer:
No, your friend is not correct
Explanation:
The given fractions are: 4\(\frac{1}{2}\) and 3\(\frac{2}{3}\)
The representation of the side lengths in the improper form is: \(\frac{9}{2}\) and \(\frac{11}{3}\)
So,
The area of rectangle = \(\frac{9}{2}\) × \(\frac{11}{3}\)
= \(\frac{9 × 11}{3 × 2}\)
= \(\frac{99}{6}\)
= \(\frac{33}{2}\)
= 15\(\frac{3}{2}\)
But according to your friend,
4\(\frac{1}{2}\) × 3\(\frac{2}{3}\) = 12\(\frac{1}{2}\)
Hence, from the above,
We can conclude that your friend is not correct.
Question 10.
Logic
Find the missing numbers.
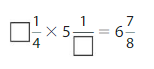
Answer:
The missing numbers are: 1 and \(\frac{8}{5}\)
Explanation:
According to the separation method,
To convert the mixed number into the improper fraction, we can add whole numbers and the fractions separately
Now,
Let the missing numbers be p and q
So,
p + 5 = 6
So,
p = 6 – 5 = 1
Now,
\(\frac{1}{4}\) + \(\frac{1}{q}\) = \(\frac{7}{8}\)
So,
\(\frac{1}{q}\) = \(\frac{7}{8}\) – \(\frac{1}{4}\)
= \(\frac{7}{8}\) – \(\frac{2}{8}\)
= \(\frac{7 – 2}{8}\)
= \(\frac{5}{8}\)
So,
q= \(\frac{8}{5}\)
Hence, from the above,
We can conclude that the missing numbers are: 1 and \(\frac{8}{5}\)
Think and Grow: Modeling Real Life
Example
A construction crew is paving 15 miles of a highway. The crew paves 4\(\frac{2}{10}\) miles each month. Does the crew finish paving the highway in 3\(\frac{1}{2}\) months?

Find the length of the highway the crew paves by multiplying the number of months by the number of miles they pave each month. Write each mixed number as an improper fraction, then multiply.

Compare the length the crew paves to the amount that needs to be paved.
The Crew can finish paving the highway in 3\(\frac{1}{2}\) months.
Show and Grow
Question 11.
You have 3 cups of strawberries. You want to make 1\(\frac{1}{2}\) batches of the recipe. Do you have enough strawberries?

Answer:
Yes, you have enough strawberries
Explanation:
The given recipe for a strawberry smoothie is:

It is given that you want to make 1\(\frac{1}{2}\) batches of the recipe
From the table,
The number of cups of strawberry is: 1\(\frac{3}{4}\)
Now,
The representation of 1\(\frac{1}{2}\) in the iproper fraction is: \(\frac{3}{2}\)
The representation of 1\(\frac{3}{4}\) in the mixed form is: \(\frac{7}{4}\)
So,
The number of strawberries for the recipe = \(\frac{3}{2}\) × \(\frac{7}{4}\)
= \(\frac{3 × 7}{4 × 2}\)
= \(\frac{21}{8}\)
It is also given that you have 3 cups of strawberries
So,
We can write 3 in the fraction form and as the multiples of 8 is: \(\frac{24}{8}\)
So,
When we compare the number of cups we obtained and given,
We can say that we have enough strawberries to make the recipe
Hence, from the above,
We can conclude that we have enough strawberries
Question 12.
On Monday,you roller-skate 6\(\frac{1}{4}\) miles. On Tuesday, you skate 1\(\frac{2}{5}\) times as far as you did on Monday. How many total miles do you roller-skate on Monday and Tuesday combined?
Answer:
The number of miles you do roller-skate on Monday and Tuesday combined is: 15 miles
Explanation:
It is given that on Monday,you roller-skate 6\(\frac{1}{4}\) miles. On Tuesday, you skate 1\(\frac{2}{5}\) times as far as you did on Monday.
So,
The number of miles you do roller-skate on Tuesday = ( The number of miles you do roller-skate on Monday ) × 1\(\frac{2}{5}\)
= 6\(\frac{1}{4}\) × 1\(\frac{2}{5}\)
= \(\frac{25}{4}\) × \(\frac{7}{5}\)
= \(\frac{25 × 7}{5 × 4}\)
= \(\frac{175}{20}\)
Now,
The number of miles you do roller-skate on Monday and Tuesday combined = 6\(\frac{1}{4}\) + \(\frac{175}{20}\)
= \(\frac{25}{4}\) + \(\frac{175}{20}\)
= \(\frac{125}{20}\) + \(\frac{175}{20}\)
= \(\frac{175 + 125}{20}\)
= \(\frac{300}{20}\)
= 15 miles
Hence, from the above,
We can conclude that the number of miles you do roller- skate on Monday and Tuesday combined is: 15 miles
Question 13.
DIG DEEPER!
An artist paints a rectangular mural. The mural is 4\(\frac{1}{3}\) feet wide. The length is 2\(\frac{1}{4}\) times the width. What is the area of the mural?
Answer:
The area of the mural is: \(\frac{117}{12}\) square feet
Explanation:
It is given that an artist paints a rectangular mural. The mural is 4\(\frac{1}{3}\) feet wide. The length is 2\(\frac{1}{4}\) times the width.
So,
The area of the mural = ( The width of the mural ) × ( The length of the mural )
= 4\(\frac{1}{3}\) × 2\(\frac{1}{4}\)
= \(\frac{13}{3}\) × \(\frac{9}{4}\)
= \(\frac{13 × 9}{4 × 3}\)
= \(\frac{117}{12}\)
Hence, from the above,
We can conclude that the area of the mural is: \(\frac{117}{12}\) square feet
Multiply Mixed Numbers Homework & Practice 9.7
Multiply.
Question 1.
1\(\frac{1}{2}\) × 1\(\frac{1}{8}\) = ______
Answer:
1\(\frac{1}{2}\) × 1\(\frac{1}{8}\) = \(\frac{18}{16}\)
Explanation:
The given fractions are: 1\(\frac{1}{2}\) and 1\(\frac{1}{8}\)
The representation of the fractions in the improper form is: \(\frac{3}{2}\) and \(\frac{9}{8}\)
So,
\(\frac{9}{8}\) × \(\frac{3}{2}\)
= \(\frac{9 × 3}{8 × 2}\)
= \(\frac{18}{16}\)
Hence,
1\(\frac{1}{2}\) × 1\(\frac{1}{8}\) = \(\frac{18}{16}\)
Question 2.
1\(\frac{5}{6}\) × 2\(\frac{1}{4}\) = ______
Answer:
1\(\frac{5}{6}\) × 2\(\frac{1}{4}\) = \(\frac{99}{24}\)
Explanation:
The given fractions are: 1\(\frac{5}{6}\) and 2\(\frac{1}{4}\)
The representation of the fractions in the improper form is: \(\frac{11}{6}\) and \(\frac{9}{4}\)
So,
\(\frac{9}{4}\) × \(\frac{11}{6}\)
= \(\frac{9 × 11}{4 × 6}\)
= \(\frac{99}{24}\)
Hence,
1\(\frac{5}{6}\) × 2\(\frac{1}{4}\) = \(\frac{99}{24}\)
Evaluate.
Question 3.
2\(\frac{3}{8}\) × 2\(\frac{3}{4}\) = ______
Answer:
2\(\frac{3}{8}\) × 2\(\frac{3}{4}\) = \(\frac{209}{32}\)
Explanation:
The given fractions are: 2\(\frac{3}{8}\) and 2\(\frac{3}{4}\)
The representation of the fractions in the improper form is: \(\frac{19}{8}\) and \(\frac{11}{4}\)
So,
\(\frac{19}{8}\) × \(\frac{11}{4}\)
= \(\frac{19 × 11}{4 × 8}\)
= \(\frac{209}{32}\)
Hence,
2\(\frac{3}{8}\) × 2\(\frac{3}{4}\) = \(\frac{209}{32}\)
Question 4.
4\(\frac{1}{6}\) × 3\(\frac{2}{7}\) = ______
Answer:
4\(\frac{1}{6}\) × 3\(\frac{2}{7}\) = \(\frac{575}{42}\)
Explanation:
The given fractions are: 4\(\frac{1}{6}\) and 3\(\frac{2}{7}\)
The representation of the fractions in the improper form is: \(\frac{25}{6}\) and \(\frac{23}{7}\)
So,
\(\frac{23}{7}\) × \(\frac{25}{6}\)
= \(\frac{23 × 25}{7 × 6}\)
= \(\frac{575}{42}\)
Hence,
4\(\frac{1}{6}\) × 3\(\frac{2}{7}\) = \(\frac{575}{42}\)
Question 5.
2\(\frac{1}{3}\) × 3\(\frac{9}{10}\) × 5\(\frac{1}{5}\) = ______
Answer:
2\(\frac{1}{3}\)× 3\(\frac{9}{10}\) ×5\(\frac{1}{5}\) = \(\frac{7,098}{150}\)
Explanation:
The given fractions are: 2\(\frac{1}{3}\), 3\(\frac{9}{10}\) and 5\(\frac{1}{5}\)
The representation of the fractions in the improper form is: \(\frac{7}{3}\), \(\frac{39}{10}\) and \(\frac{26}{5}\)
So,
\(\frac{7}{3}\) × \(\frac{39}{10}\) ×\(\frac{26}{5}\)
= \(\frac{7 × 39 × 26}{3 × 10 × 5}\)
= \(\frac{7,098}{150}\)
Hence,
2\(\frac{1}{3}\)× 3\(\frac{9}{10}\) ×5\(\frac{1}{5}\) = \(\frac{7,098}{150}\)
Question 6.
(1\(\frac{7}{8}\) + 4\(\frac{4}{5}\)) × 2\(\frac{1}{12}\) = _______
Answer:
(1\(\frac{7}{8}\) + 4\(\frac{4}{5}\)) × 2\(\frac{1}{12}\) = \(\frac{6,675}{480}\)
Explanation:
The given fractions are: 1\(\frac{7}{8}\), 4\(\frac{4}{5}\) and 2\(\frac{1}{12}\)
The representation of the fractions in the improper form is: \(\frac{15}{8}\), \(\frac{24}{5}\) and \(\frac{25}{12}\)
So,
(1\(\frac{7}{8}\) + 4\(\frac{4}{5}\)) × \(\frac{25}{12}\)
= ( \(\frac{15}{8}\) + \(\frac{24}{5}\) ) × \(\frac{25}{12}\)
= ( \(\frac{75}{40}\) + \(\frac{192}{40}\) ) × \(\frac{25}{12}\)
= \(\frac{75 + 192}{40}\) × \(\frac{25}{12}\)
= \(\frac{267}{40}\) × \(\frac{25}{12}\)
= \(\frac{267 × 25}{40× 12 }\)
= \(\frac{6,675}{480}\)
Hence,
(1\(\frac{7}{8}\) + 4\(\frac{4}{5}\)) × 2\(\frac{1}{12}\) = \(\frac{6,675}{480}\)
Question 7.
Structure
Find the missing numbers.
Answer:
The missing numbers are: 5 and \(\frac{3}{10}\)
Explanation:
Let the missing numbers be p and q
By using the partial products method,
( p × 4 ) + ( p × \(\frac{1}{7}\) ) = 20 + \(\frac{5}{7}\)
p × ( 4 + \(\frac{1}{7}\) ) = 20 + \(\frac{5}{7}\)
p × \(\frac{29}{7}\) = \(\frac{145}{7}\)
So,
p = \(\frac{145}{7}\) ÷ \(\frac{29}{7}\)
= \(\frac{145}{7}\) × \(\frac{7}{29}\)
= \(\frac{145 × 7}{7 × 29}\)
= 5
Now,
(q × 4 ) + ( q × \(\frac{1}{7}\) ) = \(\frac{12}{10}\) + \(\frac{3}{70}\)
q × ( 4 + \(\frac{1}{7}\) ) = \(\frac{12}{10}\) + \(\frac{3}{70}\)
q × \(\frac{29}{7}\) = \(\frac{84 + 3}{70}\)
q × \(\frac{29}{7}\) = \(\frac{87}{70}\)
So,
q = \(\frac{87}{70}\) ÷ \(\frac{29}{7}\)
= \(\frac{87}{70}\) × \(\frac{7}{29}\)
= \(\frac{87 × 7}{70 × 29}\)
= \(\frac{3}{10}\)
Hence, from the above,
We can conclude that the missing numbers are: 5 and \(\frac{3}{10}\)
Question 8.
YOU BE THE TEACHER
Your friend finds 1\(\frac{11}{12}\) × 2\(\frac{3}{8}\) . Is your friend correct? Explain.
Answer:
Yes your friend is correct
Explanation:
The given mixed numbers are: 1\(\frac{11}{12}\) and 2\(\frac{3}{8}\)
The representation of the mixed numbers in the fraction form is: \(\frac{23}{12}\) and \(\frac{19}{8}\)
So,
\(\frac{23}{12}\) × \(\frac{19}{8}\)
= \(\frac{23 × 19}{8 × 12}\)
= \(\frac{437}{96}\)
= 4\(\frac{53}{96}\)
Hence, from the above,
We can conclude that your friend is correct
Question 9.
Modeling Real Life
Your friend earns 7\(\frac{1}{2}\) dollars each hour. Will she earn enough money to buy a $35 toy after working 4\(\frac{3}{4}\) hours?
Answer:
she can’t earn enough money to buy $35 toy after working 4\(\frac{3}{4}\) hours
Explanation:
It is given that your friend earns 7\(\frac{1}{2}\) dollars each hour.
It is given that will she earn enough money to buy a $35 toy after working 4\(\frac{3}{4}\) hours
So,
The number of dollars she can earn = 7\(\frac{1}{2}\) × 4\(\frac{3}{4}\)
= \(\frac{15}{2}\) × \(\frac{19}{4}\)
= \(\frac{15 × 19}{4 × 2}\)
= \(\frac{285}{8}\)
Now,
The representation of $35 as the multiple of 8 is: \(\frac{280}{8}\)
So,
By comparing the given money with he money she earned,
We can say that she can’t buy the toy.
Hence, from the above,
We can conclude that she can’t earn enough money to buy a $35 toy after working 4\(\frac{3}{4}\) hours
Question 10.
Modeling Real Life
One class collects 8\(\frac{1}{4}\) pounds of recyclable materials. Another class collects 1\(\frac{1}{2}\) times as many pounds as the first class. How many pounds of recyclable materials do the two classes collect altogether?
Answer:
The number of pounds of recyclable materials the two classes collects together is: \(\frac{231}{8}\) pounds
Explanation:
It is given that one class collects 8\(\frac{1}{4}\) pounds of recyclable materials. Another class collects 1\(\frac{1}{2}\) times as many pounds as the first class.
So,
The number of pounds of recyclable materials collected by another class = 8\(\frac{1}{4}\) × 1\(\frac{1}{2}\)
= \(\frac{33}{4}\) × \(\frac{3}{2}\)
= \(\frac{99}{8}\) pounds
So,
The number of pouds of recyclable materials collected by two classes together = 8\(\frac{1}{4}\) + \(\frac{99}{8}\)
= \(\frac{33}{4}\) + \(\frac{99}{8}\)
= \(\frac{132 + 99}{8}\)
= \(\frac{231}{8}\) pounds
Hence, from the above,
We can conclude that the number of pounds of recyclable materials the two classes collects together is: \(\frac{231}{8}\) pounds
Review & Refresh
Find the product.
Question 11.
6 × 5.7 = ______
Answer:
6 × 5.7 = 34.2
Explanation:
By using the partial products method,
6 × 5.7 = 6 × ( 5 + 0.7 )
= ( 6 × 5 ) + ( 6 × 0.7 )
= 30 + 4.2
= 34.2
Hence, 6 × 5.7 = 34.2
Question 12.
0.84 × 9 = ______
Answer:
0.84 × 9 = 73.17
Explanation:
By using the partial quotients method,
0.84 × 9 = ( 0.81 + 0.03 ) × 9
= ( 0.81 × 9 ) + ( 0.03 × 9 )
= 72.9 + 0.27
= 73.17
Hence, 0.84 × 9 = 73.17
Lesson 9.8 Compare Factors and Products
Explore and Grow
Without calculating, order the rectangles by area from least to greatest. Explain your reasoning.
Answer:
Let the given rectangles be named A), B), C), and D)
So,
The side lengths of A are: 1 and 1\(\frac{1}{2}\)
The side lengths of B are: 1\(\frac{1}{3}\) and \(\frac{11}{12}\)
The side lengths of C are: \(\frac{3}{2}\) and \(\frac{11}{12}\)
The side lengths of D are: \(\frac{11}{10}\) and \(\frac{3}{2}\)
Now,
The area of A is: \(\frac{1}{2}\)
The area of B is: \(\frac{44}{36}\)
The area of C is: \(\frac{33}{24}\)
The area of D is: \(\frac{33}{20}\)
For comparison make the denominators of the areas of the four rectangles equal.
So,
The area of A is: \(\frac{18}{36}\)
The area of B is: \(\frac{44}{36}\)
So, by comparing these 2 areas,
We can say that B is greater
Now,
The area of C is: \(\frac{165}{120}\)
The area of D is: \(\frac{198}{120}\)
So, by comparing these 2 areas,
We can say that D is greater
Hence, from the above,
We can conclude that the order of rectangles by areas from the greatest to the least is: B > D> A > C
Construct Arguments
Explain your strategy to your partner. Compare your strategies.
Answer:
The strategy you followed is:
A) Write the side lengths of the rectangles
B) Find the areas of the four rectangles
C) Make the denominators of all the four areas of rectangles equal
D) Compare the numerators of all the four areas of the four rectangles
Think and Grow: Compare Factors and Products
Key Idea
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
Example
Without calculating, tell whether the product 3\(\frac{1}{8}\) × \(\frac{5}{6}\) is less than, greater than, or equal to or each of its factors.

Show and Grow
Without calculating, tell whether the product is less than, greater than, or equal to each of its factors.
Question 1.
8 × \(\frac{3}{10}\)
Answer:
The value of 8 × \(\frac{3}{10}\) is less than 8
Explanation:
The given numbers are: 8 and \(\frac{3}{10}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{3}{10}\) is less than 1
So,
8 × \(\frac{3}{10}\) is less than 8
Hence, from the above,
We can conclude that the value of 8 × \(\frac{3}{10}\) is less than 8
Question 2.
\(\frac{4}{4}\) × 5\(\frac{2}{3}\)
Answer:
The value of \(\frac{4}{4}\) × 5\(\frac{2}{3}\) is greater than \(\frac{4}{4}\)
Explanation:
The given fractions are: \(\frac{4}{4}\) and 5\(\frac{2}{3}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
We know that,
\(\frac{4}{4}\) is 1
Now,
The representation of 5\(\frac{2}{3}\) in the improper fraction form is: \(\frac{17}{3}\)
So,
\(\frac{17}{3}\) is greater than 1
So,
\(\frac{4}{4}\) × 5\(\frac{2}{3}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{4}{4}\) × 5\(\frac{2}{3}\) is greater than \(\frac{4}{4}\)
Question 3.
\(\frac{4}{3}\) × \(\frac{1}{6}\)
Answer:
The value of \(\frac{4}{3}\) × \(\frac{1}{6}\) is greater than \(\frac{1}{6}\) or less than \(\frac{4}{3}\)
Explanation:
The given fractions are: \(\frac{4}{3}\) and \(\frac{1}{6}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
Now,
\(\frac{4}{3}\) is greater than 1
\(\frac{1}{6}\) is less than 1
So,
\(\frac{4}{3}\) × \(\frac{1}{6}\) is less than \(\frac{4}{3}\)
Hence, from the above,
We can conclude that the value of \(\frac{4}{3}\) × \(\frac{1}{6}\) is greater than \(\frac{1}{6}\) or less than \(\frac{4}{3}\)
Apply and Grow
Without calculating, tell whether the product is less than, greater than, or equal to each of its factors.
Question 4.
\(\frac{1}{4}\) × \(\frac{1}{12}\)
Answer:
The value of \(\frac{1}{4}\) × \(\frac{1}{12}\) is less than 1
Explanation:
The given fractions are: latex]\frac{1}{4}[/latex] and \(\frac{1}{12}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{1}{4}\) is less than 1
\(\frac{1}{12}\) is less than 1
So,
\(\frac{1}{4}\) × \(\frac{1}{12}\) is less than 1
Hence, from the above,
We can conclude that the value of \(\frac{1}{4}\) × \(\frac{1}{12}\) is less than 1
Question 5.
3\(\frac{4}{5}\) × 6\(\frac{7}{8}\)
Answer:
The value of 3\(\frac{4}{5}\) × 6\(\frac{7}{8}\) is greater than 1
Explanation:
The given fractions are: 3\(\frac{4}{5}\) and 6\(\frac{7}{8}\)
The representation of 3\(\frac{4}{5}\) and 6\(\frac{7}{8}\) in the improper fractions form is: \(\frac{19}{5}\) and \(\frac{55}{8}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{19}{5}\) is greater than 1
\(\frac{55}{8}\) is greater than 1
So,
3\(\frac{4}{5}\) × 6\(\frac{7}{8}\) is greater than 1
Hence, from the above,
We can conclude that the value of 3\(\frac{4}{5}\) × 6\(\frac{7}{8}\) is greater than 1
Question 6.
\(\frac{1}{6}\) × \(\frac{10}{10}\)
Answer:
The value of \(\frac{1}{6}\) × \(\frac{10}{10}\) is less than 1
Explanation:
The given fractions are: \(\frac{1}{6}\) and \(\frac{10}{10}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
We know that,
\(\frac{10}{10}\) is 1
So,
\(\frac{1}{6}\) is less than 1
So,
\(\frac{1}{6}\) × \(\frac{10}{10}\) is less than 1
Hence, from the above,
We can conclude that the value of \(\frac{1}{6}\) × \(\frac{10}{10}\) is less than 1
Question 7.
\(\frac{2}{3}\) × 5
Answer:
The value of \(\frac{2}{3}\) × 5 is less than 5
Explanation:
The given fractions are: \(\frac{2}{3}\) and 5
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{2}{3}\) is less than 1
So,
\(\frac{2}{3}\) × 5 is less than 5
Hence, from the above,
We can conclude that the value of \(\frac{2}{3}\) × 5 is less than 5
Question 8.
\(\frac{7}{10}\) × 4\(\frac{8}{9}\)
Answer:
The value of \(\frac{7}{10}\) × 4\(\frac{8}{9}\) is greater than 1
Explanation:
The given fractions are: \(\frac{7}{10}\) and 4\(\frac{8}{9}\)
The representation of 4\(\frac{8}{9}\) in the improper fraction form is: \(\frac{44}{9}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{7}{10}\) is less than 1
\(\frac{44}{9}\) is greater than 1
So,
\(\frac{7}{10}\) × 4\(\frac{8}{9}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{7}{10}\) × 4\(\frac{8}{9}\) is greater than 1
Question 9.
\(\frac{9}{2}\) × 1\(\frac{3}{4}\)
Answer:
The value of \(\frac{9}{2}\) × 1\(\frac{3}{4}\) is greater than 1
Explanation:
The given fractions are: \(\frac{9}{2}\) × 1\(\frac{3}{4}\)
The representation of 1\(\frac{3}{4}\) in the improper fraction form is: \(\frac{7}{4}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{9}{2}\) is greater than 1
\(\frac{7}{4}\) is greater than 1
So,
\(\frac{9}{2}\) × 1\(\frac{3}{4}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{9}{2}\) × 1\(\frac{3}{4}\) is greater than 1
Without calculating, order the products from least to greatest.
Question 10.
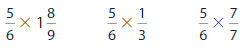
Answer:
The order of products from the least to the greatest is:
\(\frac{5}{6}\) × \(\frac{1}{3}\) < \(\frac{5}{6}\) × \(\frac{7}{7}\) < \(\frac{5}{6}\) × 1\(\frac{8}{9}\)
Explanation:
The given products are:
A) \(\frac{5}{6}\) × \(\frac{1}{3}\)
B) \(\frac{5}{6}\) × \(\frac{7}{7}\)
C) \(\frac{5}{6}\) × 1\(\frac{8}{9}\)
So,
In A),
\(\frac{5}{6}\) and \(\frac{1}{3}\) are less than 1
So,
\(\frac{5}{6}\) × \(\frac{1}{3}\) is less than 1
In B),
\(\frac{5}{6}\) is less than 1
\(\frac{7}{7}\) is 1
So,
\(\frac{5}{6}\) × \(\frac{7}{7}\) is less than 1
In C),
\(\frac{5}{6}\) is less than1
The representation of 1\(\frac{8}{9}\) in the improper fraction form is: \(\frac{17}{9}\)
So,
\(\frac{17}{9}\) is greater than 1
So,
\(\frac{5}{6}\) × 1\(\frac{8}{9}\) is greater than 1
Hence, from the above,
We can conclude that the order of the products from the least to the greatest is:
\(\frac{5}{6}\) × \(\frac{1}{3}\) < \(\frac{5}{6}\) × \(\frac{7}{7}\) < \(\frac{5}{6}\) × 1\(\frac{8}{9}\)
Question 11.
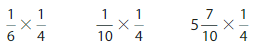
Answer:
The order of products from the least to the greatest is:
\(\frac{1}{6}\) × \(\frac{1}{4}\) < \(\frac{1}{10}\) × \(\frac{1}{4}\) < 5\(\frac{7}{10}\) × \(\frac{1}{4}\)
Explanation:
The given products are:
A) \(\frac{1}{6}\) × \(\frac{1}{4}\)
B) \(\frac{1}{10}\) × \(\frac{1}{4}\)
C) \(\frac{1}{4}\) × 5\(\frac{7}{10}\)
So,
In A),
\(\frac{1}{6}\) and \(\frac{1}{4}\) are less than 1
So,
\(\frac{1}{6}\) × \(\frac{1}{4}\) is less than 1
In B),
\(\frac{1}{10}\) is less than 1
\(\frac{1}{4}\) is less than 1
So,
\(\frac{1}{10}\) × \(\frac{1}{4}\) is less than 1
In C),
\(\frac{1}{4}\) is less than1
The representation of 5\(\frac{7}{10}\) in the improper fraction form is: \(\frac{57}{10}\)
So,
\(\frac{57}{10}\) is greater than 1
So,
\(\frac{1}{4}\) × 5\(\frac{7}{10}\) is greater than 1
Hence, from the above,
We can conclude that the order of the products from the least to the greatest is:
\(\frac{1}{6}\) × \(\frac{1}{4}\) < \(\frac{1}{10}\) × \(\frac{1}{4}\) < 5\(\frac{7}{10}\) × \(\frac{1}{4}\)
Question 12.
YOU BE THE TEACHER
Your friend says that \(\frac{1}{2}\) × 8 is half as much as 8. Is your friend correct? Explain.
Answer:
Yes, your friend is correct
Explanation:
The given numbers are: \(\frac{1}{2}\) and 8
So,
\(\frac{1}{2}\) × 8 = \(\frac{1}{2}\) × \(\frac{8}{1}\)
= \(\frac{1 × 8}{2 × 1}\)
= 4
It is also given that according to your friend,
\(\frac{1}{2}\) × 8 is half as much as 8.
So,
8 ÷ 2 = 4
Hence, from the above,
We can conclude that your friend is correct.
Question 13.
DIG DEEPER!
Without calculating, tell whether the product is less than, greater than, or equal to 3\(\frac{3}{4}\). Explain.
\(\left(\frac{1}{2} \times 3 \frac{3}{4}\right)\) × \(\frac{2}{7}\)
Answer:
\(\left(\frac{1}{2} \times 3 \frac{3}{4}\right)\) × \(\frac{2}{7}\) is less than 3\(\frac{3}{4}\)
Explanation:
The representation of 3\(\frac{3}{4}\) in the improper fraction form is: \(\frac{15}{4}\)
Now,
\(\left(\frac{1}{2} \times 3 \frac{3}{4}\right)\) × \(\frac{2}{7}\)
= ( \(\frac{1}{2}\) × \(\frac{15}{4}\) ) × \(\frac{2}{7}\)
= \(\frac{15}{8}\) × \(\frac{2}{7}\)
= \(\frac{2 × 15}{7 × 8}\)
= \(\frac{30}{56}\)
= \(\frac{15}{28}\)
Now,
\(\frac{15}{4}\) is multiplied by \(\frac{7}{7}\)
So,
\(\frac{15}{4}\) = \(\frac{105}{28}\)
So,
When we compare \(\frac{105}{28}\) and \(\frac{15}{28}\)
We will get \(\frac{105}{28}\) is greater
Hence, from the above,
We can conclude that \(\left(\frac{1}{2} \times 3 \frac{3}{4}\right)\) × \(\frac{2}{7}\) is less than 3\(\frac{3}{4}\)
Think and Grow: Modeling Real Life
Example
Men’s shot put competitions use a shot with a mass of 7\(\frac{1}{4}\) kilograms. The mass of a bowling ball is \(\frac{7}{8}\) as much as the mass of the shot. Is the mass of the bowling ball less than, greater than, or equal to the mass of the shot?

Write an expression to represent the mass of the bowling ball.
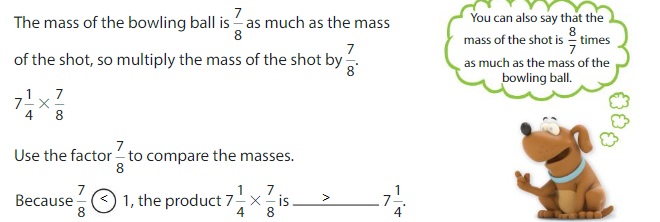
So, the mass of the bowling ball is greater than the mass of the shot.
Show and Grow
Question 14.
You practice playing the keyboard for 3\(\frac{1}{2}\) hours. Your friend practices playing the keyboard for \(\frac{5}{4}\) as many hours as you. Does your friend practice for fewer hours, more hours, or the same number of hours as you?
Answer:
You practice more hours than your friend
Explanation:
It is given that you practice playing the keyboard for 3\(\frac{1}{2}\) hours. Your friend practices playing the keyboard for \(\frac{5}{4}\) as many hours as you.
So,
Now,
The representation of 3\(\frac{1}{2}\) in the improper fraction form is: \(\frac{7}{2}\)
So,
The number of hours you practice playing the keyboard is: \(\frac{7}{2}\) hours
The number of hours your friend practice playing the keyboard is: \(\frac{5}{4}\) hours
So,
For comparison, make the denominators equal.
So,
Multiply \(\frac{7}{2}\) with \(\frac{2}{2}\)
So,
\(\frac{7}{2}\) = \(\frac{14}{4}\)
By comparing the timings ,
We can say that
\(\frac{14}{4}\) > \(\frac{5}{4}\)
Hence, from the above,
We can conclude that you practice more hours than your friend
Question 15.
The original price of a telescope is $99. The sale price is \(\frac{4}{5}\) of the original price. An astrologist buys the telescope at its sale price and uses a half-off-coupon. What fraction of the original price does the astrologist pay for the telescope?
Answer:
The fraction of the original price the astrologist pays for the telescope is: \(\frac{4}{10}\)
Explanation:
It is given that the original price of a telescope is $99. The sale price is \(\frac{4}{5}\) of the original price. and an astrologist buys the telescope at its sale price and uses a half-off-coupon.
So,
The cost of the telescope that an astrologist bought = ( The \(\frac{4}{5}\)th of the original price ) × ( Half-off -coupon on the \(\frac{4}{5}\)th of the original price )
= \(\frac{4}{5}\) × \(\frac{1}{2}\)
= \(\frac{4 × 1}{5 × 2}\)
= \(\frac{4}{10}\)
Hence, from the above,
We can conclude that the fraction of the original price the astrologist pays for the telescope is: \(\frac{4}{10}\)
Question 16.
The Abraj Al-Bait Clock Tower is \(\frac{6}{10}\) kilometer tall. Zifeng Tower is \(\frac{3}{4}\) as tall as the clock tower. Is Zifeng Tower shorter than, taller than, or the same height as the Abraj Al-Bait Clock Tower? What is the height of each tower in meters?

Answer:
The Abraj al-Bait Clock tower is taller than the Zifeng tower
The height of Abraj al-Bait Clock tower is: \(\frac{24}{40}\)
The height of Zifeng tower is: \(\frac{18}{40}\)
Explanation:
It is given that the Abraj Al-Bait Clock Tower is \(\frac{6}{10}\) kilometer tall and Zifeng Tower is \(\frac{3}{4}\) as tall as the clock tower.
So,
The height of Abraj al-Bait Clock tower is: \(\frac{6}{10}\) kilometer
Now,
The height of Zifeng tower is = \(\frac{6}{10}\) × \(\frac{3}{4}\)
= \(\frac{6 × 3}{10 × 4}\)
= \(\frac{18}{40}\)
Now, for comparison, make the denomonators of both the towers equal.
So,
\(\frac{6}{10}\) is multiplied by \(\frac{4}{4}\)
So,
\(\frac{6}{10}\) = \(\frac{24}{40}\)
By comparing the heights of the two towers,
We can say that
\(\frac{24}{40}\) > \(\frac{18}{40}\)
Hence, from the above,
We can conclude that
The Abraj al-Bait Clock tower is taller than the Zifeng tower
The height of Abraj al-Bait Clock tower is: \(\frac{24}{40}\)
The height of Zifeng tower is: \(\frac{18}{40}\)
Compare Factors and Products Homework & Practice 9.8
Without calculating, tell whether the product is less than, greater than, or equal to each of its factors.
Question 1.
1\(\frac{3}{4}\) × 6
Answer:
The value of 1\(\frac{3}{4}\) × 6 is greater than 6
Explanation:
The given numbers are: 1\(\frac{3}{4}\) and 6
The representation of 1\(\frac{3}{4}\) in the improper fraction form is: \(\frac{7}{4}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{7}{4}\) is greater than 1
So,
1\(\frac{3}{4}\) × 6 is greater than 6
Hence, from the above,
We can conclude that the value of 1\(\frac{3}{4}\) × 6 is greater than 6
Question 2.
\(\frac{5}{12}\) × \(\frac{1}{6}\)
Answer:
The value of \(\frac{5}{12}\) × \(\frac{1}{6}\) is less than 1
Explanation;
The given fractions are: \(\frac{5}{12}\) and \(\frac{1}{6}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{5}{12}\) is less than 1
\(\frac{1}{6}\) is less than 1
So,
\(\frac{5}{12}\) × \(\frac{1}{6}\) is less than 1
Hence, from the above,
We can conclude that the value of \(\frac{5}{12}\) × \(\frac{1}{6}\) is less than 1
Question 3.
\(\frac{2}{7}\) × \(\frac{5}{5}\)
Answer:
The value of \(\frac{2}{7}\) × \(\frac{5}{5}\) is less than 1
Explanation:
The given fractions are: \(\frac{2}{7}\) and \(\frac{5}{5}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{2}{7}\) is less than 1
We know that
\(\frac{5}{5}\) is 1
So,
\(\frac{2}{7}\) × \(\frac{5}{5}\) is less than 1
Hence, from the above,
We can conclude that the value of \(\frac{2}{7}\) × \(\frac{5}{5}\) is less than 1
Question 4.
3\(\frac{4}{5}\) × 2\(\frac{9}{10}\)
Answer:
The value of 3\(\frac{4}{5}\) × 2\(\frac{9}{10}\) is greater than 1
Explanation:
the given mixed fractions are: 3\(\frac{4}{5}\) and 2\(\frac{9}{10}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
The representation of the mixed numbers in the fraction form is: \(\frac{19}{5}\) and \(\frac{29}{10}\)
So,
\(\frac{19}{5}\) is greater than 1
\(\frac{29}{10}\) is greater than
So,
3\(\frac{4}{5}\) × 2\(\frac{9}{10}\) is greater than 1
Hence, from the above,
We can conclude that the value of 3\(\frac{4}{5}\) × 2\(\frac{9}{10}\) is greater than 1
Question 5.
8 × \(\frac{2}{3}\)
Answer:
The value of 8 is greater than \(\frac{2}{3}\)
Explanation:
The given numbers are: 8 and \(\frac{2}{3}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{2}{3}\) is less than 1
So,
8 is greater than \(\frac{2}{3}\)
Hence, from the above,
We can conclude that the value of 8 is greater than \(\frac{2}{3}\)
Question 6.
1\(\frac{7}{8}\) × \(\frac{1}{4}\)
Answer:
The value of 1\(\frac{7}{8}\) × \(\frac{1}{4}\) is less than 1
Explanation:
The given fractions are: 1\(\frac{7}{8}\) and \(\frac{1}{4}\)
The representation of 1\(\frac{7}{8}\) in the fraction form is: \(\frac{15}{8}\)
We know that,
When you multiply a number by a fraction greater than 1, the product is greater than the number. When you multiply a number by a fraction less than 1, the product is less than the number.
So,
\(\frac{15}{8}\) is greater than 1
\(\frac{1}{4}\) is less than 1
So,
1\(\frac{7}{8}\) × \(\frac{1}{4}\) is less than 1
Hence, from the above,
We can conclude that the value of 1\(\frac{7}{8}\) × \(\frac{1}{4}\) is less than 1
Without calculating, order the products from least to greatest.
Question 7.
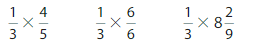
Answer:
The order of products from the least to the greatest is:
\(\frac{1}{3}\) × \(\frac{4}{5}\) < \(\frac{1}{3}\) × \(\frac{6}{6}\) < 8\(\frac{2}{9}\) × \(\frac{1}{3}\)
Explanation:
The given products are:
A) \(\frac{1}{3}\) × \(\frac{4}{5}\)
B) \(\frac{1}{3}\) × \(\frac{6}{6}\)
C) 8\(\frac{2}{9}\) × \(\frac{1}{3}\)
So,
In A),
\(\frac{1}{3}\) and \(\frac{4}{5}\) are less than 1
So,
\(\frac{1}{3}\) × \(\frac{4}{5}\) is less than 1
In B),
\(\frac{1}{3}\) is less than 1
\(\frac{6}{6}\) is 1
So,
\(\frac{1}{3}\) × \(\frac{6}{6}\) is less than 1
In C),
\(\frac{1}{3}\) is less than1
The representation of 8\(\frac{2}{9}\) in the improper fraction form is: \(\frac{74}{9}\)
So,
\(\frac{74}{9}\) is greater than 1
So,
\(\frac{1}{3}\) × 8\(\frac{2}{9}\) is greater than 1
Hence, from the above,
We can conclude that the order of the products from the least to the greatest is:
\(\frac{1}{3}\) × \(\frac{4}{5}\) < \(\frac{1}{3}\) × \(\frac{6}{6}\) < 8\(\frac{2}{9}\) × \(\frac{1}{3}\)
Question 8.
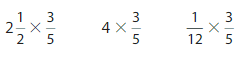
Answer:
The order of products from the least to the greatest is:
\(\frac{1}{12}\) × \(\frac{3}{5}\) < 4 × \(\frac{3}{5}\) < 2\(\frac{1}{2}\) × \(\frac{3}{5}\)
Explanation:
The given products are:
A) \(\frac{1}{12}\) × \(\frac{3}{5}\)
B) 4 × \(\frac{3}{5}\)
C) 2\(\frac{1}{2}\) × \(\frac{3}{5}\)
So,
In A),
\(\frac{1}{12}\) and \(\frac{3}{5}\) are less than 1
So,
\(\frac{1}{12}\) × \(\frac{3}{5}\) is less than 1
In B),
\(\frac{3}{5}\) is less than 1
So,
4 × \(\frac{3}{5}\) is less than 4
In C),
\(\frac{3}{5}\) is less than1
The representation of 2\(\frac{1}{2}\) in the improper fraction form is: \(\frac{5}{2}\)
So,
\(\frac{5}{2}\) is greater than 1
So,
\(\frac{3}{5}\) × 2\(\frac{1}{2}\) is greater than 1
Hence, from the above,
We can conclude that the order of the products from the least to the greatest is:
\(\frac{1}{12}\) × \(\frac{3}{5}\) < 4 × \(\frac{3}{5}\) < 2\(\frac{1}{2}\) × \(\frac{3}{5}\)
Question 9.
Logic
Without calculating, use >, <, or = to make the statement true. Explain.
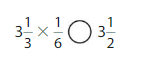
Answer:
The value of 3\(\frac{1}{3}\) × \(\frac{1}{6}\) is less than 3\(\frac{1}{2}\)
Explanation:
The given fractions are: 3\(\frac{1}{3}\), \(\frac{1}{6}\) and 3\(\frac{1}{2}\)
The representations of the 3\(\frac{1}{3}\) and 3\(\frac{1}{2}\) in the fraction form is: \(\frac{7}{2}\) and \(\frac{10}{3}\)
So,
3\(\frac{1}{3}\) × \(\frac{1}{6}\)
= \(\frac{10}{3}\) × \(\frac{1}{6}\)
= \(\frac{10}{18}\)
To compare the fractions, equate the denominators
So,
Multiply \(\frac{7}{2}\) by \(\frac{9}{9}\)
= \(\frac{63}{18}\)
So,
By comparison,
We can say that
\(\frac{10}{18}\) < \(\frac{63}{18}\)
Hence, from the above,
We can conclude that the value of 3\(\frac{1}{3}\) × \(\frac{1}{6}\) is less than 3\(\frac{1}{2}\)
Question 10.
Logic
Without calculating, determine which number makes the statement true.
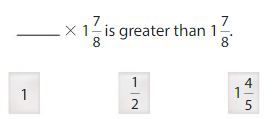
Answer:
Let the missing number be x.
The options for x are given as:
A) 1 B) \(\frac{1}{2}\) and C) 1\(\frac{4}{5}\)
So,
From the given three fractions,
The value of x is: 1\(\frac{4}{5}\)
Explanation:
The given multiplication equation is:
x × 1\(\frac{7}{8}\) is greater than 1\(\frac{7}{8}\)
So,
To find the value of x, there are 3 options. They are:
A) 1 B) \(\frac{1}{2}\) and C) 1\(\frac{4}{5}\)
Now,
Let x = 1\(\frac{4}{5}\)
So,
1\(\frac{4}{5}\) × 1\(\frac{7}{8}\)
= \(\frac{9}{5}\) × \(\frac{15}{8}\)
= \(\frac{27}{8}\)
So, by comparison,
We will get,
\(\frac{27}{8}\) is greater than \(\frac{15}{8}\)
Hence, from the above,
We can conclude that the missing number is: 1\(\frac{4}{5}\)
Question 11.
Reasoning
Why does multiplying by a fraction greater than one result in a product greater than the original number?
Answer:
In the given fraction, if the numerator is greater than the denominator, then the given fraction is greater than 1
So,
When the whole number is multiplied by the fraction which is greater than 1, the result in a product will be greater than the original number i.e, the whole number
Question 12.
Modeling Real Life
You snowboard 1\(\frac{7}{8}\) miles. Your friend snowboards 3\(\frac{2}{3}\) times as far as you. Does your friend snowboard fewer miles, more miles, or the same number of miles as you?
Answer:
The number of miles you snowboarded is less than your friend
Explanation:
It is given that you snowboard 1\(\frac{7}{8}\) miles. Your friend snowboards 3\(\frac{2}{3}\) times as far as you.
So,
The number of miles you snowboard is: 1\(\frac{7}{8}\) miles
So,
The number of miles your friend snowboard is = 1\(\frac{7}{8}\) × 3\(\frac{2}{3}\)
= \(\frac{15}{8}\) × \(\frac{11}{3}\)
= \(\frac{15 × 11}{3 × 8}\)
= \(\frac{165}{24}\) miles
So,
For comparison we have to make the denominators equal.
So,
Multiply \(\frac{15}{8}\) by \(\frac{3}{3}\)
So,
\(\frac{15}{8}\) = \(\frac{45}{24}\)
So,
By comparing, we will get
\(\frac{45}{24}\) is less than \(\frac{165}{24}\) miles
Hence, from the above,
We can conclude that the number of miles you snowboarded is less than your friend
Question 13.
Modeling Real Life
A pet owner has three dogs. The youngest dog weighs \(\frac{1}{4}\) as much as the second oldest dog. The oldest dog weighs 1\(\frac{1}{4}\) as much as the second oldest. The second oldest weighs 20 pounds. Which dog weighs the most? the least?

Answer:
The dog that weighs the most is: The oldest dog
The dog that weighs the least is: The youngest dog
Explanation:
It is given that a pet owner has three dogs. The youngest dog weighs \(\frac{1}{4}\) as much as the second oldest dog. The oldest dog weighs 1\(\frac{1}{4}\) as much as the second oldest. The second oldest weighs 20 pounds.
So,
The weight of the second oldest dog is: 20 pounds
Now,
The weight of the oldest dog = 1\(\frac{1}{4}\) × ( The weight of the oldest second dog )
= 1\(\frac{1}{4}\) × 20
= \(\frac{5}{4}\) × 20
= \(\frac{5 × 20}{4 × 1}\)
= 25 pounds
Now,
The weight of the youngest dog = \(\frac{1}{4}\) × ( The weight of the second oldest dog )
= \(\frac{1}{4}\) × 20
= \(\frac{1 × 20}{4}\)
= 5 pounds
Hence, from the above,
We can conclude that
The dog that weighs the most is: The oldest dog
The dog that weighs the least is: The youngest dog
Review & Refresh
Compare.
Question 14.
![]()
Answer:
40.5 is greater than 40.13
Explanation:
The given decimal numbers are: 40.5 and 40.13
For comparison, compare the place value of the given digits
If there are more than 2 digits after the decimal, first compare the tenths position and after that only compare the hundredths position
If we can get the result in the tenths position only, then there is no need for further comparison
Hence, from the above,
We can conclude that 40.5 is greater than 40.13
Question 15.
![]()
Answer:
13.90 is equal to 13.9
Explanation:
The given decimal numbers are: 13.90 and 13.9
For comparison, compare the place value of the given digits
If there are more than 2 digits after the decimal, first compare the tenths position and after that only compare the hundredths position
If we can get the result in the tenths position only, then there is no need for further comparison
Hence, from the above,
We can conclude that 13.90 is equal to 13.9
Question 16.
![]()
Answer:
32.006 is less than 32.06
Explanation:
The given decimal numbers are: 32.006 and 32.06
For comparison, compare the place value of the given digits
If there are more than 2 digits after the decimal, first compare the tenths position and after that only compare the hundredths position
If we can get the result in the tenths position only, then there is no need for further comparison
Hence, from the above,
We can conclude that 32.006 is less than 32.06
Multiply Fractions Performance Task
Question 1.
You see a rock formation at a national park. The formation has layers that formed millions of years ago when particles settled in the water and became rock. You make a model of the rock formation using \(\frac{3}{16}\) -inch foam sheets.
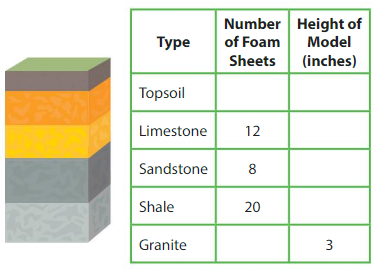
a. The three types of sedimentary rocks are limestone, sandstone, and shale. Use the number of foam sheets to find the height of each sedimentary rock layer.
Answer:
The height of limestone is: \(\frac{9}{4}\) inches
The height of sandstone is: \(\frac{3}{2}\) inches
The height of shale is: \(\frac{15}{4}\) inches
Explanation:
It is given that the height of each foam sheet is: \(\frac{3}{16}\) -inches

From the table,
The number of foam sheets for Limestone is: 12
The number of foam sheets for sandstone is: 8
The number of foam sheets for shale is: 20
So,
The height of limestone is: ( The height of each foam sheet ) × ( The total number of foam sheets )
= \(\frac{3}{16}\) × 12
= \(\frac{3}{16}\) × \(\frac{12}{1}\)
= \(\frac{9}{4}\) inches
The height of sandstone is: ( The height of each foam sheet ) × ( The total number of foam sheets )
= \(\frac{3}{16}\) × 8
= \(\frac{3}{16}\) × \(\frac{8}{1}\)
= \(\frac{3}{2}\) inches
The height of shale is: ( The height of each foam sheet ) × ( The total number of foam sheets )
= \(\frac{3}{16}\) × 20
= \(\frac{3}{16}\) × \(\frac{20}{1}\)
= \(\frac{15}{4}\) inches
Hence, from the above,
We can conclude that
The height of limestone is: \(\frac{9}{4}\) inches
The height of sandstone is: \(\frac{3}{2}\) inches
The height of shale is: \(\frac{15}{4}\) inches
b. What is the combined height of the sedimentary rock layers?
Answer:
The combined height of the sedimentary layers is: \(\frac{15}{2}\) inches
Explanation:
The combined height of the sedimentary rock layers = The height of limestone + The height of sandstone + The height of the shale
= \(\frac{9}{4}\) + \(\frac{3}{2}\) + \(\frac{15}{4}\)
= \(\frac{24}{4}\) + \(\frac{3}{2}\)
= \(\frac{12}{2}\) + \(\frac{3}{2}\)
= \(\frac{15}{2}\) inches
Hence, from the above,
We can conclude that the combined height of the sedimentary layers is: \(\frac{15}{2}\) inches
c. Will you use more foam sheets for the granite layers of the shale layers? Explain.
Answer:
We use more foam sheets for the granite layers
Explanation:
From the above,
The height of the shale layers is: \(\frac{15}{4}\) inches
From the table,
The height of the granite layers is: 3 inches
When we compare the two values,
We can observe that the height of shale layers is greater than the granite layers
Hence, from the above,
We can conclude that we will use more foam sheets for granite layers
d. The height of the topsoil layer is 1\(\frac{1}{4}\) times the height of the sandstone layer. How many foam sheets do you use in the topsoil layer?
Answer:
The height of the topsoil layer is: \(\frac{15}{8}\) inches
Explanation:
From the above,
The height of the sandstone layer is: \(\frac{3}{2}\) inches
So,
The height of topsoil layer = 1\(\frac{1}{4}\) × \(\frac{3}{2}\)
= \(\frac{5}{4}\) × \(\frac{3}{2}\)
= \(\frac{15}{8}\) inches
Hence, from the above,
We can conclude that the height of the topsoil layer is: \(\frac{15}{8}\) inches
e. On your model, 1 inch represents 40 feet. What is the actual height of the rock formation?
Answer:
The actual height of the rock formation is: 495 feet
Explanation:
From the above,
The height of the sedimentary layers is: \(\frac{15}{2}\) inches
The height of the topsoil layer is: \(\frac{15}{8}\) inches
The height of the granite layer is: 3 inches
So,
The combined height of the rock formation = \(\frac{15}{2}\) + \(\frac{15}{8}\) + 3
= \(\frac{99}{8}\) inches
But, it is given that,
1 inch = 40 feet
So,
The combined height of the rock formation in feet = \(\frac{99}{8}\) inches × 40
= 495 feet
Hence, from the above,
We can conclude that the height of the rock formation in feet is: 495 feet
f. Why do you think the rock formation has layers?
Answer:
The rock formation has layers because of the tectonic plates.
Multiply Fractions Activity
Fraction Connection: Multiplication
Directions:
1. Players take turns rolling three dice.
2. On your turn, evaluate the expression indicated by your roll and cover the answer.
3. The first player to get four in a row, horizontally, vertically, or diagonally, wins?
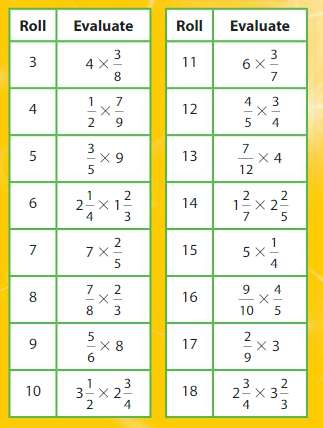
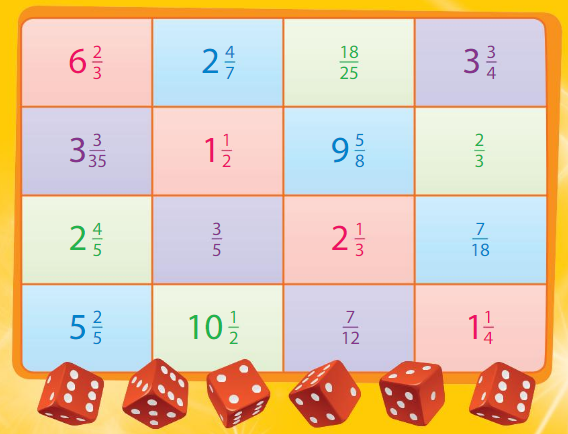
Multiply Fractions Chapter Practice
9.1 Multiply Whole Numbers by Fractions
Multiply.
Question 1.
5 × \(\frac{1}{2}\) = _______
Answer:
5 × \(\frac{1}{2}\) = \(\frac{5}{2}\)
Explanation:
The given numbers are: 5 and \(\frac{1}{2}\)
So,
5 × \(\frac{1}{2}\)
= \(\frac{5}{1}\) × \(\frac{1}{2}\)
= \(\frac{5 × 1}{1 × 2}\)
= \(\frac{5}{2}\)
Hence,
5 × \(\frac{1}{2}\) = \(\frac{5}{2}\)
Question 2.
2 × \(\frac{7}{10}\) = _______
Answer:
2 × \(\frac{7}{10}\) = \(\frac{14}{10}\)
Explanation:
The given numbers are: 2 and \(\frac{7}{10}\)
So,
2 × \(\frac{7}{10}\)
= \(\frac{2}{1}\) × \(\frac{7}{10}\)
= \(\frac{2 × 7}{1 × 10}\)
= \(\frac{14}{10}\)
Hence,
2 × \(\frac{7}{10}\) = \(\frac{14}{10}\)
Question 3.
9 × \(\frac{5}{8}\) = _______
Answer:
9 × \(\frac{5}{8}\) = \(\frac{45}{8}\)
Explanation:
The given numbers are: 9 and \(\frac{5}{8}\)
So,
9 × \(\frac{5}{8}\)
= \(\frac{9}{1}\) × \(\frac{5}{8}\)
= \(\frac{5 × 9}{1 × 8}\)
= \(\frac{45}{8}\)
Hence,
9 × \(\frac{5}{8}\) = \(\frac{45}{8}\)
Question 4.
6 × \(\frac{71}{100}\) = _______
Answer:
6 × \(\frac{71}{100}\) = \(\frac{426}{100}\)
Explanation:
The given numbers are: 6 and \(\frac{71}{100}\)
So,
6 × \(\frac{71}{100}\)
= \(\frac{6}{1}\) × \(\frac{71}{100}\)
= \(\frac{6 × 71}{1 × 100}\)
= \(\frac{426}{100}\)
Hence,
6 × \(\frac{71}{100}\) = \(\frac{426}{100}\)
Question 5.
4 × \(\frac{8}{5}\) = _______
Answer:
4 × \(\frac{8}{5}\) = \(\frac{32}{5}\)
Explanation:
The given numbers are: 4 and \(\frac{8}{5}\)
So,
4 × \(\frac{8}{5}\)
= \(\frac{4}{1}\) × \(\frac{8}{5}\)
= \(\frac{4 × 8}{1 × 5}\)
= \(\frac{32}{5}\)
Hence,
4 × \(\frac{8}{5}\) = \(\frac{32}{5}\)
Question 6.
7 × \(\frac{5}{3}\) = _______
Answer:
7 × \(\frac{5}{3}\) = \(\frac{35}{3}\)
Explanation:
The given numbers are: 7 and \(\frac{5}{3}\)
So,
7 × \(\frac{5}{3}\)
= \(\frac{7}{1}\) × \(\frac{5}{3}\)
= \(\frac{5 × 7}{1 × 3}\)
= \(\frac{35}{3}\)
Hence,
7 × \(\frac{5}{3}\) = \(\frac{35}{3}\)
9.2 Use Models to Multiply Fractions by Whole Numbers
Multiply. Use a model to help.
Question 7.
\(\frac{2}{5}\) of 20
Answer:
20 × \(\frac{2}{5}\) = 8
Explanation:
The given numbers are: 20 and \(\frac{2}{5}\)
So,
20 × \(\frac{2}{5}\)
= \(\frac{20}{1}\) × \(\frac{2}{5}\)
= \(\frac{20 × 2}{1 × 5}\)
= \(\frac{8}{1}\)
= 8
Hence,
20 × \(\frac{2}{5}\) = 8
Question 8.
\(\frac{1}{6}\) × 12
Answer:
12 × \(\frac{1}{6}\) = 2
Explanation:
The given numbers are: 12 and \(\frac{1}{6}\)
So,
12 × \(\frac{1}{6}\)
= \(\frac{12}{1}\) × \(\frac{1}{6}\)
= \(\frac{12 × 1}{1 × 6}\)
= \(\frac{2}{1}\)
= 2
Hence,
12 × \(\frac{1}{6}\) = 2
Question 9.
\(\frac{1}{3}\) × 6
Answer:
6 × \(\frac{1}{3}\) = 2
Explanation:
The given numbers are: 6 and \(\frac{1}{3}\)
So,
6 × \(\frac{1}{3}\)
= \(\frac{6}{1}\) × \(\frac{1}{3}\)
= \(\frac{6 × 1}{1 × 3}\)
= \(\frac{2}{1}\)
= 2
Hence,
6 × \(\frac{1}{3}\) = 2
Question 10.
\(\frac{5}{16}\) of 8
Answer:
8 × \(\frac{5}{16}\) = \(\frac{5}{2}\)
Explanation:
The given numbers are: 8 and \(\frac{5}{16}\)
So,
8 × \(\frac{5}{16}\)
= \(\frac{8}{1}\) × \(\frac{5}{16}\)
= \(\frac{5 × 8}{1 × 16}\)
= \(\frac{5}{2}\)
Hence,
8 × \(\frac{5}{16}\) = \(\frac{5}{2}\)
Question 11.
Modeling Real Life
You have 24 apples. You use \(\frac{1}{4}\) of them to make a single serving of applesauce. How many apples do you not use?

Answer:
The number of apples you do not use is: 18 apples
Explanation:
It is given that you have 24 apples and you use \(\frac{1}{4}\) of them to make a single serving of applesauce.
So,
The number of apples you used = ( The total number of apples ) × ( The fraction of apples you used to make a single serving of applesauce )
= 24 × \(\frac{1}{4}\)
= \(\frac{24}{1}\) × \(\frac{1}{4}\)
= \(\frac{6}{1}\)
= 6 apples
Now,
The number of apples that do not use = ( The total number of apples ) – ( The number of apples you used )
= 24 – 6
= 18 apples
Hence, from the above,
We can conclude that the number of apples that do not use is: 18 apples
9.3 Multiply Fractions and Whole Numbers
Multiply.
Question 12.
\(\frac{3}{5}\) × 15 = _______
Answer:
15 × \(\frac{3}{5}\) = 9
Explanation:
The given numbers are: 15 and \(\frac{3}{5}\)
So,
15 × \(\frac{3}{5}\)
= \(\frac{15}{1}\) × \(\frac{3}{5}\)
= \(\frac{15 × 3}{1 × 5}\)
= \(\frac{9}{1}\)
= 9
Hence,
15 × \(\frac{3}{5}\) = 9
Question 13.
\(\frac{9}{10}\) × 30 = _______
Answer:
30 × \(\frac{9}{10}\) = 27
Explanation:
The given numbers are: 30 and \(\frac{9}{10}\)
So,
30 × \(\frac{9}{10}\)
= \(\frac{30}{1}\) × \(\frac{9}{10}\)
= \(\frac{30 × 9}{1 × 10}\)
= \(\frac{27}{1}\)
= 27
Hence,
30 × \(\frac{9}{10}\) = 27
Question 14.
48 × \(\frac{3}{4}\) = _______
Answer:
48 × \(\frac{3}{4}\) = 36
Explanation:
The given numbers are: 48 and \(\frac{3}{4}\)
So,
48 × \(\frac{3}{4}\)
= \(\frac{48}{1}\) × \(\frac{3}{4}\)
= \(\frac{48 × 3}{1 × 4}\)
= \(\frac{36}{1}\)
= 36
Hence,
48 × \(\frac{3}{4}\) = 36
Question 15.
11 × \(\frac{5}{9}\) = _______
Answer:
11 × \(\frac{5}{9}\) = \(\frac{55}{9}\)
Explanation:
The given numbers are: 11 and \(\frac{5}{9}\)
So,
11 × \(\frac{5}{9}\)
= \(\frac{11}{1}\) × \(\frac{5}{9}\)
= \(\frac{5 × 11}{1 × 9}\)
= \(\frac{55}{9}\)
Hence,
11 × \(\frac{5}{9}\) = \(\frac{55}{9}\)
Question 16.
\(\frac{1}{6}\) × 19 = _______
Answer:
19 × \(\frac{1}{6}\) = \(\frac{19}{6}\)
Explanation:
The given numbers are: 19 and \(\frac{1}{6}\)
So,
19 × \(\frac{1}{6}\)
= \(\frac{19}{1}\) × \(\frac{1}{6}\)
= \(\frac{19 × 1}{1 × 6}\)
= \(\frac{19}{6}\)
Hence,
19 × \(\frac{1}{6}\) = \(\frac{19}{6}\)
Question 17.
7 × \(\frac{13}{50}\) = _______
Answer:
7 × \(\frac{13}{50}\) = \(\frac{91}{50}\)
Explanation:
The given numbers are: 7 and \(\frac{13}{50}\)
So,
7 × \(\frac{13}{50}\)
= \(\frac{7}{1}\) × \(\frac{13}{50}\)
= \(\frac{7 × 13}{1 × 50}\)
= \(\frac{91}{50}\)
Hence,
7 × \(\frac{13}{50}\) = \(\frac{91}{50}\)
9.4 Use Models to Multiply Fractions
Multiply. Use a model to help.
Question 18.
\(\frac{1}{2}\) × \(\frac{1}{10}\) = _______
Answer:
\(\frac{1}{2}\) × \(\frac{1}{10}\) = \(\frac{1}{20}\)
Explanation:
The given numbers are: \(\frac{1}{2}\) and \(\frac{1}{10}\)
So,
\(\frac{1}{2}\) × \(\frac{1}{10}\)
= \(\frac{1 × 1}{2 × 10}\)
= \(\frac{1}{20}\)
Hence,
\(\frac{1}{2}\) × \(\frac{1}{10}\) = \(\frac{1}{20}\)
Question 19.
\(\frac{1}{5}\) × \(\frac{1}{9}\) = _______
Answer:
\(\frac{1}{5}\) × \(\frac{1}{9}\) = \(\frac{1}{45}\)
Explanation:
The given numbers are: \(\frac{1}{5}\) and \(\frac{1}{9}\)
So,
\(\frac{1}{5}\) × \(\frac{1}{9}\)
= \(\frac{1 × 1}{5 × 9}\)
= \(\frac{1}{45}\)
Hence,
\(\frac{1}{5}\) × \(\frac{1}{9}\) = \(\frac{1}{45}\)
Question 20.
\(\frac{1}{6}\) × \(\frac{1}{7}\) = _______
Answer:
\(\frac{1}{6}\) × \(\frac{1}{7}\) = \(\frac{1}{42}\)
Explanation:
The given numbers are: \(\frac{1}{6}\) and \(\frac{1}{7}\)
So,
\(\frac{1}{6}\) × \(\frac{1}{7}\)
= \(\frac{1 × 1}{6 × 7}\)
= \(\frac{1}{42}\)
Hence,
\(\frac{1}{6}\) × \(\frac{1}{7}\) = \(\frac{1}{42}\)
Question 21.
\(\frac{1}{3}\) × \(\frac{1}{8}\) = _______
Answer:
\(\frac{1}{3}\) × \(\frac{1}{8}\) = \(\frac{1}{24}\)
Explanation:
The given numbers are: \(\frac{1}{3}\) and \(\frac{1}{8}\)
So,
\(\frac{1}{3}\) × \(\frac{1}{8}\)
= \(\frac{1 × 1}{3 × 8}\)
= \(\frac{1}{24}\)
Hence,
\(\frac{1}{3}\) × \(\frac{1}{8}\) = \(\frac{1}{24}\)
Question 22.
\(\frac{2}{5}\) × \(\frac{1}{3}\) = _______
Answer:
\(\frac{2}{5}\) × \(\frac{1}{3}\) = \(\frac{2}{15}\)
Explanation:
The given numbers are: \(\frac{2}{5}\) and \(\frac{1}{3}\)
So,
\(\frac{2}{5}\) × \(\frac{1}{3}\)
= \(\frac{2 × 1}{5 × 3}\)
= \(\frac{2}{15}\)
Hence,
\(\frac{2}{5}\) × \(\frac{1}{3}\) = \(\frac{2}{15}\)
Question 23.
\(\frac{2}{3}\) × \(\frac{3}{5}\) = _______
Answer:
\(\frac{2}{3}\) × \(\frac{3}{5}\) = \(\frac{2}{5}\)
Explanation:
The given numbers are: \(\frac{2}{3}\) and \(\frac{3}{5}\)
So,
\(\frac{2}{3}\) × \(\frac{3}{5}\)
= \(\frac{2 × 3}{3 × 5}\)
= \(\frac{2}{5}\)
Hence,
\(\frac{2}{3}\) × \(\frac{3}{5}\) = \(\frac{2}{5}\)
9.5 Multiply Fractions
Evaluate.
Question 24.
\(\frac{1}{3}\) × \(\frac{1}{8}\) = _______
Answer:
\(\frac{1}{3}\) × \(\frac{1}{8}\) = \(\frac{1}{24}\)
Explanation:
The given numbers are: \(\frac{1}{3}\) and \(\frac{1}{8}\)
So,
\(\frac{1}{3}\) × \(\frac{1}{8}\)
= \(\frac{1 × 1}{3 × 8}\)
= \(\frac{1}{24}\)
Hence,
\(\frac{1}{3}\) × \(\frac{1}{8}\) = \(\frac{1}{24}\)
Question 25.
\(\frac{5}{6}\) × \(\frac{1}{4}\) = _______
Answer:
\(\frac{5}{6}\) × \(\frac{1}{4}\) = \(\frac{5}{24}\)
Explanation:
The given numbers are: \(\frac{5}{6}\) and \(\frac{1}{4}\)
So,
\(\frac{5}{6}\) × \(\frac{1}{4}\)
= \(\frac{5 × 1}{6 × 4}\)
= \(\frac{5}{24}\)
Hence,
\(\frac{5}{6}\) × \(\frac{1}{4}\) = \(\frac{5}{24}\)
Question 26.
\(\frac{7}{2}\) × \(\frac{2}{5}\) = _______
Answer:
\(\frac{7}{2}\) × \(\frac{2}{5}\) = \(\frac{7}{5}\)
Explanation:
The given numbers are: \(\frac{7}{2}\) and \(\frac{2}{5}\)
So,
\(\frac{7}{2}\) × \(\frac{2}{5}\)
= \(\frac{7 × 2}{2 × 5}\)
= \(\frac{7}{5}\)
Hence,
\(\frac{7}{2}\) × \(\frac{2}{5}\) = \(\frac{7}{5}\)
Question 27.
\(\frac{9}{10}\) × \(\frac{3}{7}\) = _______
Answer:
\(\frac{9}{10}\) × \(\frac{3}{7}\) = \(\frac{27}{70}\)
Explanation:
The given numbers are: \(\frac{9}{10}\) and \(\frac{3}{7}\)
So,
\(\frac{9}{10}\) × \(\frac{3}{7}\)
= \(\frac{9 × 3}{7 × 10}\)
= \(\frac{27}{70}\)
Hence,
\(\frac{9}{10}\) × \(\frac{3}{7}\) = \(\frac{27}{70}\)
Question 28.
\(\frac{4}{5}\) × \(\frac{13}{100}\) = _______
Answer:
\(\frac{4}{5}\) × \(\frac{13}{100}\) = \(\frac{52}{500}\)
Explanation:
The given numbers are: \(\frac{4}{5}\) and \(\frac{13}{100}\)
So,
\(\frac{4}{5}\) × \(\frac{13}{100}\)
= \(\frac{4 × 13}{5 × 100}\)
= \(\frac{52}{500}\)
Hence,
\(\frac{4}{5}\) × \(\frac{13}{100}\) = \(\frac{52}{500}\)
Question 29.
\(\frac{11}{25}\) × \(\frac{3}{4}\) = _______
Answer:
\(\frac{11}{25}\) × \(\frac{3}{4}\) = \(\frac{33}{100}\)
Explanation:
The given numbers are: \(\frac{11}{25}\) and \(\frac{3}{4}\)
So,
\(\frac{11}{25}\) × \(\frac{3}{4}\)
= \(\frac{11 × 3}{25 × 4}\)
= \(\frac{33}{100}\)
Hence,
\(\frac{11}{25}\) × \(\frac{3}{4}\) = \(\frac{33}{100}\)
Question 30.
9 × \(\left(\frac{2}{9} \times \frac{1}{2}\right)\) = _______
Answer:
9 × ( \(\frac{1}{2}\) × \(\frac{2}{9}\) ) = 1
Explanation:
The given numbers are: 9, \(\frac{1}{2}\) and \(\frac{2}{9}\)
So,
9 × (\(\frac{1}{2}\) × \(\frac{2}{9}\) )
= 9 × (\(\frac{1 × 2}{2 × 9}\) )
= 9 × \(\frac{1}{9}\)
= 1
Hence,
9 × ( \(\frac{1}{2}\) × \(\frac{2}{9}\) ) = 1
Question 31.
\(\left(\frac{1}{10}+\frac{7}{10}\right)\) × \(\frac{3}{4}\) = _______
Answer:
\(\left(\frac{1}{10}+\frac{7}{10}\right)\) × \(\frac{3}{4}\) = \(\frac{3}{5}\)
Explanation:
The given fractions are: \(\frac{1}{10}\), \(\frac{7}{10}\) and \(\frac{3}{4}\)
So,
\(\frac{3}{4}\) × (\(\frac{1}{10}\) + \(\frac{7}{10}\) )
= \(\frac{3}{4}\) × (\(\frac{7 × 1}{10}\) )
= \(\frac{3}{4}\) × \(\frac{8}{10}\)
= \(\frac{3 × 8}{4 × 10}\)
= \(\frac{24}{40}\)
= \(\frac{3}{5}\)
Hence,
\(\left(\frac{1}{10}+\frac{7}{10}\right)\) × \(\frac{3}{4}\) = \(\frac{3}{5}\)
Question 32.
\(\frac{4}{7}\) × \(\left(\frac{5}{8}-\frac{1}{4}\right)\) = _______
Answer:
\(\frac{4}{7}\) × \(\left(\frac{5}{8}-\frac{1}{4}\right)\) = \(\frac{3}{14}\)
Explanation:
The given fractions are: \(\frac{4}{7}\), \(\frac{5}{8}\) and \(\frac{1}{4}\)
So,
\(\frac{4}{7}\) × (\(\frac{5}{8}\) – \(\frac{1}{4}\) )
= \(\frac{4}{7}\) × (\(\frac{5 – 2}{8}\) )
= \(\frac{4}{7}\) × \(\frac{3}{8}\)
= \(\frac{3 × 4}{7 × 8}\)
= \(\frac{12}{56}\)
= \(\frac{3}{14}\)
Hence,
\(\frac{4}{7}\) × \(\left(\frac{5}{8}-\frac{1}{4}\right)\) = \(\frac{3}{14}\)
9.6 Find Areas of Rectangles
Use rectangles with unit fraction side lengths to find the area of the rectangle.
Question 33.
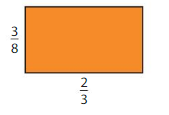
Answer:
The area of the rectangle is: \(\frac{1}{4}\)
Explanation:
The given figure is:
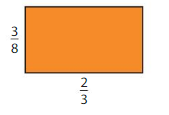
From the given figure,
The side lengths of the rectangle are: \(\frac{3}{8}\) and \(\frac{2}{3}\)
So,
The area of the rectangle = \(\frac{3}{8}\) × \(\frac{2}{3}\)
= \(\frac{2 × 3}{3 × 8}\)
= \(\frac{1}{4}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{1}{4}\)
Question 34.
Answer:
The area of the rectangle is: \(\frac{35}{48}\)
Explanation:
The given figure is:
From the given figure,
The side lengths of the rectangle are: \(\frac{7}{12}\) and \(\frac{5}{4}\)
So,
The area of the rectangle = \(\frac{7}{12}\) × \(\frac{5}{4}\)
= \(\frac{7 × 5}{12 × 4}\)
= \(\frac{35}{48}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{35}{48}\)
Question 35.
Find the area of a rectangle with side lengths of \(\frac{2}{9}\) and \(\frac{1}{10}\).
Answer:
The area of the rectangle is: \(\frac{1}{45}\)
Explanation:
The given side lengths of a rectangle are: \(\frac{2}{9}\) and \(\frac{1}{10}\)
So,
The area of the rectangle = \(\frac{2}{9}\) × \(\frac{1}{10}\)
= \(\frac{2 × 1}{10 × 9}\)
= \(\frac{1}{45}\)
Hence, from the above,
We can conclude that the area of the rectangle is: \(\frac{1}{45}\)
Question 36.
Find the area of a with a side length of \(\frac{3}{4}\).
Answer:
The area of the square is: \(\frac{9}{16}\)
Explanation:
The given side length of a square is: \(\frac{3}{4}\)
We know that,
The length of all sides of a square are equal
So,
the area of the square = \(\frac{3}{4}\) × \(\frac{3}{4}\)
= \(\frac{3 × 3}{4 × 4}\)
= \(\frac{9}{16}\)
Hence, from the above,
We can conclude that the area of the square is: \(\frac{9}{16}\)
9.7 Multiply Mixed Numbers
Multiply.
Question 37.
1\(\frac{1}{4}\) × 2\(\frac{1}{4}\) = _______
Answer:
1\(\frac{1}{4}\) × 2\(\frac{1}{4}\) =\(\frac{45}{16}\)
Explanation:
The given mixed fractions are: 1\(\frac{1}{4}\) and 2\(\frac{1}{4}\)
The representation of 1\(\frac{1}{4}\) and 2\(\frac{1}{4}\) in the improper fraction form is: \(\frac{5}{4}\) and \(\frac{9}{4}\)
So,
\(\frac{5}{4}\) × \(\frac{9}{4}\)
= \(\frac{5 × 9}{4 × 4}\)
= \(\frac{45}{16}\)
Hence,
1\(\frac{1}{4}\) × 2\(\frac{1}{4}\) =\(\frac{45}{16}\)
Question 38.
3\(\frac{4}{5}\) × 1\(\frac{1}{2}\) = _______
Answer:
3\(\frac{4}{5}\) × 1\(\frac{1}{2}\) = \(\frac{57}{10}\)
Explanation:
The given mixed fractions are: 3\(\frac{4}{5}\) and 1\(\frac{1}{2}\)
The representation of 3\(\frac{4}{5}\) and 1\(\frac{1}{2}\) in the improper fraction form is: \(\frac{19}{5}\) and \(\frac{3}{2}\)
So,
\(\frac{19}{5}\) × \(\frac{3}{2}\)
= \(\frac{19 × 3}{5 × 2}\)
= \(\frac{57}{10}\)
Hence,
3\(\frac{4}{5}\) × 1\(\frac{1}{2}\) = \(\frac{57}{10}\)
Question 39.
5\(\frac{1}{3}\) × 4\(\frac{7}{8}\) = _______
Answer:
5\(\frac{1}{3}\) × 4\(\frac{7}{8}\) = \(\frac{624}{24}\)
Explanation:
The given mixed fractions are: 5\(\frac{1}{3}\) and 4\(\frac{7}{8}\)
The representation of 5\(\frac{1}{3}\) and 4\(\frac{7}{8}\) in the improper fraction form is: \(\frac{16}{3}\) and \(\frac{39}{8}\)
So,
\(\frac{16}{3}\) × \(\frac{39}{8}\)
= \(\frac{39 × 16}{3 × 8}\)
= \(\frac{624}{24}\)
Hence,
5\(\frac{1}{3}\) × 4\(\frac{7}{8}\) = \(\frac{624}{24}\)
Question 40.
4\(\frac{5}{6}\) × 2\(\frac{9}{10}\) × \(\frac{1}{8}\) = _______
Answer:
4\(\frac{5}{6}\) × 2\(\frac{9}{10}\) × \(\frac{1}{8}\) = \(\frac{841}{480}\)
Explanation:
The given mixed fractions are: 4\(\frac{5}{6}\), 2\(\frac{9}{10}\) and \(\frac{1}{8}\)
The representation of 4\(\frac{5}{6}\) and 2\(\frac{9}{10}\) in the improper fraction form is: \(\frac{29}{6}\) and \(\frac{29}{10}\)
So,
\(\frac{29}{6}\) × \(\frac{29}{10}\) × \(\frac{1}{8}\)
= \(\frac{29 × 29 × 1}{8 × 10 × 6}\)
= \(\frac{841}{480}\)
Hence,
4\(\frac{5}{6}\) × 2\(\frac{9}{10}\) × \(\frac{1}{8}\) = \(\frac{841}{480}\)
Question 41.
Logic
Find the missing numbers.
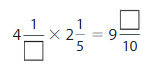
Answer:
The missing numbers are: 2 and 11
Explanation:
Let the missing numbers be: p and q
So,
4\(\frac{1}{p}\) × 2\(\frac{1}{5}\) = 9\(\frac{q}{10}\)
So,
To solve the mixed numbers, we can separate the whole numbers and the fraction numbers
So,
\(\frac{1}{p}\) × 2\(\frac{1}{5}\) = \(\frac{q}{10}\)
\(\frac{1}{p}\) × \(\frac{11}{5}\) = \(\frac{q}{10}\)
\(\frac{1 × 11}{p × 5}\) = \(\frac{q}{10}\)
\(\frac{11}{5p}\) = \(\frac{q}{10}\)
By comparing LHS and RHS
q = 11 and p = 2
Hence, from the above,
We can conclude that the missing numbers are: 2 and 11
9.8 Compare Factors and Products
Without calculating, tell whether the product is less than, greater than, or equal to each of its factors.
Question 42.
1\(\frac{1}{2}\) × 3
Answer:
The value of 1\(\frac{1}{2}\) × 3 is greater than 3
Explanation:
The given numbers are: 3 and 1\(\frac{1}{2}\)
The representation of 1\(\frac{1}{2}\) in the mixed form is: \(\frac{3}{2}\)
So,
\(\frac{3}{2}\) is greater than 1
So,
\(\frac{3}{2}\) × 3 is greater than 3
Hence, from the above,
We can conclude that the value of 1\(\frac{1}{2}\) × 3 is greater than 3
Question 43.
\(\frac{1}{8}\) × \(\frac{1}{6}\)
Answer:
The value of \(\frac{1}{8}\) × \(\frac{1}{6}\) is less than 1
Explanation:
The given numbers are: \(\frac{1}{8}\) and \(\frac{1}{6}\)
So,
\(\frac{1}{8}\) is less than 1
\(\frac{1}{6}\) is less than 1
So,
\(\frac{1}{8}\) × \(\frac{1}{6}\) is less than 1
Hence, from the above,
We can conclude that the value of \(\frac{1}{8}\) × \(\frac{1}{6}\) is less than 1
Question 44.
\(\frac{5}{5}\) × 2\(\frac{4}{7}\)
Answer:
The value of \(\frac{5}{5}\) × 2\(\frac{4}{7}\) is greater than 1
Explanation:
The given numbers are: \(\frac{5}{5}\) and 2\(\frac{4}{7}\)
The representation of 2\(\frac{4}{7}\) in the improper fraction form is: \(\frac{18}{7}\)
So,
\(\frac{18}{7}\) is greater than 1
\(\frac{5}{5}\) is 1
So,
\(\frac{5}{5}\) × 2\(\frac{4}{7}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{5}{5}\) × 2\(\frac{4}{7}\) is greater than 1
Question 45.
\(\frac{3}{4}\) × 2\(\frac{11}{12}\)
Answer:
The value of \(\frac{3}{4}\) × 2\(\frac{11}{12}\) is greater than 1
Explanation:
The given numbers are: \(\frac{3}{4}\) and 2\(\frac{11}{12}\)
The representation of 2\(\frac{11}{12}\) in the improper fraction form is: \(\frac{35}{12}\)
So,
\(\frac{35}{12}\) is greater than 1
\(\frac{3}{4}\) is less than 1
So,
\(\frac{3}{4}\) × 2\(\frac{11}{12}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{3}{4}\) × 2\(\frac{11}{12}\) is greater than 1
Question 46.
3\(\frac{1}{9}\) × 2\(\frac{7}{8}\)
Answer:
The value of 3\(\frac{1}{9}\) × 2\(\frac{7}{8}\) is greater than 1
Explanation:
The given mixed fractions are: 3\(\frac{1}{9}\) and 2\(\frac{7}{8}\)
The representation of 3\(\frac{1}{9}\) and 2\(\frac{7}{8}\) in the improper fractions form is: \(\frac{28}{9}\) and \(\frac{23}{8}\)
So,
\(\frac{28}{9}\) is greater than 1
\(\frac{23}{8}\) is greater than 1
So,
3\(\frac{1}{9}\) × 2\(\frac{7}{8}\) is greater than 1
Hence, from the above,
We can conclude that the value of 3\(\frac{1}{9}\) × 2\(\frac{7}{8}\) is greater than 1
Question 47.
\(\frac{9}{8}\) × \(\frac{5}{2}\)
Answer:
The value of \(\frac{9}{8}\) × \(\frac{5}{2}\) is greater than 1
Explanation:
The given fractions are: \(\frac{9}{8}\) and \(\frac{5}{2}\)
So,
\(\frac{9}{8}\) is greater than 1
So,
\(\frac{9}{8}\) × \(\frac{5}{2}\) is greater than 1
Hence, from the above,
We can conclude that the value of \(\frac{9}{8}\) × \(\frac{5}{2}\) is greater than 1
Conclusion:
Hope the information provided in the above answer key is beneficial for all the students of grade 5. Follow our Big Ideas Math Answers and make your learning fun and interesting.