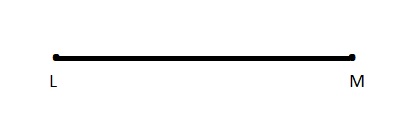Students who are looking for the BIM 4th Grade Answer Key Chapter 13 Identify and Draw Lines and Angles can get them on this page. We are here to give easy methods to solve the problems in Chapter 13 Identify and Draw Lines and Angles. Get the step by step explanation for all the question with examples here. Download Big Ideas Math Answers Grade 4 Chapter 13 Identify and Draw Lines and Angles pdf for free.
Big Ideas Math Book 4th Grade Answer Key Chapter 13 Identify and Draw Lines and Angles
Go through the topics covered in this chapter before starting your assignment. Identify and Draw Lines and Angles includes Points, Lines and Rays, Identify Parallel and Perpendicular Lines, Understand Degrees. If you want to learn Geometry it is necessary to learn deeply about angles and lines. Understand the concepts first and try to solve the problems given at the end of the chapter. Just click on the links and solve the problems.
Lesson: 1 Points, Lines and Rays
Lesson: 2 Identify and Draw Angles
Lesson: 3 Identify Parallel and Perpendicular Lines
- Lesson 13.3 Identify Parallel and Perpendicular Lines
- Identify Parallel and Perpendicular Lines Homework & Practice 13.3
Lesson: 4 Understand Degrees
Lesson: 5 Find Angle Measures
Lesson: 6 Measure and Draw Angles
Lesson: 7 Add Angle Measures
Lesson: 8 Find Unknown Angle Measures
Performance Task
- Identify and Draw Lines and Angles Performance Task 13
- Identify and Draw Lines and Angles Activity
- Identify and Draw Lines and Angles Chapter Practice 13
Lesson 13.1 Points, Lines and Rays
Explore and Grow
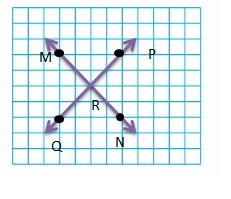
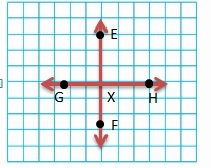
Use a straightedge to connect the dots A through Z. Describe the picture you make. How many points do you connect? How many line segments do you make?
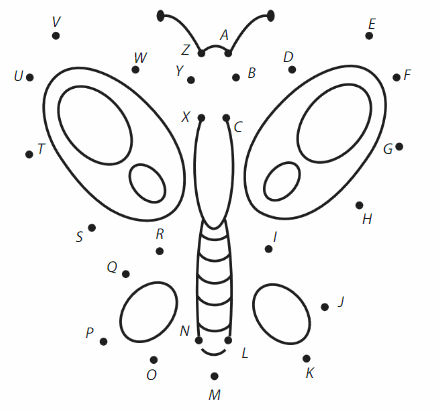
Answer:
Points connected are 25.
Line segments used are 25.
Structure
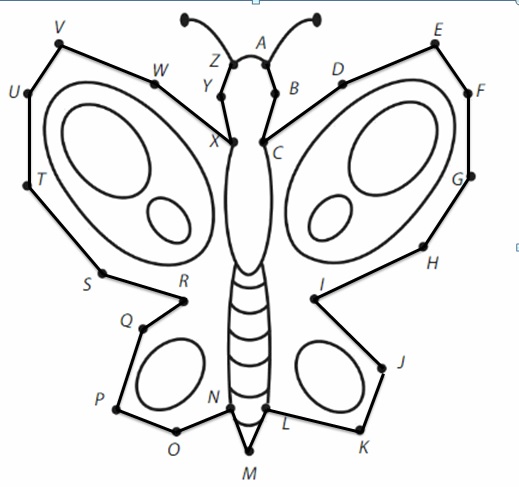
Draw your own connect-the-dots picture on another sheet of paper. Have your partner use a straightedge to connect the dots to make your picture. How many points did your partner connect? How many line segments did your partner make?
Answer:
Yes, he used line segments to connect the dots. He connected 20 dots and 19 line segments.

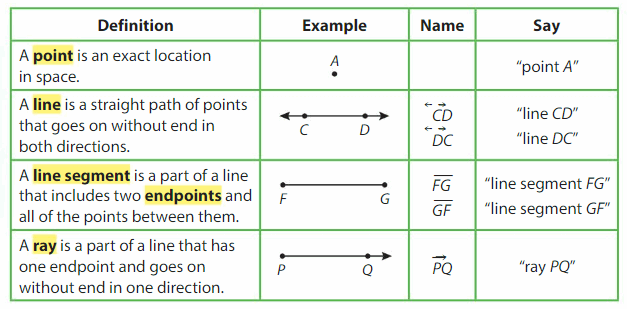
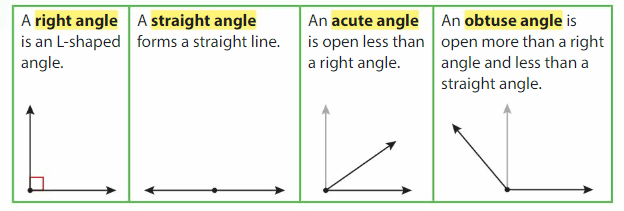
Think and Grow: Points, Lines, Line Segments, and Rays
Example
Draw and label \(\overline{L M}\)
\(\overline{L M}\) is a ___
Another name for \(\overline{L M}\) is ___
Answer:
Line segments are represented by a single overbar with no arrowheads over the letters representing the two endpoints.
The line segment Represented as \(\overline{L M}\)
Example
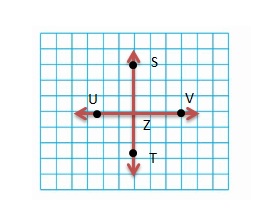
Draw and label \(\overrightarrow{S T}\)
\(\overrightarrow{S T}\) is a ___

Answer:
\(\overrightarrow{S T}\)
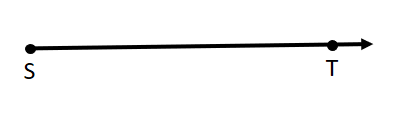
Ray \(\overrightarrow{S T}\)
Show and Grow
Question 1.
Name the figure shown. Write how to say the name.

Answer:
It is a line segment vu. Line segments are represented by a single overbar with no arrowheads over the letters representing the two endpoints.
It is represented as \(\overline{V U}\)
Question 2.
Draw and label two points P and Q on the line shown.

Answer:

Question 3.
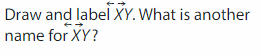
Answer:

Apply and Grow: Practice
Name the figure shown. Write how to say the name.
Question 4.
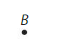
Answer:
It is called as point B.
A point in geometry is a location. It has no size i.e. no width, no length and no depth. A point is shown by a dot and named in capital letter.
Question 5.
Answer:
It is called as \(\overrightarrow{C D}\). The symbol of a ray is →.
Question 6.
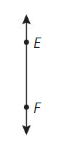
Draw and label the figure.
Answer:
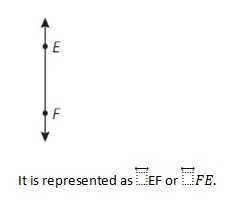
Question 7.
\(\overline{G H}\)
Answer:
\(\overline{G H}\) means a line segment. It is said as line segment GH.
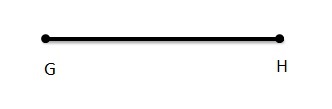
Question 8.
![]()
Answer:
It is a ray. It is said as ray![]()

Question 9.
\(\overrightarrow{L M}\)
Answer:
It means a ray. It is said as ray LM.
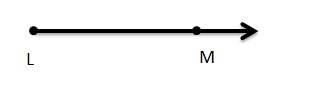
Use the figure.
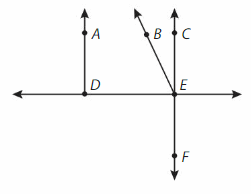
Question 10.
Name a ray.
Answer:
\(\overrightarrow{A D}\).
Question 11.
Name a point that lies on two lines.
Answer: E .
Question 12.
Name two different line segments.
Answer: DE and EF.
\(\overline{D E}\) and \(\overline{E F}\)
Question 13.
Logic
Your friend says he can draw two line segments between two points, and may be even more. His drawing is shown. Explain why this is not possible.
![]()
Answer:
Only one line can be drawn passing through any two points but a number of lines can be drawn through a point.
Think and Grow: Modeling Real Life
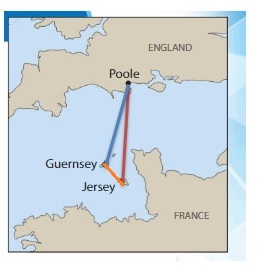
Example
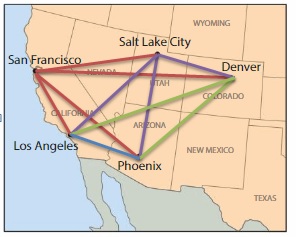
There are direct ferry routes between each pair of cities on the map. Draw line segments to represent all of the possible ferry routes. How many ferry routes did you draw in all?
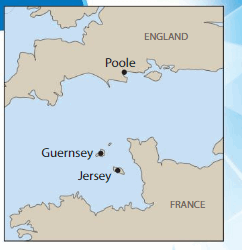
Start at Poole. Draw a line segment from Poole to each of the other cities. Repeat this process until a route is shown between each city.
You draw __ ferry routes in all.
Answer:
3 Possible routes.
Show and Grow
Question 14.
There are direct flights between each pair of cities on the map. Draw line segments to represent all of the possible flight routes. How many flights routes did you draw in all?
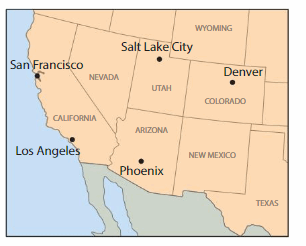
Answer:
Total 10 routes were found.
Question 15.
Which road signs contain a figure that looks like a ray?
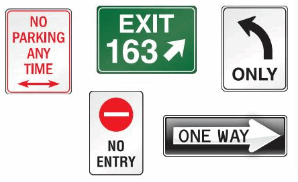
Answer:
One way road sign look like a ray.
Question 16.
Which letters in the banner can be made by drawing line segments? Explain.
 ,
,
Answer:
Letters – W,E,L,M AND E.
Points, Lines and Rays Homework & Practice 13.1
Name the figure shown. Write how to say the name.
Question 1.

Answer:
It is said as Line segment EF and represented as \(\overline{E F}\).
Question 2.

Answer:
It is said as ray GH and represented as \(\overrightarrow{G H}\).
Question 3.
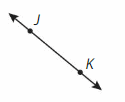
Answer:
It is said as line JK and represented as ![]()
Draw and label the figure.
Question 4.
two points L and M on the line shown
![]()
Answer:

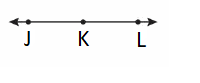
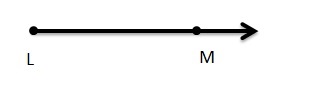
Question 5.
\(\overrightarrow{N O}\)
Answer:
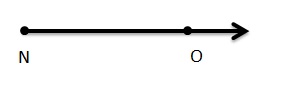
It is represented as \(\overrightarrow{N O}\).
Question 6.
![]()
Answer:

Use the figure.
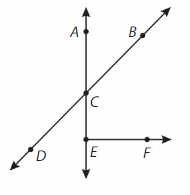
Question 7.
Name a line segment.
___CE____
Question 8.
Name two different rays.
Answer:
\(\overrightarrow{C D}\) and \(\overrightarrow{E F}\).
Question 9.
Name two different lines
Answer
\(\overline{D B}\)and \(\overline{A E}\).
Question 10.
Writing
Explain the difference between a line and a line segment.
Line-segment
1. It has two end points.
2. The length of a line-segment is definite. So, it can be measured.
3. The symbol of a line-segment is _____
Line
1. There are no end points in a line.
2. There are no end points. So, length of a line cannot be measured.
3. The symbol of a line is ↔
Question 11.
Structure
Name the figure in as many ways as possible.
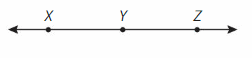
Answer:
\(\overline{X Y}\),\(\overline{Y Z}\) and \(\overline{X Z}\).
\(\overrightarrow{Y Z }\)
LINE – XZ
Question 12.
Structure
Draw and label a figure that has four points, two rays, and one line segment.
Answer:
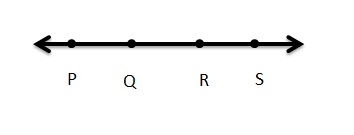
\(\overrightarrow{R S }\) and \(\overrightarrow{Q S}\).
\(\overline{P S}\)
DIG DEEPER!
Write whether the statement is true or false. If false, explain.
Question 13.
A line segment is part of a line. _______
Answer: Yes
Question 14.
A ray is part of a line segment. ____
Answer:
No
Explanation:
Line-segment- It has two end points. But where as Ray has a starting point but no other end point.
Question 15.
There are an infinite number of points on a line. ___
Answer: Yes
Question 16.
Modeling Real Life
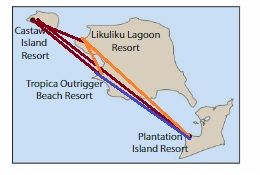
There are direct helicopter flights between each pair of resorts on the map. Draw line segments to represent all of the possible flight routes. How many flight routes did you draw in all?
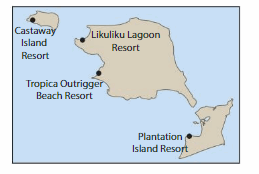
Answer:
Total possible flight routes are 6 routes.
Question 17.
Modeling Real Life
Which road signs contain a figure that looks like it is made of only line segments?

Answer:
Road signs – +,T and Y are made of line segments.
Review & Refresh
Compare
Question 18.
![]()
Answer:
0.15 < 0.16.
Question 19.
![]()
Answer:
2.4 < 2.42
Question 20.
![]()
Answer:
6.90 = 6.9
Lesson 13.2 Identify and Draw Angles
Explore and Grow
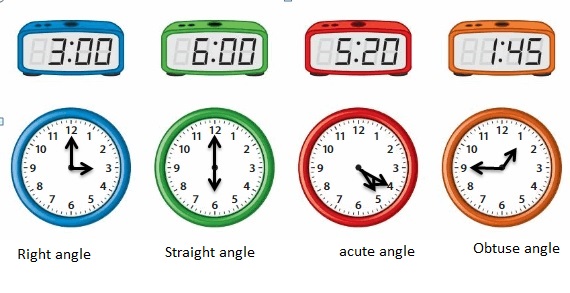
Draw the hands of the clock to represent the given time.

For each clock, describe the angle that is formed by the minute hand and the hour hand.
Answer:
Reasoning
Explain how line segments, rays, and angles can be related.
Think and Grow: Angles
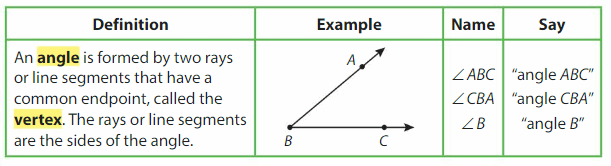
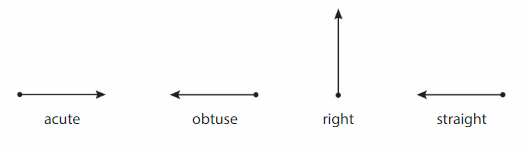
Angles can be either right, straight, acute, or obtuse.
Example
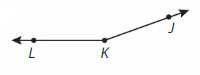
Write three names for the angle and classify it.
Three names for the angle are
___, ____ and ____.
The angle opens ___ a right angle and less than a straight line.
So, it is an __ angle.
Answer:
Three names for the angle are actue, obtuse and right angles.
The angle opens more than a right angle and less than a straight line.
So, it is an obtuse angle.
Show and Grow
write a name for the angle and classify it.
Question 1.
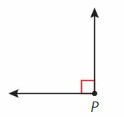
Answer:
It is a right angle called as ∠P.
Question 2.
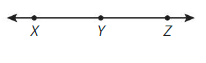
Answer:
It is a straight angle. It can be represented as ∠XYZ, ∠ZYX.
Apply and Grow: Practice
Write a name for the angle and classify it.
Question 4.
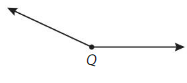
Answer:
It is a obtuse angle. It is represented as ∠Q.
Question 5.
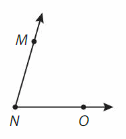
Answer:
It is a actue angle. It is represented as ∠MNO or ∠ONM.
Question 6.
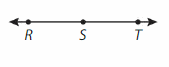
Answer:
It is a straight angle. It can be represented as ∠RST, ∠TSR.
Draw and label the angle.
Question 7.
∠XYZ is right
Question 8.
∠JKL is straight.
Answer:
Use the figure. Use three letters to name each angle.
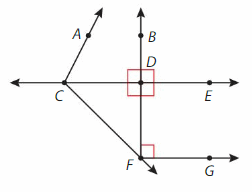
Question 9.
Name an acute angle.
Answer:
∠CFD
Question 10.
Name two different obtuse angles.
Answer:
∠CFG and ∠ACF.
Question 11.
Name two different straight angles.
Answer:
∠BDF and ∠CDE.
Question 12.
Name three different right angles.
Answer:
∠CFD , ∠CFG and ∠BDF.
Question 13.
Structure
Draw to complete each angle.
Answer:
Think and Grow: Modeling Real Life
Example
Which angle of the skateboard ramp is acute?
You need to find an angle that is open less than a right angle.

Angle A opens __more than __ a right angle and less than a straight line.
Angle B _is equal__ a right angle.
Angle C opens _less than__ a right angle.
Angle _∠C__ is an acute angle.
Show and Grow
Question 14.
Use three letters to name an angle of the wind turbine that is obtuse.
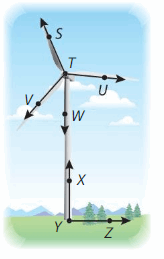
Answer:
∠VTU.
Question 15.
Trace and label two right angles, two obtuse angles, and two acute angles in the painting.

Answer:
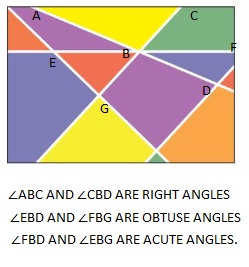
Question 16.
DIG DEEPER!
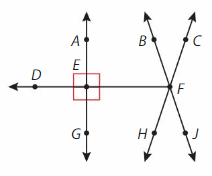
How many different angles are in the window? Name all of the different angles.
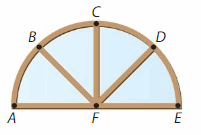
Answer:
Right angles – ∠AFC , ∠BFD , ∠CFE
Obtuse angles – ∠AFD and ∠BFE.
Acute angles – ∠AFB, ∠BFC , ∠CFD and ∠DFE.
Straight angles – ∠AFE.
Identify and Draw Angles Homework & Practice 13.2
Write a name for the angle and classify it.
Question 1.
![]()
Answer:
∠O is straight angle.
Question 2.
Answer:
∠TUV is a right angle as TU is perpendicular to UV .
Question 3.
 ∠
∠
Answer:
∠XYZ is a obtuse angle as, we can see clearly angle formed is more than 90 degrees.
Draw and label the angle.
Question 4.
∠ABC is obtuse.
Answer:
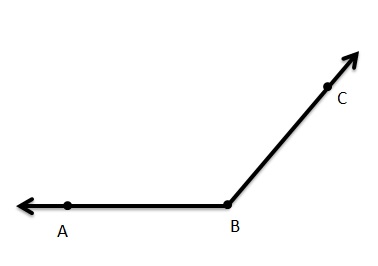
Question 5.
∠MNO is acute.
Answer:
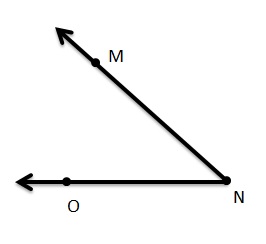
Use the figure. Use three letters to name each angle.
Question 6.
Name an acute angle.
Answer: ∠BFC
Question 7.
Name a straight angle.
Answer: ∠DEF
Question 8.
Name two different right angles.
Answer: ∠DEA and ∠DEG.
Question 9.
Name three different obtuse angles
Answer: ∠EFJ and ∠EFC.
Question 10.
YOU BE THE TEACHER
Answer:
The above figure contains ∠JKL a angle.
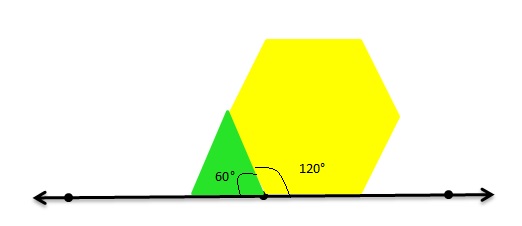
Question 11.
DIG DEEPER!
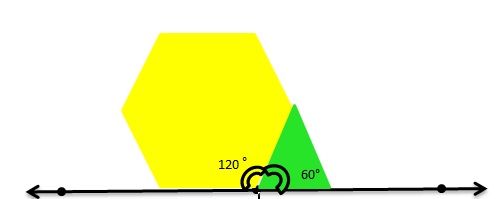
Can you make a straight angle using an acute angle and an obtuse angle that share a common ray? Draw a picture to support your answer.
Answer:
Yes
Explanation:
The total sum of a straight angle =180.
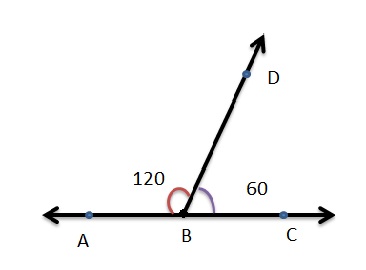
As per the figure,
The Obtuse angle = 120 degrees.
The acute angle = 60 degrees.
Therefore The straight angle = Obtuse angle + Acute angle.
= 120 + 60
= 180 degrees.
Question 12.
Structure
Write a capital letter that has more than two right angles.
Answer: B
Question 13.
Modeling Real Life
Use three letters to name the angles of the flag of the Czech Republic that are obtuse.

Answer:
∠AFC and ∠EFC are obtuse angles.
Question 14.
Modeling Real Life
Horses see an object with binocular both eyes at the same time using vision. Classify the angle that describes the horse’s binocular vision.
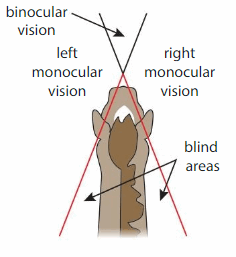
Answer:
The angle that formed in binocular vision is Acute angle.
Review & Refresh
Question 15.
Write 1\(\frac{7}{12}\) as a fraction.
Answer:
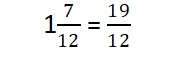
(1 x 12 ) + 7 =19
Question 16.
Write \(\frac{9}{6}\) as a mixed number.
Answer:

Lesson 13.3 Identify Parallel and Perpendicular Lines
Explore and Grow
Use a straightedge to draw and label a figure for each description. If a figure cannot be drawn, explain why.

Answer:
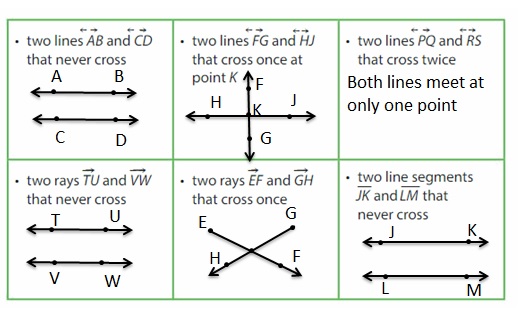
Reasoning
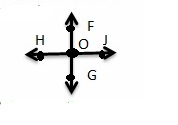
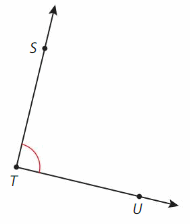
Find the figure that shows two lines that cross once. How many angles are formed by two lines? Name and classify the angles of the figure above.
Answer:
Four angles are formed – ∠FOJ , ∠FOH ,∠GOJ and ∠GOH.
Think and Grow: Parallel and Perpendicular Lines
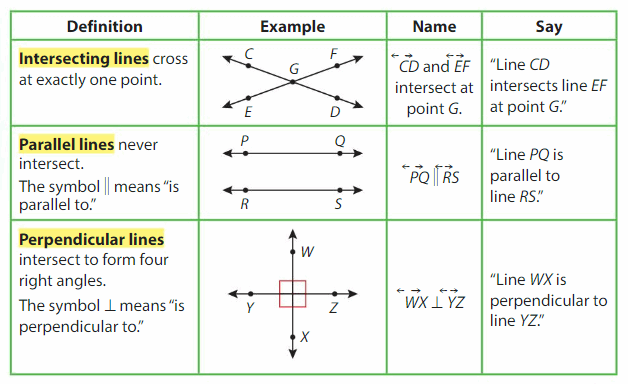
You can describe a pair of lines as intersecting, parallel, or perpendicular.
Example
Draw and label the lines with the given description.


Answer:
Show and Grow
Draw and label the lines with the given description.
Question 1.
Answer:
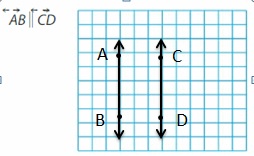
Question 2.
Answer:
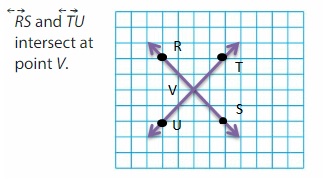
Apply and Grow: Practice
Draw and label the lines with the given description.
Question 3.
Answer:
Question 4.
Answer:
Use the figure.
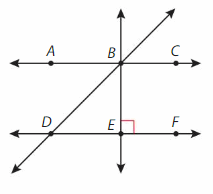
Question 5.
Name a pair of lines that appear to be parallel.
Answer:
AC ll DF.
Question 6.
Name two lines that are perpendicular.
Answer:
BE ⊥ DF and DE ⊥ EB.
Question 7.
Name two intersecting lines.
Answer:
DE and EB
CB and BE
Question 8.
Reasoning
All perpendicular lines are also intersecting lines. Are all intersecting lines perpendicular? Explain.
Answer:
Perpendicular Lines means which bisect the lines at right angles .But where as the intersecting lines meet at one point but doesnot form right angles.
Question 9.
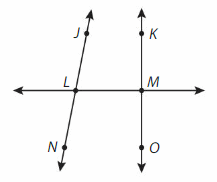
Think and Grow: Modeling Real Life
Example
Which street appears to be parallel to 2nd Street?
Look for a street that will not intersect with 2nd street.
___ Street appears to be parallel to 2nd Street.
Answer:
3rd street.
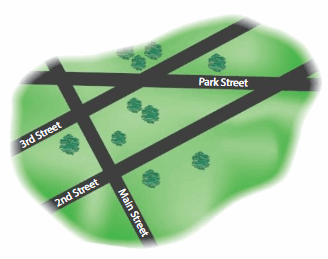
Show and Grow
Question 10.
Which trail appears to be parallel to Fox Trail?
Answer:
Wolf Run Trail
Question 11.
Which trail appears to be perpendicular to Fox Trail?
Answer:
Oak Trail.
Question 12.
Trace and label a pair of line segments that appear to be parallel and a pair of line segments that appear to be perpendicular.
Answer:
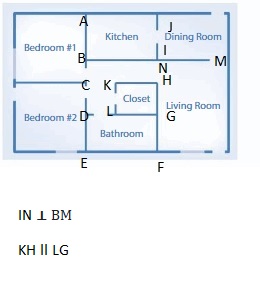
Question 13.
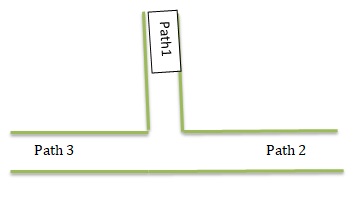
DIG DEEPER!
Design three paths for a park. Two of the paths are perpendicular. Label these paths as Path 1 and Path 2. The third path intersects both perpendicular paths at exactly one point. Label this path as Path 3.
Answer:
Identify Parallel and Perpendicular Lines Homework & Practice 13.3
Example
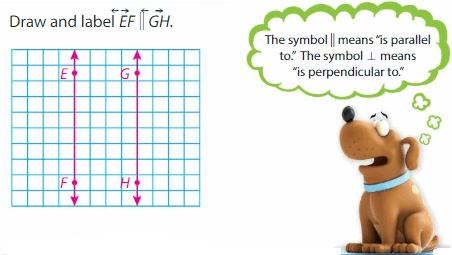
Draw and label the lines with the given description.
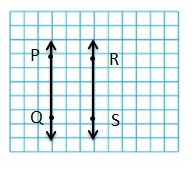
Question 1.
Answer:
Question 2.

Answer:
Use the figure.
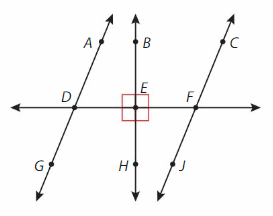
Question 3.
Name a pair of lines that appear to be parallel.
Answer:
AG ll CJ
Question 4.
Name two lines that are perpendicular.
Answer:
BE ⊥ DF
HE ⊥ DF
Question 5.
Name two intersecting lines.
Answer:
CJ and DF .
Question 6.
Structure
Name two line segments that appear to be parallel. Then name two line segments that appear to be perpendicular.
Answer:
AB ll DC and AD⊥ DC .
Question 7.
Reasoning
Can two lines that share a point be parallel? Explain.
Answer:
Two Lines can be parallel but a point cannot be a parallel.
Explanation:
Parallel lines are co planar lines that do not intersect. In two dimensions, parallel lines have the same slope . We can write the equation of a line parallel to a given line if we know a point on the line and an equation of the given line. y=2x+3 .
Question 8.
DIG DEEPER!
 l
l
Answer:
No, It cannot be an acute angle. Because it is a right angle.
Explanation:
As line SW is perpendicular to line UV and line SW is parallel to line TX then from figure it is clear that line TX will be perpendicular to line UV.
Question 9.
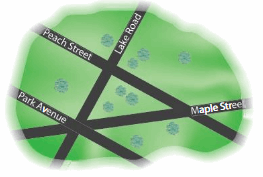
Modeling Real Life
Which street appears to be parallel to Park Avenue?
Answer:
Peach Street.
Question 10.
Modeling Real Life
Which street appears to be perpendicular to Peach Street?
Answer:
Lake Road
Question 11.
Modeling Real Life
Trace and label a pair of line segments that appear to be parallel and a pair of line segments that appear to be perpendicular.
Answer:
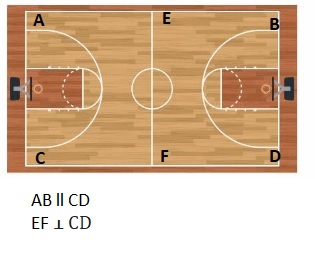
Review & Refresh
Find the equivalent amount of time.
Question 12.
20 min = ___ sec
Answer:
1min = 60sec
20 mins = 20 x 60
= 1200 sec.
Question 13.
6 yr = ___ wk
Answer:
1 year = 52 weeks.
6 years = 6 x 52
= 312 weeks
Lesson 13.4 Understand Degrees
Explore and Grow
Find the elapsed time for each set of clocks. Describe, in your own words, the turn that the minute hand makes.

Answer:
Elapsed time is the time or difference between a beginning time and an ending time.
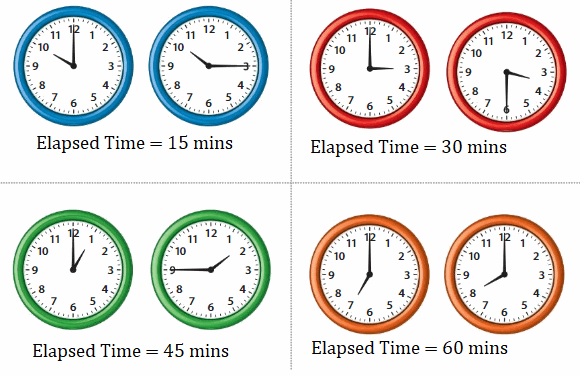
Reasoning
Explain how elapsed time shown by an analog clock relates to angles formed in a circle.
Answer:
On a clock, we can see different kinds of angles based on its amplitude; void, acute, straight, obtuse, flat angles—even a full angle.
Think and Grow: Degrees
Angles are measured in units called degrees. Think of dividing a circle into 360 equal parts. An angle that turns through \(\frac{1}{360}\) of a circle measures 1°, and is called a“one-degree angle.” A full turn through the entire circle is 360°.

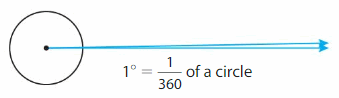
Example
Find the measure of the angle.
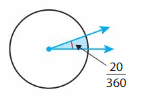
An angle that turns \(\frac{1}{360}\) of a circle measures _1__ degrees.
An angle that turns through \(\frac{20}{360}\) of a circle measures _20__ degrees.
So, the measure of the angle is _20 degrees__.
Example
Find the measure of a right angle.
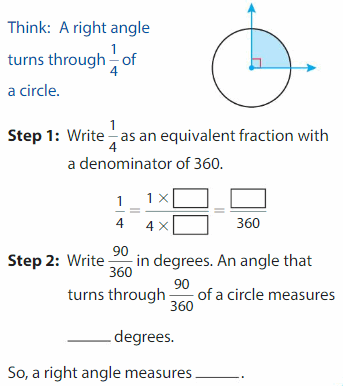
Answer:
22.5 degrees.
Show and Grow
Find the measure of the angle.
Question 1.
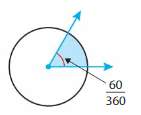
Answer:
60 degrees.
Question 2.
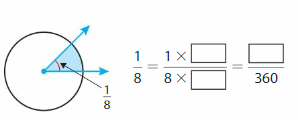
Answer:
45 degrees.
Apply and Grow: Practice
Find the measure of the angle.
Question 3.
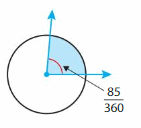
Answer:
85 degrees
Question 4.
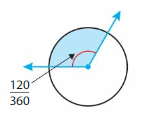
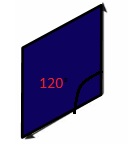
Answer:
120 degrees.
Question 5.
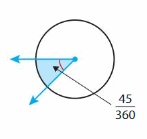
Answer:
45 degrees.
Question 6.
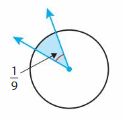
Answer:
(1/9) x (—/—) = —–/360
=40 degrees.
Question 7.
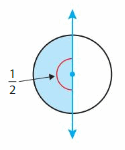
Answer:
(1/2) x (—/—) = —–/360
=180 degrees.
Question 8.
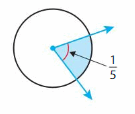
Answer:
(1/5) x (—/—) = —–/360
=360/5=72 degrees.
Question 9.
A circle is divided into 8 equal parts. What is the measure of the angle that turns through 2 parts?
Answer:
Number of parts =8
Total sum of angle in circle = 360.
Measure of 1/8 part of angle formed = 360/8 =45 degree.
Therefore measure of angle that turns through 2 parts = 2 x 45 =90 degrees.
Question 10.
A circle is divided into 4 equal parts. What is the measure of the angle that turns through 3 parts?
Answer:
Number of parts =4
Total sum of angle in circle = 360.
Measure of 1/4 part of angle formed = 360/4 =90 degree.
Therefore measure of angle that turns through 3 parts = 3 x 45 =135 degrees.
Classify the angle as right, straight, acute or obtuse.
Question 11.
30°
Answer:
Acute angle
An acute angle lies between 0 degree and 90 degrees, or in other words; an acute angle is one that is less than 90 degrees.
Question 12.
120°
Answer:
Obtuse angle
It is the angle which lies between 90 degrees and 180 degrees or in other words; an obtuse angle is greater than 90 degrees and less than 180 degrees.
Question 13.
90°
Answer:
Right angle
A right angle is always equal to 90 degrees.
Question 14.
180°
Answer:
Straight angle
A straight angle is 180 degrees. It is just a straight angle because the angle between its arms is 180 degrees.
Reflex Angle
Question 15.
YOU BE THE TEACHER
Both circles are divided into sixths. Your friend says the measure of Angle D is greater than the measure of Angle C. Is your friend correct? Explain.
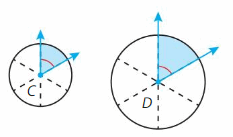
Answer:
No
Explanation:
Both the angles are divided into 6 equal parts irrespective of size of the circle. Both the angles C and D will be equal. As the sum of the circles is 360 degrees for all circles ,when divided equally the angles will be equal.
Question 16.
Reasoning
Does each figure show the same angle? If not, which two angles are shown? Explain your reasoning.
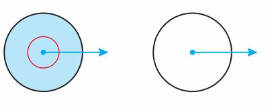
Answer:
Both the Angles are equal.
Think and Grow: Modeling Real Life
Example
Spokes divide the Ferris wheel into 20 equal parts. What is the angle measure of 1 part?
Write a fraction that represents 1 part.
Because the Ferris wheel has 20 equal parts,

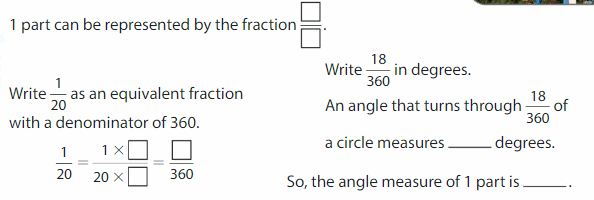
Answer:

Show and Grow
Question 17.
The game spinner is divided into10 equal parts. What is the angle measure of 1 part?

Answer:
Number of parts divided=10
Total sum of angle in circle = 360.
Measure of 1/10 part of angle formed = 360/10 =36 degree.
Question 18.
DIG DEEPER!
A circular quesadilla is cut into 8 equal pieces. Five pieces are eaten. What is the angle measure formed by the remaining pieces?
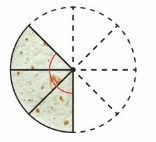
Answer:
Total Number of parts divided = 8.
Total sum of angle = 360 degrees.
Angle of each part = 360/8 degrees = 45 degrees.
Number of parts eaten = 5
Angle of 5 parts = 5 x 45 degrees = 225 degrees.
Angle formed by remaining parts = 360- 225 degrees =135 degrees
or
Number of remaining parts =3
Angle of remaining parts = 3 x 45 degrees. = 135 degrees.
Question 19.
DIG DEEPER!
When a light wave hits an object, the object reflects a colored light at an angle to your eye. The color of the reflected light is the color you see. What fraction of a circle is shown by the angle? Explain.
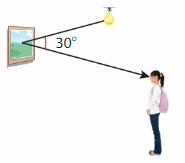
Answer:
Reflected angle = 30 degrees.
Total sum of angle = 360 degrees.
Fraction angle reflected in circle = 30 / 360 degrees = 1 /12 fraction.
Understand Degrees Homework & Practice 13.4
Find the measure of each angle
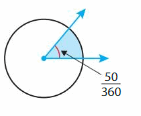
Question 1.
Answer:
50 degrees
Question 2.
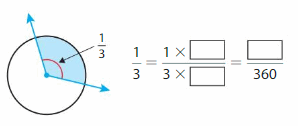
Answer:
(1/3) x (—/—) = —–/360
= 360/3 = 120 degrees.
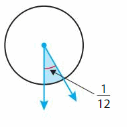
Question 3.
Answer:
(1/12) x (—/—) = —–/360
= 360/12 = 30 degrees.
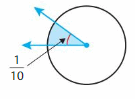
Question 4.
Answer:
(1/10) x (—/—) = —–/360
=360/10 = 36 degrees.
Question 5.
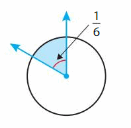
Answer:
(1/6) x (—/—) = —–/360
= 360/6 = 60 degrees.
Question 6.
A circle is divided into 5 equal parts. What is the measure of the angle that turns through 2 parts?
Answer:
Number of parts =5
Total sum of angle in circle = 360.
Measure of 1/5 part of angle formed = 360/5 =72 degree.
Therefore measure of angle that turns through 2 parts = 2 x 72 =144 degrees.
Question 7.
A circle is divided into 10 equal parts. What is the measure of the angle that turns through 3 parts?
Answer:
Number of parts =10
Total sum of angle in circle = 360.
Measure of 1/10 part of angle formed = 360/10 =36 degree.
Therefore measure of angle that turns through 3 parts = 3 x 36 =108 degrees.
Classify the angle as right, straight, acute, obtuse
Question 8.
90°
Answer:
Right angle
A right angle is always equal to 90 degrees.
Question 9.
45°
Answer:
Acute angle
An acute angle lies between 0 degree and 90 degrees, or in other words; an acute angle is one that is less than 90 degrees.
Question 10.
160°
Answer:
Obtuse angle
It is the angle which lies between 90 degrees and 180 degrees or in other words; an obtuse angle is greater than 90 degrees and less than 180 degrees.
Question 11.
60°
Answer:
Acute angle
An acute angle lies between 0 degree and 90 degrees, or in other words; an acute angle is one that is less than 90 degrees.
Question 12.
Which One Doesn’t Belong? Which angle measure does not belong with the other three?
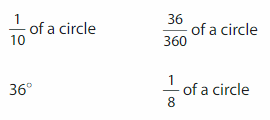
Answer:
1/8 of a circle
Question 13.
DIG DEEPER!
Your friend uses the equation to find an angle a measure. Explain what the letters a and b represent.
360° ÷ a = b
Answer:
Where a is the Number of parts where circle is divided.
b is the angle of 1 part.
Question 14.
Modeling Real Life
The steering wheel is divided into 3 equal parts. Find the angle measure of 1 part.

Answer:
Number of parts =3
The total sum of angle in circle = 360.
The measure of 1/3 part of the angle formed = 360/3 =120 degrees.
Question 15.
DIG DEEPER!
You and your friend take pie-shaped pieces from a circular quiche. Your friend takes \(\frac{2}{8}\) of the quiche. You take a piece with an angle measure of 72°. Who takes a larger piece? Explain.
Answer:
It Is given that pie taken your friend is 2/8 So it is clear that quinche is divided into 8 parts.
Number of parts =8
Total sum of angle in circle = 360.
Measure of 1/8 part of angle formed = 360/8 =45 degree.
Piece taken by friend is 2/8 = 2 x 45 = 90 degrees.
Piece taken by you measures 72 degrees.
Therefore Your Friend takes larger piece.
Review & Refresh
Multiply
Question 16.
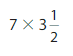
Answer:
=7 x (7/2)
=1/2 = 0.5
Question 17.
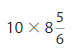
Answer:
= 10 x (53/6)
=88.33
Question 18.
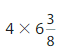
Answer:
=4 x (51/8)
=51/2
=25.5
Lesson 13.5 Find Angle Measures
Explore and Grow
How many triangular pattern blocks can you put together around one vertex?
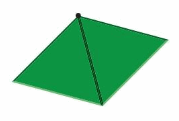
Answer: 2
How can you determine the measure of each angle in a triangular pattern block?
Answer:
If we add all three angles in any triangle we get 180 degrees.
So, the measure of (angle A + angle B + angle C) = 180 degrees.
Repeated Reasoning
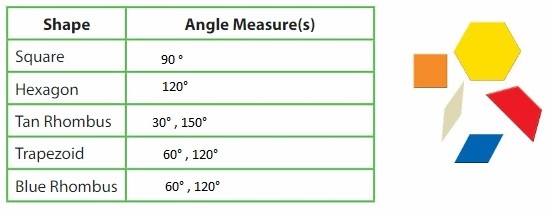
Find all of the angle measures of the other pattern blocks. Organize your results in the table.

Answer:
Think and Grow: Find Angle Measures
Example
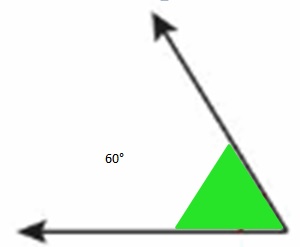
Use the pattern block to find the measure of the angle.
Each angle of the pattern block has a measure of _60__.
The angle is equal to _60 degrees__ of the angles of the pattern block.
So, the measure of the angle is __60 degrees_.
Example
Use the pattern block to find the measure of the angle.
Each acute angle of the pattern block has a measure of _30__.
The angle is equal to _30__ of the acute angles of the pattern block.
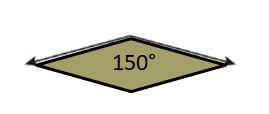
So, the measure of the angle is _150 degrees__.
Show and Grow
Use pattern blocks to find the measure of the angle.
Question 1.
Answer:
Question 2.
Answer:
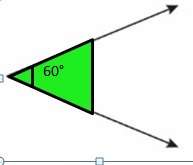
Question 3.
Use pattern blocks to find how many 60° angles are in a straight angle.

Answer:
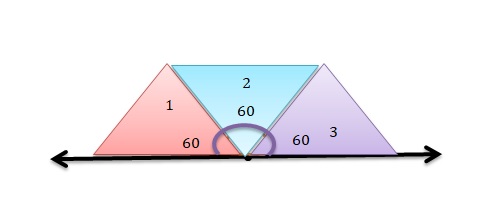
Total 3 triangles are used.
Apply and Grow: Practice
Use pattern blocks to find the measure of the angle.
Question 4.

Answer:
Question 5.
Answer:
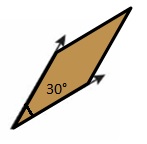
Question 6.

Answer:
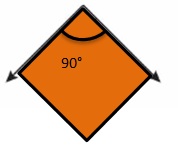
Question 7.
Answer:
Question 8.
Answer:
Question 9.
Answer:
Question 10.
How many 90° angles are in a straight angle? Explain.
Answer: 2
A straight has 180 degree as its sum of angle.
One right angle = 90 degrees.
=90 x2 =180.
So if we have 2 right angles the its sum will be equal to 180 degrees.
Question 11.
How many 30° angles are in a 150° angle? Explain.
Answer:
=150/30=5 times.
Question 12.
Structure
Use two different pattern blocks to form an obtuse angle. Find the angle measure. Draw a model to support your Answer.
Question 13.
DIG DEEPER!
Find the measure of the smaller angle formed by the clock hands. Then explain how you could find the measure of the larger angle.

Answer:
The angle formed at 3 clock = 90°.
The sum of angles=360°
The larger angle = 360° – 90°=270°
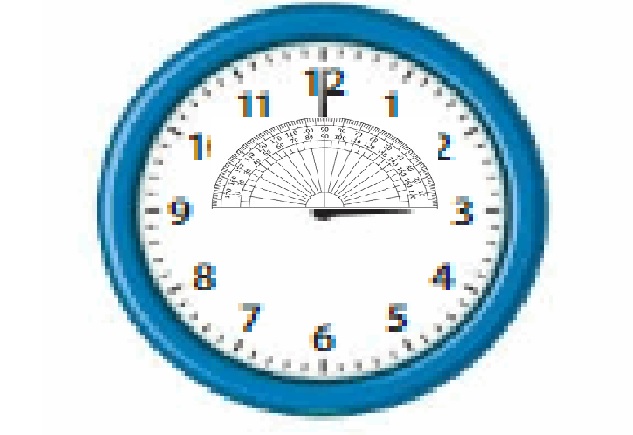
Think and Grow: Modeling Real Life
Example
A circular compass is divided into 8 equal sections. What is the measure of each angle formed at the center of the compass?

A full turn through a circle is 360°. So, divide 360° by 8.

Each angle formed at the center of the compass is __45°_.
Show and Grow
Question 14.
You have a circular craft table. You divide the table into 3 equal sections. What is the measure of each angle formed at the center of the table?
Answer:
Number of sections =3
The total sum of angle in circle = 360°.
The measure of 1/3 part of the angle formed at the center of the table = 360°/3 =120°
Question 15.
A chef has a wheel of cheese that is cut into6 equal pieces. The chef uses 2 pieces. What is the angle measure formed by the missing pieces?
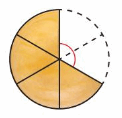
Answer:
Number of parts =6
Total sum of angle in circle = 360°.
Measure of 1/6 part of angle formed= 360°/6 =60°
Chef uses 2 peices
Angle formed by used peices = 2 x 60° =120°
Therefore, the angle measure formed by the missing pieces = 120°
Question 16.What is the angle measure formed by the remaining slices?
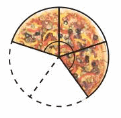
Answer:
Number of parts =5
Total sum of angle in circle = 360°.
Measure of 1/5 part of angle formed= 360°/5 =72°
used peices = 2
Angle formed by Remaining peices = 3 x 72° =216°
Therefore, the angle measure formed by the remaining pieces = 216°
Question 17.
DIG DEEPER!
You make a tile pattern for a border on a wall. Each tile is the same size and shape as a pattern block. Draw two ways you can arrange 1 triangle tile and 1 hexagon tile to create a straight angle.
Answer:
Find Angle Measures Homework & Practice 13.5
Use pattern blocks to find the measure of the angle.
Question 1.
Answer:
Question 2.

Answer:
Question 3.

Answer:

Question 4.
Answer:
Question 5.
Answer:
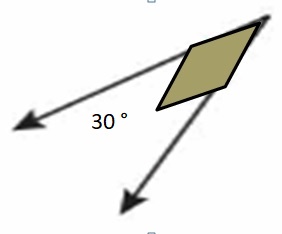
Question 6.
Answer: The angle formed is 80°. It cannot be represented by pattern blocks.
Question 7.
How many 30° angles are in a right angle? Explain.
Answer:
Right angle =90°
How many 30° angles we have in right angle = 90°/30°=3
Question 8.
Structure
Draw to show how you can use three different pattern blocks to form a straight angle.
Answer:
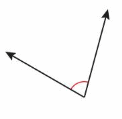
Question 9.
YOU BE THE TEACHER
Your friend says the measure of the angle shown is 120°. Is your friend correct? Explain.

Answer: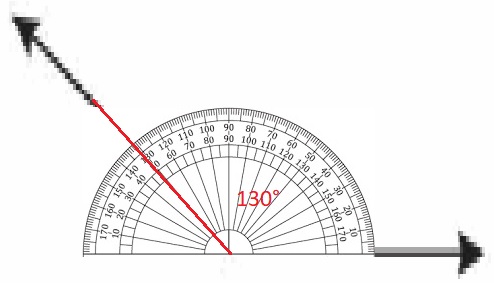
No, As the angle is 130°.
Question 10.
DIG DEEPER!
The hands of a clock form a straight angle. What time could it be? Explain.
Answer:
The time as per mage is 6 o clock.
Explanation:
- One hand is very thin and moves very fast. It’s called the seconds hand. Every time it moves, a second has gone by.
- Another hand is thick and long like the seconds hand. It’s called the minutes hand. Every time it moves one little tick, a minute has gone by. Every 60 times it moves a whole step, an hour has gone by.
- The last hand is thick, too, but smaller than the minutes hand. It’s called the hours hand. Every time it moves one big tick, an hour has gone by. Every 24 times it moves a whole step, a day has gone by
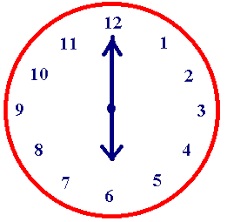
Question 11.
Modeling Real Life
The scale is divided into 5 equal sections by each whole kilogram measurement. What is the measure of each angle formed at the center of the scale? What is the mass of the bananas?

Answer:
The whole Kilogram is divided into 5 parts
1kg = 1000 grams
=1000 grams / 5
=200 grams.
As per the image the weight of banans showing mark on one.
one unit = 200 grams.
Therefor, weight of bananas = 200 grams.
Question 12.
DIG DEEPER!
The gasoline tank gauge is divided into 4 equal sections. What are the measures of the angles formed at the starting point of the red arrow?
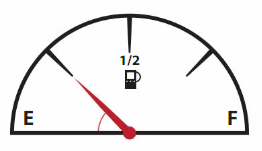
Answer:
The gasoline is in a shape of semi circle.
Sum of the angles = 180°
Number of sections divided = 4 parts. (equal).
Angle of each section : 180° /4 = 45° .
Therefore the measures of the angles formed at the starting point of the red arrow = 45° .
Review & Refresh
Find the area of the rectangle.
Question 13.
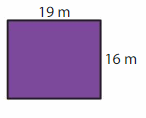
Answer:
Area of Rectangle = length X breadth.
AREA = 19 m x 16 m = 304 sq m.
Question 14.
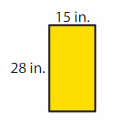
Answer:
Area of Rectangle = length X breadth.
AREA = 28 in x 15 in =420 sq in.
Lesson 13.6 Measure and Draw Angles
Explore and Grow
Find the measure of each angle. Then classify it.
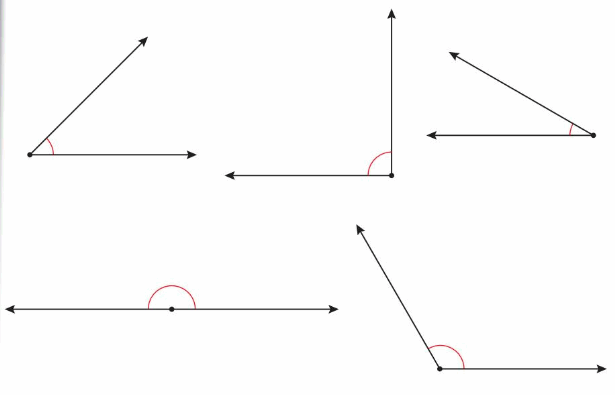
Answer:
Construct Arguments
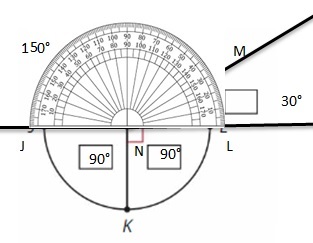
Does the angle shown have a measure of 90°? Explain.
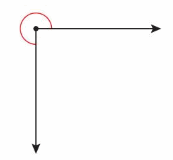
Answer:
The intersecting line form right angle =90 degrees
The angle marked = ?
The total angle = 360 degrees.
The marked angle= 360 – 90 = 270 degrees.
Think and Grow: Measure and Draw Angles
Example
A protractor is a tool for measuring and drawing angles.
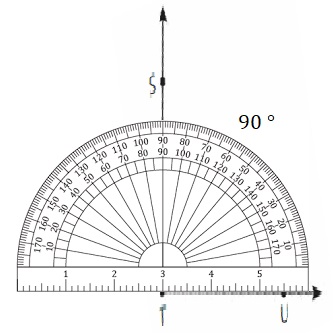
Find the measure of ∠STU. Then classify it.
Step 1: Place the center of the protractor on the vertex of the angle.
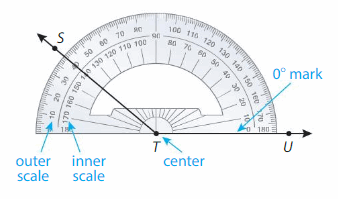
Step 2: Align one side of the angle, \(\overrightarrow{T U}\), with 0° mark on the inner scale of the protractor.
Step 3: Find where the other side of the angle, \(\overrightarrow{T S}\), passes through the inner scale.
So, the measure of ∠STU is ___. It is an ___ angle.
Example
Draw ∠ABC that measures 65°.
Step 1: Place the center of the protractor on point. Align \(\overrightarrow{B C}\) with the 0° mark on the inner scale of the protractor.
Step 2: Use the same scale to draw a point at 65°. Label the point A.
Step 3: Use the protractor to draw \(\overrightarrow{B A}\).
Answer:

Show and Grow
Question 1.
Find the measure of ∠DEF. Then classify it.
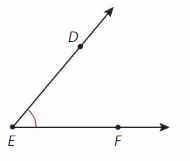
Answer:
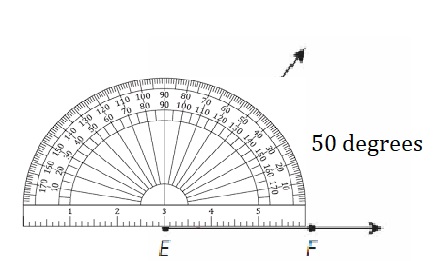
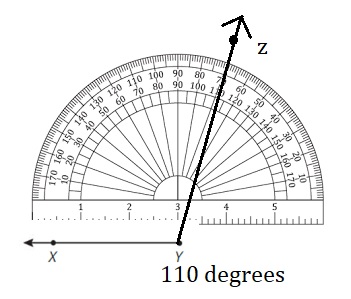
Question 2.
Use a protractor to draw ∠XYZ that measures 110°.

Answer:
Apply and Grow: Practice
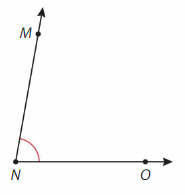
Find the measure of the angle. Then classify it.
Question 3.
Answer:
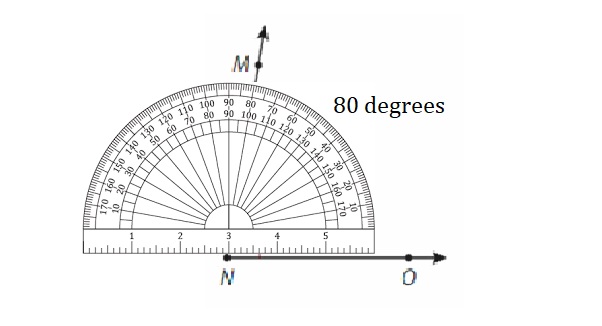
Question 4.
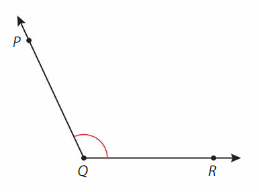
Answer:
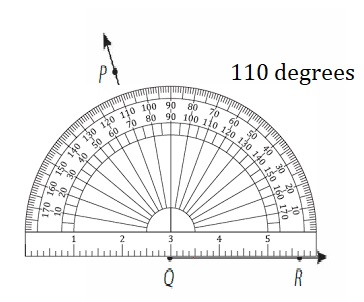
Use a protractor to draw the angle.
Question 5.
25°
Answer:
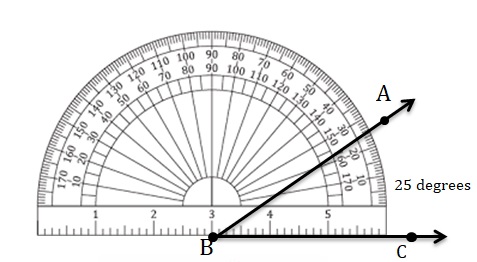
Question 6.
160°
Answer:
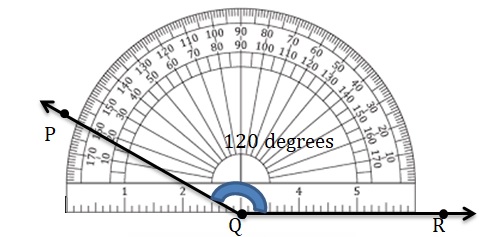
Question 7.
180°
Answer:
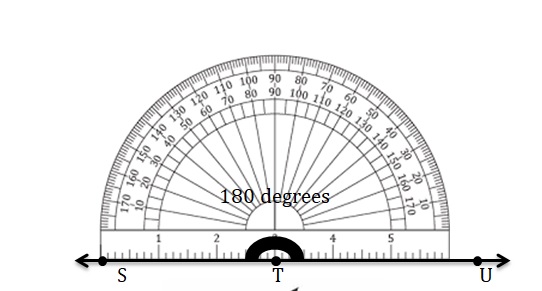
Question 8.
48°
Answer:
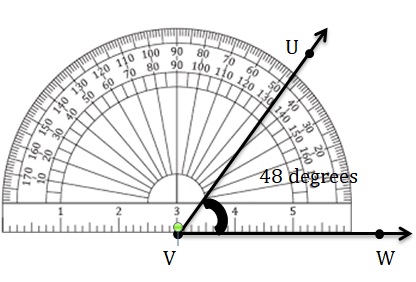
Question 9.
Writing
Why does one side of the angle you are measuring have to be lined up with the straight side of the protractor?
Answer:
We see two sets of degrees along the edge: an inner and outer scale. Both scales go from 0 to 180, but they run in opposite directions. If the angle opens to the right side of the protractor, use the inner scale. If the angle opens to the left of the protractor, use the outer scale.
To mark 0° on the inner scale of the protractor. So that we can next mark the angle we want to measure.
Question 10.
Precision
Newton says the measure of ∠ABC is 130°. Explain what he did wrong.
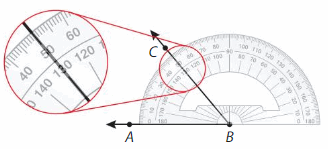
Answer:
The ∠ABC is 50 degrees not 130 degrees .
To measure an angle ABC, we place the mid point of the protractor on the vertex B of the angle. The base AB arm falls along with the base line of the protractor as shown in the figure above
The angle is measured on the protractor counting from 0 up to the point where the arm BC lies. In the above figure ∠ABC = 50°.
Think and Grow: Modeling Real Life
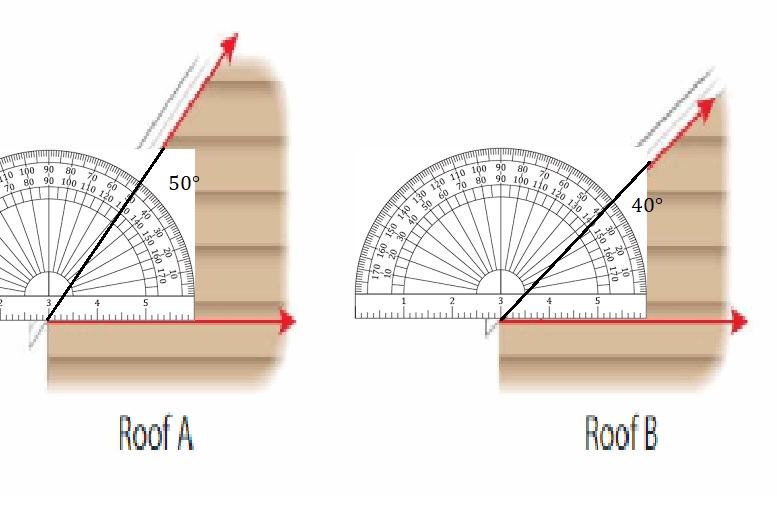
Example
A contractor builds two roofs. How much greater is the angle measure of Roof A than the angle measure of Roof B?
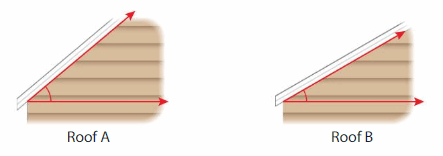
Use a protractor to measure the angle of each roof.
The angle measure of Roof A is _50°_ and the angle measure of Roof B is _40°__.
Subtract the angle measure of Roof B from the angle measure of Roof A.
_50°__ − _40°__ = _10°__
The angle measure of Roof A is _10°__ greater than the angle measure of Roof B.
Show and Grow0
Question 11.
An inspector compares two ramps. How much greater is the angle measure of Ramp B than the angle measure of Ramp A?
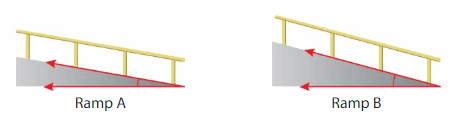
Answer:
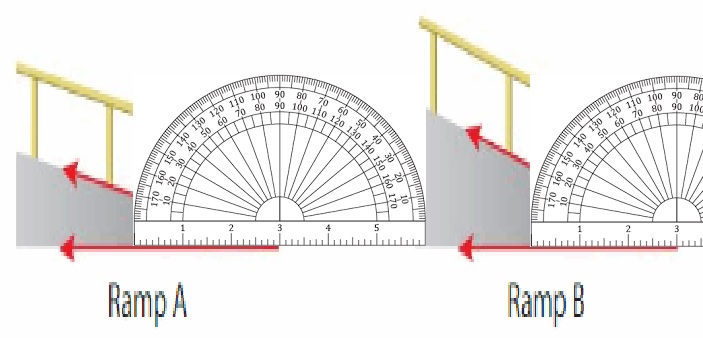
Ramp A angle is 10 degrees and Ramp B angle is 20 degrees
Ramp B angle is 10 degrees greater.
Question 12.
DIG DEEPER!
On a trail map, two straight trails intersect. One of the angles formed by the intersection is 70. What are the other three angle measures?
Answer:
A trail is formed with 4 angles.
Sum of the angles in trial = 360°.
if one angle =70°
Sum of other 3 angles = 360° – 70° = 290 °.
Measure and Draw Angles Homework & Practice 13.6
Find the measure of the angle. Then classify it.
Question 1.
Answer:
Question 2.

Answer: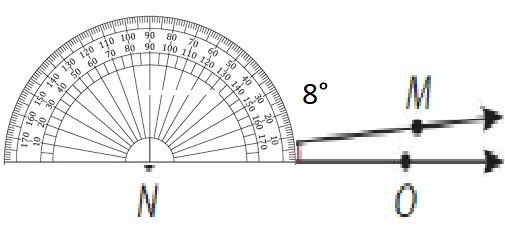
Use a protractor to draw the angle.
Question 3.
40°
Answer:
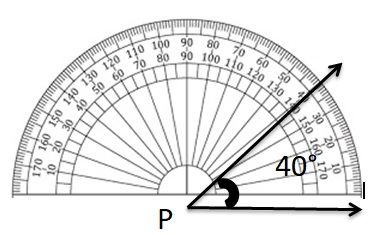
Question 4.
125°
Answer:
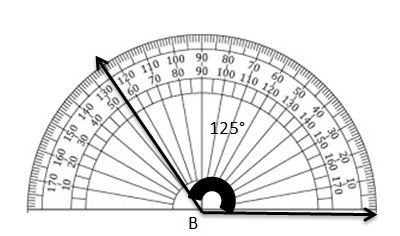
Question 5.
Reasoning
Measure the angles of each quadrilateral. What do you notice about the sum of the angle measures of each quadrilateral?
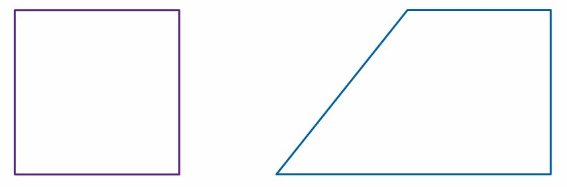
Answer:
The angles of the square are 90° each .
The angles of Quadilateral are two angles are 90°.
And other angles are 50°.
For every quadrilateral, the sum of the interior angles will always be 360°.
Question 6.
Precision
Use a protractor to draw a triangle with the angle measures of 0°. Describe your drawing.
Answer:
Question 7.
DIG DEEPER!
Use a protractor to draw a triangle with the angle measures of 90°, 35°, and 55°.
Answer:
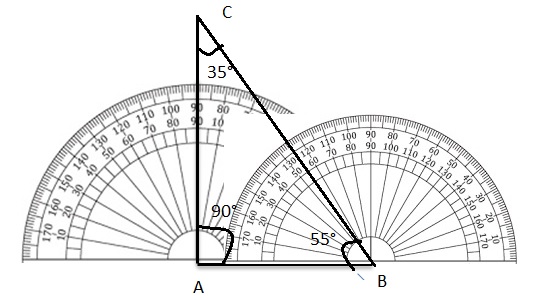
Question 8.
Modeling Real Life
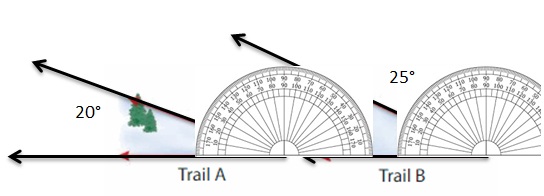
A snowboarder compares 2 mountain trails. How much greater is the angle measure of Trail B than the angle measure of Trail A?
Answer:
The angle is 5° greater.
Question 9.
DIG DEEPER!
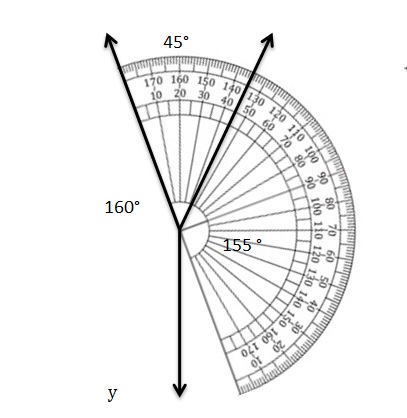
On a map, there is a Y-intersection where one straight road branches off into two straight roads. One of the angles formed by the intersection measures 45°. Give two possible measures for the other angles formed by the intersection.
Answer:
Review & Refresh
Find the equivalent length
Question 10.
5 km = ___ m.
Answer:
1km = 1000m
5 km = 5 x 1000 m = 5000m
Question 11.
7 m = ___ mm.
Answer:
1m = 1000mm
7 m = 7 x 1000 mm = 7000mm
Lesson 13.7 Add Angle Measures
Explore and Grow
Use a protractor to draw ∠PQR that measures 70°.
Draw another angle that measures 30° and shares side \(\overrightarrow{\mathrm{Q} R}\). Label your angle. How many angles are in your figure? What do you notice about their measures?

Make a copy of ∠PQR. Draw and label a different angle that measures 30° and shares \(\overrightarrow{\mathrm{Q} R}\). How many angles are in your figure? What do you notice about their measures?
Construct Arguments
What conclusions can you make from your figures above?
Answer:
The Above triangle formed is a scalene triangle- has no equal side.
Think and Grow: Add Angle Measures
When an angle is decomposed into parts that do not overlap, the angle measure of the whole equals the sum of the angle measures of the parts.
Two angles are adjacent when they share a common side and a common vertex, but no other points in common. When two or more adjacent angles form a larger angle, the sum of the measures of the smaller angles is equal to the measure of the larger angle.

Example
Find the measure of ∠WXY.
∠WXY and ∠ZXY are adjacent. The measure of ∠WXZ is equal to the sum of the measures of and ∠ZXY. Complete the equation.
_41°__ + __32°_ = _73°__
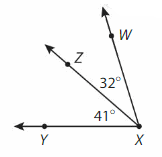
So, the measure of ∠WXY is _73°__.
Show and Grow
Question 1.
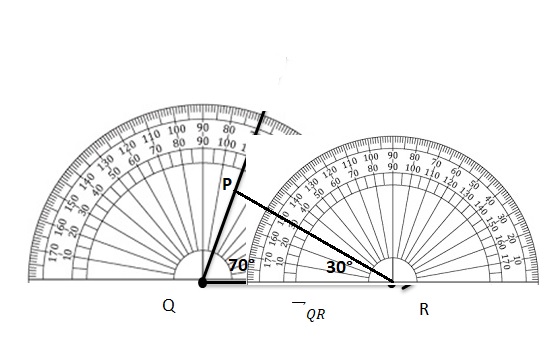
Complete the equation to find the ∠PQR.
Answer:
∠PQR = ∠PQS +∠SQR
= 43° + 77° =120°
Question 2.
Use a protractor to find the measure of each angle in the circle. Use the angle measures to complete the equation.
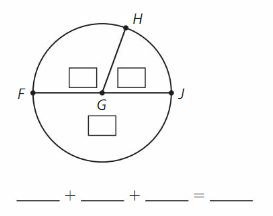
Answer:
Apply and Grow: Practice
Write an equation to find the measure of the angle.
Question 3.
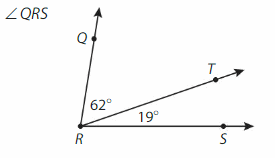
Answer:
∠QRS= ∠QRT +∠TRS
= 62° + 19° =81°
Question 4.
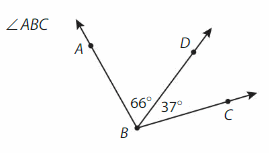
Answer:
∠ABC = ∠ABD +∠DBC
= 66° + 37° =103°
Question 5.
Answer:
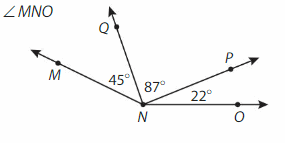
∠MNO = ∠MNQ +∠QNP +∠PNO
= 45° + 87° +22°
=154° .
Question 6.
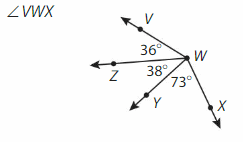
∠VWX = ∠VWZ +∠ZWY +∠YWX
= 36° + 38° +73°
=147° .
Use a protractor to find the measure of each angle in the circle. Use the angle measures to write an equation.
Question 7.
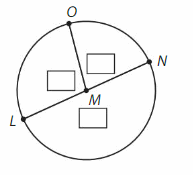
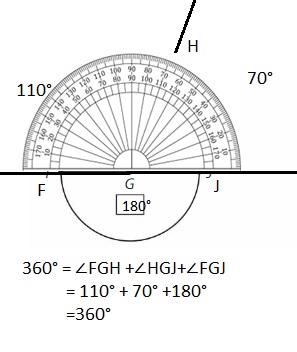
Answer:
∠M= ∠LMO +∠OMN +∠LMN
= 100° + 80° +180°
=360°
 ° .
° .
Question 8.
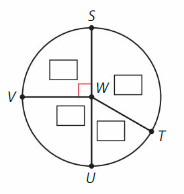
Answer:
∠W= ∠SWT +∠TWU +∠UWV +∠VWS
= 120° + 60° + 90° + 90°
=360°
Question 9.
Number Sense
The sum of seven adjacent angle measures that share a vertex is 154°. Each angle has the same measure. What is the measure of each angle?
Answer:
The sum of seven equal angles = 154°.
Measure of each angle = 154°/7 = 22°.
Question 10
DIG DEEPER!
∠PRS is adjacent to ∠QRS in Exercise 3. The measure of ∠PRS is 9°. Find the measure of ∠QRP. Classify angle ∠QRP.
Answer:
∠QRP = 9°
Two angles are adjacent when they share a common side and a common vertex, but no other points in common. When two or more adjacent angles form a larger angle, the sum of the measures of the smaller angles is equal to the measure of the larger angle.
Think and Grow : Modeling Real Life
Example
A store installs 3 security cameras on the same light post. Each camera has a viewing angle of 28°. The viewing angles of the cameras are adjacent. What is the total viewing angle of the cameras?
Add the viewing angle measures of the cameras.
28° + 28° + 28° = _84°__
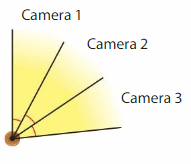
The total viewing angle of the cameras is __84°_
Show and Grow
Question 11.
A landscaper installs 3 sprinklers in 1 location in the grass. Each sprinkler has a spraying angle of 90°. The spraying angles of the sprinklers are adjacent. What is the total spraying angle of the sprinklers?
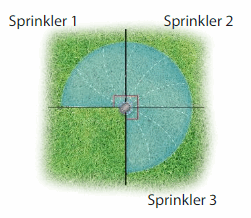
Answer:
As 3 sprinklers are adjacent all the 3 angles are equal.
Each angle of the sprinkler = 90°
Total spraying angle of the sprinklers= 3 X 90° = 270°
Question 12.
DIG DEEPER!
You use 4 rhombus tiles and 4 trapezoid tiles to make the pattern for a mosaic. Each tile is the same size and shape as a pattern block. What is the measure ∠NUQ?

Answer:
As we know th pattern blocks of trapezoid have 60° and rhombus have 30°.
Each tile is the same size and shape as a pattern block
∠NUQ= 30° + 60°+ 60° =150°
Question 13.
DIG DEEPER!
You make the pattern for a quilt. Each rhombus is the same size and shape. Name all of the 60° angles in the pattern.
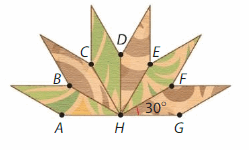
Answer:
All 60° angles in the pattern = ∠AHC +∠BHD +∠CHE+∠DHF +∠EHG.
Add Angle Measures Homework & Practice 13.7
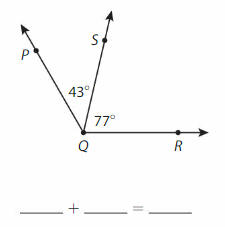
Write an equation to find the measure of the angle.
Question 1.
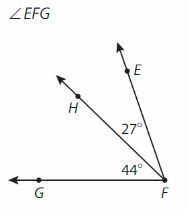
Answer:
∠EFG= ∠EFH +∠HFG
= 27° + 44°
=71°
Question 2.
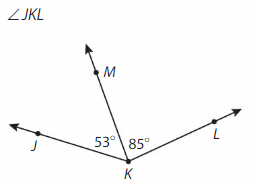
Answer:
∠JKL= ∠JKM +∠MKL
= 53° + 85°
=138°
Question 3.
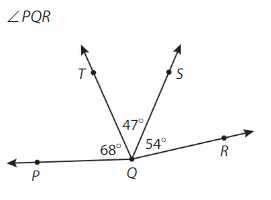
Answer:
∠PQR= ∠PQT +∠TQS +∠SQR
= 68° + 47° +54°
=316°
Question 4.
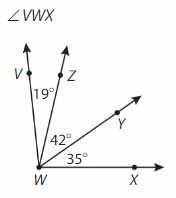
Answer:
∠VWX= ∠VWZ +∠ZWY +∠YWX
= 19° + 42° +35°
=96°
Use a protractor to find the measure of each angle in the circle. Use the angle measures to write an equation.
Question 5.
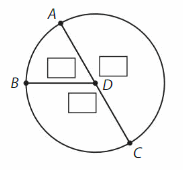
Answer:
∠D= ∠CDB +∠BDA +∠ADC
= 120° + 60° +180°
=360°
Question 6.
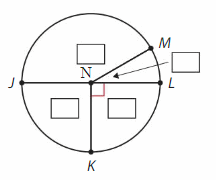
Answer:
∠N= ∠JNM +∠MNL +∠LNK + ∠KNJ
= 150° + 30°+90° + 90°
=360°
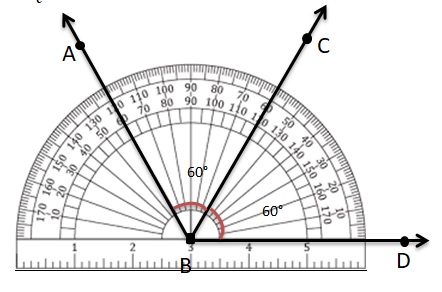
Question 7.
Open-Ended
Is it possible for the sum of two acute adjacent angle measures to be greater than the measure of a right angle? If so, draw a sketch to support your answer.
Answer:
Here ∠ABC and ∠CBD are both acute angles.
∠ABD= ∠ABC +∠CBD
= 60°+60°
=120°
sum of two acute adjacent angle=120° is more than 90° .
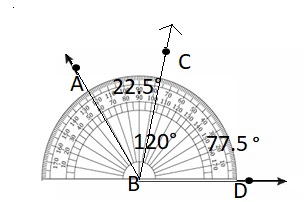
Question 8.
DIG DEEPER!
Use a protractor to measure the angle. Then decompose the angle into 2 parts so that one part is 25° greater than the other. What is the measure of each part?
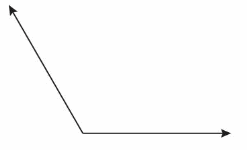
Answer:
The measure of given angle = 120°
The given angle is divided into two parts one angle is 25° greater than other.
The measure each part = a + ( a + 25°) = 120°
120° – 25° =2a
105° = 2a
a=55.5°
a + 25° = 77.5°
Question 9.
Modeling Real Life
A carpenter glues 3 identical pieces of wood next to each other to make the table shown. The 30° angles of the pieces of wood are adjacent. What is the total angle of the table formed by the pieces of wood?
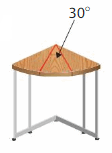
Answer:
Angle of each wood piece = 30°
As all angles are adjacent so angle of other wood pieces will be same.
so all 3 angles = 30° each.
Total angles = 3 x 30° = 90° .
Question 10.
DIG DEEPER!
You use 3 triangle pattern blocks and 3 rhombus pattern blocks to make the pattern for an art project. What is the measure of ∠ADE?
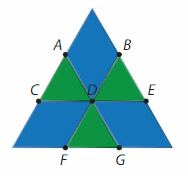
Answer:
The pattern block angle of triangle = 60°
The pattern block angle of Rhombus = 60°
∠ADE = ∠ADB + ∠BDE. = 60°+60° =120°
Review & Refresh
Compare
Question 11.
![]()
Answer:
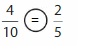
Question 12.
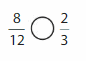
Answer:
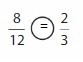
Question 13.
![]()
Answer:
![]()
Lesson 13.8 Find Unknown Angle Measures
Explore and Grow
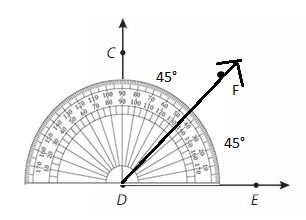
Draw and label ∠EDF where point F is between the rays of ∠CDE. Explain how you can find the measure of ∠CDF.
Answer:
∠CDE=∠CDF + ∠EDF
= 45 + 45 =90° (USING PROTACTOR).
Explanation:
Draw and label ∠LMP. Explain how you can find the measure of ∠NMP.
Answer:
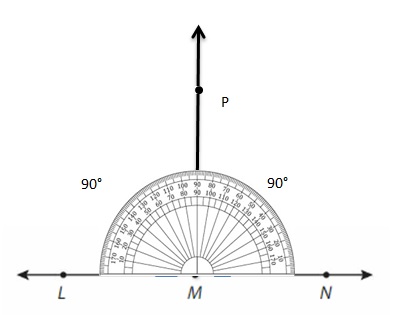
Reasoning
Draw ![]() in your figure above. Explain how you can find all of the angle measures in your figure. What do you notice?
in your figure above. Explain how you can find all of the angle measures in your figure. What do you notice?
Answer:
![]() is a which bisect the LN. so angles are divided into 2 parts equally. Using protractor we can find the measure of the angles.
is a which bisect the LN. so angles are divided into 2 parts equally. Using protractor we can find the measure of the angles.
This are complementary angles.
Think and Grow: Find Unknown Angle Measures

Example
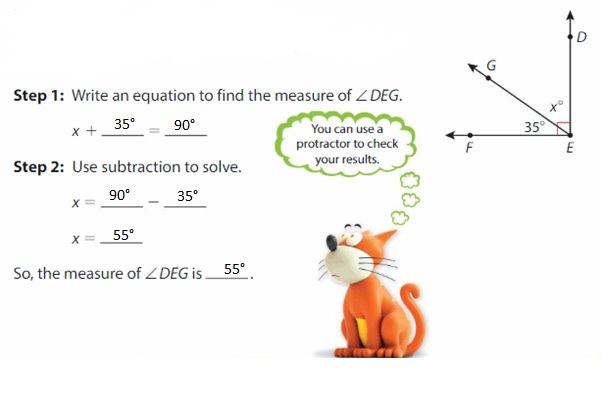
Find the measure of ∠DEG.
∠DEG and ∠GEF are complementary. The sum of their measures is 90.°
Step 1: Write an equation to find the measure of ∠DEG.

Answer:
Show and Grow
Question 1.
Write and solve an equation to find the measure of ∠NLM.
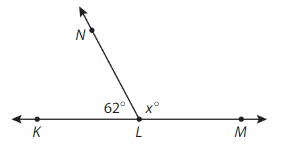
Answer:
Supplementary angles form a straight line and have a sum of 180 degrees.
∠NLM=180°- ∠KLN
= 180° – 62° = 118°
Apply and Grow: Practice
Write and solve an equation to find the measure of the angle.
Question 2.
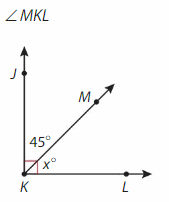
Answer:
Complementary angles form a right angle (L shape) and have a sum of 90 degrees.
∠MKL=90°- ∠MKJ
= 90° – 45° = 45°
Question 3.
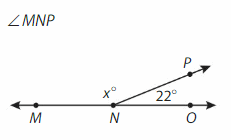
Answer:
Supplementary angles form a straight line and have a sum of 180 degrees.
∠MNP=180°- ∠PNO
= 180° – 22° = 158°
Question 4.
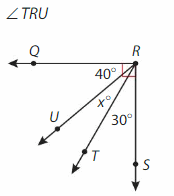
Answer:
∠TRU= ∠SRQ -∠SRT -∠URQ
= 90° – 30° – 40°
=20°
Question 5.
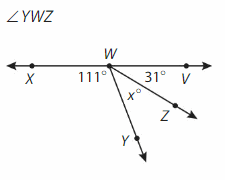
Answer:
∠YWZ= ∠XWV -∠VWZ -∠YWX
= 180° – 31°-111°
=38°
Question 6.
Find the measures of ∠AEB, ∠AED, and ∠DEC.
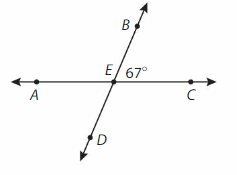
∠AEB= ∠AEC -∠BEC
= 180° – 67° = 113°
∠DEC= ∠DEB -∠BEC
= 180° – 67° = 113°
∠AED= ∠AEC -∠DEC
= 180° – 113° = 67°
Question 7.
DIG DEEPER!
Write and solve equations to find the measure of ∠KMJ.
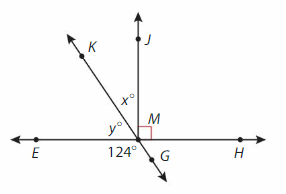
Answer:
∠KME= ∠KMG -∠GME
= 180° – 124° = 56°
∠KMJ= ∠JME -∠KME
= 90° – 56° = 34°
Question 8.
Writing
Define complementary angles and supplementary angles in your own words.
Answer:
Complementary angles form a right angle (L shape) and have a sum of 90 degrees.
Supplementary angles form a straight line and have a sum of 180 degrees.
Think and Grow: Modeling Real Life
Example
The foul lines on a baseball field are perpendicular. A baseball player hits a ball as shown. What is the measure of the angle between the path of the ball and the 1st base foul line?
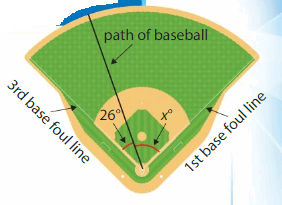
Think: What do you know? What do you need to find? How will you solve?
The 3rd base foul line and 1st base foul line are perpendicular.
So, the measure of the angle between the foul lines is _90° __.
Write an equation to find the measure of the angle between the path of the ball and the 1st base foul line.


Show and Grow
Question 9.
Runway 1 and Runway 2 are perpendicular. What is the measure of the missing angle between Runway 1 and Runway 3?
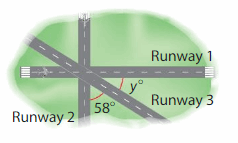
Answer:
Angle between Runway 1 and Runway 3= 90 – Angle between Runway 2 and Runway 3.
=90 – 58 =32°
Question 10.
DIG DEEPER!
What is the measure of the missing g angle between View Street and Elm Street?
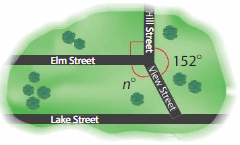
Answer:
Angle between View Street and Elm Street=360 – Angle between IIIstreet and view street – Angle between elm street and IIIstreet.
=360- 90 -152
=118°
Find Unknown Angle Measures Homework & Practice 13.8
Write and solve an equation to find the measure of the angle.
Question 1.
∠JKM
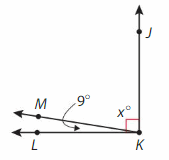
Answer:
∠JKM= ∠JKL -∠MKL
= 90° – 9° = 81°
Question 2.
∠PNM
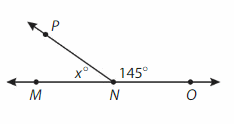
∠PNM= ∠MNO -∠PNO
= 180° – 145° = 35°
Question 3.
∠QRU
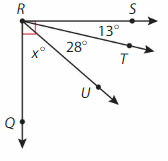
Answer:
∠QRU= ∠QRS -∠URT-∠TRS
= 90°-28° – 13°
=49°
Question 4.
∠ZWV
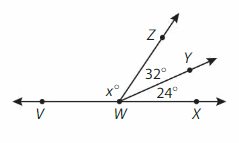
Answer:
∠ZWV= ∠VWX -∠ZWY-∠YWX
= 180°- 32° – 24°
=124°
Question 5.
Reasoning
∠ABC and ∠CBD are adjacent. ∠ABC is a right angle.
∠CBD is acute.
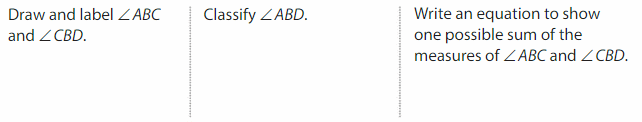
Answer:
∠ABD=∠ABC-∠CBD
= 90 – 35 = 65°
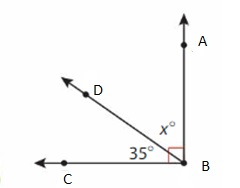
Question 6.
Structure
Which equations can you use to find the measure of angle ∠MKJ?
Answer:
180 – 57 = x
Question 7.
Open-Ended
An acute angle and an obtuse angle are adjacent and supplementary. What might the measures of each angle be?
Answer:
Question 8.
Modeling Real Life
Newton bounces a ball off of a wall to Descartes. \(\overline{A D}\)⊥\(\overline{D B}\). The measures of ∠ADC and ∠BDE are equivalent. Find the measures of ∠ADC and ∠BDE.
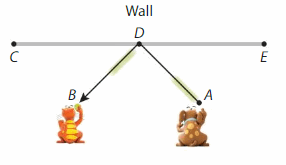
Answer:
∠ADC and ∠BDE. are equal
∠CDE= ∠ADC + ∠BDE – ∠BDA.
180 = a + a – ∠BDA.
∠BDA.=180 -2a
Question 9.
Modeling Real Life
Owls see an object with both eyes at the same time using binocular vision. What angle measure describes the owl’s binocular vision? Explain.
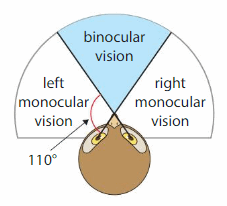
Answer:
left monocular + Binocular vision = 180
Binocular vision = 180 – 110=70 degrees.
Review & Refresh
Write the fraction as a money amount and as a decimal
Question 10.
\(\frac{49}{100}\)
Answer:
0.49
Question 11.
\(\frac{25}{100}\)
Answer:
0.25
Question 12.
\(\frac{7}{100}\)
Answer:
0.07
Identify and Draw Lines and Angles Performance Task 13
A rural town is expanding and needs to plan the construction of new roads.
Question 1.
What is another name for Main Street?
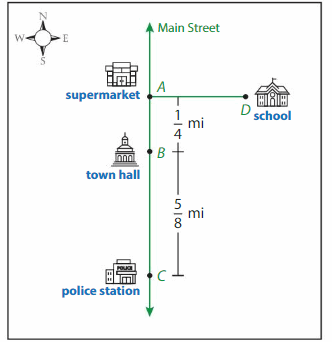
Answer:
Line AC.
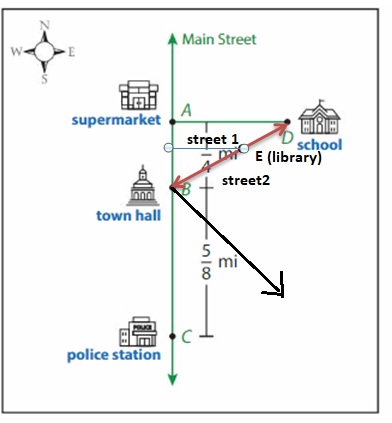
Question 2.
Use the directions to complete the map.
a. Draw ![]() and label it with a street name of your choice.
and label it with a street name of your choice.
b. The library will be at point E on ![]() and on the other side of Main Street as the school. Plot and label the library E at point E.
and on the other side of Main Street as the school. Plot and label the library E at point E.
c. Draw a new road through point E that is perpendicular to Main Street. Label it with a street name of your choice.
Question 3.
City planners want to construct a new residential neighborhood southeast of the town hall.
a. The measure of ∠ABD is \(\frac{1}{6}\) of 360°. What is the measure of the angle?
Answer:
∠ABD=(1/6) x 360 =60 degree.
b. Classify ∠DBC. What is its measure?
Answer:
∠DBC=180 -∠ABD = 180-60 = 120 degrees.
c. Draw a road from point B to the new neighborhood. The road divides ∠DBC exactly in half.
Answer:
Question 4.
Is the distance between the supermarket and the police station more than or less than a mile? Explain.
Answer:
Distance between the supermarket and the police station= AB + BC
= (1/4) + (5/8).
=(2+5)/8
=7/8.=0.8 mile
which is less than 1 mile.
Identify and Draw Lines and Angles Activity
Geometry Dots
Directions:
- Players take turns connecting two dots, each using a different color.
- On your turn, connect two dots, vertically or horizontally. If you close a square around an angle, find the measure of the angle inside the square. If you do not close a square, your turn is over.
- Continue playing until you find all of the angle measures.
- The player that finds the most angle measures wins!
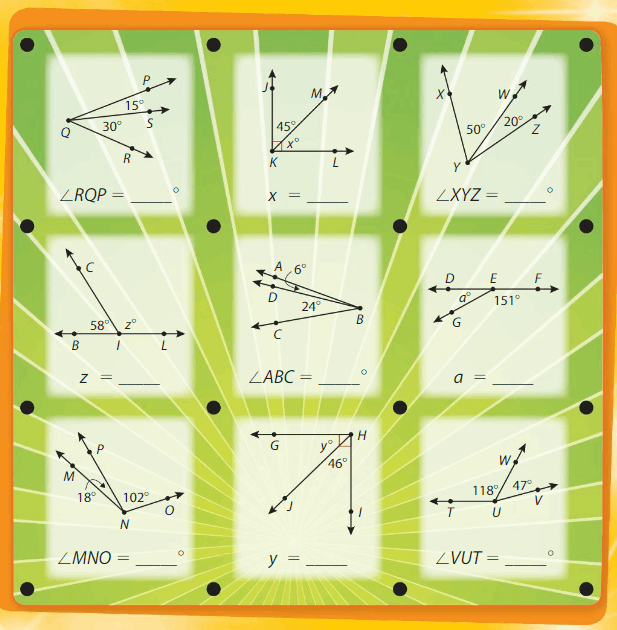
Answer:
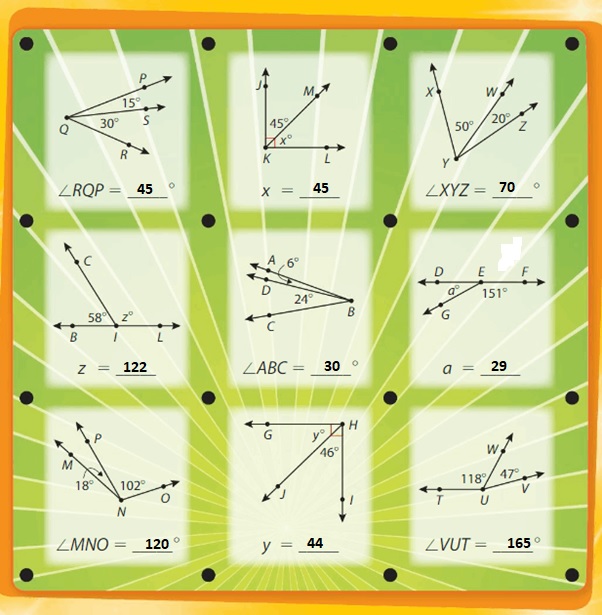
Identify and Draw Lines and Angles Chapter Practice 13
13.1 Points, Lines and Rays
Name the figure. Write how to say the name.
Question 1.
![]()
Answer:
It is a point said as Point F
Question 2.
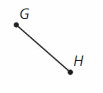
Answer:
It is said as line GH. and represented as GH with overhead arrow.
Question 3.

Answer:
It is a ray JK .It is represented with Over head arrow to left.
Draw and label the figure.
Question 4.
![]()
Answer:
Question 5.
![]()
Answer:
Question 6.
![]()
Answer:

Use the figure
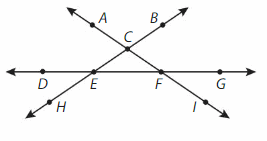
Question 7.
Name a line segment.
Answer: CE
Question 8.
Name two different rays.
Answer: CA and CB.
13.2 Identify and Draw Angles
Question 9.
Write a name for the angle and classify it.
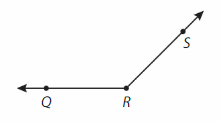
Answer:
∠SRQ. It is a obtuse angle.
Question 10.
∠TUV is a right angle. Draw and label the angle.
Answer:
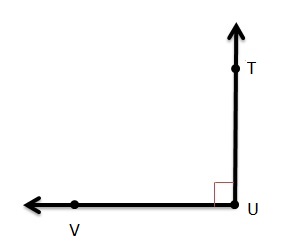
13.3 Identify Parallel and Perpendicular Lines
Draw and label the lines with the given description.
Question 11.
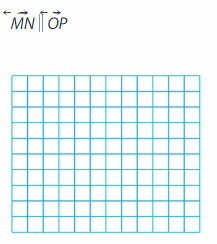
Answer:
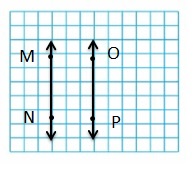
Question 12.

Answer:
13.4 Understand Degrees
Find the measure of each angle.
Question 13.
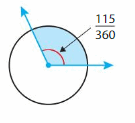
Answer:
115°
Question 14.
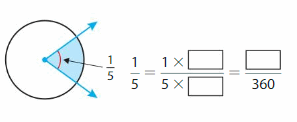
Answer:
=(1/5) x(—–/—–)= —-/360.
=72°/360°
Question 15.
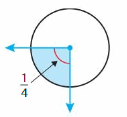
Answer:
=1/4 x 360
=90°
Question 16.
A circle is divided into 12 equal parts. What is the measure of the angle that turns through 2 parts?
Answer:
Number parts divided = 12
Total sum of the angles = 360°
Angle of 1 part = 360°/12. = 30°.
The measure of the angle that turns through 2 parts = 2 x 30°. = 60°.
Question 17.
Which one Doesn’t Belong? Which angle measure does not belong with the other three?
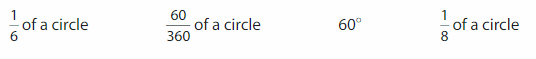
Answer:
1/6 of a circle = 360/6 = 60°.
60/360 of a circle = 1/6.
60°
1/8 of a circle = 360°/8=45°
Therefore 1/8 of a circle is different.
13.5 Find Angle Measures
Use pattern blocks to find the measure of the angle.
Question 18.
Answer:
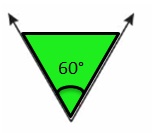
Question 19.

Answer:
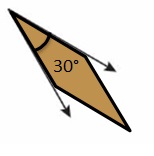
Question 20.
Answer:
Question 21.
Answer:
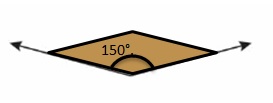
13.6 Measure and Draw Angles
Question 22.
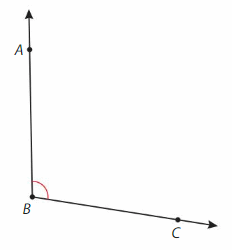
Find the measure of the angle. Then classify it.
Question 23.
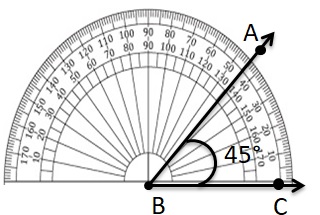
Use a protractor to draw a 45° angle.
Answer:
Modeling Real Life
On a map, two straight railroad tracks intersect. One of the angles formed by the intersection is 30°. What are the three other angle measures?
13.7 Add Angle Measures
Question 25.
Write an equation to find the measure ∠EFG.
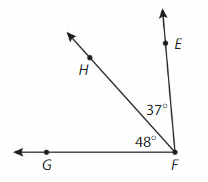
Answer:
∠EFG = ∠EFH+∠HFG.
=37° + 48° = 85°.
Question 26.
Use a protractor to find the measure of each angle in the circle. Use the angle measures to write an equation.
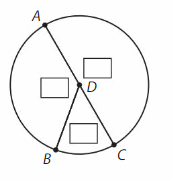
Answer:
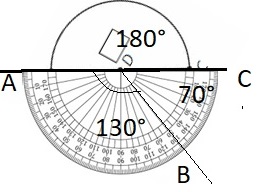
13.8 Find Unknown Angle Measures
Write and solve an equation to find the measure of the angle.
Question 27.
Answer:
Complementary angles =90°.
∠ABD = ∠ABC-∠DBC.
=90°-27° = 63°.
Question 28.
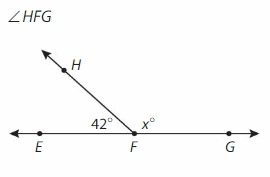
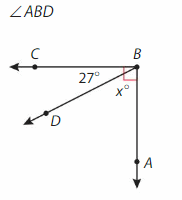
Answer:
Supplementary angle =180°
∠HFG = ∠EFG-∠EFH.
=180° + 42° = 38°.
Question 29.
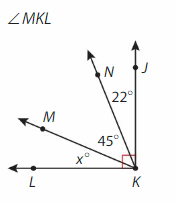
Answer:
Complementary angles =90°.
∠MKL = ∠LKJ-∠MKN-∠NKJ.
=90°-45°-22°= 23°.
Question 30.
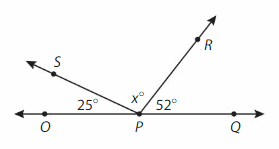
Answer:
Supplementary angles =180°.
∠SPR = ∠OPQ-∠OPS-∠RPQ.
=180°-25°-52°= 103°.
Conclusion:
The solutions provided in the Big Ideas Math Answers Grade 4 Chapter 13 Identify and Draw Lines and Angles are prepared by the subject experts. So Download Bigideas Math Answers Grade 4 Chapter 13 Identify and Draw Lines and Angles for free and start practicing the problems. Also, bookmark our page to get the Solution Key of Big Ideas Math Grade 4 Chapters.