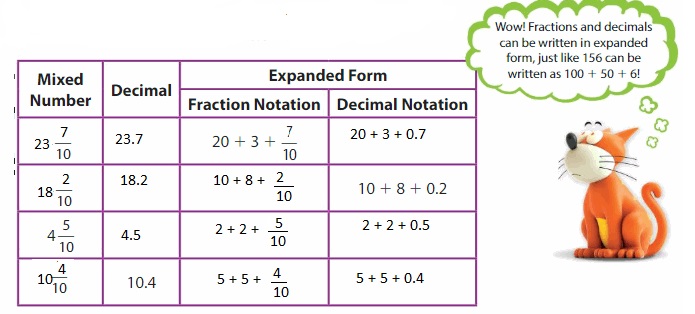
Big Ideas Math Answers Grade 4 Chapter 10 Relate Fractions and Decimals: If you are an avid student and curious about Maths then take the help of the Big Ideas Math Answers Grade 4 Chapter 10 Relate Fractions and Decimals. You can explore Questions from Practice Tests, Cumulative Practice, Chapter Test, Performance Tests, and seek the Homework Help required. Big Ideas Math Answers Grade 4 Chapter 10 Relate Fractions and Decimals provided will enhance the Overall Maths Skills.
Big Ideas Math Book 4th Grade Answer Key Chapter 10 Relate Fractions and Decimals
In order to help you guys, we have provided the solutions in pdf format. So Download Big Ideas Math Book 4th Grade Answer Key Chapter 10 Relate Fractions and Decimals pdf for free. Access the topicwise Grade 4 Big Ideas Math Answer Key available via quick links and use them as a reference whenever you have any queries.
Lesson: 1 Understand Tenths
Lesson: 2 Understand Hundredths
Lesson: 3 Fractions and Decimals
Lesson: 4 Compare Decimals
Lesson: 5 Add Decimal Fractions and Decimals
- Lesson 10.5 Add Decimal Fractions and Decimals
- Add Decimal Fractions and Decimals Homework & Practice 10.5
Lesson: 6 Fractions, Decimals and Money
Lesson: 7 Operations with Money
Performance Task
- Relate Fractions and Decimals Performance Task 10
- Relate Fractions and Decimals Activity
- Relate Fractions and Decimals Chapter Practice 10
Lesson 10.1 Understand Tenths
Explore and Grow
How many dimes have a total value of one dollar? Draw a model.

One dime is what fraction of one dollar? Write your answer in words and as a fraction.
Answer:
We know that,
1 dollar = 10 dimes
So,
The representation of one dime in the fraction of 1 dollar is: \(\frac{1}{10}\)
In terms of words, one Dime is equal to one-tenth of the Dollar
Explanation:
The given note is “Dollar note”

We know that,
1 Dollar = 10 Dimes
So,
The representation of one Dime in the fraction of 1 dollar is: \(\frac{1}{10}\)
So,
The representation of a Dime in the model is:
From the above model,
We can say that one Dime is equal to one-tenth of one Dollar.
Structure
How is one whole related to one-tenth? How do you think you can write \(\frac{1}{10}\) in a place value chart?
Answer:
The representation of one-tenth in a place value chart is:
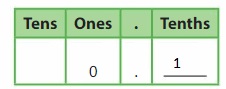
Explanation:
The one-tenth is the fraction value which is less than one whole. When we divide the one whole into ten parts,
then each divided part represents one-tenth of the 10 parts.
Hence,
The representation of \(\frac{1}{10}\) in the place-value chart is:

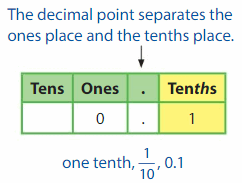
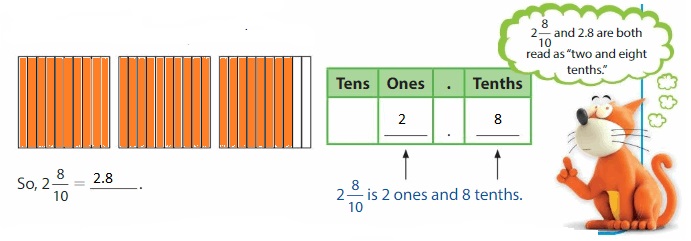
Think and Grow: Understand Tenths
A decimal is a number with one or more digits to the right of the decimal point. The first place to the right of the decimal point is the tenths place.
You can write tenths as fractions or decimals.
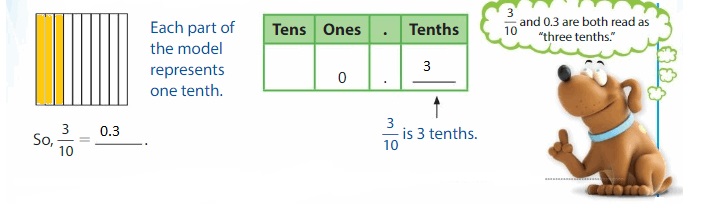
Example
Write \(\frac{3}{10}\) as a decimal.
Shade the model. Use a place value chart.
Example
Write 2\(\frac{8}{10}\) as a decimal.
Shade the model. Use a place value chart.
Show and Grow
Write the fraction or mixed number as a decimal.
Question 1.
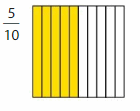
Answer: The representation of \(\frac{5}{10}\) in the place-value chart is:
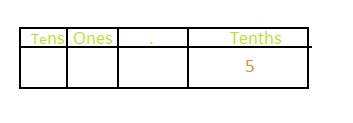
Explanation:
The given fraction is: \(\frac{5}{10}\)
The given model fro \(\frac{5}{10}\) is:

The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Question 2.

Answer: The representation of 1\(\frac{7}{10}\) in the place-value chart is:
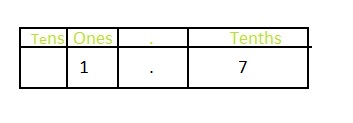
Explanation:
The given mixed fraction is: 1\(\frac{7}{10}\)
So,
The improper fraction of 1\(\frac{7}{10}\) is: \(\frac{17}{10}\)
The given model for 1\(\frac{7}{10}\) is:

Here,
In 1\(\frac{7}{10}\),
1 represents the one’s place and 7 represents the tenths place
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
So,
The representation of 1\(\frac{7}{10}\) in the decimal form is: 1.7
Apply and Grow: Practice
Shade the model to represent the fraction or mixed number. Then write the fraction or mixed number as a decimal.
Question 3.
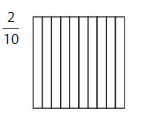
Answer: The representation of \(\frac{2}{10}\) in the place- value chart is:
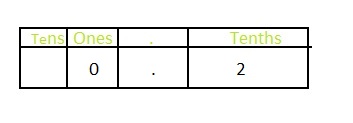
Explanation:
The given fraction is: \(\frac{2}{10}\)
The model representing the \(\frac{2}{10}\) is:
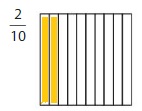
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Question 4.

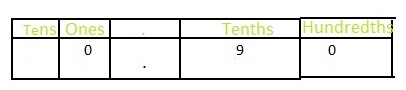
Answer: The representation of 1\(\frac{9}{10}\) in the place-value chart is:

Explanation:
The given mixed fraction is: 1\(\frac{9}{10}\)
So,
The improper fraction of 1\(\frac{9}{10}\) is: \(\frac{19}{10}\)
The model representiong 1\(\frac{9}{10}\) is:

The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 1\(\frac{9}{10}\) in the decimal form is: 1.9
Write the fraction or mixed number as a decimal.
Question 5.
![]()
Answer: The representation of \(\frac{7}{10}\) in the place-value chart is:
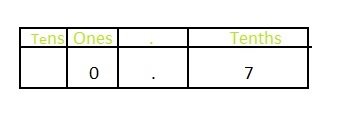
Explanation:
The given fraction is: \(\frac{7}{10}\)
The model representing the \(\frac{7}{10}\) is:
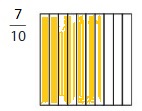
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{7}{10}\) in the decimal form is: 0.7
Question 6.
![]()
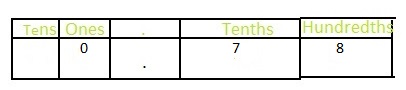
Answer: The representation of \(\frac{4}{10}\) in the place-value chart is:
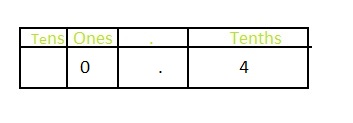
Explanation:
The given fraction is: \(\frac{4}{10}\)
The model representing the \(\frac{4}{10}\) is:
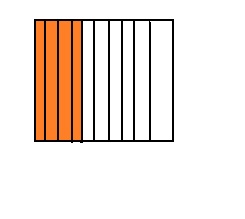
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{4}{10}\) in the decimal form is: 0.4
Question 7.
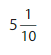
Answer: The representation of 5\(\frac{1}{10}\) in the place-value chart is:
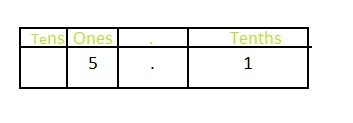
Explanation:
The given mixed fraction is:5\(\frac{1}{10}\)
So,
The improper fraction of 5\(\frac{1}{10}\) is: \(\frac{51}{10}\)
In 5\(\frac{1}{10}\),
5 represents the ones position and 1 represents the tenths position.
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 5\(\frac{1}{10}\) in the decimal form is: 5.1
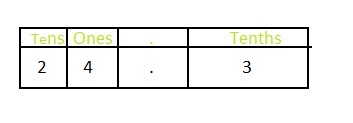
Question 8.
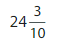
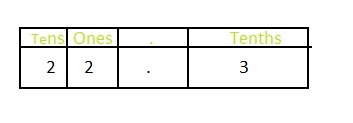
Answer: The representation of 24\(\frac{3}{10}\) in the place-value chart is:
Explanation:
The given mixed fraction is: 24\(\frac{3}{10}\)
So,
The improper fraction of 24\(\frac{3}{10}\) is: \(\frac{243}{10}\)
In 24\(\frac{3}{10}\),
2 represents the tens position
4 represents the one’s position
3 represents the tenths position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 24\(\frac{3}{10}\) in the decimal form is: 24.3
Write the number as a fraction or mixed number and as a decimal.
Question 9.
six tenths
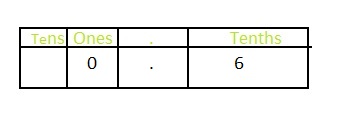
Answer: The representation of six tenths in the fraction form is: \(\frac{6}{10}\)
The representation of \(\frac{6}{10}\) in the place-value chart is:
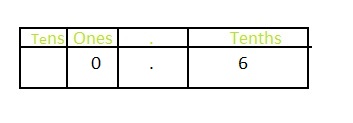
Explanation:
The given fraction is: \(\frac{6}{10}\)
In \(\frac{6}{10}\),
6 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{6}{10}\) in the Decimal form is: 0.6
Question 10.
eleven and five-tenths
Answer: The representation of eleven and five-tenths in the fraction form is: 11\(\frac{5}{10}\)
The representation of 11\(\frac{5}{10}\) in the place-value chart is:
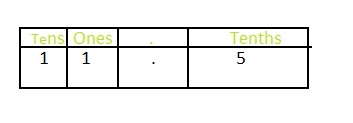
Explanation:
The given mixed fraction is: 11\(\frac{5}{10}\)
So,
The improper fraction of 11\(\frac{5}{10}\) is: \(\frac{115}{10}\)
In 11\(\frac{5}{10}\),
1 represents Ten’s and 1 represents the one’s position
5 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
the representation of 11\(\frac{5}{10}\) in the decimal form is: 11.5
Question 11.
Newton passes 8 out of 10 obedience classes. What portion of the classes does Newton pass? Write your answer as a decimal.

Answer: The portion of the classes does Newton pass is: 0.8
Explanation:
It is given that Newton passes 8 out of 10 obedience classes.
The representation of the portion of the classes that Newton passed in the fraction form = \(\frac{The number of classes that Newton passed} {The total number of classes}\) = \(\frac{8}{10}\)
So,
The representation of \(\frac{8}{10}\) in the place-value chart is:
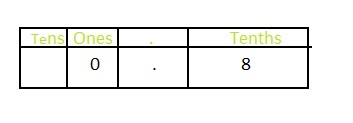
In \(\frac{8}{10}\),
8 represents the Tenth’s position.
So, the representation of \(\frac{8}{10}\) in the decimal form is: 0.8
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
We can conclude that the representation of the portion of the classes that Newton passed in the decimal form is: 0.8
Question 12.
You move a game piece around a game board 3\(\frac{2}{10}\) times before you lose a turn. Write this number as a decimal.

Answer: The representation of 3\(\frac{2}{10}\) in the decimal form is: 3.2
Explanation:
It is given that you move a game piece around a game board 3\(\frac{2}{10}\) times before you lose a sum.
So,
The representation of 3\(\frac{2}{10}\) in the place-value chart is:
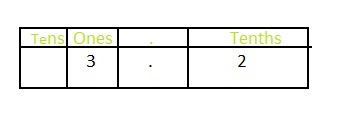
In 3\(\frac{2}{10}\),
3 represents one’s position
2 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 3\(\frac{2}{10}\) in the decimal form is: 3.2
Question 13.
Writing
Do 0.5 and 5.0 have the same value? Explain.
Answer: 0.5 and 5.0 does not have the same value because the place-value of 5 is different in both 0.5 and 5.0
Explanation:
The given numbers are: 0.5 and 5.0
The position of 5 in 0.5 according to the place-value chart is:
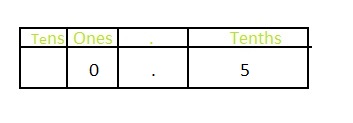
The position of 5 in 5.0 according to the place-value chart is:
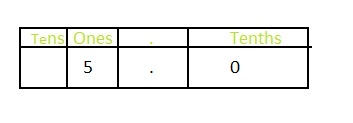
In 0.5, the position of 5 is: tenth’s position
In 5.0, the position of 5 is: One’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence, from the above,
We can conclude that 0.5 and 5.0 do not have the same value.
Think and Grow: Modeling Real Life
Example
You have a collection of dinosaur figurines. What portion of the dinosaurs in your collection are carnivores? Write your answer as a decimal.

Draw a model to represent the collection. Shade the same number of parts as there are carnivore dinosaurs in the collection.

Write the decimal shown by the model.
Answer:
From the above table, 3 of the dinosaurs in the collection are carnivores.
The total number of dinosaurs in the collection is: 10
So,
The representation of carnivores in the collection of dinosaurs is: \(\frac{3}{10}\)
Explanation:
The given table is:

From the above table,
The total number of dinosaurs are: 10
The number of carnivores in the total number of dinosaurs is: 3
So,
The representation of carnivores in the total number of dinosaurs in the fraction form is: \(\frac{3}{10}\)
Now,
The representation of \(\frac{3}{10}\) in the place-value chart is:
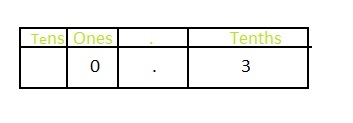
In \(\frac{3}{10}\),
3 represents tenth’s position.
The formula for converting a fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of carnivores from the total number of dinosaurs in the decimal form is: 0.3
Show and Grow
Question 14.
Use the table above. What portion of the dinosaurs in your collection are herbivores? Write your answer as a decimal.

Answer: The portion of dinosaurs in your collection that are herbivores is: 0.5
Explanation:
The given table is:

From the above table,
The total number of dinosaurs are: 10
The number of herbivores from the collection of dinosaurs is: 5
So,
The representation of the number of herbivores from the total dinosaurs in the fraction form is: \(\frac{5}{10}\)
Now,
The representation of \(\frac{3}{10}\) in the place-value chart is:
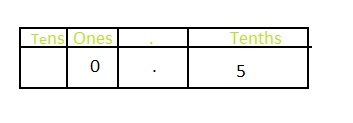
In \(\frac{3}{10}\),
3 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of the herbivores from the total number of dinosaurs in the decimal form is: 0.5
Question 15.
DIG DEEPER!
You have 10 apps on your tablet. Six of the apps are games. What portion of the apps on your tablet are not games? Write your answer as a decimal.
Answer: The portion of the apps on your tablet that is not games in the fraction form is: \(\frac{4}{10}\)
Explanation:
It is given that there are 10 apps on your tablet out of which 6 of the apps are games.
So,
The total number of apps on your tablet are: 10
The number of apps that are games on your tablet is: 6
So,
The number of apps that are not games on your tablet is: 4
So,
The representation of the apps that are not games out of the total apps in the fraction form is: \(\frac{4}{10}\)
So,
The representation of \(\frac{4}{10}\) in the place-value chart is:
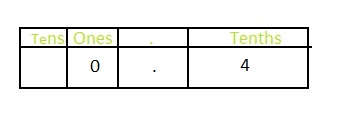
In \(\frac{4}{10}\),
4 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The portion of the apps that are not games out of the total number of apps in the decimal form is: 0.4
Question 16.
DIG DEEPER!
You make 3 pans of lasagna for a party. You cut each pan of lasagna into10 equal pieces. The guests eat 22 pieces. Write the fraction and decimal that represent how many pans of lasagna the guests eat.
Answer: The representation of the pans of lasagna the guests eat in the fraction form is: \(\frac{22}{30}\)
Explanation:
It is given that there are 3 pans of lasagna for a party and each pan of lasagna cut into 10 equal parts.
So,
The total number of pieces of Lasagna = The total number of pans × The number of parts that each Lasagna is cut
= 3 × 10 = 30 pieces
It is also given that the guests eat 22 pieces out of 30 pieces.
So,
The representation of the number of pieces that the guests eat is: \(\frac{22}{30}\)
The representation of \(\frac{22}{30}\) in the place-value chart is:
In \(\frac{22}{30}\),
22 represents the ten’s and one’s position
30 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of the number of pieces out of the total number of pieces in the decimal form is: 22.30
Understand Tenths Homework & Practice 10.1
Question 1
Write \(\frac{6}{10}\) as a decimal.

Answer: The representation of \(\frac{6}{10}\) in the decimal form is: 0.6
Explanation:
The given fraction is: \(\frac{6}{10}\)
The given model for \(\frac{6}{10}\) is:

The representation of \(\frac{6}{10}\) in the place-value chart is:
In \(\frac{6}{10}\),
6 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{6}{10}\) in the decimal form is: 0.6
Question 2.
Shade the model to represent 1\(\frac{8}{10}\). Then write the mixed number as a decimal.

Write the fraction or mixed number as a decimal.
Answer: The representation of 1\(\frac{8}{10}\) in the decimal form is: 1.8
Explanation:
The given mixed fraction is: 1\(\frac{8}{10}\)
So,
The improper fraction of 1\(\frac{8}{10}\) is: \(\frac{18}{10}\)
The model given for 1\(\frac{8}{10}\) is:
So,
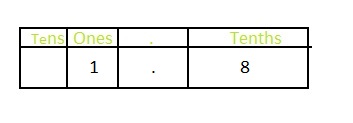
The representation of 1\(\frac{8}{10}\) in the place-value chart is:
In 1\(\frac{8}{10}\),
1 represents the one’s position
8 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
Th representation of 1\(\frac{8}{10}\) in the decimal form is: 1.8
Question 3.
\(\frac{1}{10}\)
Answer: The representation of \(\frac{1}{10}\) in the decimal form is: 0.1
Explanation:
The given fraction is: \(\frac{1}{10}\)
Now,
The representation of \(\frac{1}{10}\) in the place-value chart is:
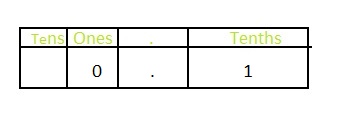
In \(\frac{1}{10}\),
1 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{1}{10}\) in the decimal form is: 0.1
Question 4.
\(\frac{5}{10}\)
Answer: The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Explanation:
The given fraction is: \(\frac{5}{10}\)
Now,
The representation of \(\frac{5}{10}\) in the place-value chart is:
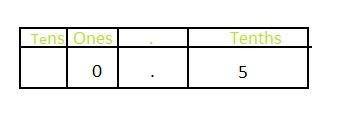
In \(\frac{5}{10}\),
5 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Question 5.
\(\frac{2}{10}\)
Answer: The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Explanation:
The given fraction is: \(\frac{2}{10}\)
Now,
The representation of \(\frac{2}{10}\) in the place-value chart is:
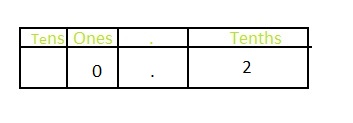
In \(\frac{2}{10}\),
2 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Question 6.
\(\frac{8}{10}\)
Answer: The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Explanation:
The given fraction is: \(\frac{8}{10}\)
Now,
The representation of \(\frac{8}{10}\) in the place-value chart is:
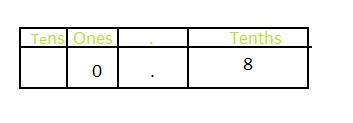
In \(\frac{8}{10}\),
8 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Question 7.
4\(\frac{3}{10}\)
Answer: The representation of 4\(\frac{3}{10}\) in the decimal form is: 4.3
Explanation:
The given mixed fraction is: 4\(\frac{3}{10}\)
So,
The improper fraction of 4\(\frac{3}{10}\) is: \(\frac{43}{10}\)
Now,
The representation of 4\(\frac{3}{10}\) in the place-value chart is:
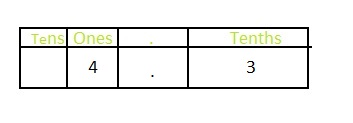
In 4\(\frac{3}{10}\),
4 represents the one’s position
3 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 4\(\frac{3}{10}\) in the decimal form is: 4.3
Question 8.
1\(\frac{4}{10}\)
Answer: The representation of 1\(\frac{4}{10}\) in the decimal form is: 1.4
Explanation:
The given mixed fraction is: 1\(\frac{4}{10}\)
So,
The improper fraction of 1\(\frac{4}{10}\) is: \(\frac{14}{10}\)
Now,
The representation of 1\(\frac{4}{10}\) in the place-value chart is:
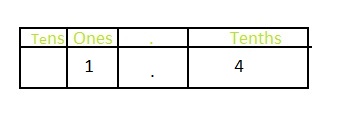
In 1\(\frac{4}{10}\),
1 represents the one’s position
4 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 1\(\frac{4}{10}\) in the decimal form is: 1.4
Question 9.
31\(\frac{7}{10}\)
Answer: The representation of 31\(\frac{7}{10}\) in the decimal form is: 31.7
Explanation:
The given mixed fraction is: 31\(\frac{7}{10}\)
So,
The improper fraction of 31\(\frac{7}{10}\) is: \(\frac{317}{10}\)
Now,
The representation of 31\(\frac{7}{10}\) in the place-value chart is:
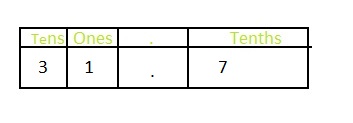
In 31\(\frac{7}{10}\),
3 represents the ten’s position
1 represents the one’s position
7 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 31\(\frac{7}{10}\) in the decimal form is: 31.7
Question 10.
40\(\frac{6}{10}\)
Answer: The representation of 40\(\frac{6}{10}\) in the decimal form is: 40.6
Explanation:
The given mixed fraction is: 40\(\frac{6}{10}\)
So,
The improper fraction of 40\(\frac{6}{10}\) is: \(\frac{406}{10}\)
Now,
The representation of 40\(\frac{6}{10}\) in the place-value chart is:
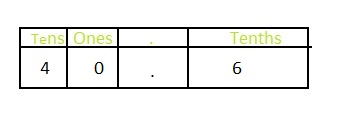
In 40\(\frac{6}{10}\),
4 represents the ten’s position
0 represents the one’s position
6 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 40\(\frac{6}{10}\) in the decimal form is: 40.6
Write the number as a fraction or mixed number and as a decimal.
Question 11.
three tenths
Answer: The representation of the three-tenths in the decimal form is: 0.3
Explanation:
The given fraction in the word form is: Three-tenths
The representation of the three-tenths in the fraction form is: \(\frac{3}{10}\)
So,
The representation of \(\frac{3}{10}\) in the place-value chart is:
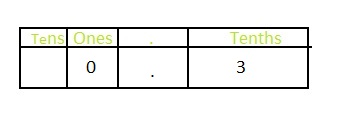
In \(\frac{3}{10}\),
3 represents the tenth’s place
Hence,
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Question 12.
fourteen and nine-tenths
Answer: The representation of fourteen and nine-tenths in the decimal form is: 14.9
Explanation:
The given mixed fraction in Word form is: fourteen and nine-tenths
The representation of fourteen and nine-tenths in the fraction form is: 14\(\frac{9}{10}\)
So,
The improper fraction of 14\(\frac{9}{10}\) is: \(\frac{149}{10}\)
So,
The representation of 14\(\frac{9}{10}\) in the place-value chart is:
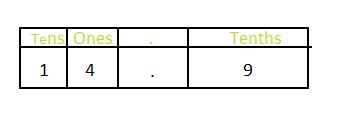
In 14\(\frac{9}{10}\),
1 represents the ten’s place
4 represents the one’s place
9 represents the tenth’s place
Hence,
The representation of 14\(\frac{9}{10}\) in the decimal form is: 14.9
Question 13.
You knock down 5 out of 10 bowling pins. What portion of the bowling pins do you knockdown? Write your answer as a decimal.
Answer: The portion the bowling pins did you knockdown is: \(\frac{5}{10}\) = 0.6
Explanation:
It is given that you knock down 5 bowling pins out of 10 bowling pins.
So,
The representation of the portion of bowling pins you knock down is: \(\frac{5}{10}\)
so,
The representation of \(\frac{5}{10}\) in the place-value chart is:
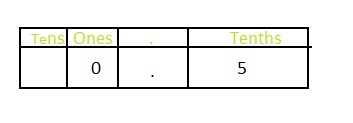
In \(\frac{5}{10}\),
5 represents the tenth’s position
Hence,
The representation of the portion of the bowling pins that you knockdown in the decimal form is: \(\frac{5}{10}\) = 0.5
Question 14.
You drive a go-kart around a track 8\(\frac{7}{10}\) times before you spin out. Write this number as a decimal.

Answer: The representation of 8\(\frac{7}{10}\) in the decimal form is: 8.7
Explanation:
It is given that you drive a go-kart around a track 8\(\frac{7}{10}\) before you spin out.
So,
The given mixed fraction is: 8\(\frac{7}{10}\)
So,
The improper fraction of 8\(\frac{7}{10}\) is: \(\frac{87}{10}\)
So,
The representation of 8\(\frac{7}{10}\) in the place-value chart is:
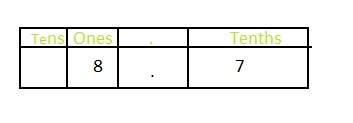
In 8\(\frac{7}{10}\),
8 represents the one’s position
7 represents the tenth’s position
Hence,
The representation of 8\(\frac{7}{10}\) in the decimal form is: 8.7
Question 15.
DIG DEEPER!
Which number-cards are represented by the model?
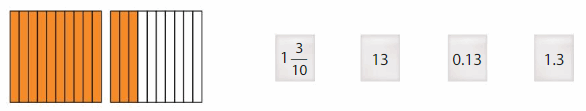
Use the table.
Answer: The number- cards represented by the model are: 1\(\frac{3}{10}\) and 1.3
Explanation:
The given model is:
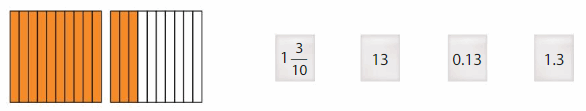
In the given model, the tables are represented by:
A) 1\(\frac{3}{10}\) B) 13 C) 0.13 D) 1.3
In the given model,
Consider the fully colored model as one whole unit.
So,
The total number of colored units is: 10
Now, in another model,
The number of colored parts is: 3
The number of total parts is: 10
So,
The portion of the colored part from the total number of parts is: \(\frac{3}{10}\)
So, by combining the 2 models,
The total number of colored parts = 1 + \(\frac{3}{10}\)
= 1 + 0.3
= 1.3
So,
The representation of the total number of colored parts in the mixed fraction form is: 1\(\frac{3}{10}\)
The representation of the total number of colored parts in the decimal form is: 1.3
Question 16.
Modeling Real Life
A photographer frames her photographs from a safari trip. What portion of the framed photographs are of mammals? Write your answer as a decimal.
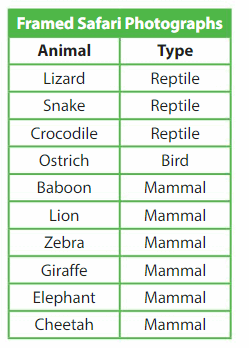

Answer: The portion of the framed photographs that are of mammals in the decimal form is: 0.6
Explanation:
It is given that a photographer frames photos from a safari trip and the framed photos are all categorized according to the table given below:

So,
From the table,
The total number of framed photographs are: 10
The number of framed photographs that are mammals is: 6
So,
The portion of the mammals from the total number of framed photographs in the fraction form is: \(\frac{6}{10}\)
The representation of the \(\frac{6}{10}\) in the place-value chart is:
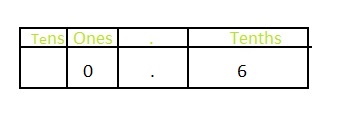
In \(\frac{6}{10}\),
6 represents the tenth’s position
Hence,
The portion of the mammals from the framed photographs in the decimal form is: 0.6
Question 17.
DIG DEEPER!
What portion of the framed not photographs are of mammals? Write your answer as a decimal.
Answer: THe portion of the photographs that are not mammals in the decimal form is: 0.4
Explanation:
The table for all the framed photographs is given below:

From the table,
The total number of framed photographs are: 10
The number of framed photographs that are not mammals is: 4
So,
The portion of the photographs that are not mammals in the fraction form is: \(\frac{4}{10}\)
The representation of \(\frac{4}{10}\) in the place-value chart is:
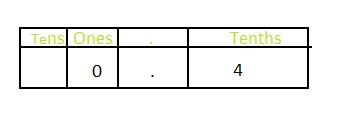
In \(\frac{4}{10}\),
4 represents the tenth’s position
Hence,
The number of framed photographs that are not mammals in the decimal form is: 0.4
Review & Refresh
Find the product.
Question 18.
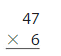
Answer: 47 × 6 = 282
Explanation:
By using the partial products method,
47 × 6 = ( 40 + 7 ) × 6
= ( 40 × 6 ) + ( 7 × 6 )
= 240 + 42
= 282
Hence, 47 × 6 = 282
Question 19.

Answer: 961 × 3 = 2,883
Explanation:
By using the partial products method,
961 × 3 = ( 900 + 60 + 1 ) × 3
= ( 900 × 3 ) + ( 60 × 3 ) + ( 1 × 3 )
= 2,700 + 180 + 3
= 2,883
Hence, 961 × 3 = 2,883
Question 20.
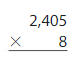
Answer: 2,405 × 8 = 19,240
Explanation:
By using the partial products method,
2,405 × 8 = ( 2,400 + 5 ) × 8
= ( 2,400 × 8 ) + ( 5 × 8 )
= 19,200 + 40
= 19,240
Hence, 2,405 × 8 = 19,240
Lesson 10.2 Understand Hundredths
Explore and Grow
How many pennies have a total value of one dollar? Draw a model.

One penny is what fraction of one dollar? Write your answer in words and as a fraction.
Answer: The representation of one penny into the dollar in the fraction form is: 0.01
Explanation:
The given note is:

We know that,
1 Dollar = 100 pennies
So,
The representation of 1 penny into the dollar is: \(\frac{1}{100}\) dollars

Hence, one dollar is equal to 100 pennies and 1 penny is equal to 0.01 dollars
Structure
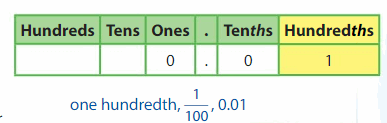
How is one-tenth related to one hundredth? How do you think you can write \(\frac{1}{100}\) in a place value chart?
Answer: The one-tenth is related to the one-hundredth as: \(\frac{1}{10}\)
Explanation:
We know that,
one-hundredth = \(\frac{1}{10}\) × \(\frac{1}{10}\)
Now,
The representation of \(\frac{1}{100}\) in the place-value chart is:
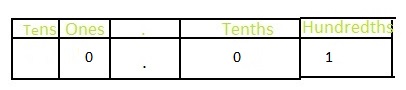
In \(\frac{1}{100}\),
1 represents the hundredth’s position
Think and Grow: Understand Hundredths
In decimal, the second place to the right of the decimal point is the hundredths place. You can write hundredths as fractions or decimals. A fraction with a denominator of 10 or 100 is called a decimal fraction.
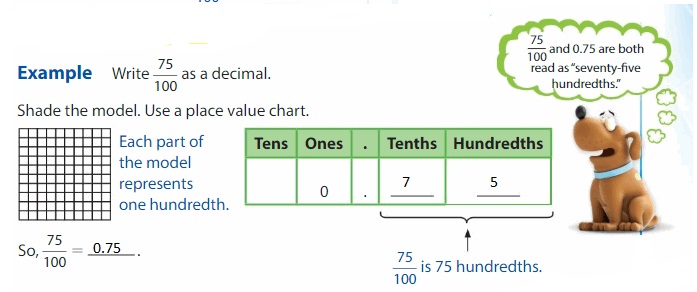
Show and Grow
Write the fraction or mixed number as a decimal.
Question 1.

Answer: The representation of \(\frac{45}{100}\) in the decimal form is: 0.45
Explanation:
The given fraction is: \(\frac{45}{100}\)
The model given for \(\frac{45}{100}\) is:

So,
The representation of \(\frac{45}{100}\) in the place-value chart is:

In \(\frac{45}{100}\),
5 represents the hundredth’s position
4 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{45}{100}\) in the decimal form is: 0.45
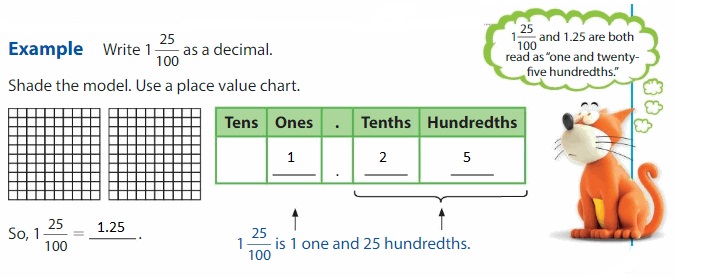
Question 2.

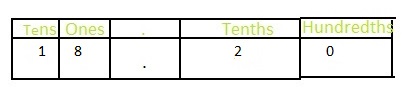
Answer: The representation of 1\(\frac{90}{100}\) in the decimal form is: 1.90
Explanation:
The given fraction is: 1\(\frac{90}{100}\)
The model given for 1\(\frac{90}{100}\) is:

So,
The representation of 1\(\frac{90}{100}\) in the place-value chart is:
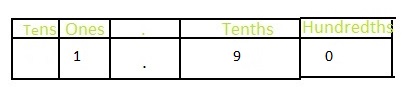
In 1\(\frac{90}{100}\),
1 represents the one’s position
0 represents the hundredth’s position
9 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 1\(\frac{90}{100}\) in the decimal form is: 1.90
Apply and Grow: Practice
Shade the model to represent the fraction or mixed number. Then write the fraction or mixed number as a decimal.
Question 3.

Answer: The representation of \(\frac{98}{100}\) in the decimal form is: 0.98
Explanation:
The given fraction is: \(\frac{98}{100}\)
The model given for \(\frac{98}{100}\) is:

So,
The representation of \(\frac{98}{100}\) in the place-value chart is:
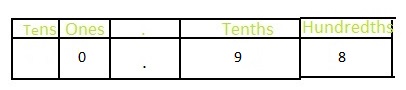
In \(\frac{98}{100}\),
8 represents the hundredth’s position
9 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{98}{100}\) in the decimal form is: 0.98
Question 4.

Answer:
The representation of 1\(\frac{34}{100}\) in the decimal form is: 1.34
Explanation:
The given mixed fraction is: 1\(\frac{34}{100}\)
So,
The improper fraction of 1\(\frac{34}{100}\) is: \(\frac{134}{100}\)
The model given for 1\(\frac{34}{100}\) is:

So,
The representation of 1\(\frac{34}{100}\) in the place-value chart is:
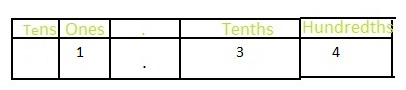
In 1\(\frac{34}{100}\),
1 represents the one’s position
4 represents the hundredth’s position
3 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 1\(\frac{34}{100}\) in the decimal form is: 1.34
Write the fraction or mixed number as a decimal.
Question 5.
\(\frac{42}{100}\)
Answer: The representation of \(\frac{42}{100}\) in the form of decimal number is: 0.42
Explanation:
The given fraction is: \(\frac{42}{100}\)
Now,
The representation of \(\frac{42}{100}\) in the place-value chart is:
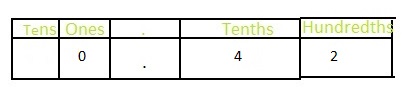
In \(\frac{42}{100}\),
2 represents the hundredth position
4 represents the tenth position
Hence,
The representation of \(\frac{42}{100}\) in the decimal form is: 0.42
Question 6.
\(\frac{7}{100}\)
Answer: The representation of \(\frac{7}{100}\) in the form of decimal number is: 0.07
Explanation:
The given fraction is: \(\frac{7}{100}\)
Now,
The representation of \(\frac{7}{100}\) in the place-value chart is:
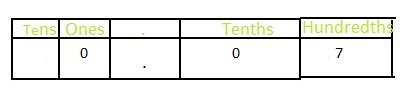
In \(\frac{7}{100}\),
7 represents the hundredth position
0 represents the tenth position
Hence,
The representation of \(\frac{7}{100}\) in the decimal form is: 0.07
Question 7.
4\(\frac{56}{100}\)
Answer: The representation of 4\(\frac{56}{100}\) in the form of a decimal number is: 4.56
Explanation:
The given mixed fraction is: 4\(\frac{56}{100}\)
So,
The improper fraction of 4\(\frac{56}{100}\) is: \(\frac{456}{100}\)
Now,
The representation of 4\(\frac{56}{100}\) in the place-value chart is:
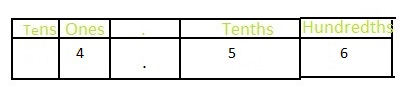
In 4\(\frac{56}{100}\),
4 represents the one’s position
6 represents the hundredth position
5 represents the tenth position
Hence,
The representation of 4\(\frac{56}{100}\) in the decimal form is: 4.56
Question 8.
23\(\frac{9}{100}\)
Answer: The representation of 23\(\frac{9}{100}\) in the form of a decimal number is: 23.09
Explanation:
The given mixed fraction is: 23\(\frac{9}{100}\)
So,
The improper fraction of 23\(\frac{9}{100}\) is: \(\frac{2,309}{100}\)
Now,
The representation of 23\(\frac{9}{100}\) in the place-value chart is:

In 23\(\frac{9}{100}\),
2 represents the ten’s position
3 represents the one’s position
9 represents the hundredth position
0 represents the tenth position
Hence,
The representation of 23\(\frac{9}{100}\) in the decimal form is: 23.09
Write the fraction or mixed number as a decimal.
Question 9.
sixty-one hundredths
Answer:
The representation of sixty-one hundredths in the fraction form is: \(\frac{61}{100}\)
The representation of sixty-one hundredths in the decimal form is: 0.61
Explanation:
The given word form is: Sixty-one hundredths
So,
The representation of sixty-one hundredths in the fraction form is: \(\frac{61}{100}\)
Now,
The representation of \(\frac{61}{100}\) in the place-value chart is:
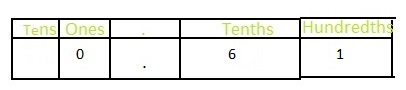
In \(\frac{61}{100}\),
1 represents the hundredth’s position
6 represents the tenth’s position
Hence,
The representation of \(\frac{61}{100}\) in the decimal form is: 0.61
Question 10.
twelve and eighty-three hundredths
Answer:
The representation of twelve and eighty-three hundredths in the fraction form is: 12\(\frac{83}{100}\)
The representation of twelve and eighty-three hundredths in the decimal form is: 12.83
Explanation:
The given word form is: twelve and eighty-three hundredths
So,
The representation of twelve and eighty-three hundredths in the fraction form is: 12\(\frac{83}{100}\)
Now,
The representation of 12\(\frac{83}{100}\) in the place-value chart is:

In 12\(\frac{83}{100}\),
1 represents the ten’s position
2 represents the one’s position
3 represents the hundredth’s position
8 represents the tenth’s position
Hence,
The representation of 12\(\frac{83}{100}\) in the decimal form is: 12.83
Question 11.
A shelter finds homes for 100 dogs. Five of the dogs are Doberman pinschers. What portion of the dogs are Doberman pinschers? Write your answer as a decimal.

Answer: The portion of the dogs that are Doberman pinschers in the fraction form is: 0.05
Explanation:
It is given that a shelter finds homes for 100 dogs and out of these 100 dogs, 5 dogs are Doberman pinschers
So,
The portion of the dogs that are Doberman pinschers = \(\frac{The number of dogs that are Doberman pinschers}{The total number of dogs}\)
= \(\frac{5}{100}\)
So,
The representation of \(\frac{5}{100}\) in the place-value chart is:

In \(\frac{5}{100}\),
0 represents the tenth’s position
5 represents the hundredth’s position
Hence,
The portion of the dogs that are Doberman pinschers in the decimal form is: 0.05
Question 12.
An athlete runs 3\(\frac{50}{100}\) lengths of a football field. Write this number as a decimal.

Answer: The representation of 3\(\frac{50}{100}\) in the decimal form is: 3.5
Explanation:
It is given that an athlete runs 3\(\frac{50}{100}\) lengths of a football field.
So,
The representation of 3\(\frac{50}{100}\) in the place-value chart is:
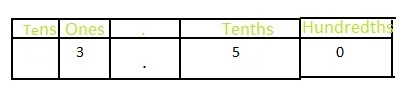
Now,
In 3\(\frac{50}{100}\),
3 represents the one’s place
0 represents the hundredth’s place
5 represents the tenth’s position
Now,
The given mixed fraction is: 3\(\frac{50}{100}\)
So,
The improper fraction of 3\(\frac{50}{100}\) is: \(\frac{350}{100}\)
So,
The representation of 3\(\frac{50}{100}\) in the decimal form is: 3.50
Question 13.
Number Sense
Which number of cards show three-hundredths?

Answer: From the given cards, \(\frac{3}{100}\) and 0.03 shows the form of three-hundredths
Explanation:
The given number of cards is:

The given fractions and decimal numbers in the given table are:
A) \(\frac{3}{100}\) B) \(\frac{3}{10}\) C) 300 D) 0.3 E) 0.03
We can observe that
From three-hundredths, we can say that,
The total number of cards are: 100
The portion of cards from 100 cards is: 3
So,
The representation of three-hundredths in the fraction form is: \(\frac{3}{100}\)
Now,
The representation of \(\frac{3}{100}\) in the place-value chart is:

In \(\frac{3}{100}\),
0 represents the tenth’s position
3 represents the hundredth’s position
So,
The representation of \(\frac{3}{100}\) in the decimal form is: 0.03
hence, from the given table,
We can conclude that the number of cards that represent the three-hundredths is: \(\frac{3}{100}\) and 0.03
Think and Grow: Modeling Real Life
Example
You use 51 toothpicks to make a bridge. What portion of the container of toothpicks do you use to make the bridge? Write your answer as a decimal.
Draw a model to represent the container of toothpicks. Shade the same number of parts as the number of toothpicks you use to make the bridge. Write the decimal shown by the model
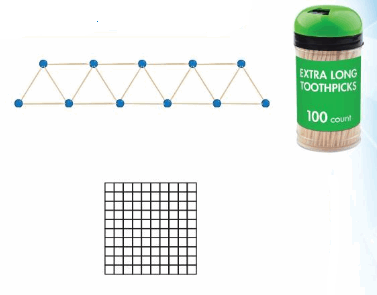
Answer:
It is given that you are using 51 toothpicks to make a bridge.
So,
The total number of chopsticks are: 100
The number of chopsticks that are using to make a bridge is: 51
So,
The representation of the portion of the chopsticks that are used to make chopsticks = \(\frac{51}{100}\)
So, from \(\frac{3}{100}\),
We can say that you use 51 of the container of toothpicks to make the bridge.
Show and Grow
Question 14.
A book fair has 100 books. 60 of the books are chapter books. What portion of the books in the book fair are chapter books? Write your answer as a decimal.
Answer: The portion of the chapter books out of the total number of books in the decimal form is: 0.60
Explanation:
It is given that a book fair has 100 books and out of these 100 books, 60 books are chapter books.
So,
The portion of the chapter books out of the total number of books in the fraction form is: \(\frac{60}{100}\)
Now,
The representation of \(\frac{60}{100}\) in the place-value chart is:
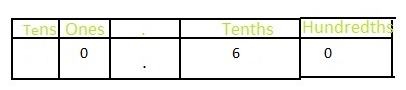
From \(\frac{60}{100}\), we can say that
0 represents the hundredth’s position-
6 represents the tenth’s position
So,
The representation of \(\frac{60}{100}\) in the decimal form is: 0.60
Hence, from the above,
We can conclude that the portion of the books that are the chapter books in the decimal form is: 0.60
Question 15.
The model represents the members of a marching band. What portion of the marching band plays a brass instrument? percussion instrument? Write your answers as decimals.
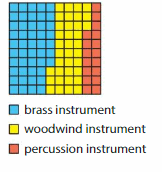
Answer: The portion of the marching band that plays a brass instrument is: 0.47
Explanation:
It is given that the below model represents the members of a marching band.
The given model is:

In the given model, there are 3 categories of marching brand
In the given model, each box represents 1 unit.
So,
From the model,
The number of the marching band that plays a brass instrument is: 47
The number of the marching band that plays a woodwind instrument is: 36
The number of the marching band that plays a percussion instrument is: 17
The total number of instruments are: 100
So,
The portion of the marching band that plays a band instrument from the total number of instruments in the fraction form is: \(\frac{47}{100}\)
Hence, from the above,
The portion of the marching band that plays a band instrument from the total number of instruments i the decimal form is: 0.47
Question 16.
DIG DEEPER!
What portion of Earth’s surface is covered by water? Write your answer as a decimal.

Answer: The portion of Earth’s surface that is covered by water in the fraction form is: 0.71
Explanation:
It is given that about \(\frac{71}{100}\) of earth’s surface is covered by water.
So,
The representation of \(\frac{71}{100}\) in the place-value chart is:
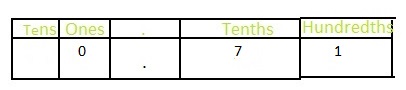
From \(\frac{71}{100}\), we can say that
1 represents the hundredth’s position
7 represents the tenth’s position
Hence,
The portion of water on the Earth’s surface represented in decimal form is: 0.71
Understand Hundredths Homework & Practice 10.2
Write the fraction or mixed number as a decimal.
Question 1.
Write \(\frac{83}{100}\) as a decimal.

Answer: The representation of \(\frac{83}{100}\) in the decimal form is: 0.98
Explanation:
The given fraction is: \(\frac{83}{100}\)
The model given for \(\frac{83}{100}\) is:

So,
The representation of \(\frac{83}{100}\) in the place-value chart is:
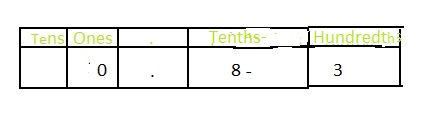
In \(\frac{83}{100}\),
3 represents the hundredth’s position
8 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{83}{100}\) in the decimal form is: 0.83
Question 2.
Shade the model to represent 1\(\frac{65}{100}\). Then write the mixed number as a decimal.

Answer: The representation of \(\frac{65}{100}\) in the form of a decimal number is: 1.65
Explanation:
The given mixed fraction is: 1\(\frac{65}{100}\)
So,
The improper fraction of 1\(\frac{65}{100}\) is: \(\frac{165}{100}\)
Now,
The representation of 1\(\frac{65}{100}\) in the place-value chart is:
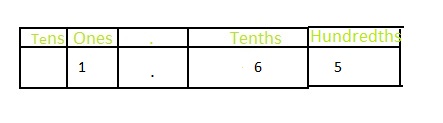
In 1\(\frac{65}{100}\),
1 represents the one’s position
5 represents the hundredth position
6 represents the tenth position
Hence,
The representation of 1\(\frac{65}{100}\) in the decimal form is: 1.65
Question 3.
\(\frac{12}{100}\)
Answer: The representation of \(\frac{12}{100}\) in the decimal form is: 0.12
Explanation:
The given fraction is: \(\frac{12}{100}\)
So,
The representation of \(\frac{12}{100}\) in the place-value chart is:
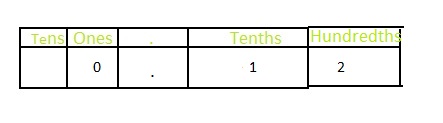
In \(\frac{12}{100}\),
2 represents the hundredth’s position
1 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{12}{100}\) in the decimal form is: 0.12
Question 4.
\(\frac{24}{100}\)
Answer: The representation of \(\frac{24}{100}\) in the decimal form is: 0.24
Explanation:
The given fraction is: \(\frac{24}{100}\)
So,
The representation of \(\frac{24}{100}\) in the place-value chart is:
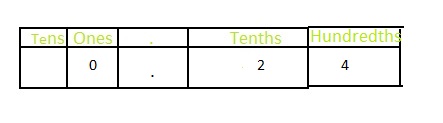
In \(\frac{24}{100}\),
4 represents the hundredth’s position
2 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{24}{100}\) in the decimal form is: 0.24
Question 5.
\(\frac{2}{100}\)
Answer: The representation of \(\frac{2}{100}\) in the decimal form is: 0.02
Explanation:
The given fraction is: \(\frac{2}{100}\)
So,
The representation of \(\frac{2}{100}\) in the place-value chart is:
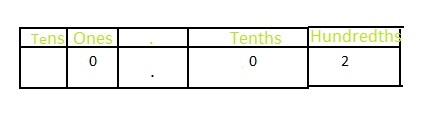
In \(\frac{2}{100}\),
2 represents the hundredth’s position
0 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{2}{100}\) in the decimal form is: 0.02
Question 6.
\(\frac{8}{100}\)
Answer: The representation of \(\frac{8}{100}\) in the decimal form is: 0.08
Explanation:
The given fraction is: \(\frac{8}{100}\)
So,
The representation of \(\frac{8}{100}\) in the place-value chart is:
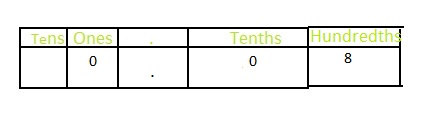
In \(\frac{8}{100}\),
8 represents the hundredth’s position
0 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{8}{100}\) in the decimal form is: 0.08
Question 7.
2\(\frac{59}{100}\)
Answer: The representation of 2\(\frac{59}{100}\) in the form of a decimal number is: 2.59
Explanation:
The given mixed fraction is: 2\(\frac{59}{100}\)
So,
The improper fraction of 2\(\frac{59}{100}\) is: \(\frac{259}{100}\)
Now,
The representation of 2\(\frac{59}{100}\) in the place-value chart is:
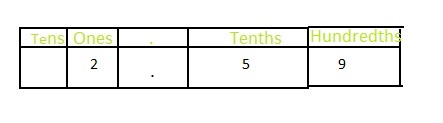
In 2\(\frac{59}{100}\),
2 represents the one’s position
9 represents the hundredth position
5 represents the tenth position
Hence,
The representation of 2\(\frac{59}{100}\) in the decimal form is: 2.59
Question 8.
48\(\frac{31}{100}\)
Answer: The representation of 48\(\frac{31}{100}\) in the form of a decimal number is: 48.31
Explanation:
The given mixed fraction is: 48\(\frac{31}{100}\)
So,
The improper fraction of 48\(\frac{31}{100}\) is: \(\frac{4,831}{100}\)
Now,
The representation of 48\(\frac{31}{100}\) in the place-value chart is:
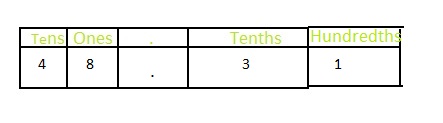
In 48\(\frac{31}{100}\),
4 represents ten’s position
8 represents the one’s position
1 represents the hundredth position
3 represents the tenth position
Hence,
The representation of 48\(\frac{31}{100}\) in the decimal form is: 48.31
Question 9.
6\(\frac{7}{100}\)
Answer: The representation of 6\(\frac{7}{100}\) in the form of a decimal number is: 6.07
Explanation:
The given mixed fraction is: 6\(\frac{7}{100}\)
So,
The improper fraction of 6\(\frac{7}{100}\) is: \(\frac{607}{100}\)
Now,
The representation of 6\(\frac{7}{100}\) in the place-value chart is:
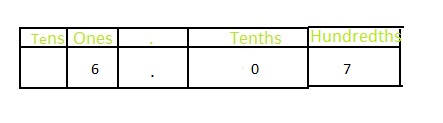
In 6\(\frac{7}{100}\),
6 represents the one’s position
7 represents the hundredth position
0 represents the tenth position
Hence,
The representation of 6\(\frac{7}{100}\) in the decimal form is: 6.07
Question 10.
31\(\frac{6}{100}\)
Answer: The representation of 31\(\frac{6}{100}\) in the form of a decimal number is: 31.06
Explanation:
The given mixed fraction is: 31\(\frac{6}{100}\)
So,
The improper fraction of 31\(\frac{6}{100}\) is: \(\frac{3,106}{100}\)
Now,
The representation of 31\(\frac{6}{100}\) in the place-value chart is:
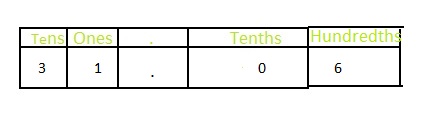
In 31\(\frac{6}{100}\),
3 represents the ten’s position
1 represents the one’s position
6 represents the hundredth position
0 represents the tenth position
Hence,
The representation of 31\(\frac{6}{100}\) in the decimal form is: 31.06
Write the number as a fraction or mixed number and as a decimal.
Question 11.
seventy-four hundredths
Answer:
The representation of seventy-four hundredths in the fraction form is: \(\frac{74}{100}\)
The representation of seventy-four hundredths in the decimal form is: 0.74
Explanation:
The given word form is: Seventy-four hundredths
So,
The representation of seventy-four hundredths in the fraction form is: \(\frac{74}{100}\)
Now,
The representation of \(\frac{74}{100}\) in the place-value chart is:
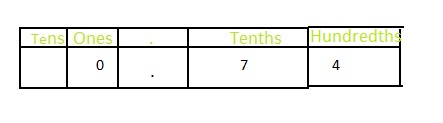
In \(\frac{74}{100}\),
4 represents the hundredth’s position
7 represents the tenth’s position
Hence,
The representation of \(\frac{74}{100}\) in the decimal form is: 0.74
Question 12.
sixteen and thirty-one hundredths
Answer:
The representation of sixteen and thirty-one hundredths in the fraction form is: 16\(\frac{31}{100}\)
The representation of sixteen and thirty-one hundredths in the decimal form is: 16.31
Explanation:
The given word form is: sixteen and thirty-one hundredths
So,
The representation of sixteen and thirty-one hundredths in the fraction form is: 16\(\frac{31}{100}\)
Now,
The representation of 16\(\frac{31}{100}\) in the place-value chart is:
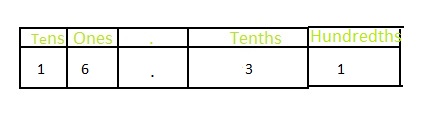
In 16\(\frac{31}{100}\),
1 represents the ten’s position
6 represents the one’s position
1 represents the hundredth’s position
3 represents the tenth’s position
Hence,
The representation of 16\(\frac{31}{100}\) in the decimal form is: 16.31
Write the value of the underlined digit.
Question 13.
5.84
Answer: The value of 8 in 5.84 is: 0.8
Explanation:
The given number is: 5.84
The representation of 5.84 in the place-value chart is:
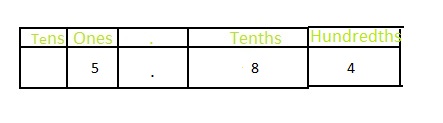
In 5.83, from the place-value chart,
We can say that the value of 8 in 5.83 is: 0.8
Question 14.
21.03
Answer: The value of 2 in 21.03 is: 20
Explanation:
The given number is: 21.03
The representation of 21.03 in the place-value chart is:
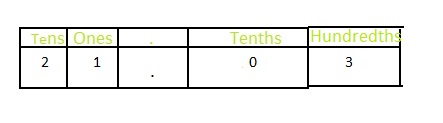
From the above place-value chart,
We can say that the value of 2 in 21.03 is: 20
Question 15.
67.32
Answer: The value of 2 in 67.32 is: 0.02
Explanation:
The given number is: 67.32
The representation of 67.32 in the place-value chart is:
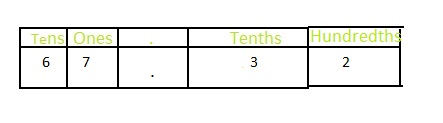
From the above place-value chart,
We can say that the value of 2 in 67.32 is: 0.02
Question 16.
506.19
Answer: The value of 5 in 506.19 is: 500
Explanation:
The given number is: 506.19
The representation of 506.19 in the place-value chart is:

From the above place-value chart,
We can say that the value of 5 in 506.19 is: 500
Question 17.
A clown has 100 balloons. She uses 56 of the balloons to make animals. What portion of the balloons does she use? Write your answer as a decimal.

Answer: The portion of the balloons she used to make animals in the decimal form is: 0.56
Explanation:
It is given that a clown has 100 balloons and she uses 56 of the balloons to make animals.
So,
The total number of balloons are: 100
The number of ballons that are used to make animals is: 56
So,
The portion of the balloons that are used to make animals is:\(\frac{56}{100}\)
So,
The representation of \(\frac{56}{100}\) in the place-value chart is:
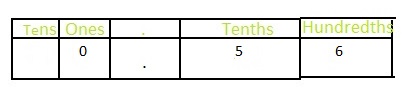
Hence,
We can conclude that the portion of the balloons that are used to make animals in the decimal form is: 0.56
Question 18.
You fill a beaker 4\(\frac{35}{100}\) times for an experiment. Write this number as a decimal.

Answer: The representation of 4\(\frac{35}{100}\) in the form of a decimal number is: 4.35
Explanation:
The given mixed fraction is: 4\(\frac{35}{100}\)
So,
The improper fraction of 4\(\frac{35}{100}\) is: \(\frac{435}{100}\)
Now,
The representation of 4\(\frac{35}{100}\) in the place-value chart is:

In 4\(\frac{35}{100}\),
4 represents the one’s position
5 represents the hundredth position
3 represents the tenth position
Hence,
The representation of 4\(\frac{35}{100}\) in the decimal form is: 4.35
Question 19.
YOU BE THE TEACHER
Descartes writes 2\(\frac{40}{100}\) as 2.04. Is he correct? Explain.
Answer:
The representation of 2\(\frac{40}{100}\) in the form of a decimal number is: 2.40
So, Descartes is wrong.
Explanation:
The given mixed fraction is: 2\(\frac{40}{100}\)
So,
The improper fraction of 2\(\frac{40}{100}\) is: \(\frac{240}{100}\)
Now,
The representation of 2\(\frac{40}{100}\) in the place-value chart is:
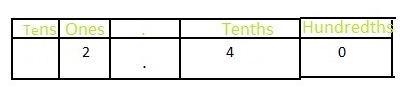
In 2\(\frac{40}{100}\),
2 represents the one’s position
0 represents the hundredth position
4 represents the tenth position
So,
The representation of 2\(\frac{40}{100}\) in the decimal form is: 2.40
But, according to Descartes,
The representation of 2\(\frac{40}{100}\) in the decimal form is: 2.04
Hence, from the above,
We can conclude that Descartes is not correct.
Question 20.
DIG DEEPER!
Shade each model to show 0.6 and 0.60. What do you notice?
Answer: From the values of 0.6 and 0.60, we can notice that the value of 6 in both numbers are the same.
Explanation:
The given numbers are: 0.6 and 0.60
The given models of 0.6 and 0.60 are:

Now,
The shaded models of 0.6 and 0.60 will be:
Now,
The representation of 0.6 in the place-value chart is:
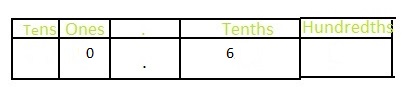
The representation of 0.60 in the place-value chart is:
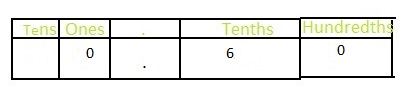
Hence,
From the above 2 place-value charts,
We can conclude that 0.6 and 0.60 are the same as the value of 6 in 0.6 and 0.60 is the same.
Question 21.
Modeling Real Life
You work on the puzzle shown. You connect 78 of the puzzle pieces. What portion of the puzzle have you completed? Write your answer as a decimal.

Answer: The portion of the puzzles you have completed in the decimal form is: 0.78
Explanation:
It is given that you are working on a 100-box puzzle and you connected 78 of the puzzle pieces.
So,
The total number of puzzles are: 100
The number of puzzles that are connected is: 78
So,
The portion of the puzzles that are connected in the fraction form is: \(\frac{78}{100}\)
Now,
The representation of \(\frac{78}{100}\) in the place-value chart is:
Hence, from the above,
We can conclude that the portion of the puzzles that are connected in the decimal form is: 0.78
Review & Refresh
Divide. Then check your answer.
Question 22.
![]()
Answer: 1,308 ÷ 5 = 261 R 3
Explanation:
By using the partial quotients method,
1,308 ÷ 5 = ( 1,000 + 300 + 5 ) ÷ 5
= ( 1,000 ÷ 5 ) + ( 300 ÷ 5 ) + ( 5 ÷ 5 )
= 200 + 60 + 1
= 261 R 3
Hence, 1,308 ÷ 5 = 261 R 3
Question 23.
![]()
Answer: 67 ÷ 4 = 16 R 3
Explanation:
By using the partial quotients method,
67 ÷ 4 = ( 56 + 8 ) ÷ 4
= ( 56 ÷ 4 ) + ( 8 ÷ 4 )
= 14 + 2
= 16 R 3
Henec, 67 ÷ 4 = 1 R 3
Question 24.
![]()
Answer: 725 ÷ 2 = 362 R 1
Explanation:
By using the partial quotients method,
725 ÷ 2 = ( 720 + 4 ) ÷ 2
= ( 720 ÷ 2 ) + ( 4 ÷ 2 )
= 360 + 2
= 362 R 1
Hence,
75 ÷ 2 = 362 R 1
Lesson 10.3 Fractions and Decimals
Explore and Grow
Plot each fraction or decimal on a number line.
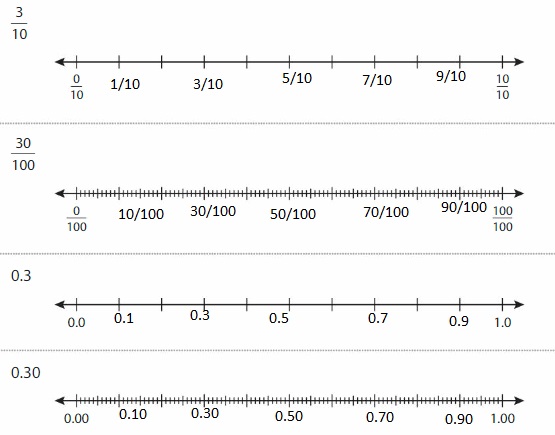
Reasoning
What do you notice about the locations of the points? What can you conclude about the numbers?
Answer: From the above plots, we can see that the number of lines between any two numbers is the same whether the given number is in fraction form or in the decimal form
So, from the above plots, we can conclude that the location of the numbers and the gap between the two numbers is the same.
Think and Grow: Fractions and Decimals
Example
Write \(\frac{6}{10}\) as hundredths in fraction form and decimal form.
Fraction form: Shade the model to help write \(\frac{6}{10}\) as an equivalent fraction with a denominator of 100.
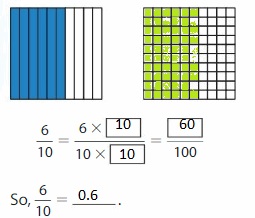

Two or more decimals that have the same value are equivalent decimals.
Example
Write 0.40 as tenths in decimal form and fraction form.


Show and Grow
Question 1.
Write \(\frac{9}{10}\) as hundredths in fraction form and decimal form.
Answer:
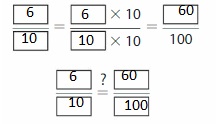
The representation of \(\frac{9}{10}\) as hundredths in the fraction form is: \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal form is: 0.90
Explanation:
The given fraction is: \(\frac{9}{10}\)
So, to write \(\frac{9}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{9}{10}\) with 10.
So,
Firstly the numerators 9 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{90}{100}\) in the place-value chart is:
Hence,
The representation of \(\frac{9}{10}\) as hundredths in the fraction form is: \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal form is: 0.90
Question 2.
Write 0.20 as tenths in decimal form and fraction form.
Answer:
The representation of 0.20 as tenths in the fraction form is: \(\frac{2}{10}\)
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Explanation:
The given fraction is: \(\frac{20}{100}\)
So, to write \(\frac{20}{100}\) as tenths, divide the fraction and numerator of \(\frac{20}{100}\) with 10.
So,
Firstly the numerators 20 and 10 are divided and then the denominators 100 and 10 are divided
So,
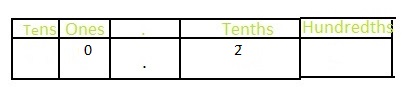
\(\frac{20}{100}=\frac{20 \div 10}{100 \div 10}=\frac{2}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{2}{10}\) in the place-value chart is:
Hence,
The representation of \(\frac{20}{100}\) as tenths in the fraction form is: \(\frac{2}{10}\)
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Apply and Grow: Practice
Write the number as tenths in fraction form and decimal form.
Question 3.
\(\frac{80}{100}\)
Answer:
The representation of \(\frac{80}{100}\) as tenths in the fraction form is: \(\frac{8}{10}\)
The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Explanation:
The given fraction is: \(\frac{80}{100}\)
So, to write \(\frac{80}{100}\) as tenths, divide the fraction and numerator of \(\frac{80}{100}\) with 10.
So,
Firstly the numerators 80 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{80}{100}=\frac{80 \div 10}{100 \div 10}=\frac{8}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{80}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{80}{100}\) as tenths in the fraction form is: \(\frac{8}{10}\)
The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Question 4.
\(\frac{50}{100}\)
Answer:
The representation of \(\frac{50}{100}\) as tenths in the fraction form is: \(\frac{5}{10}\)
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Explanation:
The given fraction is: \(\frac{50}{100}\)
So, to write \(\frac{50}{100}\) as tenths, divide the fraction and numerator of \(\frac{50}{100}\) with 10.
So,
Firstly the numerators 50 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{50}{100}=\frac{50 \div 10}{100 \div 10}=\frac{5}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{50}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{50}{100}\) as tenths in the fraction form is: \(\frac{5}{10}\)
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Question 5.
0.30
Answer:
The representation of 0.30 as tenths in the fraction form is: \(\frac{3}{10}\)
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Explanation:
The given decimal number is: 0.30
So,
The representation of 0.30 in the fraction form is: \(\frac{30}{100}\)
So, to write \(\frac{30}{100}\) as tenths, divide the fraction and numerator of \(\frac{30}{100}\) with 10.
So,
Firstly the numerators 30 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{30}{100}=\frac{30 \div 10}{100 \div 10}=\frac{3}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{3}{10}\) in the place-value chart is:

Hence,
The representation of \(\frac{30}{100}\) as tenths in the fraction form is: \(\frac{3}{10}\)
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Write the number as hundredths in fraction form and decimal form.
Question 6.
\(\frac{2}{10}\)
Answer:
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
The representation of \(\frac{20}{100}\) in the decimal form is: 0.20
Explanation:
The given fraction is: \(\frac{2}{10}\)
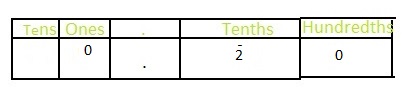
So, to write \(\frac{2}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{2}{10}\) with 10.
So,
Firstly the numerators 2 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{20}{100}\) in the place-value chart is:
Hence,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
The representation of \(\frac{20}{100}\) in the decimal form is: 0.20
Question 7.
0.7
Answer:
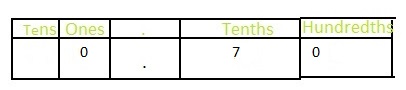
The representation of 0.7 as hundredths in the fraction form is: \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
Explanation:
The given decimal number is: 0.7
So,
The representation of 0.7 in the fraction form is: \(\frac{7}{10}\)
So, to write \(\frac{7}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{7}{10}\) with 10.
So,
Firstly the numerators 7 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{70}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
Question 8.
2\(\frac{1}{10}\)
Answer:
The representation of 2\(\frac{1}{10}\) as hundredths in the fraction form is: 2\(\frac{10}{100}\)
The representation of 2\(\frac{10}{100}\) in the decimal form is: 2.10
Explanation:
The given mixed fraction is: 2\(\frac{1}{10}\)
So,
To write 2\(\frac{1}{10}\) as hundredths, multiply the fraction and numerator of 2\(\frac{1}{10}\) with 10.
So,
Firstly the numerators 1 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of 2\(\frac{10}{100}\) in the place-value chart is:
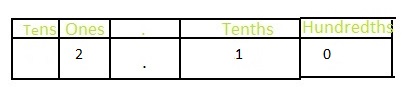
Hence,
The representation of 2\(\frac{1}{10}\) as hundredths in the fraction form is: 2\(\frac{10}{100}\)
The representation of 2\(\frac{10}{100}\) in the decimal form is: 2.10
Write the number represented by the point as hundredths in fraction form and decimal form.

Answer:
From the above number line,
‘A’ is: 0.4
‘B’ is: 0.9
‘C’ is: 1.5
Question 9.
A
Answer:
From the above number line, ‘A’ is: 0.4
The representation of 0.4 as hundredths in the fraction form is: \(\frac{40}{100}\)
The representation of \(\frac{40}{100}\) in the decimal form is: 0.40
Explanation:
The given decimal number is: 0.4
So,
The representation of 0.4 in the fraction form is: \(\frac{4}{10}\)
So,
To write \(\frac{4}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{4}{10}\) with 10.
So,
Firstly the numerators 4 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{40}{100}\) in the place-value chart is:
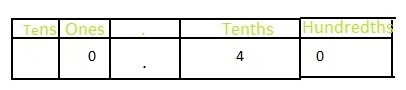
Hence,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
The representation of \(\frac{40}{100}\) in the decimal form is: 0.40
Question 10.
B
Answer:
From the above number line, ‘B’ is: 0.9
The representation of 0.9 as hundredths in the fraction form is: \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal form is: 0.90
Explanation:
The given decimal number is: 0.9
So,
The representation of 0.9 in the fraction form is: \(\frac{9}{10}\)
So,
To write \(\frac{9}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{9}{10}\) with 10.
So,
Firstly the numerators 9 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{90}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{9}{10}\) as hundredths in the fraction form is: \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal form is: 0.90
Question 11.
C
Answer:
From the above number line, ‘C’ is: 1.5
The representation of 1.5 as hundredths in the fraction form is: \(\frac{150}{100}\)
The representation of \(\frac{150}{100}\) in the decimal form is: 1.50
Explanation:
The given decimal number is: 1.5
So,
The representation of 1.5 in the fraction form is: \(\frac{15}{10}\)
So,
To write \(\frac{15}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{15}{10}\) with 10.
So,
Firstly the numerators 15 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{150}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{15}{10}\) as hundredths in the fraction form is: \(\frac{150}{100}\)
The representation of \(\frac{150}{100}\) in the decimal form is: 1.50
Question 12.
DIG DEEPER!
Complete the table. Think: Can all of the numbers in the table be written as hundredths?
Answer: Yes, all the numbers in the table can be written as hundredths.
Explanation:
A) The given mixed fraction is: 23\(\frac{7}{10}\)
So,
The representation of 23\(\frac{7}{10}\) in the fraction form is: \(\frac{237}{10}\)
So,
To write 23\(\frac{7}{10}\) as hundredths, multiply the fraction and numerator of 23\(\frac{7}{10}\) with 10.
So,
Firstly the numerators 7 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of 23\(\frac{70}{100}\) in the place-value chart is:

Hence,
The representation of 23\(\frac{7}{10}\) as hundredths in the fraction form is: 23\(\frac{70}{100}\)
The representation of 23\(\frac{70}{100}\) in the decimal form is: 23.70
B) The given mixed fraction is: 18\(\frac{2}{10}\)
So,
The representation of 18\(\frac{2}{10}\) in the fraction form is: \(\frac{182}{10}\)
So,
To write 18\(\frac{2}{10}\) as hundredths, multiply the fraction and numerator of 18\(\frac{2}{10}\) with 10.
So,
Firstly the numerators 2 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of 18\(\frac{20}{100}\) in the place-value chart is:
Hence,
The representation of 18\(\frac{2}{10}\) as hundredths in the fraction form is: 18\(\frac{20}{100}\)
The representation of 18\(\frac{20}{100}\) in the decimal form is: 18.20
Hence, in the same way, C) and D) Expressions can also be written as hundredths and in the decimal form
Think and Grow: Modeling Real Life
Example
You use 100 tiles to make a mosaic. 80 of them are square tiles. Your friend uses 10 tiles to make a mosaic. Six of them are square tiles. Do the mosaics have the same fraction of square tiles?


Determine whether the fractions are equivalent.
Write your friend’s fraction as hundredths in fraction form. Then compare.
Hence,
The mosaics don’t have the same fraction of square tiles.
Show and Grow
Question 13.
You use 10 beads to make a bracelet. Seven of them are purple. Your friend uses 100 beads to make a bracelet. 70 of them are purple. Do the bracelets have the same fraction of purple beads?

Answer: Yes, the bracelets have the same fraction of purple beads.
Explanation:
It is given that you use 10 beads to make a bracelet and out of 10 beads, seven of them are purple.
So,
The portion of the bracelet that is purple is: \(\frac{7}{10}\)
So,
The given fraction is: \(\frac{7}{10}\)
So,
To write \(\frac{7}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{7}{10}\) with 10.
So,
Firstly the numerators 7 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{70}{100}\) in the place-value chart is:
Hence,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
It is also given that your friend uses 100 beads to make a bracelet and out of 100, 70 beads are purple.
So,
The portion of purple beads from the total number of beads is: \(\frac{70}{100}\)
Hence, from the above,
We can conclude that the bracelet has the same fraction of purple beads
Question 14.
DIG DEEPER!
The model represents the types of trees on a tree farm. What portion of the tree farm is blue spruce? Fraser fir? white pine? Write your answers as decimals in tenths.
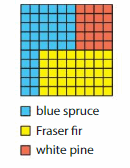
Answer:
The portion of the tree farm that is blue spruce is: 0.4
The portion of the tree farm that is Fraser fir is: 0.4
The portion of the tree farm that is White pine is: 0.2
Explanation:
It is given that the below model represents the types of trees on a tree farm.
The given model is:

In the given model, there are 3 categories of trees
In the given model, each box represents 1 unit.
So,
From the model,
The number of trees of blue spruce is: 40
The number of trees of Frazer fir is: 40
The number of trees of White pine is: 20
The total number of trees in a tree farm is: 100
So,
The portion of the tree farm that is blue spruce from the total number of instruments in the fraction form is: \(\frac{40}{100}\)
The portion of the tree farm that is Frazer fir from the total number of instruments in the fraction form is: \(\frac{40}{100}\)
The portion of the tree farm that is White pine from the total number of instruments in the fraction form is: \(\frac{20}{100}\)
Now, for the Blue spruce,
So,
To write \(\frac{40}{100}\) as tenths, divide the fraction and numerator of \(\frac{40}{100}\) with 10.
So,
Firstly the numerators 40 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{40}{100}=\frac{40 \div 10}{100 \div 10}=\frac{4}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{4}{10}\) in the place-value chart is:

Hence,
The representation of \(\frac{4}{10}\) as tenths in the decimal form is: 0.4
Now, for the Frazer fir,
So,
To write \(\frac{40}{100}\) as tenths, divide the fraction and numerator of \(\frac{40}{100}\) with 10.
So,
Firstly the numerators 40 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{40}{100}=\frac{40 \div 10}{100 \div 10}=\frac{4}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{4}{10}\) in the place-value chart is:

Hence,
The representation of \(\frac{4}{10}\) as tenths in the decimal form is: 0.4
Now, for the White pine,
So,
To write \(\frac{20}{100}\) as tenths, divide the fraction and numerator of \(\frac{20}{100}\) with 10.
So,
Firstly the numerators 20 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{20}{100}=\frac{20 \div 10}{100 \div 10}=\frac{4}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{2}{10}\) in the place-value chart is:
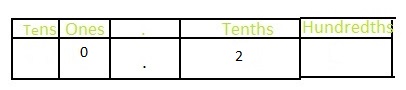
Hence,
The representation of \(\frac{2}{10}\) as tenths in the decimal form is: 0.2
Hence, from the above,
We can conclude that
The portion of the tree farm that is blue spruce is: 0.4
The portion of the tree farm that is Fraser fir is: 0.4
The portion of the tree farm that is White pine is: 0.2
Fractions and Decimals Homework & Practice 10.3
Write the number as tenths in fraction form and decimal form.
Question 1.
\(\frac{40}{100}\)
Answer:
The representation of \(\frac{40}{100}\) as tenths in the fraction form is: \(\frac{4}{10}\)
The representation of \(\frac{4}{10}\) in the decimal form is: 0.4
Explanation:
The given fraction is: \(\frac{40}{100}\)
So, to write \(\frac{40}{100}\) as tenths, divide the fraction and numerator of \(\frac{40}{100}\) with 10.
So,
Firstly the numerators 40 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{40}{100}=\frac{40 \div 10}{100 \div 10}=\frac{5}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{4}{10}\) in the place-value chart is:
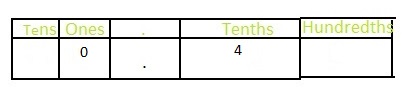
Hence,
The representation of \(\frac{40}{100}\) as tenths in the fraction form is: \(\frac{4}{10}\)
The representation of \(\frac{4}{10}\) in the decimal form is: 0.4
Question 2.
\(\frac{70}{100}\)
Answer:
The representation of \(\frac{70}{100}\) as tenths in the fraction form is: \(\frac{7}{10}\)
The representation of \(\frac{7}{10}\) in the decimal form is: 0.7
Explanation:
The given fraction is: \(\frac{70}{100}\)
So, to write \(\frac{70}{100}\) as tenths, divide the fraction and numerator of \(\frac{70}{100}\) with 10.
So,
Firstly the numerators 70 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{70}{100}=\frac{70 \div 10}{100 \div 10}=\frac{7}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{7}{10}\) in the place-value chart is:

Hence,
The representation of \(\frac{70}{100}\) as tenths in the fraction form is: \(\frac{7}{10}\)
The representation of \(\frac{7}{10}\) in the decimal form is: 0.7
Question 3.
0.20
Answer:
The representation of 2.20 as tenths in the fraction form is: \(\frac{2}{10}\)
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Explanation:
The given decimal number is: 0.20
So,
the representation of 0.20 in the fraction orm is: \(\frac{20}{100}\)
So, to write \(\frac{20}{100}\) as tenths, divide the fraction and numerator of \(\frac{20}{100}\) with 10.
So,
Firstly the numerators 20 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{20}{100}=\frac{20 \div 10}{100 \div 10}=\frac{2}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{2}{10}\) in the place-value chart is:
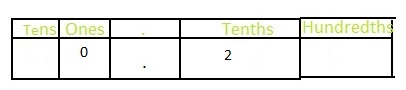
Hence,
The representation of \(\frac{20}{100}\) as tenths in the fraction form is: \(\frac{2}{10}\)
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Write the number as hundredths in fraction form and decimal form
Question 4.
\(\frac{8}{10}\)
Answer:
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
The representation of \(\frac{80}{100}\) in the decimal form is: 0.80
Explanation:
The given fraction is: \(\frac{8}{10}\)
So, to write \(\frac{8}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{8}{10}\) with 10.
So,
Firstly the numerators 8 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{80}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
The representation of \(\frac{80}{100}\) in the decimal form is: 0.80
Question 5.
0.5
Answer:
The representation of 0.5 as hundredths in the fraction form is: \(\frac{50}{100}\)
The representation of \(\frac{50}{100}\) in the decimal form is: 0.50
Explanation:
The given decimal number is: 0.5
So,
The representation of 0.5 in the fraction form is: \(\frac{5}{10}\)
So, to write \(\frac{5}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{5}{10}\) with 10.
So,
Firstly the numerators 5 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{50}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
The representation of \(\frac{50}{100}\) in the decimal form is: 0.50
Question 6.
9\(\frac{6}{10}\)
Answer:
The representation of 9\(\frac{6}{10}\) as hundredths in the fraction form is: 9\(\frac{60}{100}\)
The representation of 9\(\frac{60}{100}\) in the decimal form is: 9.60
Explanation:
The given mixed fraction is: 9\(\frac{6}{10}\)
So,
To write 9\(\frac{6}{10}\) as hundredths, multiply the fraction and numerator of 9\(\frac{6}{10}\) with 10.
So,
Firstly the numerators 6 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of 9\(\frac{60}{100}\) in the place-value chart is:
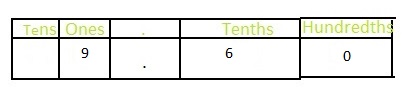
Hence,
The representation of 9\(\frac{6}{10}\) as hundredths in the fraction form is: 9\(\frac{60}{100}\)
The representation of 9\(\frac{60}{100}\) in the decimal form is: 9.60
Write the number represented by the point as hundredths in fraction form and decimal form.

Answer:
From the above number line,
‘A’ value is: 0.3
‘B’ value is: 0.6
‘c’ value is: 1.8
Question 7.
A
Answer:
From the above number line, ‘A’ is: 0.3
The representation of 0.3 as hundredths in the fraction form is: \(\frac{30}{100}\)
The representation of \(\frac{30}{100}\) in the decimal form is: 0.30
Explanation:
The given decimal number is: 0.3
So,
The representation of 0.3 in the fraction form is: \(\frac{3}{10}\)
So,
To write \(\frac{3}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{3}{10}\) with 10.
So,
Firstly the numerators 3 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{30}{100}\) in the place-value chart is:
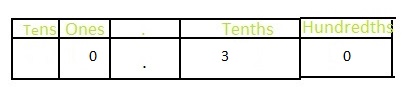
Hence,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
The representation of \(\frac{30}{100}\) in the decimal form is: 0.30
Question 8.
B
Answer:
From the above number line, ‘A’ is: 0.6
The representation of 0.6 as hundredths in the fraction form is: \(\frac{60}{100}\)
The representation of \(\frac{60}{100}\) in the decimal form is: 0.60
Explanation:
The given decimal number is: 0.6
So,
The representation of 0.6 in the fraction form is: \(\frac{6}{10}\)
So,
To write \(\frac{6}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{6}{10}\) with 10.
So,
Firstly the numerators 6 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{60}{100}\) in the place-value chart is:
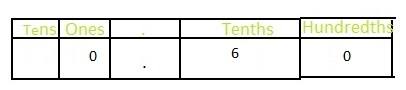
Hence,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
The representation of \(\frac{60}{100}\) in the decimal form is: 0.60
Question 9.
C
Answer:
From the above number line, ‘A’ is: 1.8
The representation of 1.8 as hundredths in the fraction form is: 1\(\frac{80}{100}\)
The representation of 1\(\frac{80}{100}\) in the decimal form is: 1.80
Explanation:
The given decimal number is: 1.8
So,
The representation of 1.8 in the fraction form is: 1\(\frac{8}{10}\)
So,
To write 1\(\frac{8}{10}\) as hundredths, multiply the fraction and numerator of 1\(\frac{8}{10}\) with 10.
So,
Firstly the numerators 8 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of 1\(\frac{80}{100}\) in the place-value chart is:

Hence,
The representation of 1\(\frac{8}{10}\) as hundredths in the fraction form is: 1\(\frac{80}{100}\)
The representation of 1\(\frac{80}{100}\) in the decimal form is: 1.80
Question 10.
Precision
Which of the following show forty-one and nine-tenths?
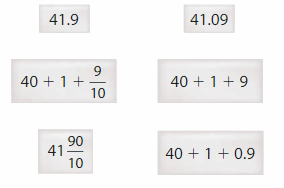
Answer:
Let the given Expressions be named as:
A) 41.9 B) 41.09 C) 40 + 1 + \(\frac{9}{10}\) D) 40 + 1 + 9 E) 41\(\frac{90}{10}\) F) 40 + 1 + 0.9
Hence,
The representation of forty-one and nine-tenths is shown by: B), C) and F)
Explanation:

Let the given Expressions be named as:
A) 41.9 B) 41.09 C) 40 + 1 + \(\frac{9}{10}\) D) 40 + 1 + 9 E) 41\(\frac{90}{10}\) F) 40 + 1 + 0.9
Now,
The given word form is: Forty-one and nine-tenths
The representation of forty-one and nine-tenths in the fraction form is: 41\(\frac{9}{10}\)
So,
The expanded form of 41\(\frac{9}{10}\) is: 40 + 1 + \(\frac{9}{10}\)
The expanded form of 41\(\frac{9}{10}\) in the decimal form is: 40 + 1 + 0.9
The standard form of 41\(\frac{9}{10}\) is: 41.09
Hence, from the above,
We can conclude that Expressions B), C), and F) representing 41\(\frac{9}{10}\)
Question 11.
Which One Doesn’t Belong? Which one does not belong with the other three?
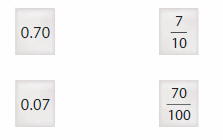
Answer:
Let the Expressions be named as:
A) 0.70 B) \(\frac{7}{10}\) C) 0.07 D) \(\frac{70}{100}\)
Hence, from above,
Expression C) does not belong to the other three.
Explanation:
Let the Expressions be named as:
A) 0.70 B) \(\frac{7}{10}\) C) 0.07 D) \(\frac{70}{100}\)
Now,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
So,
To write \(\frac{7}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{7}{10}\) with 10.
So,
Firstly the numerators 7 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{70}{100}\) in the place-value chart is:
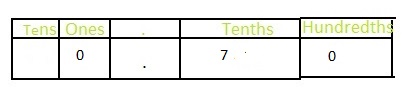
Hence, from the above,
We can conclude that Expression C) does not belong to the other three.
Question 12.
YOU BE THE TEACHER
Is Newton correct? Explain.

Answer: Yes, Newton is correct
Explanation:
The given numbers are: 80 and 0.8
When we compare 80 and 0.8,
We can say that 0.8 is the number that we can obtain when we divide 80 with 100
So,
We can observe that 80 is the whole number and 0.8 is the decimal number
We know that,
The whole number is always greater than the decimal number.
Hence, from the above,
We can conclude that 80 is greater than 0.8 as 80 is greater than 8 according to Newton
Question 13.
Number Sense
Write two equivalent fractions and two equivalent decimals represented by the model.
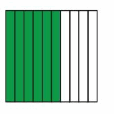
Answer:
The equivalent fractions of \(\frac{6}{10}\) are: \(\frac{60}{100}\) and \(\frac{6}{10}\)
The equivalent decimals represented by \(\frac{6}{10}\) are: 0.6 and 0.60
Explanation:
The given model is:

From the above model,
The total number of parts are: 10
The number of colored parts is: 6
Hence,
The portion of the colored part out of the total number of parts is: \(\frac{6}{10}\)
Now,
The given fraction is: \(\frac{6}{10}\)
So, to write \(\frac{6}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{6}{10}\) with 10.
So,
Firstly the numerators 6 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{60}{100}\) in the place-value chart is:

The representation of \(\frac{6}{10}\) in the place-value chart is:

Hence,
The equivalent fractions of the given model is: \(\frac{60}{100}\) and \(\frac{6}{10}\)
The equivalent decimal numbers of \(\frac{6}{10}\) are: 0.6 and 0.60
Question 14.
Modeling Real Life
Does each player get a base hit on the same fraction of pitches? Explain.

Answer: Yes, each player gets a base hit on the same fraction of pitches.
Explanation:
It is given that there are 2 types of players. They are: Major League player and Youth League player
It is also given that the Major League player gets a base hit on 30 out of 100 pitches and youth League player gets a base hit on 3 out of 10 pitches
So, for comparison, convert the youth League player’s base hit into hundredths.
Now,
The representation of the youth League plyer’s base hit is: \(\frac{3}{10}\)
So,
To write \(\frac{3}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{3}{10}\) with 10.
So,
Firstly the numerators 3 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{30}{100}\) in the place-value chart is:
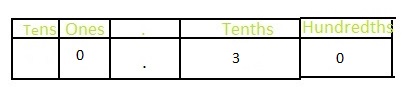
Hence, from the above,
we can conclude that each player gets a base hit on the same fraction of pitches.
Review & Refresh
Find the equivalent fraction
Question 15.
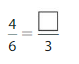
Answer: The equivalent fraction of \(\frac{4}{6}\) is: \(\frac{2}{3}\)
Explanation:
The given fraction is \(\frac{4}{6}\)
From the above fraction, the numerator and denominator are: 4 and 6
4 and 6 are the multiples of 2. ( Since the the numerator and the denominator are the even numbers )
So,
We have to divide the \(\frac{4}{6}\) with 2
So,
\(\frac{4}{6}=\frac{4 \div 2}{6 \div 2}=\frac{2}{3}\)
Hence,
The equivalent fraction of \(\frac{4}{6}\) is: \(\frac{2}{3}\)
Question 16.
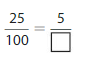
Answer: The equivalent fraction of \(\frac{25}{100}\) is: \(\frac{5}{20}\)
Explanation:
The given fraction is \(\frac{25}{100}\)
From the above fraction, the numerator and denominator are: 25 and 100
25 and 100 are the multiples of 5. ( Since the the numerator and the denominator are the multiples of 5 )
So,
We have to divide the \(\frac{25}{100}\) with 5
So,
\(\frac{25}{100}=\frac{25 \div 5}{100 \div 5}=\frac{5}{20}\)
Hence,
The equivalent fraction of \(\frac{25}{100}\) is: \(\frac{5}{20}\)
Question 17.

Answer: The equivalent fraction of \(\frac{14}{8}\) is: \(\frac{7}{4}\)
Explanation:
The given fraction is \(\frac{14}{8}\)
From the above fraction, the numerator and denominator are: 14 and 8
14 and 8 are the multiples of 2. ( Since the the numerator and the denominator are the even numbers )
So,
We have to divide the \(\frac{14}{8}\) with 2
So,
\(\frac{14}{8}=\frac{14 \div 2}{8 \div 2}=\frac{7}{4}\)
Hence,
The equivalent fraction of \(\frac{14}{8}\) is: \(\frac{7}{4}\)
Lesson 10.4 Compare Decimals
Use models to compare the decimals.
![]()
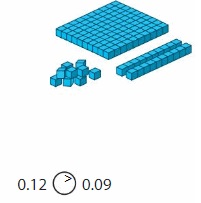
![]()
Answer: 
By using the models, we can compare the number of boxes for the comparison of the decimal numbers.
Each box represents 1 unit out of 100 total units.
So,
The denominator will be the same i.e., the total number of boxes will be the same.
So, we have to compare only numerators i.e., the number of colored boxes so that we can compare the decimal numbers
Reasoning
How did you use your models to determine which decimal is greater?
Answer: For the comparison of the decimals, equate either the numerator or the denominator so that we can compare the numerators.
If we compare the numerators, then we have to make the denominators equal
If we compare the denominators, then we have to make the numerators equal
Hence, in this way, we can compare the decimal numbers.
Think and Grow: Compare Decimals
Example
Compare 0.7 and 0.07.
Answer: 0.7 is greater than 0.07
Explanation:
The given decimal numbers are: 0.7 and 0.07
The representation of 0.7 in the fraction form is: \(\frac{7}{10}\)
The representation of 0.07 in the fraction form is: \(\frac{7}{100}\)
So,
for comparison, we have to make the denominators equal.
So,
Multiply \(\frac{7}{10}\) with 10
So for \(\frac{7}{10}\),
The numerator is 7 and denominator is 10
So,
The numerator 7 is multiplied by 10 and the denominator is also multiplied by 10 to make the denominators equal.
So,
The representation of \(\frac{7}{10}\) in the hundredth’s form is: \(\frac{70}{100}\)
Hence, from the above,
We can conclude that 0.7 is greater than 0.07 by comparing their fraction forms.
Example
Use a place value chart. Start at the left. Compare the digits in each place until the digits differ.
The digits in the one’s place are the same. Compare the tenths.
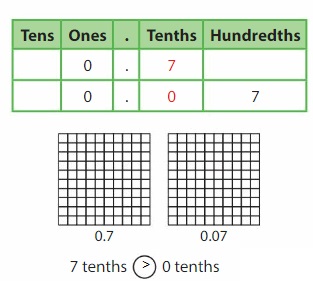
So, 0.7 > 0.07
Example
Compare 0.25 and 0.3.
Use a number line. 0.25 is 25 hundredths. 0.3 and 0.30 are equivalent decimals. So, 0.3 is equivalent to 30 hundredths.
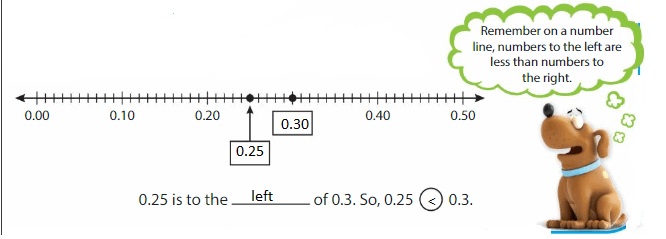
Show and Grow
Compare.
Question 1.
Answer: 0.46 is less than 0.44
Explanation:
The given decimal numbers are: 0.46 and 0.44
The representation of 0.46 and 0.44 in the place-value chart is:
So,
From the above place-value chart,
we can observe that one’s and tenth’s positions are the same.
So,
Compare the hundredth’s position 6 and 4
So, 6 hundredths > 4 hundredths
Hence, from the above,
We can conclude that 0.46 is greater than 0.44
Question 2.
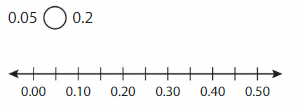
Answer: 0.05 is less than 0.2
Explanation:
The given decimal numbers are 0.05 and 0.2
The representation of 0.05 in the fraction form is: \(\frac{5}{100}\)
The representation of 0.2 in the fraction form is: \(\frac{2}{10}\)
So, for comparison, change \(\frac{2}{10}\) in to hundredths
So, for the change of \(\frac{2}{10}\) in to hundredths, multiply \(\frac{2}{10}\) with 10
So,
The numerator 2 is multiplied by 10 and the denominator 10 is multiplied with 10
Hence,
The representation of 0.2 in hundredth’s form is: \(\frac{20}{100}\)
So, for comparison,
The given number line is:

So, from the above number line,
0.05 is to the left of 0.20
Hence, from the above,
We can conclude that 0.05 is less than 0.20
Apply and Grow: Practice
Use the number line to compare.

Question 3.
![]()
Answer: 0.85 is less than 0.96
Explanation:
The given decimal numbers are: 0.85 and 0.96
The given number line is:

From the above number line, 0.85 is to the left of 0.90
Hence, from the above,
We can conclude that 0.85 is less than 0.90
Question 4.
![]()
Answer: 0.25 is less than 0.52
Explanation:
The given decimal numbers are: 0.25 and 0.52
The given number line is:

From the above number line,
0.25 is to the left of 0.52
Hence, from the above,
We can conclude that 0.25 is less than 0.52
Explanation:
Question 5.
![]()
Answer: 0.11 is greater than 0.09
Explanation:
The given decimal numbers are: 0.11 and 0.09
The given number line is:

From the above line, we can observe that,
0.11 is to the right of 0.09
Hence, from the above,
we can conclude that 0.11 is greater than 0.09
Question 6.
![]()
Answer: 0.72 is greater than 0.59
Explanation:
The given decimal numbers are: 0.72 and 0.59
The given number line is:

From the above number line, we can observe that,
0.72 is to the right of 0.59
Hence, from the above,
We can conclude that 0.72 is greater than 0.59
Question 7.
![]()
Answer: 0.04 is less than 0.40
Explanation:
The given decimal numbers are: 0.04 and 0.40
The given number line is:

From the above number line, we can observe that
0.04 is to the left of 0.40
Hence, from the above,
we can conclude that 0.04 is less than 0.40
Question 8.
![]()
Answer: 0.90 is equal to 0.9
Explanation:
The given decimal numbers are: 0.90 and 0.9
Change the 0.9 into hundredths by multiplying 0.9 with 10.
Now,
The representation of 0.9 in the fraction form is: \(\frac{9}{10}\)
So,
When we multiply \(\frac{9}{10}\) with 10, we can get
The representation of \(\frac{9}{10}\) in hundredth’s in the fraction form is: \(\frac{90}{100}\)
Now,
the given number line is:

We get the numer \(\frac{90}{100}\) by convrting the \(\frac{9}{10}\) and the given number is also \(\frac{90}{100}\)
Hence, from the above,
we can conclude that 0.90 is equal to 0.9
Question 9.
![]()
Answer: 0.3 is greater than 0.03
Explanation:
The given decimal numbers are: 0.3 and 0.03
The representation of 0.3 in the fraction form is: \(\frac{3}{10}\)
The representation of 0.03 in the fraction form is: \(\frac{3}{100}\)
So, for the conversion of \(\frac{3}{10}\) into hundredth’s, we have to multiply \(\frac{3}{10}\) with 10
So,
The representation of \(\frac{3}{10}\) as hundredth’s in the fraction form is: \(\frac{30}{100}\)
The given number line is:

From the above number line, we can observe that
0.03 is to the left of 0.30
Hence, from the above,
We can observe that 0.03 is less than 0.30
Compare
Question 10.
![]()
Answer: 5.29 is greater than 5.24
Explanation:
The given decimal numbers are: 5.29 and 5.24
The representation of 5.29 and 5.24 in the place-value chart is:
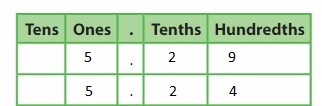
From the above place-value chart, we can observe that one’s and the tenth’s positions are the same.
So,
We have to compare the hundredth’s position of the two decimal numbers.
So, 9 hundredths > 4 hundredths
Hence, from the above,
we can conclude that 5.29 is greater than 5.24
Question 11.
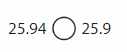
Answer: 25.94 is greater than 25.9
Explanation:
The given decimal numbers are: 25.94 and 25.9
The representation of 25.94 and 25.9 in the place-value chart is:
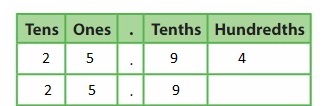
From the above place-value chart, we can observe that ten’s, one’s, and tenth’s positions are the same.
So, we have to compare the hundredth’s position.
So,
4 hundredths > 0 hundredths
Hence, from the above,
we can conclude that 25.94 is greater than 25.9
Open-Ended
Complete the statement to make it true.
Question 12.
![]()
Answer:
Let the missing numbers be 3 and 2
So,
0.31 > 0.21
Explanation:
Let the decimal numbers be: 0.31 and 0.21
The representation of 0.31 and 0.21 in the place-value chart is:
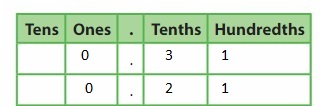
From the above place-value chart,
We can observe that one’s and hundredth’s positions are the same.
So, we have to compare the tenth’s position of the two decimal numbers
So,
3 tenths > 2 tenths
Hence, from the above,
We can conclude that 0.31 is greater than 0.21
Question 13.
![]()
Answer:
Le the missing number be 10
So,
12.10 = 12.10
Explanation:
Let the missing decimal numbers be: 12.10 and 12.10
The representation of 12.10 and 12.10 in the place-value chart is:
From the above place-value chart, we can observe that all the positions are the same.
Hence, from the above,
We can conclude that 12.10 is equal to 12.10
Question 14.
9.43 < ____
Answer:
Let the missing number be: 9.53
So,
9.43 < 9.53
Explanation:
Let the 2 decimal numbers be: 9.43 and 9.53
The representation of 9.43 and 9.53 in the place-value chart is:
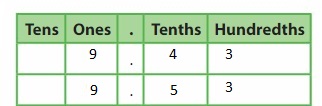
From the above place-value chart, we can observe that one’s position and hundredths position is the same.
So, we can either compare the tenths position.
So,
When we compare the tenths position, 4 tenths < 5 tenths
Hence, from the above
We can conclude that 9.43 is less than 9.53
Question 15.
Precision
Write the number that is halfway between 3.6 and 3.7. Explain how you found your answer.
Answer: The number that is halfway between 3.6 and 3.7 is 3.65
Explanation:
The given decimal numbers are: 3.6 and 3.7
We know that,
The middle number between two numbers = (The given first number + The given second number) ÷ 2
So,
The number that is halfway between 3.6 and 3.7 = (3.6 + 3.7) ÷ 2
= 7.3 ÷ 2
= 3.65
Hence, from the above,
we can conclude that the number that is halfway between 3.6 and 3.7 is: 3.65
DIG DEEPER!
Write whether the statement is true or false. If false, explain why
Question 16.

Answer: \(\frac{1}{10}\) is greater than 0.07
Explanation:
The given numbers are: \(\frac{1}{10}\) and 0.07
The representation of 0.07 in the fraction form is: \(\frac{7}{100}\)
So, for comparison, we have to convert \(\frac{1}{10}\) into hundredths form by multiplying \(\frac{1}{10}\) with 10.
So,
The representation of \(\frac{1}{10}\) as hundredths in the fraction form is: \(\frac{10}{100}\)
The representation of 0.07 in the fraction form is: \(\frac{7}{100}\)
Hence, from the above,
we can conclude that \(\frac{1}{10}\) is greater than 0.07
Question 17.
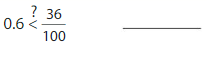
Answer: 0.6 is greater than 0.36
Explanation:
The given numbers are: 0.6 and \(\frac{36}{100}\)
The representation of 0.6 in the fraction form is: \(\frac{6}{10}\)
So, for comparison, we have to convert \(\frac{6}{10}\) into hundredths form by multiplying \(\frac{6}{10}\) with 10.
So,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
The representation of 0.36 in the fraction form is: \(\frac{36}{100}\)
Hence, from the above,
we can conclude that 0.6 is greater than \(\frac{36}{100}\)
Think and Grow: Modeling Real Life
Example
Newton and Descartes make paper airplanes. Newton’s paper Whose airplane flies 3.01 meters. Descartes’s paper airplane flies 3.10 meters. Whose paper airplane flies farther?

Use a place value chart. Compare the digits in each place until the digits differ.
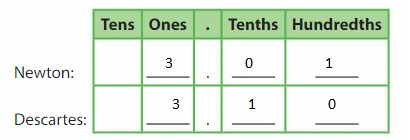
Compare Newton’s distance to Descartes’s distance.
So,
Descartes’s paper airplane flies farther.
Show and Grow
Question 18.
Compare the thickness of a nickel and a quarter. Which coin is thinner?
Answer: When we compare the thickness of nickel and quarter by observing the table, we can say that the Quarter is thinner.
Explanation:
The given table is:

From the given table,
The thickness of the Nickel is: 1.95mm
The thickness of the Quarter is: 1.75mm
Now,
The representation of the thicknesses of the Nickel and the Quarter in the place-value chart is:
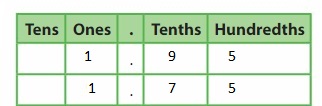
From the above place-value chart, we can observe that
7 tenths < 9 tenths
Hence, from the above,
We can conclude that the Quarter is thinner.
Question 19.
You, your cousin, and your friend run a 100-meter race. Who finishes first? second? third?

Answer:
The one who finishes first is: You
The one who finishes second is: Friend
The one who finishes third is: Cousin
Explanation:
The given timings are:
The timing of yours is: 16.40 seconds
The timing of your friend is: 16.48 seconds
The timing of your cousin is: 16.58 seconds
Now, the representation of all the timings in the place-value chart is:
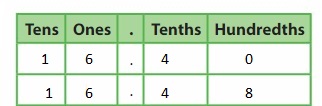
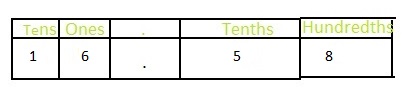
Hence, from the above,
We can conclude that:
The one who finishes first is: You
The one who finishes second is: Friend
The one who finishes third is: Cousin
Question 20.
DIG DEEPER!
Your water bottle is 0.25 full. Your friend’s water bottle is 0.5 full. You have more water than your friend. Explain how this is possible.
Answer: This is not possible.
Explanation:
It is given that your water bottle is 0.25 full and your friend’s water bottle is 0.5 full.
So, we have to compare 0.25 and 0.5
The representation of 0.5 in the fraction form is: \(\frac{5}{10}\)
The representation of 0.25 in the fraction form is: \(\frac{25}{100}\)
So, for comparison, we have to convert \(\frac{5}{10}\) as hundredths by multiplying \(\frac{5}{10} \) with 10.
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
Hence, from the above,
we can conclude that your friend’s water bottle has more water than you.
Compare Decimals Homework & Practice 10.4
Compare
Question 1.
Answer: 0.58 is greater than 0.52
Explanation:
The given decimal numbers are: 0.58 and 0.52
The representation of 0.58 and 0.52 in the place-value chart is:
From the above table, we can observe that one’s and tenth’s positions are the same.
So, we have to compare the hundredth’s position
So,
8 hundredths > 2 hundredths
Hence, from the above,
we can conclude that 0.58 is greater than 0.52
Question 2.
Answer: 0.25 is greater than 0.05
Explanation:
The given decimal numbers are: 0.25 and 0.05
The given number line is:
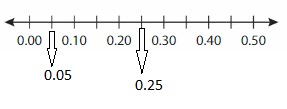
From the above number line,
We can observe that 0.05 is to the left of 0.25
hence, from the above,
We can conclude that 0.25 is greater than 0.05
Use the number line to compare.
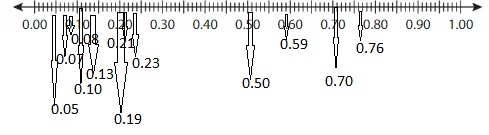
Question 3.
![]()
Answer: 0.76 is greater than 0.59
Explanation:
The given decimal numbers are: 0.76 and 0.59
The given number line is:

From the above number line,
We can observe that 0.76 is to the right of 0.59
Hence, from the above,
we can conclude that 0.76 is greater than 0.59
Question 4.
![]()
Answer: 0.21 is less than 0.23
Explanation:
the given decimal numbers are: 0.21 and 0.23
The given number line is:

From the above number line,
We can observe that 0.21 is to the left of 0.23
Hence, from the above,
we can conclude that 0.21 is less than 0.23
Question 5.
![]()
Answer: 0.7 is greater than 0.07
Explanation:
The given decimal numbers are: 0.7 and 0.07
The representation of 0.7 in the fracton form is: \(\frac{7}{10}\)
So,
The \(\frac{7}{10}\) should be converted into hundredths by multiplying \(\frac{7}{10}\) with 10.
So,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
Now,
The given number line is:

From the above number line,
We can observe that 0.7 is to the left of 0.07
Hence, from the above,
We can conclude that 0.7 is greater than 0.07
Question 6.
![]()
Answer: 0.05 is less than 0.08
Explanation:
The given decimal numbers are: 0.05 and 0.08
The given number line is:

From the above number line,
We can observe that 0.05 is to the left of 0.08
Hence, from the above,
We can conclude that 0.05 is less than 0.08
Question 7.
![]()
Answer: 0.10 is equal to 0.1
Explanation:
The given decimal numbers are: 0.10 and 0.1
Now,
The representation of 0.1 in the fraction form is: \(\frac{1}{10}\)
The representation of 0.10 in the fraction form is: \(\frac{1}{100}\)
Now, to make the denominators equal, multiply \(\frac{1}{10}\) by 2.
So,
The representation of \(\frac{1}{10}\) as hundredths, in the fraction form is: \(\frac{1}{100}\)
Now,
The given number line is:

Hence, from the above,
We can conclude that 0.10 is equal to 0.1
Question 8.
![]()
Answer: 0.05 is less than 0.50
Explanation:
The given decimal numbers are: 0.05 and 0.50
The given number line is:

From the above number line,
We can observe that 0.05 is to the left of 0.50.
Hence, from the above,
we can conclude that 0.05 is less than 0.50
Question 9.
![]()
Answer: 0.13 is less than 0.19
Explanation:
The given decimal numbers are: 0.13 and 0.19
The given number line is:

From the above number line,
We can observe that 0.13 is to the left of 0.10
Hence, from the above,
We can conclude that 0.13 is less than 0.19
Compare
Question 10.
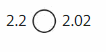
Answer: 2.2 is greater than 2.02
Explanation:
The given decimal numbers are: 2.2 and 2.02
The representation of 2.2 and 2.02 in the place-value chart is:
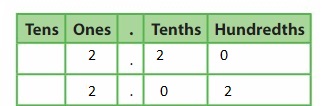
From the above place-value chart,
We can observe that only one’s position is the same
So,
2 tenths > 0 tenths
Hence, from the above,
We can conclude that 2.2 is greater than 2.02
Question 11.
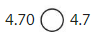
Answer: 4.70 is equal to 4.7
Explanation:
The given decimal numbers are: 4.70 and 4.7
The representation of 4.70 in the fraction form is: 4\(\frac{70}{100}\)
The representation of 4.7 in the fraction form is: 4\(\frac{7}{10}\)
So, to compare, we have to make the denominators equal.
So, multiply 4\(\frac{7}{10}\) with 10
So,
The representation of 4\(\frac{7}{10}\) as hundredth’s in the fraction form is: 4\(\frac{70}{100}\)
Hence, from the above,
We can conclude that 4.70 is equal to 4.7
Question 12.
![]()
Answer: 8.35 is less than 8.53
Explanation:
The given decimal numbers are: 8.35 and 8.53
The representation of 8.35 and 8.53 in the place-value chart is:
From the above place-value chart,
We can observe that only the tenth’s position can be compared.
So,
3 tenths < 5 tenths
Hence, from the above,
We can conclude that 8.35 is less than 8.53
Question 13.
![]()
Answer: 35.01 is greater than 32.98
Explanation:
The given decimal numbers are: 35.01 and 32.98
The representation of 35.01 and 32.98 in the place-value chart is:
From the above place-value chart,
We can compare one’s position since it is the position with the highest value after the ten’s position.
So,
5 ones > 2 ones
Hence, from the above,
we can conclude that 35.01 is greater than 32.98
Question 14.
![]()
Answer: 14.9 is less than 14.92
Explanation:
The given decimal numbers are: 14.9 and 14.92
The representation of 14.9 and 14.92 in the place-value chart is:
From the above place-value chart,
We can compare only the hundredth’s positions.
So,
0 hundredths< 2 hundredths
Hence, from the above,
We can conclude that 14.9 is less than 14.92
Question 15.
Precision
Explain how to compare 0.46 and 0.48.
Answer: 0.46 is less than 0.48
Explanation:
The given decimal numbers are: 0.46 and 0.48
The representation of 0.46 and 0.48 in the place-value chart is:
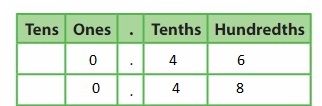
From the above place-value chart,
We can compare the hundredth’s position
So,
6 hundredths < 8 hundredths
Hence, from the above
We can conclude that 0.46 is less than 0.48
Question 16.
Open-Ended
What might Descartes’s number be?

Answer: Descartes’s number might be: 0.61, 0.62, 0.63, 0.64, 0.65
Explanation:
Given that my number is greater than 0.6 and less than 0.7.
So,
The numbers might be: 0.61, 0.62, 0.63, 0.64, 0.65, 0.66, 0.67, 0.68, 0.69
It is also given that the greatest digit in the number is in the tenths place.
So,
The numbers might be: 0.61, 0.62, 0.63, 0.64, 0.65
Hence, from the above,
We can conclude that Descartes’s number might be: 0.61, 0.62, 0.63, 0.64, 0.65
Question 17.
Modeling Real Life
A traffic light is red for 23.4 seconds and green for 23.6 seconds. Does the traffic light stay red or green longer?
Answer: The traffic light stay green for a long time
Explanation:
It is given that a traffic light is red for 23.4 seconds and green for 23.6 seconds.
So, we have to compare 23.4 and 23.6 to see which light stay for a long time
Now,
The representation of 23.4 and 23.6 in the place-value chart is:
From the above place-value chart, we can observe that we can compare only the tenths position.
So,
4 tenths < 6 tenths
So,
23.4 is less than 23.6
Hence, from the above,
We can conclude that the green light stays for a long time
Question 18.
Modeling Real Life
Order the caterpillars from longest to shortest.
Answer: Caterpillar B > Caterpillar A > Caterpillar C
Explanation:
The given table is:

From the table,
The length of caterpillar A is: 3.5 cm
The length of caterpillar B is: 3.65 cm
The length of caterpillar C is: 3.45 cm
So,
When we compare the tenth’s position in all the lengths of the caterpillars,
We can observe that B > A > C
Hence, from the above,
We can conclude that caterpillar B > caterpillar A > caterpillar C
Review & Refresh
Round the number to the nearest hundred thousand
Question 19.
695,023
Answer: The nearest hundred thousand of 695,023 is: 700,000
Explanation:
The given number is: 695,023
We know that,
The value of a digit depends on the position of the digit
So,
The value of the nearest hundred thousand in 695,023 is: 700,000
Question 20.
246,947
Answer: The value of the nearest hundred thousand in 246,947 is: 200,000
Explanation:
The given number is: 246,947
We know that,
The value of a digit depends on the position of the digit
So,
The value of the nearest hundred thousand in 246,947 is: 200,000
Lesson 10.5 Add Decimal Fractions and Decimals
Explore and Grow
How can you use a number line to find the sum?
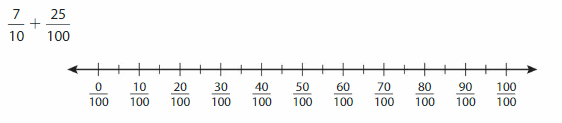
0.25 + 0.7

How can you use models to check your answers?
Answer:
The representation of the sum in the fraction form is:
\(\frac{7}{10}\) + \(\frac{25}{100}\) = \(\frac{95}{100}\)
The representation of the sum in the decimal form is:
0.25 + 0.7 = 0.95
Explanation:
The given fractions are: \(\frac{25}{100}\) and \(\frac{7}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{7}{10}\) as the hundredths, we have to multiply \(\frac{7}{10}\) by 10
So,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
So,
\(\frac{70}{100}\) + \(\frac{25}{100}\)
= \(\frac{70 + 25}{100}\)
= \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal form is: 0.95
Now,

Hence, from the above,
We can conclude that
\(\frac{70}{100}\) + \(\frac{25}{100}\) = \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal form is: 0.95
Reasoning
How can you add two decimal fractions with a denominator of 10? How can you add two decimal fractions with denominators of 10 and 100?
Answer: We add the two fractions only if their numerator or denominators are equal
If there are fractions with different denominators, then we will make the denominators equal either by multiplying or by dividing the fractions and add the different fractions.
Think and Grow: Add Decimal Fractions and Decimals
You have learned how to add fractions with the same denominator. You can use equivalent fractions to add fractions that do not have the same denominator.

Step 1: Use equivalent fractions to write the fractions with the same denominator
Think: Rewrite \(\frac{3}{10}\) with a denominator of 100.
![]()

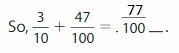
Example
Find 0.75 + 0.2.
Step 1: Write 0.75 and 0.2 as fractions.Think: 0.75 is 75 hundredths. 0.2 is 2 tenths.
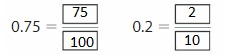
Step 2: Use equivalent fractions to write the fractions with the same denominator.
![]()
Step 3: Add the numerators.
![]()
Step 4: Write the sum as a decimal.
![]()
So, 0.75 + 0.2 = 0.95
Show and Grow
Find the sum.
Question 1.
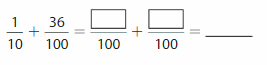
Answer:
The representation of the sum in the fraction form is:
\(\frac{1}{10}\) + \(\frac{36}{100}\) = \(\frac{46}{100}\)
The representation of \(\frac{46}{100}\) in the decimal for is: 0.46
Explanation:
The given fractions are: \(\frac{36}{100}\) and \(\frac{1}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{1}{10}\) as the hundredths, we have to multiply \(\frac{1}{10}\) by 10
So,
The representation of \(\frac{1}{10}\) as hundredths in the fraction form is: \(\frac{10}{100}\)
So,
\(\frac{10}{100}\) + \(\frac{36}{100}\)
= \(\frac{10 + 36}{100}\)
= \(\frac{46}{100}\)
The representation of \(\frac{46}{100}\) in the decimal form is: 0.46
Hence from the above,
We can conclude that
\(\frac{1}{10}\) + \(\frac{36}{100}\) = \(\frac{46}{100}\)
The representation of \(\frac{46}{100}\) in the decimal for is: 0.46
Question 2.
0.5 + 0.25 = ____
Answer:
The representation of the sum in the fraction form is:
\(\frac{5}{10}\) + \(\frac{25}{100}\) = \(\frac{75}{100}\)
The representation of 0.25 + 0.5 in the decimal form is: 0.75
Explanation:
The given decimal numbers are: 0.5 and 0.25
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{25}{100}\) and \(\frac{5}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{5}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) by 10
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{50}{100}\) + \(\frac{25}{100}\)
= \(\frac{50 + 25}{100}\)
= \(\frac{75}{100}\)
The representation of \(\frac{75}{100}\) in the decimal form is: 0.75
Hence from the above,
We can conclude that
\(\frac{5}{10}\) + \(\frac{25}{100}\) = \(\frac{75}{100}\)
The representation of \(\frac{75}{100}\) in the decimal for is: 0.75
Apply and Grow: Practice
Find the sum.
Question 3.
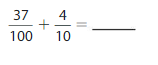
Answer:
The representation of the sum in the fraction form is:
\(\frac{4}{10}\) + \(\frac{37}{100}\) = \(\frac{77}{100}\)
The representation of \(\frac{77}{100}\) in the decimal for is: 0.77
Explanation:
The given fractions are: \(\frac{37}{100}\) and \(\frac{4}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{4}{10}\) as the hundredths, we have to multiply \(\frac{4}{10}\) by 10
So,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
So,
\(\frac{40}{100}\) + \(\frac{37}{100}\)
= \(\frac{40 + 37}{100}\)
= \(\frac{77}{100}\)
The representation of \(\frac{77}{100}\) in the decimal form is: 0.77
Hence from the above,
We can conclude that
\(\frac{4}{10}\) + \(\frac{37}{100}\) = \(\frac{77}{100}\)
The representation of \(\frac{77}{100}\) in the decimal for is: 0.77
Question 4.
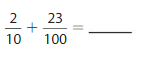
Answer:
The representation of the sum in the fraction form is:
\(\frac{2}{10}\) + \(\frac{23}{100}\) = \(\frac{43}{100}\)
The representation of \(\frac{43}{100}\) in the decimal for is: 0.43
Explanation:
The given fractions are: \(\frac{23}{100}\) and \(\frac{2}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{2}{10}\) as the hundredths, we have to multiply \(\frac{2}{10}\) by 10
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
So,
\(\frac{20}{100}\) + \(\frac{23}{100}\)
= \(\frac{20 + 23}{100}\)
= \(\frac{43}{100}\)
The representation of \(\frac{43}{100}\) in the decimal form is: 0.43
Hence from the above,
We can conclude that
\(\frac{2}{10}\) + \(\frac{23}{100}\) = \(\frac{43}{100}\)
The representation of \(\frac{43}{100}\) in the decimal for is: 0.43
Question 5.
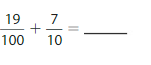
Answer:
The representation of the sum in the fraction form is:
\(\frac{7}{10}\) + \(\frac{19}{100}\) = \(\frac{89}{100}\)
The representation of \(\frac{89}{100}\) in the decimal for is: 0.89
Explanation:
The given fractions are: \(\frac{19}{100}\) and \(\frac{7}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{7}{10}\) as the hundredths, we have to multiply \(\frac{7}{10}\) by 10
So,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
So,
\(\frac{70}{100}\) + \(\frac{19}{100}\)
= \(\frac{70 + 19}{100}\)
= \(\frac{89}{100}\)
The representation of \(\frac{89}{100}\) in the decimal form is: 0.89
Hence from the above,
We can conclude that
\(\frac{7}{10}\) + \(\frac{19}{100}\) = \(\frac{89}{100}\)
The representation of \(\frac{89}{100}\) in the decimal for is: 0.89
Question 6.
0.35 + 0.1 = ____
Answer:
The representation of the sum in the fraction form is:
\(\frac{1}{10}\) + \(\frac{35}{100}\) = \(\frac{45}{100}\)
The representation of 0.35 + 0.1 in the decimal for is: 0.45
Explanation:
The given decimal numbers are: 0.1 and 0.35
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{35}{100}\) and \(\frac{1}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{1}{10}\) as the hundredths, we have to multiply \(\frac{1}{10}\) by 10
So,
The representation of \(\frac{1}{10}\) as hundredths in the fraction form is: \(\frac{10}{100}\)
So,
\(\frac{10}{100}\) + \(\frac{35}{100}\)
= \(\frac{10 + 35}{100}\)
= \(\frac{45}{100}\)
The representation of \(\frac{45}{100}\) in the decimal form is: 0.45
Hence from the above,
We can conclude that
\(\frac{1}{10}\) + \(\frac{35}{100}\) = \(\frac{45}{100}\)
The representation of \(\frac{45}{100}\) in the decimal for is: 0.45
Question 7.
0.8 + 0.15 = ____
Answer:
The representation of the sum in the fraction form is:
\(\frac{8}{10}\) + \(\frac{15}{100}\) = \(\frac{95}{100}\)
The representation of 0.15 + 0.8 in the decimal for is: 0.95
Explanation:
The given decimal numbers are: 0.8 and 0.15
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{15}{100}\) and \(\frac{8}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{8}{10}\) as the hundredths, we have to multiply \(\frac{8}{10}\) by 10
So,
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
So,
\(\frac{80}{100}\) + \(\frac{15}{100}\)
= \(\frac{80 + 15}{100}\)
= \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal form is: 0.95
Hence from the above,
We can conclude that
\(\frac{8}{10}\) + \(\frac{15}{100}\) = \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal for is: 0.95
Question 8.
0.50 + 0.4 = __
Answer:
The representation of the sum in the fraction form is:
\(\frac{4}{10}\) + \(\frac{50}{100}\) = \(\frac{90}{100}\)
The representation of 0.50 + 0.4 in the decimal for is: 0.90
Explanation:
The given decimal numbers are: 0.4 and 0.50
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{50}{100}\) and \(\frac{4}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{4}{10}\) as the hundredths, we have to multiply \(\frac{4}{10}\) by 10
So,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
So,
\(\frac{40}{100}\) + \(\frac{50}{100}\)
= \(\frac{50 + 40}{100}\)
= \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal form is: 0.90
Hence from the above,
We can conclude that
\(\frac{4}{10}\) + \(\frac{50}{100}\) = \(\frac{90}{100}\)
The representation of \(\frac{90}{100}\) in the decimal for is: 0.90
Question 9.
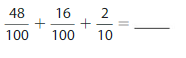
Answer:
The representation of the sum in the fraction form is:
\(\frac{48}{100}\) + \(\frac{16}{100}\) + \(\frac{2}{10}\) = \(\frac{84}{100}\)
The representation of \(\frac{84}{100}\) in the decimal for is: 0.84
Explanation:
The given fractions are: \(\frac{48}{100}\), \(\frac{16}{100}\) and \(\frac{2}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{2}{10}\) as the hundredths, we have to multiply \(\frac{2}{10}\) by 10
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
So,
\(\frac{48}{100}\) + \(\frac{16}{100}\) + \(\frac{20}{100}\)
= \(\frac{48 + 16 + 20}{100}\)
= \(\frac{84}{100}\)
The representation of \(\frac{84}{100}\) in the decimal form is: 0.84
Hence from the above,
We can conclude that
\(\frac{2}{10}\) + \(\frac{48}{100}\) + \(\frac{16}{100}\) = \(\frac{84}{100}\)
The representation of \(\frac{84}{100}\) in the decimal for is: 0.84
Question 10.
0.3 + 0.25 + 0.1 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{3}{10}\) + \(\frac{1}{10}\) + \(\frac{25}{100}\) = \(\frac{65}{100}\)
The representation of 0.25 + 0.1 + 0.3 in the decimal for is: 0.65
Explanation:
The given decimal numbers are: 0.3, 0.1 and 0.25
So, convert the three decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{25}{100}\) , \(\frac{3}{10}\) and \(\frac{1}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{1}{10}\) and \(\frac{3}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) and \(\frac{3}{10}\) by 10
So,
The representation of \(\frac{1}{10}\) as hundredths in the fraction form is: \(\frac{10}{100}\)
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
So,
\(\frac{10}{100}\) + \(\frac{25}{100}\) + \(\frac{30}{100}\)
= \(\frac{10 + 25 + 30}{100}\)
= \(\frac{65}{100}\)
The representation of \(\frac{65}{100}\) in the decimal form is: 0.65
Hence from the above,
We can conclude that
\(\frac{1}{10}\) + \(\frac{25}{100}\) + \(\frac{3}{10}\) = \(\frac{65}{100}\)
The representation of \(\frac{65}{100}\) in the decimal for is: 0.65
Number Sense
Find the sum.
Question 11.
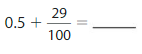
Answer:
The representation of the sum in the fraction form is:
\(\frac{5}{10}\) + \(\frac{29}{100}\) = \(\frac{79}{100}\)
The representation of 0.5 + \(\frac{29}{100}\) in the decimal for is: 0.79
Explanation:
The given numbers are: 0.5 and \(\frac{29}{100}\)
So, convert the decimal number in to respective fractions.
So,
The given fractions are: \(\frac{5}{10}\) and \(\frac{29}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{5}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) by 10
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{50}{100}\) + \(\frac{29}{100}\)
= \(\frac{50 + 29}{100}\)
= \(\frac{79}{100}\)
The representation of \(\frac{79}{100}\) in the decimal form is: 0.79
Hence from the above,
We can conclude that
\(\frac{5}{10}\) + \(\frac{29}{100}\) = \(\frac{79}{100}\)
The representation of \(\frac{79}{100}\) in the decimal for is: 0.79
Question 12.
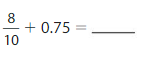
Answer:
The representation of the sum in the fraction form is:
\(\frac{8}{10}\) + \(\frac{75}{100}\) = \(\frac{155}{100}\)
The representation of 0.75 + \(\frac{8}{10}\) in the decimal for is: 1.55
Explanation:
The given numbers are: 0.75 and \(\frac{8}{10}\)
So, convert the decimal number in to respective fractions.
So,
The given fractions are: \(\frac{8}{10}\) and \(\frac{75}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{8}{10}\) as the hundredths, we have to multiply \(\frac{8}{10}\) by 10
So,
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
So,
\(\frac{80}{100}\) + \(\frac{75}{100}\)
= \(\frac{80 + 75}{100}\)
= \(\frac{155}{100}\)
The representation of \(\frac{155}{100}\) in the decimal form is: 1.55
Hence from the above,
We can conclude that
\(\frac{8}{10}\) + \(\frac{75}{100}\) = \(\frac{155}{100}\)
The representation of \(\frac{155}{100}\) in the decimal for is: 1.55
Question 13.
YOU BE THE TEACHER
Your friend says Newton and Descartes are both correct. Is your friend correct? Explain.

Answer: Yes, your friend is correct.
Explanation:
The representation of the sum in the fraction form is:
\(\frac{5}{10}\) + \(\frac{5}{100}\) + \(\frac{55}{100}\) = \(\frac{110}{100}\)
The representation of 0.55 + 0.5 + 0.05 in the decimal for is: 1.10
Explanation:
The given decimal numbers are: 0.05, 0.5 and 0.55
So, convert the three decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{55}{100}\) , \(\frac{5}{10}\) and \(\frac{5}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{5}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) by 10
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{50}{100}\) + \(\frac{55}{100}\) + \(\frac{5}{100}\)
= \(\frac{50 + 55 + 5}{100}\)
= \(\frac{110}{100}\)
The representation of \(\frac{110}{100}\) in the decimal form is: 1.10
Hence from the above,
We can conclude that
\(\frac{5}{10}\) + \(\frac{55}{100}\) + \(\frac{5}{100}\) = \(\frac{110}{100}\)
The representation of \(\frac{110}{100}\) in the decimal for is: 1.10 or 1.1
Question 14.
DIG DEEPER!
Write and solve a decimal addition problem represented by the model. Write your answer as a decimal and as a mixed number.
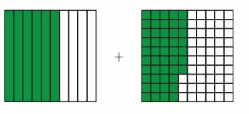
Answer:
From the above model,
The representation of the sum in the fraction form is:
\(\frac{6}{10}\) + \(\frac{47}{100}\) = \(\frac{107}{100}\) = 1\(\frac{7}{100}\)
The representation of \(\frac{107}{100}\) in the decimal for is: 1.07
Explanation:
The given model is:

From the model,
The given fractions are: \(\frac{47}{100}\) and \(\frac{6}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{6}{10}\) as the hundredths, we have to multiply \(\frac{6}{10}\) by 10
So,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
So,
\(\frac{60}{100}\) + \(\frac{47}{100}\)
= \(\frac{60 + 47}{100}\)
= \(\frac{107}{100}\)
The representation of \(\frac{107}{100}\) in the decimal form is: 1.07
Hence from the above,
We can conclude that
\(\frac{6}{10}\) + \(\frac{47}{100}\) = \(\frac{107}{100}\) = 1\(\frac{7}{100}\)
The representation of \(\frac{107}{100}\) in the decimal for is: 1.07
Think and Grow: Modeling Real Life
Example
You use \(\frac{8}{10}\) pound of clay to make a cup. You make a handle for the cup with \(\frac{15}{100}\) pound of clay and attach the handle to the cup. What fraction of a pound does your cup weigh in all?
Add the fractions.

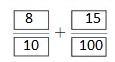
Use equivalent fractions to write the fractions with the same denominator.
Rewrite \(\frac{8}{10}\) with a denominator of 100.
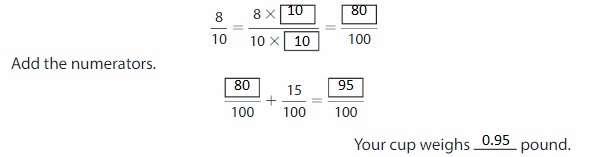
Show and Grow
Question 15.
Each morning, you walk \(\frac{25}{100}\) mile to your friend’s house and then \(\frac{5}{10}\) mile to school. What fraction of a mile do you walk each morning?
Answer:
The fraction of a mile you walk each morning is:
\(\frac{25}{100}\) + \(\frac{5}{10}\) = \(\frac{75}{100}\)
Explanation:
It is given that each morning, you walk \(\frac{25}{100}\) mile to your friend’s house and then \(\frac{5}{10}\) mile to school.
So,
To find the portion of a mile you walk in the morning, you have to add the fractions.
So,
Now, first, we have to convert \(\frac{5}{10}\) as hundredths so that we can add both the fractions because denominators have to be equal for the addition.
So,
Multiply \(\frac{5}{10}\) with 10 to convert it as hundredths
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{25}{100}\) + \(\frac{50}{100}\)
= \(\frac{75}{100}\)
Hence, from the above,
We can conclude that the portion of a mile you walk in the morning is: \(\frac{75}{100}\)
Question 16.
You ride a zip line that is mile-long \(\frac{15}{100}\) mile long. You ride another zip line that is \(\frac{3}{10}\) mile long. Your friend rides a total of \(\frac{40}{100}\) mile on zip lines. Who rides farther on zip lines?

Answer: Your friend rides farther on zip lines.
Explanation:
It is given that you ride a zip line that is mile-long \(\frac{15}{100}\) mile long. You ride another zip line that is \(\frac{3}{10}\) mile long and your friend rides a total of \(\frac{40}{100}\) mile on zip
lines.
So, the given three fractions are:
\(\frac{15}{100}\), \(\frac{3}{10}\) and \(\frac{40}{100}\)
So, for the comparison of the three fractions, we have to make the denominators equal.
So, we have to convert \(\frac{3}{10}\) as hundredths.
So,
We have to multiply \(\frac{3}{10}\) with 10
So,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
Now,
As the denominators are equal, compare the numerators.
So, we have to compare 15, 30, and 40
By comparing, we can observe that 40 > 30 > 15
Hence, from the above,
We can conclude that your friend rides farther on zip lines than you.
Question 17.
DIG DEEPER!
You ship a package that weighs 0.8 pounds. Your package is 0.75 pounds lighter than your friend’s package. How much does your friend’s package weigh? Write your answer in decimal form.
Answer: The weight of your friend’s package is: 1.55 pounds
Explanation:
The two given decimal numbers are: 0.8 and 0.75
It is given that your package is 0.75 pounds lighter than your friend’s package.
So,
The weight of your friend’s package = 0.8 + 0.75
Now, first, convert the given decimal numbers into fractions.
So, The representation of 0.8 and 0.75 in the fraction forms is: \(\frac{8}{10}\) and \(\frac{75}{100}\)
Now, for addition, we have to make the denominators of the two fractions equal.
So,
We have to multiply \(\frac{3}{10}\) with 10, to make the denominator equal to 100
So,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
So,
\(\frac{30}{100}\) + \(\frac{75}{100}\)
= \(\frac{105}{100}\)
The representation of \(\frac{105}{100}\) in the decimal form is: 1.05
Hence, from the above,
We can conclude that the weight of your friend’s package in the decimal form is: 1.05 pounds
Add Decimal Fractions and Decimals Homework & Practice 10.5
Find the sum.
Question 1.
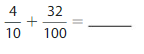
Answer:
The representation of the sum in the fraction form is:
\(\frac{4}{10}\) + \(\frac{32}{100}\) = \(\frac{72}{100}\)
The representation of \(\frac{72}{100}\) in the decimal for is: 0.72
Explanation:
The given fractions are: \(\frac{32}{100}\) and \(\frac{4}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{4}{10}\) as the hundredths, we have to multiply \(\frac{4}{10}\) by 10
So,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
So,
\(\frac{40}{100}\) + \(\frac{32}{100}\)
= \(\frac{40 + 32}{100}\)
= \(\frac{72}{100}\)
The representation of \(\frac{72}{100}\) in the decimal form is: 0.72
Hence from the above,
We can conclude that
\(\frac{4}{10}\) + \(\frac{32}{100}\) = \(\frac{72}{100}\)
The representation of \(\frac{72}{100}\) in the decimal for is: 0.72
Question 2.
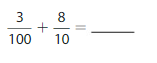
Answer:
The representation of the sum in the fraction form is:
\(\frac{8}{10}\) + \(\frac{3}{100}\) = \(\frac{83}{100}\)
The representation of \(\frac{83}{100}\) in the decimal for is: 0.83
Explanation:
The given fractions are: \(\frac{3}{100}\) and \(\frac{8}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{8}{10}\) as the hundredths, we have to multiply \(\frac{8}{10}\) by 10
So,
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
So,
\(\frac{80}{100}\) + \(\frac{3}{100}\)
= \(\frac{80 + 3}{100}\)
= \(\frac{83}{100}\)
The representation of \(\frac{83}{100}\) in the decimal form is: 0.83
Hence from the above,
We can conclude that
\(\frac{8}{10}\) + \(\frac{3}{100}\) = \(\frac{83}{100}\)
The representation of \(\frac{83}{100}\) in the decimal for is: 0.83
Question 3.
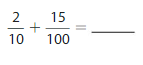
Answer:
The representation of the sum in the fraction form is:
\(\frac{2}{10}\) + \(\frac{15}{100}\) = \(\frac{35}{100}\)
The representation of \(\frac{35}{100}\) in the decimal for is: 0.35
Explanation:
The given fractions are: \(\frac{15}{100}\) and \(\frac{2}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{2}{10}\) as the hundredths, we have to multiply \(\frac{2}{10}\) by 10
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
So,
\(\frac{20}{100}\) + \(\frac{15}{100}\)
= \(\frac{20 + 15}{100}\)
= \(\frac{35}{100}\)
The representation of \(\frac{35}{100}\) in the decimal form is: 0.35
Hence from the above,
We can conclude that
\(\frac{2}{10}\) + \(\frac{15}{100}\) = \(\frac{35}{100}\)
The representation of \(\frac{35}{100}\) in the decimal for is: 0.35
Question 4.
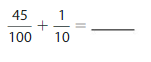
Answer:
The representation of the sum in the fraction form is:
\(\frac{1}{10}\) + \(\frac{45}{100}\) = \(\frac{55}{100}\)
The representation of \(\frac{55}{100}\) in the decimal for is: 0.55
Explanation:
The given fractions are: \(\frac{45}{100}\) and \(\frac{1}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{1}{10}\) as the hundredths, we have to multiply \(\frac{1}{10}\) by 10
So,
The representation of \(\frac{1}{10}\) as hundredths in the fraction form is: \(\frac{10}{100}\)
So,
\(\frac{10}{100}\) + \(\frac{45}{100}\)
= \(\frac{10 + 45}{100}\)
= \(\frac{55}{100}\)
The representation of \(\frac{55}{100}\) in the decimal form is: 0.55
Hence from the above,
We can conclude that
\(\frac{1}{10}\) + \(\frac{45}{100}\) = \(\frac{55}{100}\)
The representation of \(\frac{55}{100}\) in the decimal for is: 0.55
Question 5.
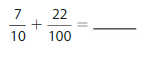
Answer:
The representation of the sum in the fraction form is:
\(\frac{7}{10}\) + \(\frac{22}{100}\) = \(\frac{92}{100}\)
The representation of \(\frac{92}{100}\) in the decimal for is: 0.92
Explanation:
The given fractions are: \(\frac{22}{100}\) and \(\frac{7}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{7}{10}\) as the hundredths, we have to multiply \(\frac{7}{10}\) by 10
So,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
So,
\(\frac{70}{100}\) + \(\frac{22}{100}\)
= \(\frac{70 + 22}{100}\)
= \(\frac{92}{100}\)
The representation of \(\frac{92}{100}\) in the decimal form is: 0.92
Hence from the above,
We can conclude that
\(\frac{7}{10}\) + \(\frac{22}{100}\) = \(\frac{92}{100}\)
The representation of \(\frac{92}{100}\) in the decimal for is: 0.92
Question 6.
Answer:
The representation of the sum in the fraction form is:
\(\frac{5}{10}\) + \(\frac{17}{100}\) = \(\frac{67}{100}\)
The representation of \(\frac{67}{100}\) in the decimal for is: 0.67
Explanation:
The given fractions are: \(\frac{17}{100}\) and \(\frac{5}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{5}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) by 10
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{50}{100}\) + \(\frac{17}{100}\)
= \(\frac{50 + 17}{100}\)
= \(\frac{67}{100}\)
The representation of \(\frac{67}{100}\) in the decimal form is: 0.67
Hence from the above,
We can conclude that
\(\frac{5}{10}\) + \(\frac{17}{100}\) = \(\frac{67}{100}\)
The representation of \(\frac{67}{100}\) in the decimal for is: 0.67
Question 7.
0.6 + 0.25 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{6}{10}\) + \(\frac{25}{100}\) = \(\frac{85}{100}\)
The representation of 0.25 + 0.6 in the decimal form is: 0.85
Explanation:
The given decimal numbers are: 0.6 and 0.25
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{25}{100}\) and \(\frac{6}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{6}{10}\) as the hundredths, we have to multiply \(\frac{6}{10}\) by 10
So,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
So,
\(\frac{60}{100}\) + \(\frac{25}{100}\)
= \(\frac{60 + 25}{100}\)
= \(\frac{85}{100}\)
The representation of \(\frac{85}{100}\) in the decimal form is: 0.85
Hence from the above,
We can conclude that
\(\frac{6}{10}\) + \(\frac{25}{100}\) = \(\frac{85}{100}\)
The representation of \(\frac{85}{100}\) in the decimal for is: 0.85
Question 8.
0.3 + 0.40 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{3}{10}\) + \(\frac{40}{100}\) = \(\frac{70}{100}\)
The representation of 0.40 + 0.3 in the decimal form is: 0.70
Explanation:
The given decimal numbers are: 0.3 and 0.40
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{40}{100}\) and \(\frac{3}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{3}{10}\) as the hundredths, we have to multiply \(\frac{3}{10}\) by 10
So,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
So,
\(\frac{30}{100}\) + \(\frac{40}{100}\)
= \(\frac{30 + 40}{100}\)
= \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
Hence from the above,
We can conclude that
\(\frac{3}{10}\) + \(\frac{40}{100}\) = \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal for is: 0.70
Question 9.
0.05 + 0.9 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{9}{10}\) + \(\frac{5}{100}\) = \(\frac{95}{100}\)
The representation of 0.05 + 0.9 in the decimal form is: 0.95
Explanation:
The given decimal numbers are: 0.05 and 0.9
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{5}{100}\) and \(\frac{9}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{9}{10}\) as the hundredths, we have to multiply \(\frac{9}{10}\) by 10
So,
The representation of \(\frac{9}{10}\) as hundredths in the fraction form is: \(\frac{90}{100}\)
So,
\(\frac{5}{100}\) + \(\frac{90}{100}\)
= \(\frac{5 + 90}{100}\)
= \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal form is: 0.95
Hence from the above,
We can conclude that
\(\frac{9}{10}\) + \(\frac{5}{100}\) = \(\frac{95}{100}\)
The representation of \(\frac{95}{100}\) in the decimal for is: 0.95
Find the sum.
Question 10.
Answer:
The representation of the sum in the fraction form is:
\(\frac{41}{100}\) + \(\frac{22}{100}\) + \(\frac{3}{10}\) = \(\frac{93}{100}\)
The representation of \(\frac{93}{100}\) in the decimal for is: 0.93
Explanation:
The given fractions are: \(\frac{41}{100}\), \(\frac{22}{100}\) and \(\frac{3}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{3}{10}\) as the hundredths, we have to multiply \(\frac{3}{10}\) by 10
So,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
So,
\(\frac{41}{100}\) + \(\frac{22}{100}\) + \(\frac{30}{100}\)
= \(\frac{41 + 22 + 30}{100}\)
= \(\frac{93}{100}\)
The representation of \(\frac{93}{100}\) in the decimal form is: 0.93
Hence from the above,
We can conclude that
\(\frac{3}{10}\) + \(\frac{41}{100}\) + \(\frac{22}{100}\) = \(\frac{93}{100}\)
The representation of \(\frac{93}{100}\) in the decimal for is: 0.93
Question 11.
0.8 + 0.25 + 0.75 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{8}{10}\) + \(\frac{75}{100}\) + \(\frac{25}{100}\) = \(\frac{180}{100}\)
The representation of 0.25 + 0.75 + 0.8 in the decimal for is: 1.80
Explanation:
The given decimal numbers are: 0.8, 0.75 and 0.25
So, convert the three decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{25}{100}\) , \(\frac{8}{10}\) and \(\frac{75}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{8}{10}\) as the hundredths, we have to multiply \(\frac{}{10}\) by 10
So,
The representation of \(\frac{8}{10}\) as hundredths in the fraction form is: \(\frac{80}{100}\)
So,
\(\frac{80}{100}\) + \(\frac{25}{100}\) + \(\frac{75}{100}\)
= \(\frac{80 + 25 + 75}{100}\)
= \(\frac{180}{100}\)
The representation of \(\frac{180}{100}\) in the decimal form is: 1.80
Hence from the above,
We can conclude that
\(\frac{8}{10}\) + \(\frac{25}{100}\) + \(\frac{75}{100}\) = \(\frac{180}{100}\)
The representation of \(\frac{180}{100}\) in the decimal for is: 1.80
Question 12.
Patterns
Describe and complete the pattern.
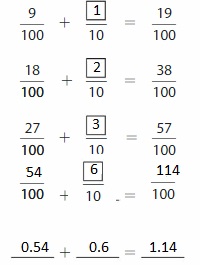
Answer:
The representation of the sum in the fraction form is:
\(\frac{1}{10}\) + \(\frac{9}{100}\) = \(\frac{19}{100}\)
The representation of \(\frac{19}{100}\) in the decimal for is: 0.19
The representation of the sum in the fraction form is:
\(\frac{2}{10}\) + \(\frac{18}{100}\) = \(\frac{38}{100}\)
The representation of \(\frac{38}{100}\) in the decimal for is: 0.38
The representation of the sum in the fraction form is:
\(\frac{3}{10}\) + \(\frac{27}{100}\) = \(\frac{57}{100}\)
The representation of \(\frac{114}{100}\) in the decimal for is: 0.57
Now,
Whwn we add all the three results, we will get
The last result’s representation in the fraction form is:
\(\frac{19}{100}\) + \(\frac{38}{100}\) + \(\frac{57}{100}\) = \(\frac{114}{100}\)
The last result’s representation in the decimal form is:
0.19 + 0.38 + 0.57 = 1.14
Question 13.
Which One Doesn’t Belong? Which expression does not belong with the other three?

Answer:
Let the Expressions be named as A, B, C, and D
The given expressions are:

From the above expressions, Expression D does not belong with the other three
Explanation:
Let the expressions be named A, B, C, and D
So,
The expressions are:

So, from the above expressions,
We can observe that the Expression D does not belong with the other three
Question 14.
Modeling Real Life
In an aquarium, \(\frac{5}{10}\) of the fish are red and \(\frac{3}{100}\) of the fish are yellow. What fraction of the fish is more?
Answer: The fraction of the fish that is red is more in the aquarium
Explanation:
It is given that in the aquarium,
There are \(\frac{5}{10}\) of the fish are red and \(\frac{3}{100}\) of the fish are yellow.
So, for comparison, we have to equal the denominators
So,
\(\frac{5}{10}\) has to be multiplied by 10 to make the denominator of \(\frac{5}{10}\) as hundredths
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So, when we compare the fishes that are red and yellow,
We will get that
Red fishes > Yellow fishes
hence, from the above,
We can conclude that the red fishes are more than yellow fishes in the aquarium
Question 15.
DIG DEEPER!
Which gecko is longer? Explain.

Answer: Leopard Gecko is longer
Explanation:
It is given that
The total length of Leopard Gecko is: 0.05 + 0.06 = 0.11 m = \(\frac{11}{100}\)
The length of Adult Electric Blue Gecko is: \(\frac{7}{100}\)
So, from the above,
We can say that the numerators of both the fractions are equal.
So, when we compare,
We can see that leopard gecko is longer than adult Electric Blue Gecko
Hence, from the above,
We can conclude that the Leopard Gecko is longer than the Adult Electric Blue Gecko
Review & Refresh
Question 16.
38 ÷ 4
Answer: 38 ÷ 4 = 9 R 2
Explanation:
By using the partial quotients method,
38 ÷ 4 = ( 32 + 4 ) ÷ 4
= ( 32 ÷ 4 ) + ( 4 ÷ 4 )
= 8 + 1
= 9 R 2
Hence, 38 ÷ 4 = 9 R 2
Question 17.
641 ÷ 9
Answer: 641 ÷ 9 = 71 R 2
Explanation:
By using the partial quotients method,
641 ÷ 9 = ( 630 + 9 ) ÷ 9
= ( 630 ÷ 9 ) + ( 9 ÷ 9 (
= 70 + 1
= 71 R 2
Hence, 641 ÷ 9 = 71 R 2
Question 18.
52 ÷ 7
Answer: 52 ÷ 7 = 7 R 3
Explanation:
By using the partial quotients method,
52 ÷ 7 = (42 + 7 ) ÷ 7
= ( 42 ÷ 7 ) + ( 7 ÷ 7 )
= 6 + 1
= 7 R 3
Hence, 52 ÷ 7 = 7 R 3
Lesson 10.6 Fractions, Decimals and Money
Explore and Grow
Shade the model to show each money moment.
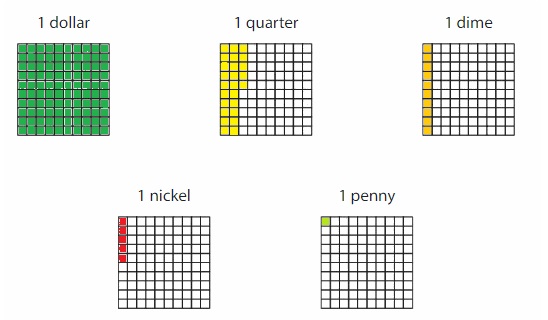
Answer: Here, we have taken the reference of 1 dollar and find out the amount by them that is equal to 1 dollar
Explanation:
We know that,
1 Quarter = 0.25 dollar
1 dime = 0.1 dollar
1 nickel = 0.05 dollar
1 penny = 0.01 dollar
Hence, the above values are marked in the above-given model.
Reasoning
How can you write each money amount as a fraction and a decimal in terms of dollars?
Answer:
The representation of the Quarter, in the dollar in the fraction form is: \(\frac{25}{100}\) dollar
The representation of the Quarter, in the dollar in the decimal form is: 0.25
The representation of the dime, in the dollar in the fraction form is: \(\frac{10}{100}\) dollar
The representation of the dime, in the dollar in the decimal form is: 0.10
The representation of the nickel, in the dollar in the fraction form is: \(\frac{5}{100}\) dollar
The representation of the nickel, in the dollar in the decimal form is: 0.05
The representation of the penny, in the dollar in the fraction form is: \(\frac{1}{100}\) dollar
The representation of the penny, in the dollar in the decimal form is: 0.01
Explanation:
We know that,
1 Quarter = 0.25 dollar
1 dime = 0.1 dollar
1 nickel = 0.05 dollar
1 penny = 0.01 dollar
So, all the money moments are represented in the terms of dollars.
So, the representation of all the money moments in terms of dollars in the fraction and the decimal forms is:
The representation of the Quarter, in the dollar in the fraction form is: \(\frac{25}{100}\) dollar
The representation of the Quarter, in the dollar in the decimal form is: 0.25
The representation of the dime, in the dollar in the fraction form is: \(\frac{10}{100}\) dollar
The representation of the dime, in the dollar in the decimal form is: 0.10
The representation of the nickel, in the dollar in the fraction form is: \(\frac{5}{100}\) dollar
The representation of the nickel, in the dollar in the decimal form is: 0.05
The representation of the penny, in the dollar in the fraction form is: \(\frac{1}{100}\) dollar
The representation of the penny, in the dollar in the decimal form is: 0.01
Think and Grow: Fractions, Decimals, and Money
You can use a dollar sign and a decimal point to write a money amount. Just as a decimal point separates ones from tenths and hundredths, it also separates whole dollars from cents.

Use the total money amount to complete the table.
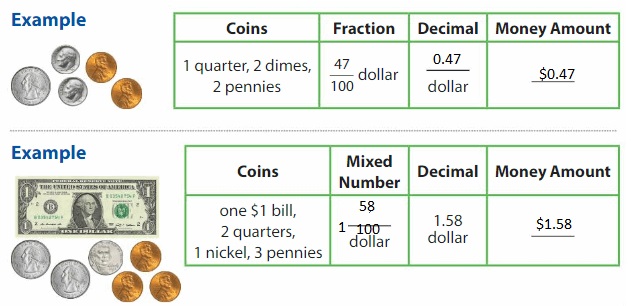
Show and Grow
Find the total money amount. Then write the amount as a fraction or mixed number and as a decimal.
Question 1.

Answer: The total amount of money is: $0.66
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 penny = $0.01
The given money is: 2 Quarters, 3 nickels, and 1 penny
So,
The total amount of money = ( 2 × 0.25 ) + ( 3 × 0.05 ) + ( 1 × 0.01 )
= 0.50 + 0.15 + 0.01
= 0.06
Hence,
The total amount of money is: $0.06
The representation of $0.06 in the fraction form is: \(\frac{6}{100}\) dollar
The representation of $0.06 in the decimal form is: $0.06
Question 2.

Answer: The total amount of money is: $2.30
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
The given money is: 2 dollars, 1 Quarter, and 1 nickel
So,
The total amount of money = ( 2 × 1 ) + ( 1 × 0.25 ) + ( 1 × 0.05 )
= 2 + 0.25 + 0.05
= 2.30
Hence,
The total amount of money is: $2.30
The representation of $2.30 in the fraction form is: 2\(\frac{30}{100}\) dollar
The representation of $2.30 in the decimal form is: $2.30
Apply and Grow: Practice
Find the total money amount. Then write the amount as a fraction or mixed number and as a decimal.
Question 3.
Answer: The total amount of money is: $0.46
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 dime = $0.10
1 penny = $0.01
The given money is: 6 pennies, 1 Quarter, 1 dime, and 1 nickel
So,
The total amount of money = ( 6 × 0.01 ) + ( 1 × 0.25 ) + ( 1 × 0.05 ) + ( 1 × 0.10 )
= 0.06 + 0.25 + 0.05 + 0.10
= 0.46
Hence,
The total amount of money is: $0.46
The representation of $0.46 in the fraction form is: \(\frac{46}{100}\) dollar
The representation of $0.46 in the decimal form is: $0.46
Question 4.

Answer: The total amount of money is: $0.46
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
4 Quarters = 1 dollar
The given money is: 4 Quarters, 1 dollar, and 1 nickel
So,
The total amount of money = ( 1 × 1 ) + ( 4 × 0.25 ) + ( 1 × 0.05 )
= 1 + 1 + 0.05
= 2.05
Hence,
The total amount of money is: $2.05
The representation of $2.05 in the fraction form is: 2\(\frac{5}{100}\) dollar
The representation of $2.05 in the decimal form is: $2.05
Write the fraction or mixed number as a money amount and as a decimal.
Question 5.
\(\frac{53}{100}\)
Answer: The representation of \(\frac{53}{100}\) as the total amount of money is: $0.53
Explanation:
The given fraction is: \(\frac{53}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.53
Question 6.
\(\frac{4}{100}\)
Answer: The representation of \(\frac{4}{100}\) as the total amount of money is: $0.04
Explanation:
The given fraction is: \(\frac{4}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.04
Question 7.
\(\frac{100}{100}\)
Answer: The representation of \(\frac{100}{100}\) as the total amount of money is: $1
Explanation:
The given fraction is: \(\frac{100}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $1
Question 8.
1\(\frac{22}{100}\)
Answer: The representation of 1\(\frac{22}{100}\) as the total amount of money is: $1.22
Explanation:
The given fraction is: 1\(\frac{22}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $1.22
Question 9.
1\(\frac{18}{100}\)
Answer: The representation of 1\(\frac{18}{100}\) as the total amount of money is: $1.18
Explanation:
The given fraction is: 1\(\frac{18}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $1.18
Question 10.
1\(\frac{70}{100}\)
Answer: The representation of 1\(\frac{70}{100}\) as the total amount of money is: $1.70
Explanation:
The given fraction is: 1\(\frac{70}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $1.70
Question 11.
You find 1 dime, 3 nickels, and 2 pennies on the ground. How much money do you find? Write your answer in three different ways.
Answer: The total amount of money you find on the ground is: $0.27
Explanation:
The given amount that you find on the ground is: 1 dime, 3 nickels, and 2 pennies
We know that,
1 dime = 0.10 dollars
1 nickel = $0.05 dollars
1 penny = $0.01 dollars
So,
The total amount of money you find on the ground = ( 1 × 0.10 ) + ( 3 × 0.05 ) + (2 × 0.01 )
= 0.10 + 0.15 + 0.02
= 0.27
Hence from the above,
We can conclude that the three ways of representing the total amount of money is:
The total amount of money you find on the ground is: $0.27
The representation of the total amount of money in the fraction form is: \(\frac{27}{100}\) dollar
The representation of the total amount of money in the decimal form is: $0.27
Question 12.
YOU BE THE TEACHER
Your friend has three $1 bills and 2 pennies. Your friend writes, “I have $ 3.2.” Is your friend correct? Explain.
Answer: No, your friend is wrong
Explanation:
It is given that your friend has three $1 bills and 2 pennies.
So,
The given amount your friend has: 3 $1 bills and 2 pennies
We know that,
1 penny = 0.01 dollars
So,
The total amount of money your friend has = ( 3 × 1 ) + ( 2 × 0.01 )
= 3 + 0.02
= 3.02
Hence,
The total amount of money your friend has: $3.02 dollars or 3 dollars and 2 pennies
But, your friend has written $3.02 as $3.20 which means 3 dollars and 2 dimes
Hence, from the above,
We can conclude that your friend is wrong
Question 13.
DIG DEEPER!
You have \(\frac{1}{4}\) dollar in coins. Draw two possible groups of coins that you could have.
Answer: The possible group of coins that you could have for \(\frac{1}{4}\) is: Quarter
Explanation:
It is given that you have \(\frac{1}{4}\) dollar in coins.
But, we have al, the money moments in terms of 100.
So, to make the denominator of \(\frac{1}{4}\) 100, multiply \(\frac{1}{4}\) by 25
So,
The representation of \(\frac{1}{4}\) as hundredths in the fraction form is: \(\frac{25}{100}\)
We know that,
1 Quarter = $0.25
Hence, from the above,
We can conclude that the possible group of coins that you could have for \(\frac{1}{4}\) is: Quarter
Think and Grow: Modeling Real Life
Example
Newton has \(\frac{85}{100}\) dollar. Can he buy the spinning toy? Explain.

Write the fraction as a money amount.
\(\frac{85}{100}\) as a money amount is $0.85.
Compare the amount of money Newton has to the price of the toy.
Newton can’t buy the spinning toy.
Explanation:
It is given that Newton has \(\frac{85}{100}\) dollar
So,
The amount of money that Newton has in the decimal form is: $0.85
But, it is also given that
The cost of spinning toy is: \(\frac{99}{100}\) dollar
So, for comparison, we have to make either the numerators or the denominators equal.
Here, both the denominators are equal.
So, we can compare both the fractions directly.
So, by comparing, we get,
0.85 < 0.99
Hence,
We can conclude that Newton can’t buy the spinning toy.
Show and Grow
Question 14.
Descartes has \(\frac{76}{100}\) dollar. Can he buy the bouncy ball? Explain.

Answer: Yes, he can buy the bouncy ball
Explanation:
It is given that Descartes has \(\frac{76}{100}\) dollar
So,
The amount of money that Descartes has in the decimal form is: $0.76
But, it is also given that
The cost of bouncy ball is: \(\frac{50}{100}\) dollar
So, for comparison, we have to make either the numerators or the denominators equal.
Here, both the denominators are equal.
So, we can compare both the fractions directly.
So, by comparing, we get,
0.76 > 0.50
Hence,
We can conclude that Descartes can buy the bouncy ball.
Question 15.
You throw 3 dimes, 3 nickels, and 8 pennies into a fountain. Your friend throws 1 quarter, 4 nickels, and 5 pennies. Who throws a greater amount of money into the fountain?
Answer: You throw a greater amount of money into the fountain when compared to your friend.
Explanation:
It is given that you throw 3 dimes, 3 nickels, and 8 pennies and your friend throws 1 quarter, 4 nickels, and 5 pennies
So,
The amount that you have is: 3 dimes, 3 nickels, and 8 pennies
The amount that your friend has is: 1 quarter, 4 nickels, and 5 pennies
We know that,
1 quarter = $0.25
1 dime = $0.10
1 nickel = $0.05
1 penny = $0.01
So,
The total amount of money you have = ( 3 × 0.10 ) + ( 3 × 0.05 ) + ( 8 × 0.01 )
= 0.30 + 0.15 + 0.08
= $0.53
The total amount of money your friend has = ( 1 × 0.25 ) + ( 4 × 0.05 ) + ( 5 × 0.01 )
= 0.25 + 0.20 + 0.05
= $0.50
Now,
The representation of the amount of money you have in the fraction form is: \(\frac{53}{100}\) dollars
The representation of the amount of money your friend has in the fraction form is: \(\frac{50}{100}\) dollars
So, by comparing these two amounts,
We can conclude that you have a greater amount of money than your friend
Question 16.
DIG DEEPER!
Complete the table. Which piggy bank has the greatest amount of money? the least amount of money?
Answer:
The piggy bank which has the greatest amount of money is: B
the piggy bank which has the least amount of money is: C
Explanation:
The given table is:

From the given table,
The amount of money present in all the three piggy banks is: Quarters, Dimes, Nickels, and pennies
We know that,
1 Quarter = $0.25
1 dime = $0.10
1 nickel = $0.05
1 penny = $0.01
So,
The total amount of money that all the three piggy banks have:
A: ( 3 × 0.25 ) + ( 1 × 0.10 ) + ( 4 × 0.05 ) + ( 2 × 0.01 ) = $1.07
B: ( 1 × 0.25 ) + ( 7 × 0.10 ) + ( 3 × 0.05 ) + ( 0 × 0.01 ) = $1.10
C: ( 2 × 0.25 ) + ( 0 × 0.10 ) + ( 8 × 0.05 ) + ( 11 × 0.01 ) = $1.01
Hence, from the above,
we can conclude that
The piggy bank that has the greatest amount of money is: B
The piggy bank that has the least amount of money is: C
Fractions, Decimals and Money Homework & Practice 10.6
Write the money amount as a fraction or mixed number and as a decimal.
Question 1.
$ 0.53
Answer: The representation of $0.53 as the total amount of money in the fraction form is: \(\frac{53}{100}\) dollar
Explanation:
The given amount of money in the decimal form is: $0.53
The given decimal form will be given as an amount in dollars.
So,
The total amount of money in the fraction form is: \(\frac{53}{100}\) dollars
The total amount of money in the decimal form is: $0.53
Question 2.
$ 0.40
Answer: The representation of $0.40 as the total amount of money in the fraction form is: \(\frac{40}{100}\) dollar
Explanation:
The given amount of money in the decimal form is: $0.40
The given decimal form will be given as an amount in dollars.
So,
The total amount of money in the fraction form is: \(\frac{40}{100}\) dollars
The total amount of money in the decimal form is: $0.40
Question 3.
$1.01
Answer: The representation of $1.01 as the total amount of money in the fraction form is: 1\(\frac{1}{100}\) dollar
Explanation:
The given amount of money in the decimal form is: $1.01
The given decimal form will be given as an amount in dollars.
So,
The total amount of money in the fraction form is: 1\(\frac{1}{100}\) dollars
The total amount of money in the decimal form is: $1.01
Find the total money amount. Then write the amount as a fraction or mixed number and as a decimal.
Question 4.

Answer: The total amount of money is: $0.65
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 dime = $0.10
The given money is: 1 Quarter, 2 dimes, and 4 nickel
So,
The total amount of money = ( 1 × 0.25 ) + ( 4 × 0.05 ) + ( 2 × 0.10 )
= 0.25 + 0.20 + 0.20
= 0.65
Hence,
The total amount of money is: $0.65
The representation of $0.65 in the fraction form is: \(\frac{65}{100}\) dollar
The representation of $0.65 in the decimal form is: $0.65
Question 5.

Answer: The total amount of money is: $2.13
Explanation:
We know that,
1 dime = $0.10
1 penny = $0.01
The given money is: 3 pennies, 1 dime, and 2 dollars
So,
The total amount of money = ( 3 × 0.01 ) + ( 2 × 1 ) + ( 1 × 0.10 )
= 0.03 + 2 + 0.10
= 2.13
Hence,
The total amount of money is: $2.13
The representation of $2.13 in the fraction form is: 2\(\frac{13}{100}\) dollar
The representation of $2.13 in the decimal form is: $2.13
Question 6.
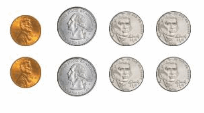
Answer: The total amount of money is: $0.92
Explanation:
We know that,
1 Quarter = $0.25
1 dime = $0.10
1 penny = $0.01
The given money is: 2 pennies, 2 Quarters, 4 dimes
So,
The total amount of money = ( 2 × 0.01 ) + ( 2 × 0.25 ) + ( 4 × 0.10 )
= 0.02 +0.50 + 0.40
= 0.92
Hence,
The total amount of money is: $0.92
The representation of $0.92 in the fraction form is: \(\frac{92}{100}\) dollar
The representation of $0.92 in the decimal form is: $0.92
Question 7.

Answer: The total amount of money is: $3.15
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 dime = $0.10
The given money is: 4 Quarters, 2 dollars, 1 dime, and 1 nickel
So,
The total amount of money = ( 2 × 1 ) + ( 4 × 0.25 ) + ( 1 × 0.05 ) + ( 1 × 0.10 )
= 2 + 1 + 0.05 + 0.10
= 3.15
Hence,
The total amount of money is: $3.15
The representation of $3.15 in the fraction form is: 3\(\frac{15}{100}\) dollar
The representation of $3.15 in the decimal form is: $3.15
Write the fraction or mixed number as a money amount and as a decimal.
Question 8.
\(\frac{87}{100}\)
Answer: The representation of \(\frac{87}{100}\) as the total amount of money is: $0.87
Explanation:
The given fraction is: \(\frac{87}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.87
Question 9.
\(\frac{12}{100}\)
Answer: The representation of \(\frac{12}{100}\) as the total amount of money is: $0.12
Explanation:
The given fraction is: \(\frac{12}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.12
Question 10.
1\(\frac{9}{100}\)
Answer: The representation of 1\(\frac{9}{100}\) as the total amount of money is: $1.09
Explanation:
The given fraction is: 1\(\frac{9}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $1.09
Question 11.
You find 3 quarters, 2 nickels, and 1 penny in your backpack. How much money do you find? Write your answer in three different ways.
Answer: The amount of money you find is: $0.86
Explanation:
It is given that you find 3 quarters, 2 nickels, and 1 penny in your backpack
So,
The amount of money you have is: 3 quarters, 2 nickels, and 1 penny
We know that,
1 quarter = $0.25
1 nickel = $0.05
1 penny = $0.01
So,
The total amount of money you have = ( 3 × 0.25 ) + ( 2 × 0.05 ) + ( 1 × 0.01 )
= 0.75 + 0.10 + 0.01
= 0.86
Hence,
The total amount of money you have is: $0.86
The total amount of money you have in the fraction form is: \(\frac{86}{100}\)
The total amount of money you have in the decimal form is: $0.86
Question 12.
Which One Doesn’t Belong? Which one does not belong with the other three?
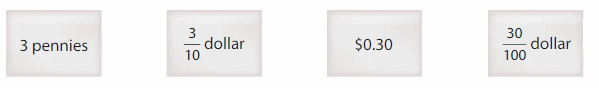
Answer:
Let the amounts be named A, B, C, and D
So, from the amounts,
we can say that A) does not belong to the other three.
Explanation:
Le the amounts named as A, B, C, and D
Now,
A) 3 pennies B) \(\frac{3}{10}\) C) 0.30 dollars D) \(\frac{30}{100}\)
We know that,
1 penny = $0.01
So,
3 pennies = $0.03
Hence, from the above,
we can conclude that A) does not belong to the other three.
Question 13.
Reasoning
Would you rather have \(\frac{2}{10}\) of a dollar or 6 nickels? Explain.
Answer: You would rather have 6 nickels
Explanation:
The given fraction is: \(\frac{2}{10}\) of a dollar
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
The representation of \(\frac{20}{100}\) in the decimal form is: 0.20
We know that,
1 nickel = $0.05
So,
6 nickels = 6 × 0.05 = $0.30
Now,
When we compare the given fraction and 6 nickels, w can observe that
6 nickels > \(\frac{2}{10}\) of a dollar
Hence, from the above,
we can conclude that you would have to rather have 6 nickels than \(\frac{2}{10}\) of a dollar
Question 14.
Modeling Real Life
Newton has \(\frac{46}{100}\) dollar. Can he buys the key chain ? Explain.

Answer: No, Newton can’t buy the key chain
Explanation:
It is given that Newton has \(\frac{46}{10}\) dollar
So,
The representation of \(\frac{46}{10}\) in the decimal form is: $0.46
It is also given that,
The cost of the key chain is: $0.49
Now,
When we compare the fractions, we have to equate either the numerators or the denominators.
Here, both the denominators are equal.
So,
When we compare, we will observe
0.46 < 0.49
Hence, from the above,
We can conclude that Newton can’t buy the key chain
Question 15.
DIG DEEPER!
Descartes has $1. Can he buy 2 key chains? Explain how you know without calculating.
Answer: Yes, Descartes can buy 2 key chains
Explanation:
From the above problem,
The cost of 1 key chain is: $0.49
It is given that Descartes has $1 and he wants to buy the 2 key chains
So,
The cost of 2 key chains = 0.49 + 0.49 = $0.98
But, Descartes has $1
So,
The money that Descartes left = 1 – 0.98 = 0.02
Hence, from the above,
We can conclude that Descartes can buy the 2 key chains
Review & Refresh
Add.
Question 16.
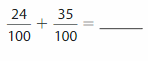
Answer: \(\frac{24}{100}\) + \(\frac{35}{100}\) = \(\frac{59}{100}\)
Explanation:
The given fractions are: \(\frac{24}{100}\) and \(\frac{35}{100}\)
So, for the addition of the fractions, we have to equate either both the numerators or both the denominators.
Here, both the denominators are equal.
Hence,
\(\frac{24}{100}\) + \(\frac{35}{100}\) = \(\frac{59}{100}\)
Question 17.
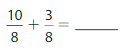
Answer: \(\frac{10}{8}\) + \(\frac{3}{8}\) = \(\frac{13}{8}\)
Explanation:
The given fractions are: \(\frac{10}{8}\) and \(\frac{3}{8}\)
So, for the addition of the fractions, we have to see whether the denominators are equal or the numerators are equal.
Here, both the denominators are equal.
Hence,
\(\frac{10}{8}\) + \(\frac{3}{8}\) = \(\frac{13}{8}\)
Question 18.
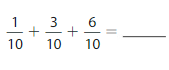
Answer: \(\frac{1}{10}\) + \(\frac{3}{10}\) + \(\frac{6}{10}\) = \(\frac{10}{10}\)
Explanation:
The given fractions are: \(\frac{1}{10}\), \(\frac{3}{10}\) and \(\frac{6}{10}\)
So, in addition,
We have to equate either both the numerators or both the denominators.
Here,
The denominators of all the fractions are equal.
Hence,
\(\frac{1}{10}\) + \(\frac{3}{10}\) + \(\frac{6}{10}\) = \(\frac{10}{10}\)
Lesson 10.7 Operations with Money
Explore and Grow
Draw bills and coins to solve each problem. How much do all of the toys cost?
- You pay for one of the toys with a $10 bill. What is your change?
Answer:
Let the toy be an Action figure.
Now,
It is given that the cost of an Action figure is: $5.50
It is also given that you pay for one of the toys with a $10 bill
So,
Your change = 10 – 5.50 = $4.50
Hence, from the above,
We can conclude that the change is: $4.50
2. You buy three of the same toys. How much do the toys cost in all?
Answer:
The given table is:

From the given table,
The cost of an Action figure is: $5.50
The cost of a whistle is: $1.25
The cost of a Board game is: $3.75
So,
The cost of 3 Action figures = 3 × 5.50 = $16.50
The cost of 3 whistles = 3 × 1.25 = $3.75
The cost of 3 board games = 3 × 3.75 = $11.15
3. You and your friend put your money together to buy some of the toys. The cashier gives you a $4.50 change. You want to share the change equally. How much money does each of you get?
Answer: It is given that you and your friend put your money together to buy some of the toys. It is also given that the cashier gives you a $4.50 change.
So,
The amount that should be shared equally between you and your friend = 4.50 ÷ 2
= (4 ÷ 2 ) + ( 0.50 ÷ 2 )
= 2 + 0.25
= 2.25
Hence, from the above,
we can conclude that the amount that should be shared equally between you and your friend is: $2.25
Precision
Compare your work to your partner’s.
Think and Grow:
Newton has $1.35. Descartes has $1.25. How much money do they have altogether?

Answer:
It is given that Newton has $1.35 and Descartes has $1.25.
So,
The total amount of money they have altogether = $1.35 + $1.25
= $2.60
Hence, from the above,
We can conclude that they have $2.60 altogether.
Example
Newton has $2.45. He spends $1.10. How much money does he have left?

He has $1.35 left.
Example
Three friends each have$0.60. How much money do they have in all?

Answer: It is given that the three friends each have $0.60
So,
the total amount of money that the three friends have = 0.60 × 3 = $1.80
Hence, from the above,
We can conclude that they have $1.80 in all.
Example
You and a friend have a total of $ 1.48. You want to share the money equally. How much money should each of you get?

Answer: It is given that you and a friend have a total of $1.48
It is also given that you want to share the money equally
So,
The amount of money that you and your friend share the money equally = 1.48 ÷ 2
= ( 1 ÷ 2 ) + ( 0.48 ÷ 2 )
= 0.5 + 0.24
= 0.74
Hence, from the above,
We can conclude that you each should get $0.74.
Show and Grow
Question 1.
You pay a total of $2.25 for 3 granola bars. How much money does each bar cost? Draw bills and coins to solve.
Answer: The amount of money does each bar cost is: $0.75
Explanation:
It is given that you pay a total of $2.25 for 3 granola bars
So,
The amount of money that each bar cost = The total cost of 3 granola bars ÷ 3
= 2.25 ÷ 3
= 0.75
Hence, from the above,
We can conclude that the amount of money does each ba cost is: $0.75
Apply and Grow: Practice
Question 2.
You buy 2 stamps. Each stamp costs $0.49. How much money do you spend in all?
Answer: The total amount of money you spend is: $0.98
Explanation:
It is given that you buy 2 stamps and each stamp costs $0.49
So,
The total amount of money you spent on buying stamps = The cost of each stamp × 2
= 0.49 × 2
= $0.98
Hence, from the above,
we can conclude that the amount of money you spent on buying the 2 stamps is: $0.98
Question 3.
Newton has $2.50. He spends $1.07 on a flying disk. How much money does Newton have left?
Answer: The amount of money does Newton have left is: $1.43
Explanation:
It is given that Newton has $2.50 and he spends $1.07 on a flying disk
So,
The amount of money does Newton have left = The amount of money that Newton has – The amount of money that Newton spent
= 2.50 – 107
= $1.43
Hence, from the above,
We can conclude that the amount of money does Newton have left is: $1.43
Question 4.
A tube of toothpaste costs $2.71 and a toothbrush costs $1.62. How much more money does the toothpaste cost more than the toothbrush?
Answer: The amount of money that the toothpaste cost more than the toothbrush is: $1.09
Explanation:
It is given that a tube of toothpaste costs $2.71 and a toothbrush costs $1.62.
So,
The amount of money that the toothpaste cost more than the toothbrush = The cost of toothpaste -The cost of the toothbrush
= 2.71 – 1.62
= $1.07
Hence, from the above,
We can conclude that the more money does the toothpaste cost more than the toothbrush is: $1.07
Question 5.
Two fingerboards cost a total of $7.20. Each fingerboard costs the same amount. How much does each fingerboard cost?

Answer: Each fingerboard costs: 0.36
Explanation:
It is given that the two fingerboards cost a total of $7.20
It is also given that each fingerboard costs the same amount.
So,
The cost of each fingerboard = The cost of 2 fingerboards ÷ 2
= 7.20 ÷ 2
= ( 7 ÷ 2 ) + ( 0.2 ÷ 2 )
= 3.5 + 0.1
= 3.6
Hence, from the above,
We can conclude that the cost of each fingerboard is: $0.36
Question 6.
In Exercise 2, you pay for the stamps using a $1 bill. What is your change?
Answer:
From Exercise 2,
The total cost of buying 2 stamps is: $0.98
In this exercise, it is given that you pay for the stamps using a $1 bill.
So,
The change = 1 – 0.98
= 0.02
Hence, from the above,
We can conclude that The change after paying the $1 bill for paying the stamps is: $0.02
Question 7.
You have four $1 bills and 3 dimes. Do you have enough money to buy the tube of toothpaste and the toothbrush in Exercise 4? Explain.
Answer: No, you don’t have enough money to buy the tube of toothbrush and toothpaste which is explained in Exercise 4
Explanation:
From Exercise 4,
The total cost of money to buy the tube of toothpaste and the toothbrush = 2.71 + 1.62 = $4.33
It is given that you have 4 $1 bills and 3 dimes
We know that,
1 dime = $0.10
So,
The total amount of money you have = (4 × 1 ) + ( 3 × 0.10 )
= 4 + 0.30
= 4.30
Now,
We have to compare 4.33 and 4.30
So, by comparing the 2 values, we will observe
4.33 > 4.30
Hence, from the above,
We can conclude that you don’t have enough money to buy the toothpaste and the toothbrush
Question 8.
DIG DEEPER!
You have $1.10 less than Descartes. How much money do you, Newton, and Descartes have altogether?

Answer:
It is given that you have $1.10 less than Descartes
From the above figure,
Newton has $1.50 and Descartes has $1.25 more than Newton
So,
The amount of money that Descartes has = The amount of money Newton has + 1.25
= 1.50 + 1.25
= $2.75
The amount of money you have = The amount of money Descartes has – 1.10
= 2.75 – 1.10
= $1.65
Hence, from the above,
We can conclude that
The amount of money you have is: $1.65
The amount of money Newton has is: $1.50
The amount of money Descartes has is: $2.75
Think and Grow: Modeling Real Life
Example
You buy a joke book that costs $3.50 and a book about science experiments that costs $4.25. You give the cashier $8. What is your change?
Think: What do you know? What do you need to find? How will you solve?

Step 1: Draw bills and coins to show the money you give the cashier, $8.
Step 2: Subtract the cost of the joke book. Subtract $3.50 by taking away
3 $1 bills and 2 quarters.
The given model is:
Step 3: Subtract the cost of the science experiment book.
Subtract $4.25 by taking away
4 $1 bills and 1 quarter.
Step 4: The remaining coin represents your change.
Your change is $1.75
Show and Grow
Question 9.
You buy a gel pen that costs $1.10 and a school shirt that costs $5.85. You give the cashier $7. What is your change?
Answer: The change is: $0.05
Explanation:
It is given that you buy a gel pen that costs $1.10 and a school shirt that costs $5.85.
So,
The total cost of the gel pen and the school skirt = 5.85 + 1.10 = $ 6.95
It is also given that you give the cashier $7
So,
the change = The money given to the cashier – The total cost of the gel pen and the school skirt
= 7 – 6.95
= 0.05
Hence, from the above,
We can conclude that the change is: $0.05
Question 10.
You have $2.50. Your friend has 2 times as much money as you. How much money do you and your friend have altogether?
Answer: The amount of money you and your friend have altogether is: $7.50
Explanation:
It is given that you have $2.50 and your friend has 2 times as much money as you.
So,
The amount of money your friend has = 2.50 × 2 = $5
So,
The amount of money you and your friend have altogether = The amount of money you have + The amount of money your friend has
= 5 + 2.5
= $7.5
Hence, from the above,
We can conclude that the amount of money you and your friend have altogether is: $7.50
Question 11.
DIG DEEPER!
You have $8.38. Your friend has $3.16. How much money can you give to your friend so that you each have the same amount?
Answer: The amount of money you can give to your friend so that you each have the same amount = $5.22
Explanation:
It is given that you have $8.38 and your friend has $3.16
So,
The amount of money you can give to your friend so that you each have the same amount = The amount of money you have – The amount of money your friend has
= 8.38 – 3.16
= $5.22
Hence, from the above,
We can conclude that the amount of money you can give to your friend so that you each have the same amount is: $5.22
Operations with Money Homework & Practice 10.7
Draw bills and coins to solve.
Question 1.
A sketch pad is $2.85 and a sketching pencil is $1.25. How much more money is the sketch pad than the sketching pencil?
Answer: The amount of money the sketch pad needs more than the sketching pencil is: $1.60
Explanation:
It is given that a sketch pad is $2.85 and a sketching pencil is $1.25.
So,
The cost of a sketch pad is: $2.85
The cost of a sketching pencil is: $1.25
So,
the amount of money more than the sketching pencil = The cost of sketch pad – The cost of the sketching pencil
= 2.85 – 1.25
= $1.60
Hence, from the above,
We can conclude that the amount of money needed more than the sketching pencil is: $.1.60
Question 2.
Descartes buys two toys for a total of $2.54. Each toy costs the same amount. How much does each toy cost?
Answer: The cost of each boy is: $1.27
Explanation:
It is given that Descartes buys 2 toys for a total of $2.54 and it is also given that each toy costs the same amount
So,
The cost of each toy = The total cost of the two toys ÷ 2
= 2.54 ÷ 2
= $1.27
Hence, from the above,
We can conclude that the cost of each toy is: $1.27
Question 3.
You buy 4 bags of the water balloons shown. How much money do you spend in all?

Answer: The total cost of the 4 bags of balloons are: $4.80
Explanation:
It is given that you have 4 bags of balloons and it is also given that the cost of each bag of balloon is $1.20
So,
The total cost of the four bags of balloons = 4 × 1.20
= $4.80
hence, from the above,
We can conclude that the cost of the four bags of balloons is: $4.80
Question 4.
You have four $1 bills and 2 nickels. Do you have enough money to buy the sketch pad and the sketching pencil in Exercise 1? Explain.
Answer: No, we have enough money to buy the sketch pad and the sketching pencil
Explanation:
From Exercise 1,
The total cost of the sketch pen and the sketching pencil = 2.85 + 1.25
= $4.10
In this exercise, it is given that you have 4 $1 bills and 2 nickels.
We know that,
1 nickel = $0.05
So,
The total amount of money = ( 4 × 1 ) + ( 2 × 0.05 )
= + 0.1
= $4.1
So,
The total amount from exercise 1 and the money you have are equal
Hence, from the above,
We can conclude that we have enough money to buy the sketch pen and the sketching pencil
Question 5.
Reasoning
You have 3 jars, with $2.32 in each jar. Do you have enough money to buy the model car? If not, how much more money do you need?

Answer: You don’t have enough money to buy the model car
The amount of money that you needed more to buy the model car is: $0.53
Explanation:
It is given that you have 3 jars, with $2.32 in each jar
So,
The total amount of money n the three jars = 3 × 2.32 = $6.96
It is also given that
The cost of the model car is: $7.49
So,
The amount of money needed more to buy the model car = The cost of the model car – The total amount of money in the three jars
= 7.49 – 6.96
= $0.53
Hence, from the above,
We can conclude that we don’t have enough money to buy the model car
The amount of money needed more to buy the car is: $0.53
Question 6.
DIG DEEPER!
Descartes has 3 quarters, 1 dime, and 3 nickels. He wants to put the same amount of money into each of the two piggy banks. How can he do this with these coins?
Answer: The amount of money in each of the two piggy banks is: $0.5
Explanation:
It is given that Descartes has 3 quarters, 1 dime, and 3 nickels.
So,
The amount of money Descartes possess is: 3 quarters, 1 dime, and 3 nickels
We know that,
1 quarter = $0.25
1 dime = $0.10
1 nickel = $0.05
So,
The total amount of money Descartes possesses = ( 3 × 0.25 ) + ( 1 × 0.10 ) + ( 3 × 0.05 )
= 0.75 + 0.10 + 0.15
= $1.00
So,
The amount of money in each of the two piggy banks = 1 ÷ 2 = $0.5
Hence, from the above,
We can conclude that the amount of money in each of the two piggy banks is: $0.5
Question 7.
Modeling Real Life
You buy the key chains shown. You pay with a $5 bill. What is your change?
Answer: The change is: $1.10
Explanation:
It is given that you have bought some key chains as shown in the below figure.
From the above figure,
The cost of a basketball key chain is: $2.53
The cost of a football chain is: $2.37
So,
The total cost of the two key chains = 2.53 + 2.37
= $4.90
It is also given that you pay with a $5 bill
So,
The change = 5 – The total cost of the key chains
= 5 – 4.90
= $1.10
Hence, from the above,
We can conclude that the change obtained after buying the key chains is: $1.10
Question 8.
DIG DEEPER!
Your class collects pennies and nickels in separate jars. Your class collects $5.87 in pennies and $2.65 in nickels. You divide the total amount of money collected between two charities. How many pennies do you put in the nickel jar so that both jars have the same amount of money?
Answer:
The total amount of money divided between the 2 charities is: $4.26
The number of pennies you need to put in the nickel jar is: $3.22
Explanation:
It is given that your class collects pennies and nickels in separate jars. It is also given that your class collects $5.87 in pennies and $2.65 in nickels.
It is given that you divide the total amount of money collected between two charities.
So,
The total amount of money collected by the class = 5.87 + 2.65 = $8.52
Now,
The total amount of money divided between the 2 charities = 8.52 ÷ 2
= ( 8 ÷ 2 ) + ( 0.52 ÷ 2 )
= 4 + 0.26
= $ 4.26
Now,
The amount of money needed more to add pennies into the nickel jars = 5.87 – 2.65 = $3.22
Hence, from the above,
We can conclude that
The total amount of money divided between the 2 charities is: $4.26
The number of pennies you need to put in the nickel jar is: $3.22
Review & Refresh
Write the product as a multiple of a unit fraction. Then find the product.
Question 9.
![]()
Answer: The product of 6 and \(\frac{7}{12}\) is: \(\frac{14}{4}\)
Explanation:
The given fractions are: \(\frac{6}{1}\) and \(\frac{7}{12}\)
For multiplication,
Multiply numerators and denominators separately.
So,
\(\frac{6}{1}\) × \(\frac{7}{12}\) = \(\frac{6 × 7 }{1 × 12}\)
= \(\frac{42}{12}\)
For the simplified form of \(\frac{42}{12}\), divide \(\frac{42}{12}\) by 3 as 42 and 12 are the multiples of 3
Hence,
\(\frac{7}{12}\) × \(\frac{6}{1}\) = \(\frac{42}{12}\) = \(\frac{14}{4}\)
Question 10.
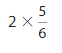
Answer: The product of 2 and \(\frac{5}{6}\) is: \(\frac{5}{3}\)
Explanation:
The given fractions are: \(\frac{2}{1}\) and \(\frac{5}{6}\)
For multiplication,
Multiply numerators and denominators separately.
So,
\(\frac{2}{1}\) × \(\frac{5}{6}\) = \(\frac{2 × 5 }{1 × 6}\)
= \(\frac{10}{6}\)
For the simplified form of \(\frac{10}{6}\), divide \(\frac{10}{6}\) by 2 as 10 and 6 are the multiples of 2
Hence,
\(\frac{5}{6}\) × \(\frac{2}{1}\) = \(\frac{10}{6}\) = \(\frac{5}{3}\)
Question 11.
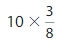
Answer: The product of 10 and \(\frac{3}{8}\) is: \(\frac{15}{4}\)
Explanation:
The given fractions are: \(\frac{10}{1}\) and \(\frac{3}{8}\)
For multiplication,
Multiply numerators and denominators separately.
So,
\(\frac{10}{1}\) × \(\frac{3}{8}\) = \(\frac{10 × 3 }{1 × 8}\)
= \(\frac{30}{8}\)
For the simplified form of \(\frac{30}{8}\), divide \(\frac{30}{8}\) by 2 as 30 and 8 are the multiples of 2
Hence,
\(\frac{5}{8}\) × \(\frac{10}{1}\) = \(\frac{30}{8}\) = \(\frac{15}{4}\)
Relate Fractions and Decimals Performance Task 10
You have a recipe to make one loaf of home made whole wheat bread. You want to make 8 loaves of bread.
1. You need between 6.5 cups and 7 cups of whole wheat flour for one loaf of bread.
a. So far, you measure 3\(\frac{1}{4}\) cups of flour for one loaf. What is the least amount of cups you need to add?

Answer: The least amount of cups you need to add is: 3.25
Explanation:
It is given that you need between 6.5 and 7 cups of whole wheat flour for one loaf of bread.
It is given that you measured so far 3\(\frac{1}{4}\) cups of flour for one loaf
So,
The least number of cups you need to add to make one loaf of bread = 6.5 – 3\(\frac{1}{4}\)
The representation of 3\(\frac{1}{4}\) in the decimal form is: 3.25
So,
The least number of cups you need = 6.5 – 3.25 = 3.25 cups
Hence, from the above,
We can conclude that you need a minimum of 3.25 cups of wheat flour to make a loaf of bread
b. There are about 4 cups of flour in 1 pound. How many 5-pound bags of whole wheat flour should you buy to make all of the bread?

Answer: You should buy about 20 cups of flour to make all the bread
Explanation:
It is given that we need about 4 cups of flour in 1 pound.
So,
The number of cups you need for five-pound bags = 4 × 5 = 20 cups
Hence, from the above,
We can conclude that we will need about 20 cups of flour to make all the bread
c. You use a $10 bill to buy enough bags of whole wheat flour for 8 loaves. What is your change?
Answer: Your change is: $4.8
Explanation:
It is given that you use a $10 bill to buy enough bags of whole wheat flour for 8 loaves.
So,
The total cost of wheat flour = 2.69 × 2 = $5.38
So,
Your change = 10 – 5.38 = $4.62
Hence, from the above,
We can conclude that the change is: $4.62
Question 2.
You need to add 2\(\frac{1}{4}\) cups of warm water for one loaf of bread. The temperature of the water should be about 110°F.
a. How many cups of water do you need for all of the bread?
Answer: The number of cups of warm water you need for all the bread is: 18 cups
Explanation:
It is given that you need to add 2\(\frac{1}{4}\) cups of warm water for one loaf of bread.
But, it is given for the whole read, there are 8 loaves of bread.
So,
The total number of cups you need to make all the bread = 2\(\frac{1}{4}\) × 8
= 2.25 × 8
= 18 cups
Hence, from the above,
We can conclude that we will need 18 cups of warm water to make all the whole bread
b. You find the temperatures of 3 different samples of water. Which sample of water should you use? Explain.
Answer: We will use a C sample of water
Explanation:
The given temperatures are:

From the above table,
The temperature of A is: 105.5
The temperature of B is: 114.4
The temperature of C is: 109.6
It is given that the temperature to make the bread is: 110
So,
We will choose sample C to make the bread.
Hence, from the above,
we can conclude that we will use C’s sample of water to make the bread
Relate Fractions and Decimals Activity
Decimal Boss
Directions:
- Divide the Decimal Boss Cards equally between both players.
- Each player flips a Decimal Boss Card.
- Players compare their numbers. The player with the greater number takes both cards.
- The player with the most cards at the end of the round wins!

Relate Fractions and Decimals Chapter Practice 10
10.1 Understand Tenths
Write the fraction or mixed number as a decimal.
Question 1.
\(\frac{8}{10}\)
Answer: The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Explanation:
The given fraction is: \(\frac{8}{10}\)
Now,
The representation of \(\frac{8}{10}\) in the place-value chart is:

In \(\frac{8}{10}\),
8 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{8}{10}\) in the decimal form is: 0.8
Question 2.
\(\frac{3}{10}\)
Answer: The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Explanation:
The given fraction is: \(\frac{3}{10}\)
Now,
The representation of \(\frac{3}{10}\) in the place-value chart is:

In \(\frac{3}{10}\),
3 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Question 3.
6\(\frac{7}{10}\)
Answer: The representation of 6\(\frac{7}{10}\) in the decimal form is: 6.7
Explanation:
The given fraction is: 6\(\frac{7}{10}\)
Now,
The representation of 6\(\frac{7}{10}\) in the place-value chart is:

In 6\(\frac{7}{10}\),
6 represents the one’s position
7 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 6\(\frac{7}{10}\) in the decimal form is: 6.7
Question 4.
15\(\frac{4}{10}\)
Answer: The representation of 15\(\frac{4}{10}\) in the decimal form is: 15.4
Explanation:
The given fraction is: 15\(\frac{4}{10}\)
Now,
The representation of 15\(\frac{4}{10}\) in the place-value chart is:

In 15\(\frac{4}{10}\),
1 represents the ten’s position
5 represents the one’s position
4 represents the tenth’s position
The formula for converting fraction to a decimal is Decimal = Numerator ÷ Denominator
Hence,
The representation of 15\(\frac{4}{10}\) in the decimal form is: 15.4
Write the number as a fraction or mixed number and as a decimal.
Question 5.
two tenths
Answer:
The representation of two-tenths in the fraction form is: \(\frac{2}{10}\)
The representation of two-tenths in the decimal form is: 0.2
Explanation:
The given word form is: Two-tenths
So,
The representation of two-tenths in the fraction form is: \(\frac{2}{10}\)
Now,
The representation of \(\frac{2}{10}\) in the place-value chart is:

In \(\frac{2}{10}\),
2 represents the tenth’s position
Hence,
The representation of \(\frac{2}{10}\) in the decimal form is: 0.2
Question 6.
thirteen and six tenths
Answer:
The representation of thirteen and six-tenths in the fraction form is: 13\(\frac{6}{10}\)
The representation of thirteen and six-tenths in the decimal form is: 13.6
Explanation:
The given word form is: Thirteen and six-tenths
So,
The representation of thirteen and six-tenths in the fraction form is: 13\(\frac{6}{10}\)
Now,
The representation of 13\(\frac{6}{10}\) in the place-value chart is:

In 13\(\frac{6}{10}\),
1 represents the ten’s position
3 represents the one’s position
6 represents the tenth’s position
Hence,
The representation of 13\(\frac{6}{10}\) in the decimal form is: 13.6
Question 7.
Modeling Real Life
You bake 2 loaves of banana bread for a party. You cut each loaf into10 equal pieces. The guests eat 18 pieces. Write the fraction and decimal that represent how many loaves the guests eat in all.

Answer:
The representation of the loaves that the guests eat in the fraction form is: \(\frac{18}{20}\)
The representation of the loaves that the guests eat in the decimal form is: 0.9
Explanation:
It is given that you bake 2 loaves of banana bread and you cut each banana bread into 10 pieces
So,
The total number of pieces is: 20 pieces
It is also given that the guests eat 18 pieces.
So,
The number of pieces eaten by guests is: 18
So,
The representation of the loaves that the guests eat in the fraction form is: \(\frac{18}{20}\)
The representation of the loaves that the guests eat in the decimal form is: 0.9
10.2 Understand Hundredths
Write the fraction or mixed number as a decimal.
Question 8.
\(\frac{10}{100}\)
Answer: The representation of \(\frac{10}{100}\) in the form of decimal number is: 0.10
Explanation:
The given fraction is: \(\frac{10}{100}\)
Now,
The representation of \(\frac{10}{100}\) in the place-value chart is:
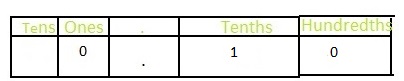
In \(\frac{10}{100}\),
0 represents the hundredth position
1 represents the tenth position
Hence,
The representation of \(\frac{10}{100}\) in the decimal form is: 0.10
Question 9.
\(\frac{6}{100}\)
Answer: The representation of \(\frac{6}{100}\) in the form of decimal number is: 0.06
Explanation:
The given fraction is: \(\frac{6}{100}\)
Now,
The representation of \(\frac{6}{100}\) in the place-value chart is:

In \(\frac{6}{100}\),
6 represents the hundredth position
0 represents the tenth position
Hence,
The representation of \(\frac{6}{100}\) in the decimal form is: 0.06
Question 10.
8\(\frac{75}{100}\)
Answer: The representation of 8\(\frac{75}{100}\) in the form of a decimal number is: 8.75
Explanation:
The given fraction is: 8\(\frac{75}{100}\)
Now,
The representation of 8\(\frac{75}{100}\) in the place-value chart is:
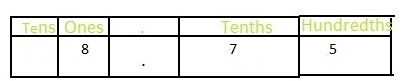
In 8\(\frac{75}{100}\),
8 represents the one’s position
5 represents the hundredth position
7 represents the tenth position
Hence,
The representation of 8\(\frac{75}{100}\) in the decimal form is: 8.75
Question 11.
34\(\frac{2}{100}\)
Answer: The representation of 34\(\frac{2}{100}\) in the form of a decimal number is: 34.02
Explanation:
The given fraction is: 34\(\frac{2}{100}\)
Now,
The representation of 34\(\frac{2}{100}\) in the place-value chart is:

In 8\(\frac{75}{100}\),
3 represents the ten’s position
4 represents the one’s position
2 represents the hundredth position
0 represents the tenth position
Hence,
The representation of 34\(\frac{2}{100}\) in the decimal form is: 34.02
Write the number as a fraction or mixed number and as a decimal.
Question 12.
thirty-seven hundredths
Answer:
The representation of thirty-seven hundredths in the fraction form is: \(\frac{37}{100}\)
The representation of thirty-seven hundredths in the decimal form is: 0.37
Explanation:
The given word form is: Thirty-seven hundredths
So,
The representation of thirty-seven hundredths in the fraction form is: \(\frac{37}{100}\)
Now,
The representation of \(\frac{37}{100}\) in the place-value chart is:
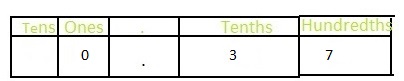
In \(\frac{37}{100}\),
7 represents the hundredth’s position
3 represents the tenth’s position
Hence,
The representation of \(\frac{37}{100}\) in the decimal form is: 0.37
Question 13.
nineteen and forty-one hundredths
Answer:
The representation of nineteen and forty-seven hundredths in the fraction form is: 19\(\frac{47}{100}\)
The representation of nineteen and forty-seven hundredths in the decimal form is: 19.47
Explanation:
The given word form is: Nineteen and forty-seven hundredths
So,
The representation of nineteen and forty-seven hundredths in the fraction form is: 19\(\frac{47}{100}\)
Now,
The representation of 19\(\frac{47}{100}\) in the place-value chart is:
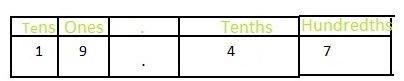
In 19\(\frac{47}{100}\),
1 represents the ten’s position
9 represents the one’s position
7 represents the hundredth’s position
4 represents the tenth’s position
Hence,
The representation of 19\(\frac{47}{100}\) in the decimal form is: 19.47
10.3 Fractions and Decimals
Write the number as tenths in fraction form and decimal form.
Question 14.
\(\frac{30}{100}\)
Answer:
The representation of \(\frac{30}{100}\) as tenths in the fraction form is: \(\frac{3}{10}\)
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Explanation:
The given fraction is: \(\frac{30}{100}\)
So, to write \(\frac{30}{100}\) as tenths, divide the fraction and numerator of \(\frac{30}{100}\) with 10.
So,
Firstly the numerators 30 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{30}{100}=\frac{30 \div 10}{100 \div 10}=\frac{8}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{30}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{30}{100}\) as tenths in the fraction form is: \(\frac{3}{10}\)
The representation of \(\frac{3}{10}\) in the decimal form is: 0.3
Question 15.
\(\frac{90}{100}\)
Answer:
The representation of \(\frac{90}{100}\) as tenths in the fraction form is: \(\frac{39{10}\)
The representation of \(\frac{39}{10}\) in the decimal form is: 0.9
Explanation:
The given fraction is: \(\frac{90}{100}\)
So, to write \(\frac{390}{100}\) as tenths, divide the fraction and numerator of \(\frac{90}{100}\) with 10.
So,
Firstly the numerators 90 and 10 are divided and then the denominators 100 and 10 are divided
So,
\(\frac{90}{100}=\frac{90 \div 10}{100 \div 10}=\frac{8}{10}\)
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{90}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{90}{100}\) as tenths in the fraction form is: \(\frac{9}{10}\)
The representation of \(\frac{9}{10}\) in the decimal form is: 0.9
Question 16.
0.50
Answer:
The representation of 0.50 as tenths in the fraction form is: \(\frac{5}{10}\)
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Explanation:
The given decimal number is: 0.50
So,
The representation of 0.50 in the fraction form is: \(\frac{50}{100}\)
So, to write \(\frac{50}{100}\) as tenths,divide the fraction and numerator of \(\frac{50}{100}\) with 10.
So,
Firstly the numerators 50 and 10 are divided and then the denominators 100 and 10 are divided
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{5}{10}\) in the place-value chart is:
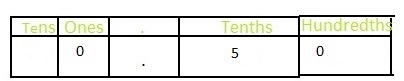
Hence,
The representation of \(\frac{50}{100}\) as tenths in the fraction form is: \(\frac{5}{10}\)
The representation of \(\frac{5}{10}\) in the decimal form is: 0.5
Write the number as hundredths in fraction form and decimal form.
Question 17.
\(\frac{7}{10}\)
Answer:
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
Explanation:
The given fraction is: \(\frac{7}{10}\)
So, to write \(\frac{7}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{7}{10}\) with 10.
So,
Firstly the numerators 7 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{70}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{7}{10}\) as hundredths in the fraction form is: \(\frac{70}{100}\)
The representation of \(\frac{70}{100}\) in the decimal form is: 0.70
Question 18.
\(\frac{4}{10}\)
Answer:
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
The representation of \(\frac{40}{100}\) in the decimal form is: 0.40
Explanation:
The given fraction is: \(\frac{4}{10}\)
So, to write \(\frac{4}{10}\) as hundredths, multiply the fraction and numerator of \(\frac{4}{10}\) with 10.
So,
Firstly the numerators 4 and 10 are multiplied and then the denominators 10 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{40}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
The representation of \(\frac{40}{100}\) in the decimal form is: 0.40
Question 19.
0.6
Answer:
The representation of 0.6 as hundredths in the fraction form is: \(\frac{60}{100}\)
The representation of \(\frac{60}{100}\) in the decimal form is: 0.60
Explanation:
The given decimal number is: 0.6
So,
The representation of 0.6 in the fraction form is: \(\frac{6}{10}\)
So, to write \(\frac{6}{10}\) as hundredths,multiply the fraction and numerator of \(\frac{6}{10}\) with 10.
So,
Firstly the numerators 6 and 10 are multiplied and then the denominators 100 and 10 are multiplied
We know that,
Decimal = Numerator ÷ Denominator
So,
The representation of \(\frac{60}{100}\) in the place-value chart is:

Hence,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
The representation of \(\frac{60}{100}\) in the decimal form is: 0.60
10.4 Compare Decimals
Compare
Question 20.
![]()
Answer: 0.79 is greater than 0.72
Explanation:
The given decimal numbers are: 0.79 and 0.72
The representation of 0.79 and 0.72 in the place-value chart is:
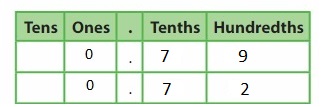
So,
From the above place-value chart,
we can observe that one’s and tenth’s positions are the same.
So,
Compare the hundredth’s position 9 and 2
So, 9 hundredths > 2 hundredths
Hence, from the above,
We can conclude that 0.79 is greater than 0.72
Question 21.
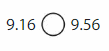
Answer: 9.16 is less than 9.56
Explanation:
The given decimal numbers are: 9.16 and 9.56
The representation of 9.16 and 9.56 in the place-value chart is:
So,
From the above place-value chart,
we can observe that one’s and hundredth’s positions are the same.
So,
Compare the tenth’s position 1 and 5
So, 1 hundredths < 5 hundredths
Hence, from the above,
We can conclude that 9.16 is less than 9.56
Question 22.
![]()
Answer: 11.40 is equal to 11.4
Explanation:
The given decimal numbers are: 11.40 and 11.4
The representation of 11.40 and 11.4 in the place-value chart is:
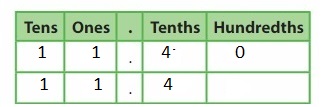
So,
From the above place-value chart,
we can observe that one’s, tenth’s, and hundredth’s positions are the same.
So,
Compare the tenth’s position 4 and 4
So, 4 hundredths = 4 hundredths
Hence, from the above,
We can conclude that 11.40 is equal to 11.4
Open-Ended
Complete the statement to make it true.
Question 23.
![]()
Answer: 0.19 is greater than 0.15
Explanation:
Let the missing number be 1
So,
The given decimal numbers are: 0.19 and 0.15
The representation of 0.19 and 0.15 in the place-value chart is:
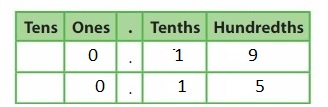
So,
From the above place-value chart,
we can observe that one’s and tenth’s positions are the same.
So,
Compare the hundredth’s position 9 and 5
So, 9 hundredths > 5 hundredths
Hence, from the above,
We can conclude that 0.19 is less than 0.15
Question 24.
![]()
Answer: 6.30 is equal to 6.3
Explanation:
Let the missing number be 0
So,
The given decimal numbers are: 6.30 and 6.3
The representation of 6.30 and 6.3 in the place-value chart is:
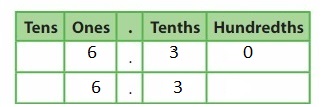
So,
From the above place-value chart,
we can observe that one’s, hundredth’s, and tenth’s positions are the same.
So,
Compare the hundredth’s position 0 and 0
So, 0 hundredths = 0 hundredths
Hence, from the above,
We can conclude that 6.30 is equal to 6.3
Question 25.
___ > 40.48
Answer: 40.58 is greater than 40.48
Explanation:
Let the missing number be 40.58
So,
The given decimal numbers are: 40.58 and 40.48
The representation of 40.58 and 40.48 in the place-value chart is:
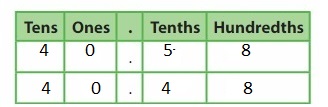
So,
From the above place-value chart,
we can observe that one’s and hundredth’s positions are the same.
So,
Compare the tenth’s position 9 and 5
So, 5 tenths > 4 tenths
Hence, from the above,
We can conclude that 40.58 is greater than 40.48
Question 26.
Open-Ended
What might Newton’s number be?

Answer: Newton’s number might be: 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29
Explanation:
It is given that Newton’s number will be between 0.2 and 0.3
So,
Newton’s number might be: 0.21, 0.22, 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29
It is also given that the highest digit will be in the hundredth’s place
Hence,
Newton’s number might be: 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29
10.5 Add Decimal Fractions and Decimals
Find the sum.
Question 27.
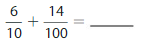
Answer:
The representation of the sum in the fraction form is:
\(\frac{6}{10}\) + \(\frac{14}{100}\) = \(\frac{74}{100}\)
The representation of \(\frac{74}{100}\) in the decimal for is: 0.74
Explanation:
The given fractions are: \(\frac{14}{100}\) and \(\frac{6}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{6}{10}\) as the hundredths, we have to multiply \(\frac{6}{10}\) by 10
So,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
So,
\(\frac{60}{100}\) + \(\frac{14}{100}\)
= \(\frac{60 + 14}{100}\)
= \(\frac{74}{100}\)
The representation of \(\frac{74}{100}\) in the decimal form is: 0.74
Hence from the above,
We can conclude that
\(\frac{6}{10}\) + \(\frac{14}{100}\) = \(\frac{74}{100}\)
The representation of \(\frac{74}{100}\) in the decimal for is: 0.74
Question 28.
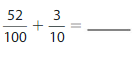
Answer:
The representation of the sum in the fraction form is:
\(\frac{3}{10}\) + \(\frac{52}{100}\) = \(\frac{82}{100}\)
The representation of \(\frac{82}{100}\) in the decimal for is: 0.82
Explanation:
The given fractions are: \(\frac{52}{100}\) and \(\frac{3}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{3}{10}\) as the hundredths, we have to multiply \(\frac{3}{10}\) by 10
So,
The representation of \(\frac{3}{10}\) as hundredths in the fraction form is: \(\frac{30}{100}\)
So,
\(\frac{30}{100}\) + \(\frac{52}{100}\)
= \(\frac{30 + 52}{100}\)
= \(\frac{82}{100}\)
The representation of \(\frac{82}{100}\) in the decimal form is: 0.82
Hence from the above,
We can conclude that
\(\frac{3}{10}\) + \(\frac{52}{100}\) = \(\frac{82}{100}\)
The representation of \(\frac{82}{100}\) in the decimal for is: 0.82
Question 29.
0.12 + 0.6 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{6}{10}\) + \(\frac{12}{100}\) = \(\frac{72}{100}\)
The representation of 012 + 0.6 in the decimal form is: 0.72
Explanation:
The given decimal numbers are: 0.6 and 0.12
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{12}{100}\) and \(\frac{6}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{6}{10}\) as the hundredths, we have to multiply \(\frac{6}{10}\) by 10
So,
The representation of \(\frac{6}{10}\) as hundredths in the fraction form is: \(\frac{60}{100}\)
So,
\(\frac{60}{100}\) + \(\frac{12}{100}\)
= \(\frac{60 + 12}{100}\)
= \(\frac{72}{100}\)
The representation of \(\frac{72}{100}\) in the decimal form is: 0.72
Hence from the above,
We can conclude that
\(\frac{6}{10}\) + \(\frac{12}{100}\) = \(\frac{72}{100}\)
The representation of \(\frac{72}{100}\) in the decimal for is: 0.72
Question 30.
0.4 + 0.72 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{4}{10}\) + \(\frac{72}{100}\) = \(\frac{112}{100}\)
The representation of 0.4 + 0.72 in the decimal form is: 1.12
Explanation:
The given decimal numbers are: 0.4 and 0.72
So, convert the two decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{72}{100}\) and \(\frac{4}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{4}{10}\) as the hundredths, we have to multiply \(\frac{4}{10}\) by 10
So,
The representation of \(\frac{4}{10}\) as hundredths in the fraction form is: \(\frac{40}{100}\)
So,
\(\frac{40}{100}\) + \(\frac{72}{100}\)
= \(\frac{72 + 40}{100}\)
= \(\frac{112}{100}\)
The representation of \(\frac{112}{100}\) in the decimal form is: 1.12
Hence from the above,
We can conclude that
\(\frac{4}{10}\) + \(\frac{72}{100}\) = \(\frac{112}{100}\)
The representation of \(\frac{112}{100}\) in the decimal for is: 1.12
Question 31.
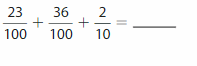
Answer:
The representation of the sum in the fraction form is:
\(\frac{23}{100}\) + \(\frac{36}{100}\) + \(\frac{2}{10}\) = \(\frac{79}{100}\)
The representation of \(\frac{79}{100}\) in the decimal for is: 0.79
Explanation:
The given fractions are: \(\frac{23}{100}\), \(\frac{36}{100}\) and \(\frac{2}{10}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{2}{10}\) as the hundredths, we have to multiply \(\frac{2}{10}\) by 10
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
So,
\(\frac{23}{100}\) + \(\frac{36}{100}\) + \(\frac{20}{100}\)
= \(\frac{23 + 36 + 20}{100}\)
= \(\frac{79}{100}\)
The representation of \(\frac{79}{100}\) in the decimal form is: 0.79
Hence from the above,
We can conclude that
\(\frac{2}{10}\) + \(\frac{23}{100}\) + \(\frac{36}{100}\) = \(\frac{79}{100}\)
The representation of \(\frac{79}{100}\) in the decimal for is: 0.79
Question 32.
0.18 + 0.2 + 0.07 = ___
Answer:
The representation of the sum in the fraction form is:
\(\frac{2}{10}\) + \(\frac{18}{100}\) + \(\frac{7}{100}\) = \(\frac{45}{100}\)
The representation of 0.18 + 0.2 + 0.07 in the decimal for is: 0.45
Explanation:
The given decimal numbers are: 0.18, 0.2 and 0.07
So, convert the three decimal numbers in to respective fractions.
So,
The given fractions are: \(\frac{18}{100}\) , \(\frac{2}{10}\) and \(\frac{7}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{2}{10}\) as the hundredths, we have to multiply \(\frac{2}{10}\) by 10
So,
The representation of \(\frac{2}{10}\) as hundredths in the fraction form is: \(\frac{20}{100}\)
So,
\(\frac{20}{100}\) + \(\frac{18}{100}\) + \(\frac{7}{100}\)
= \(\frac{20 + 18 + 7}{100}\)
= \(\frac{45}{100}\)
The representation of \(\frac{45}{100}\) in the decimal form is: 0.45
Hence from the above,
We can conclude that
\(\frac{2}{10}\) + \(\frac{18}{100}\) + \(\frac{7}{100}\) = \(\frac{45}{100}\)
The representation of \(\frac{45}{100}\) in the decimal for is: 0.45
Number Sense
Find the sum.
Question 33.
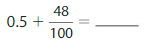
Answer:
The representation of the sum in the fraction form is:
\(\frac{5}{10}\) + \(\frac{48}{100}\) = \(\frac{98}{100}\)
The representation of 0.5 + \(\frac{48}{100}\) in the decimal for is: 0.98
Explanation:
The given numbers are: 0.5 and \(\frac{48}{100}\)
So, convert the decimal number in to respective fractions.
So,
The given fractions are: \(\frac{5}{10}\) and \(\frac{48}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{5}{10}\) as the hundredths, we have to multiply \(\frac{5}{10}\) by 10
So,
The representation of \(\frac{5}{10}\) as hundredths in the fraction form is: \(\frac{50}{100}\)
So,
\(\frac{50}{100}\) + \(\frac{48}{100}\)
= \(\frac{50 + 48}{100}\)
= \(\frac{98}{100}\)
The representation of \(\frac{98}{100}\) in the decimal form is: 0.98
Hence from the above,
We can conclude that
\(\frac{5}{10}\) + \(\frac{48}{100}\) = \(\frac{98}{100}\)
The representation of \(\frac{98}{100}\) in the decimal for is: 0.98
Question 34.
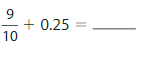
Answer:
The representation of the sum in the fraction form is:
\(\frac{9}{10}\) + \(\frac{25}{100}\) = \(\frac{115}{100}\)
The representation of 0.25 + \(\frac{9}{10}\) in the decimal for is: 1.15
Explanation:
The given numbers are: 0.25 and \(\frac{9}{10}\)
So, convert the decimal number in to respective fractions.
So,
The given fractions are: \(\frac{9}{10}\) and \(\frac{25}{100}\)
For addition, we have to make either denominators or the numerators equal.
so,
For making \(\frac{9}{10}\) as the hundredths, we have to multiply \(\frac{9}{10}\) by 10
So,
The representation of \(\frac{9}{10}\) as hundredths in the fraction form is: \(\frac{90}{100}\)
So,
\(\frac{90}{100}\) + \(\frac{25}{100}\)
= \(\frac{90 + 25}{100}\)
= \(\frac{115}{100}\)
The representation of \(\frac{115}{100}\) in the decimal form is: 1.15
Hence from the above,
We can conclude that
\(\frac{9}{10}\) + \(\frac{25}{100}\) = \(\frac{115}{100}\)
The representation of \(\frac{115}{100}\) in the decimal for is: 1.15
10.6 Fractions, Decimals, and Money
Find the total money amount. Then write the amount as a fraction or mixed number and as a decimal.
Question 35.
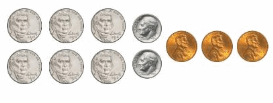
Answer: The total amount of money is: $1.13
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 penny = $0.01
The given money is: 3 pennies, 4 Quarters, and 2 nickels
So,
The total amount of money = ( 4 × 0.25 ) + ( 2 × 0.05 ) + ( 3 × 0.01 )
= 1 + 0.10 + 0.03
= 1.13
Hence,
The total amount of money is: $1.13
The representation of $1.13 in the fraction form is: 1\(\frac{13}{100}\) dollar
The representation of $1.13 in the decimal form is: 1.13
Question 36.

Answer: The total amount of money is: $2.11
Explanation:
We know that,
1 Quarter = $0.25
1 nickel = $0.05
1 penny = $0.01
The given money is: 1 penny, 4 Quarters, 1 dollar, and 2 nickels
So,
The total amount of money = ( 1 × 1 ) + ( 4 × 0.25 ) + ( 2 × 0.05 ) + ( 1 × 0.01 )
= 1 + 1 + 0.1 + 0.01
= 2.11
Hence,
The total amount of money is: $2.11
The representation of $2.11 in the fraction form is: 2\(\frac{11}{100}\) dollar
The representation if $2.11 in the decimal form is: 2.11
Question 37.
Write \(\frac{18}{100}\) as a money amount and as a decimal.
Answer: The representation of \(\frac{18}{100}\) as the total amount of money is: $0.18
Explanation:
The given fraction is: \(\frac{18}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.18
Question 38.
Write $0.94 as a fraction and as a decimal.
Answer: The representation of 0.94 as the total amount of money is: $0.94
Explanation:
The given decimal number is: 0.94
So,
The representation of 0.94 in the fraction form is: \(\frac{94}{100}\)
The given fraction will be given as an amount in dollars.
So,
The total amount of money in the decimal form is: $0.94
10.7 Operations with Money
Draw bills and coins to solve.
Question 39.
Bananas cost $0.29 per pound. You buy 3 pounds of bananas. How much money do you spend in all?
Answer: The total amount of money you spent is: $0.87
Explanation:
It is given that bananas cost $0.29 per pound and you bought 3 pounds of bananas
So,
The cost of bananas per pound is: $0.29
So,
The cost of 3 pounds of bananas = 3 × 0.29 = $0.87
hence, from the above,
We can conclude that the total amount of money you spent is: $0.89
Question 40.
Descartes has $3.50. He spends $1.75 on a journal. How much money does Descartes have left?
Answer: The amount of money Descartes left is: $1.75
Explanation:
It is given that Descartes has $3.50 and he spent $1.75 on a journal
So,
The total amount of money Descartes has: $3.50
The amount of money Descartes spent is: $1.75
So,
The amount of money Descartes left = The total amount of money Descartes has – The amount of money Descartes spent
= 3.50 – 1.75
= $1.75
Hence, from the above,
We can conclude that the amount of money Descartes left is: $1.75
Question 41.
You buy the items shown at a book fair. How much money do you spend in all?

Answer: The total amount of money you spent is: $7.49
Explanation:
The given figure is:

From the given figure,
The cost of a book is: $6.99
The cost of the pen is: $0.50
Hence,
The total amount of money you spent = The cost of a book + The cost of a pen
= 6.99 + 0.50
= $7.49
Hence, from the above,
We can conclude that the amount of money you spent is: $7.49
Conclusion:
All detailed and step by step explanations are covered in the Big Ideas Math Answers Grade 4 Chapter 10 Relate Fractions and Decimals. The solutions are prepared by the highly experienced subject experts after the ample research. This will help you to score the highest marks in the exams. Keep in touch with us to get the solution key of all Big Ideas Math Grade 4 Chapters.