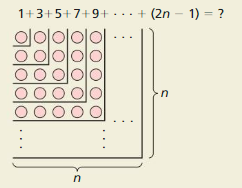
Big Ideas Math Algebra 2 Answer Key Chapter 8 Sequences and Series helps you to get a grip on the concepts from surface level to a deep level. Finish your homework or assignments in time by solving questions from B ig Ideas Math Book Algebra 2 Ch 8 Sequences and Series here. Access the user-friendly solutions provided for all the concepts of Chapter 8 Sequences and Series from Big Ideas Math Algebra 2 Textbooks here for free of cost.
Improve your performance in the final exams by practicing the Big Ideas Math Algebra 2 Answers Ch 8 Sequences and Series on a daily basis. BIM Algebra 2 Chapter 8 Sequences and Series Solution Key is given by subject experts adhering to the Latest Common Core Curriculum. Sequences and Series Big Ideas Math Algebra 2 Chapter 8 Answer Key encourages students and teachers to learn math in a simple and fun learning way.
Big Ideas Math Book Algebra 2 Answer Key Chapter 8 Sequences and Series
Check out Big Ideas Math Algebra 2 Answers Chapter 8 Sequences and Series aligned as per the Big Ideas Math Textbooks. Use the below available links for learning the Topics of BIM Algebra 2 Chapter 8 Sequences and Series easily and quickly. You just need to tap on them and avail the underlying concepts in it and score better grades in your exams. The Solutions covered here include Questions from Chapter Tests, Review Tests, Cumulative Practice, Cumulative Assessments, Exercise Questions, etc.
- Sequences and Series Maintaining Mathematical Proficiency – Page 407
- Sequences and Series Mathematical Practices – Page 408
- Lesson 8.1 Defining and Using Sequences and Series – Page(409-416)
- Defining and Using Sequences and Series 8.1 Exercises – Page(414-416)
- Lesson 8.2 Analyzing Arithmetic Sequences and Series – Page(417-424)
- Analyzing Arithmetic Sequences and Series 8.2 Exercises – Page(422-424)
- Lesson 8.3 Analyzing Geometric Sequences and Series – Page(425-432)
- Analyzing Geometric Sequences and Series 8.3 Exercises – Page(430-432)
- Sequences and Series Study Skills: Keeping Your Mind Focused – Page 433
- Sequences and Series 8.1 – 8.3 Quiz – Page 434
- Lesson 8.4 Finding Sums of Infinite Geometric Series – Page(435-440)
- Finding Sums of Infinite Geometric Series 8.4 Exercises – Page(439-440)
- Lesson 8.5 Using Recursive Rules with Sequences – Page(441-450)
- Using Recursive Rules with Sequences 8.5 Exercises – Page(447-450)
- Sequences and Series Performance Task: Integrated Circuits and Moore s Law – Page 451
- Sequences and Series Chapter Review – Page(452-454)
- Sequences and Series Chapter Test – Page 455
- Sequences and Series Cumulative Assessment – Page(456-457)
Sequences and Series Maintaining Mathematical Proficiency
Copy and complete the table to evaluate the function.
Question 1.
y = 3 − 2x
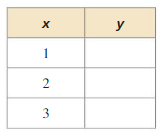
Answer:

Question 2.
y = 5x2 + 1
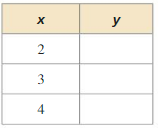
Answer:

Question 3.
y = −4x + 24
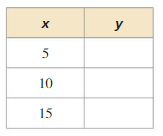
Answer:

Solve the equation. Check your solution(s).
Question 4.
7x + 3 = 31
Answer:
7x+3=31
7x=31-3
7x=28
x=28/7
x=4
Question 5.
\(\frac{1}{16}\) = 4 (\(\frac{1}{2}\)x
Answer:
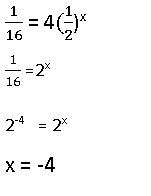
Question 6.
216 = 3(x + 6)
Answer:
216=3(x+6)
216=3x+18
3x=216-18
3x=198
x=198/3
x=66
Question 7.
2x + 16 = 144
Answer:
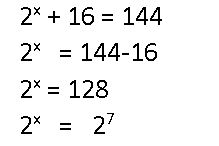
Question 8.
\(\frac{1}{4}\)x − 8 = 17
Answer:
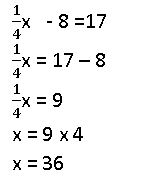
Question 9.
8(\(\frac{3}{4}\))x = \(\frac{27}{8}\)
Answer:
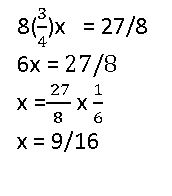
Question 10.
ABSTRACT REASONING
The graph of the exponential decay function f(x) = bx has an asymptote y = 0. How is the graph of f different from a scatter plot consisting of the points (1, b1), (2, b21 + b2), (3, b1 + b2 + b3), . . .? How is the graph of f similar?
Answer:
Sequences and Series Mathematical Practices
Mathematically proficient students consider the available tools when solving a mathematical problem.
Monitoring Progress
Use a spreadsheet to help you answer the question.
Question 1.
A pilot flies a plane at a speed of 500 miles per hour for 4 hours. Find the total distance flown at 30-minute intervals. Describe the pattern.
Answer:
Question 2.
A population of 60 rabbits increases by 25% each year for 8 years. Find the population at the end of each year. Describe the type of growth.
Answer:
Given,
A population of 60 rabbits increases by 25% each year for 8 years.
Year 1 of 8: 75
Year 2 of 8: 94
Year 3 of 8: 117
Year 4 of 8: 146
Year 5 of 8: 183
Year 6 of 8: 229
Year 7 of 8: 286
Year 8 of 8 (Final year): 357
Question 3.
An endangered population has 500 members. The population declines by 10% each decade for 80 years. Find the population at the end of each decade. Describe the type of decline.
Answer:
Question 4.
The top eight runners finishing a race receive cash prizes. First place receives $200, second place receives $175, third place receives $150, and so on. Find the fifth through eighth place prizes. Describe the type of decline.
Answer:
Lesson 8.1 Defining and Using Sequences and Series
Essential Question How can you write a rule for the nth term of a sequence?
A sequence is an ordered list of numbers. There can be a limited number or an infinite number of terms of a sequence.
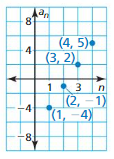
a1, a2, a3, a4, . . . , an, . . .Terms of a sequence
Here is an example. 1, 4, 7, 10, . . . , 3n-2, . . .
EXPLORATION 1
Writing Rules for Sequences

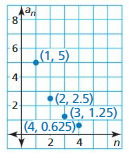
Work with a partner. Match each sequence with its graph. The horizontal axes represent n, the position of each term in the sequence. Then write a rule for the nth term of the sequence, and use the rule to find a10.
a. 1, 2.5, 4, 5.5, 7, . . .
b. 8, 6.5, 5, 3.5, 2, . . .
c. \(\frac{1}{4}, \frac{4}{4}, \frac{9}{4}, \frac{16}{4}, \frac{25}{4}, \ldots\)
d. \(\frac{25}{4}, \frac{16}{4}, \frac{9}{4}, \frac{4}{4}, \frac{1}{4}, \ldots\)
e. \(\frac{1}{2}\), 1, 2, 4, 8, . . .
f. 8, 4, 2, 1, \(\frac{1}{2}\), . . .
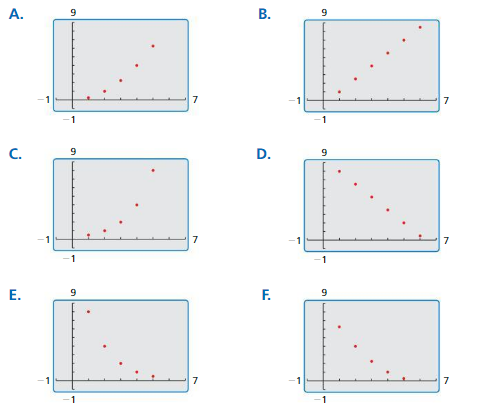
Communicate Your Answer
Question 2.
How can you write a rule for the nth term of a sequence?
Answer:
nth term of a sequence
an = a1 + (n-1)(d)
Question 3.
What do you notice about the relationship between the terms in (a) an arithmetic sequence and (b) a geometric sequence? Justify your
Answer:
An arithmetic sequence has a constant difference between each consecutive pair of terms. This is similar to the linear functions that have the form y=mx +b. A geometric sequence has a constant ratio between each pair of consecutive terms.
Monitoring Progress
Write the first six terms of the sequence.
Question 1.
an = n + 4
Answer
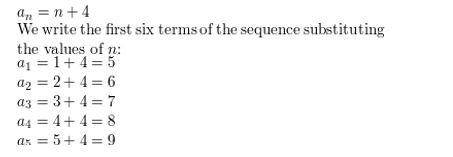
Question 2.
f(n) = (−2)n-1
Answer:
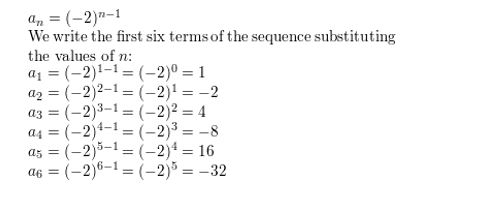
Question 3.
an = \(\frac{n}{n+1}\)
Answer:

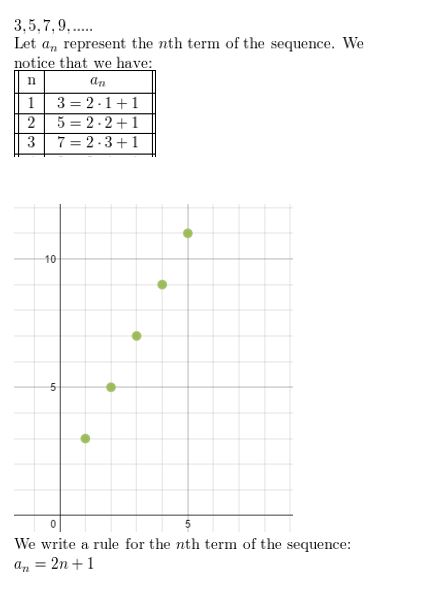
Describe the pattern, write the next term, graph the first five terms, and write a rule for the nth term of the sequence.
Question 4.
3, 5, 7, 9, . . .
Answer:
Question 5.
3, 8, 15, 24, . . .
Answer:

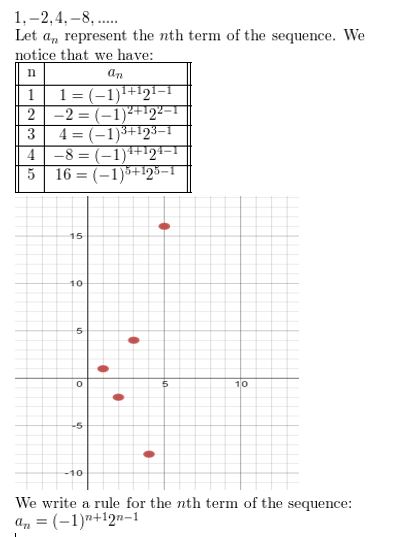
Question 6.
1, −2, 4, −8, . . .
Answer:
Question 7.
2, 5, 10, 17, . . .
Answer:
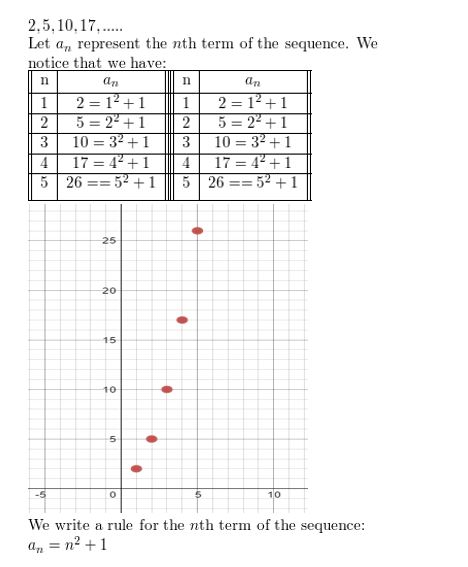
Question 8.
WHAT IF?
In Example 3, suppose there are nine layers of apples. How many apples are in the ninth layer?
Answer:

Write the series using summation notation.
Question 9.
5 + 10 + 15 +. . .+ 100
Answer:

Question 10.
\(\frac{1}{2}+\frac{4}{5}+\frac{9}{10}+\frac{16}{17}+\cdots\)
Answer:

Question 11.
6 + 36 + 216 + 1296 + . . .
Answer:

Question 12.
5 + 6 + 7 +. . .+ 12
Answer:

Find the sum.
Question 13.
\(\sum_{i=1}^{5}\) 8i
Answer:
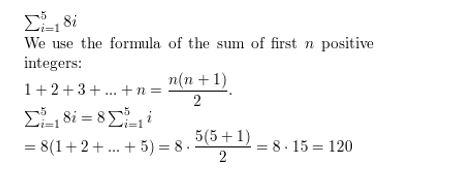
Question 14.
\(\sum_{k=3}^{7}\)(k2 − 1)
Answer:
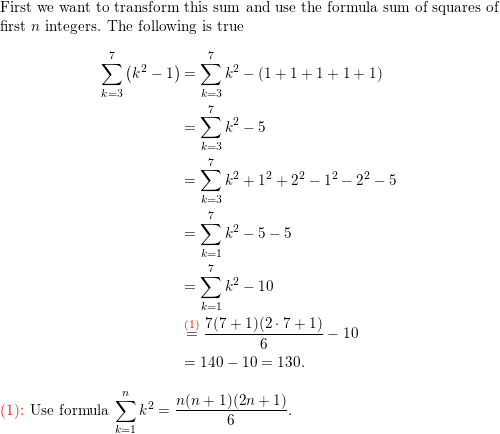
Question 15.
\(\sum_{i=1}^{34}\)1
Answer:
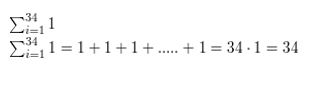
Question 16.
\(\sum_{k=1}^{6}\)k
Answer:

Question 17.
WHAT IF?
Suppose there are nine layers in the apple stack in Example 3. How many apples are in the stack?
Answer:
Defining and Using Sequences and Series 8.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is another name for summation notation?
Answer:
![]()
Question 2.
COMPLETE THE SENTENCE
In a sequence, the numbers are called __________ of the sequence.
Answer:
In a sequence, the numbers are called the terms of the sequence.
Question 3.
WRITING
Compare sequences and series.
Answer:

Question 4.
WHICH ONE DOESN’T BELONG?
Which does not belong with the other three? Explain your reasoning.
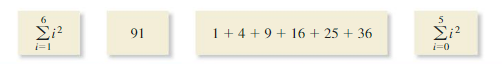
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 5–14, write the first six terms of the sequence.
Question 5.
an = n + 2
Answer:
Question 6.
an = 6 − n
Answer:
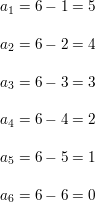
Question 7.
an = n2
Answer:
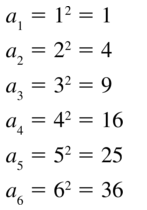
Question 8.
f(n) = n3 + 2
Answer:
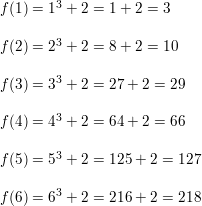
Question 9.
f(n) = 4n-1
Answer:
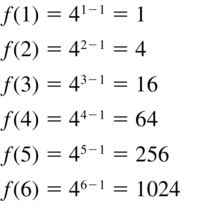
Question 10.
an = −n2
Answer:
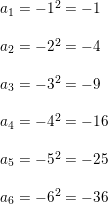
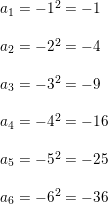
Question 11.
an = n2 − 5
Answer:
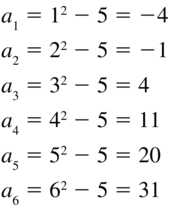
Question 12.
an = (n + 3)2
Answer:
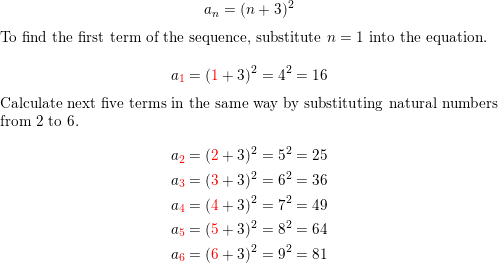
Question 13.
f(n) = \(\frac{2n}{n+2}\)
Answer:
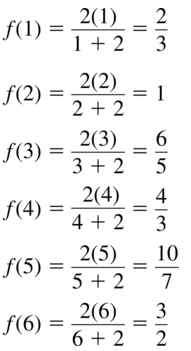
Question 14.
f(n) = \(\frac{n}{2n-1}\)
Answer:
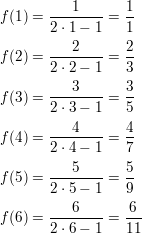
In Exercises 15–26, describe the pattern, write the next term, and write a rule for the nth term of the sequence.
Question 15.
1, 6, 11, 16, . . .
Answer:
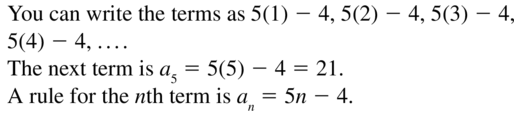
Question 16.
1, 2, 4, 8, . . .
Answer:

Question 17.
3.1, 3.8, 4.5, 5.2, . . .
Answer:

Question 18.
9, 16.8, 24.6, 32.4, . . .
Answer:

Question 19.
5.8, 4.2, 2.6, 1, −0.6 . . .
Answer:
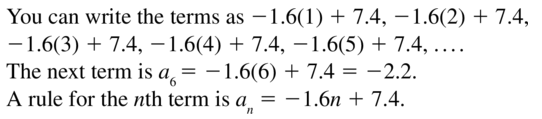
Question 20.
−4, 8, −12, 16, . . .
Answer:
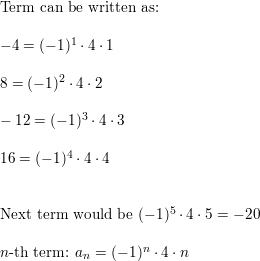
Question 21.
\(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \ldots\)
Answer:
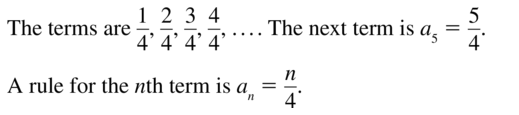
Question 22.
\(\frac{1}{10}, \frac{3}{20}, \frac{5}{30}, \frac{7}{40}, \ldots\)
Answer:
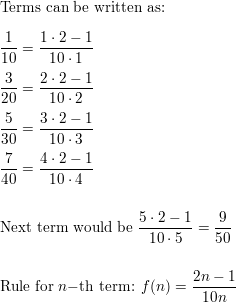
Question 23.
\(\frac{2}{3}, \frac{2}{6}, \frac{2}{9}, \frac{2}{12}, \ldots\)
Answer:
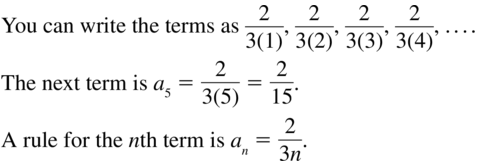
Question 24.
\(\frac{2}{3}, \frac{4}{4}, \frac{6}{5}, \frac{8}{6}, \ldots\)
Answer:
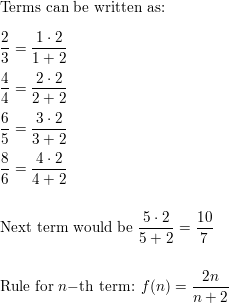
Question 25.
2, 9, 28, 65, . . .
Answer:
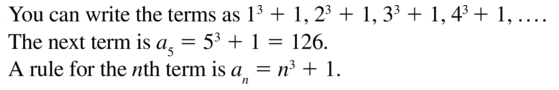
Question 26.
1.2, 4.2, 9.2, 16.2, . . .
Answer:

Question 27.
FINDING A PATTERN
Which rule gives the total number of squares in the nth figure of the pattern shown? Justify your answer.
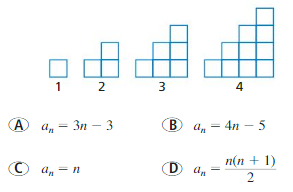
Answer:

Question 28.
FINDING A PATTERN
Which rule gives the total number of green squares in the nth figure of the pattern shown? Justify your answer.
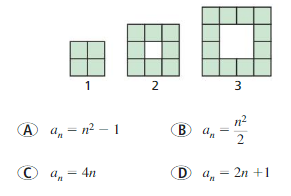
Answer:
A. an = n² – 1
a1 = 1 – 1 = 0
a2 = 2² – 1 = 4 – 1 = 3
a3 = 3² – 1 = 9 – 1 = 8
a4 = 4² – 1 = 16 – 1 = 15
B. an = n²/2
a1 = 1²/2 = 1/2
a2 = 2²/2 = 4/2 = 2
a3 = 3²/2 = 9/2
a4 = 4²/2 = 16/2 = 8
C. an = 4n
a1 = 4(1) = 4
a2 = 4(2) = 8
a3 = 4(3) = 12
a4 = 4(4) = 16
D. an = 2n + 1
a1 = 2(1) + 1 = 3
a2 = 2(2) + 1 = 5
a3 = 2(3) + 1 = 7
a4 = 2(4) + 1 = 9
Therefore C is the correct answer as the total number of green squares in the nth figure of the pattern shown in rule C.
Question 29.
MODELING WITH MATHEMATICS
Rectangular tables are placed together along their short edges, as shown in the diagram. Write a rule for the number of people that can be seated around n tables arranged in this manner. Then graph the sequence.

Answer:

Question 30.
MODELING WITH MATHEMATICS
An employee at a construction company earns $33,000 for the first year of employment. Employees at the company receive raises of $2400 each year. Write a rule for the salary of the employee each year. Then graph the sequence.
Answer:
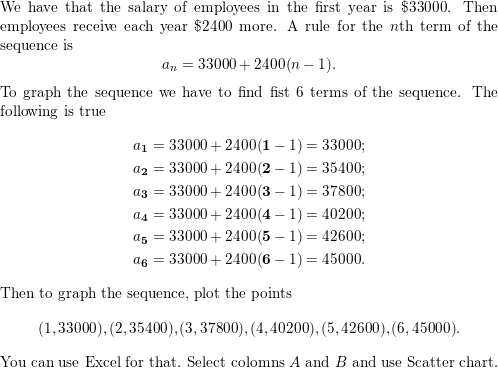
In Exercises 31–38, write the series using summation notation.
Question 31.
7 + 10 + 13 + 16 + 19
Answer:

Question 32.
5 + 11 + 17 + 23 + 29
Answer:
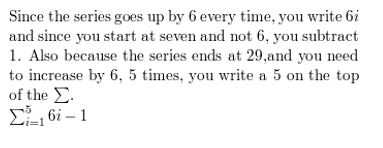
Question 33.
4 + 7 + 12 + 19 + . . .
Answer:

Question 34.
-1 + 2 + 7 + 14 + …..
Answer:

Question 35.
\(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\cdots\)
Answer:

Question 36.
\(\frac{1}{4}+\frac{2}{5}+\frac{3}{6}+\frac{4}{7}+\cdots\)
Answer:
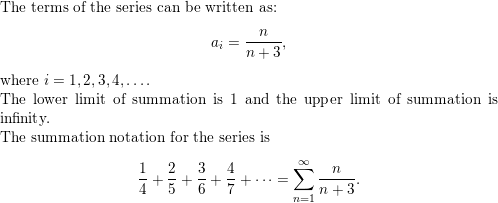
Question 37.
−3 + 4 − 5 + 6 − 7
Answer:
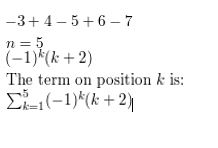
Question 38.
−2 + 4 − 8 + 16 − 32
Answer:

In Exercises 39–50, find the sum.
Question 39.
\(\sum_{i=1}^{6}\)2i
Answer:
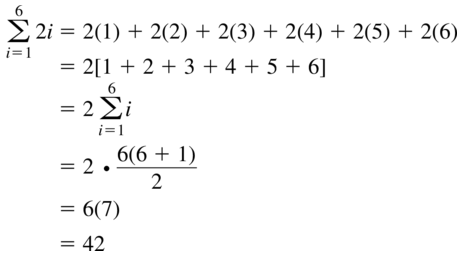
Question 40.
\(\sum_{i=1}^{5}\)7i
Answer:
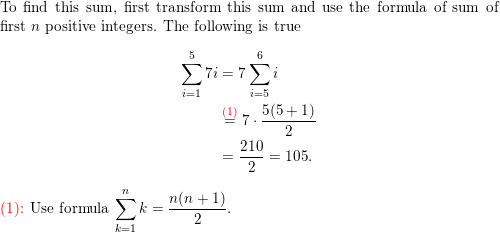
Question 41.
\(\sum_{n=0}^{4}\)n3
Answer:
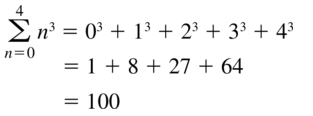
Question 42.
\(\sum_{k=1}^{4}\)3k2
Answer:
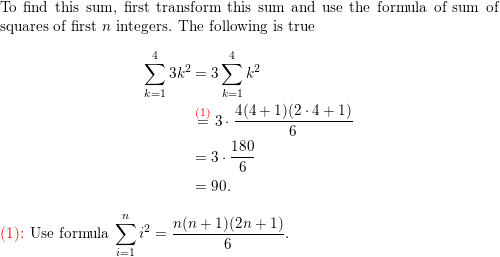
Question 43.
\(\sum_{k=3}^{6}\)(5k − 2)
Answer:
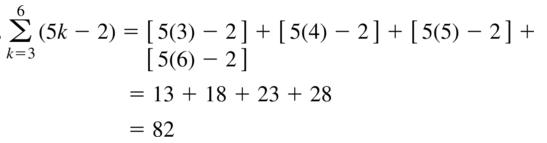
Question 44.
\(\sum_{n=1}^{5}\)(n2 − 1)
Answer:
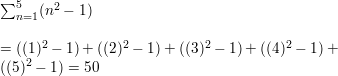
Question 45.
\(\sum_{i=2}^{8} \frac{2}{i}\)
Answer:
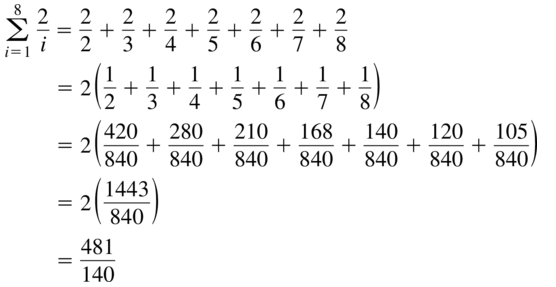
Question 46.
\(\sum_{k=4}^{6} \frac{k}{k+1}\)
Answer:
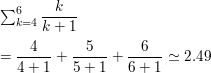
Question 47.
\(\sum_{i=1}^{35}\)1
Answer:
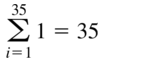
Question 48.
\(\sum_{n=1}^{16}\)n
Answer:
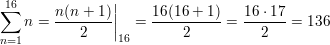
Question 49.
\(\sum_{i=10}^{25}\)i
Answer:
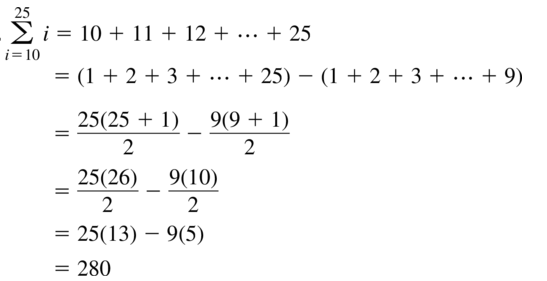
Question 50.
\(\sum_{n=1}^{18}\)n2
Answer:
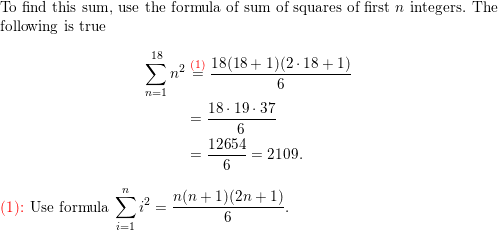
ERROR ANALYSIS In Exercises 51 and 52, describe and correct the error in finding the sum of the series.
Question 51.
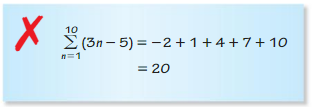
Answer:
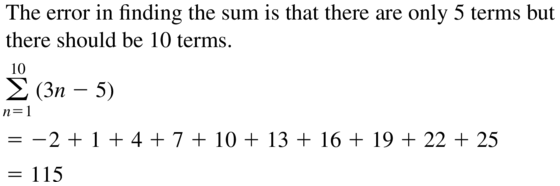
Question 52.
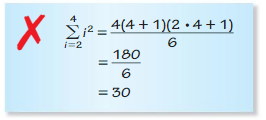
Answer:
Question 53.
PROBLEM SOLVING
You want to save $500 for a school trip. You begin by saving a penny on the first day. You save an additional penny each day after that. For example, you will save two pennies on the second day, three pennies on the third day, and so on.
a. How much money will you have saved after 100 days?
b. Use a series to determine how many days it takes you to save $500.
Answer:

Question 54.
MODELING WITH MATHEMATICS
You begin an exercise program. The first week you do 25 push-ups. Each week you do 10 more push-ups than the previous week. How many push-ups will you do in the ninth week? Justify your answer.

Answer:

Question 55.
MODELING WITH MATHEMATICS
For a display at a sports store, you are stacking soccer balls in a pyramid whose base is an equilateral triangle with five layers. Write a rule for the number of soccer balls in each layer. Then graph the sequence.

Answer:
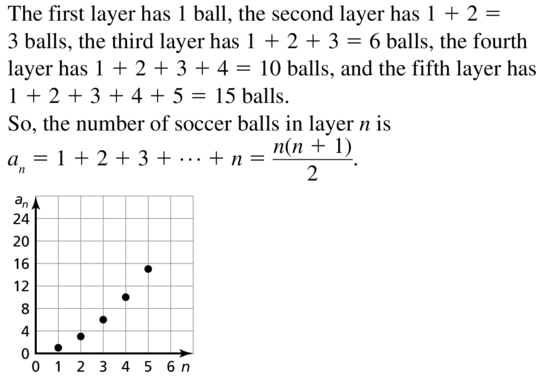
Question 56.
HOW DO YOU SEE IT?
Use the diagram to determine the sum of the series. Explain your reasoning.
Answer:
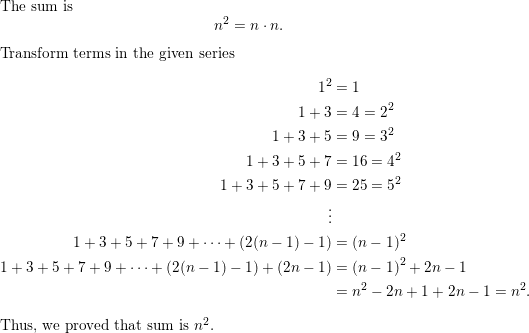
Question 57.
MAKING AN ARGUMENT
You use a calculator to evaluate \(\sum_{i=3}^{1659}\)i because the lower limit of summation is 3, not 1. Your friend claims there is a way to use the formula for the sum of the first n positive integers. Is your friend correct? Explain.
Answer:

Question 58.
MATHEMATICAL CONNECTIONS
A regular polygon has equal angle measures and equal side lengths. For a regular n-sided polygon (n ≥ 3), the measure an of an interior angle is given by an = \(\frac{180(n-2)}{n}\)
a. Write the first five terms of the sequence.
b. Write a rule for the sequence giving the sum Tn of the measures of the interior angles in each regular n-sided polygon.
c. Use your rule in part (b) to find the sum of the interior angle measures in the Guggenheim Museum skylight, which is a regular dodecagon.

Answer:
When n = 3
an = 180(n – 2)/n
an = 180(3 – 2)/3
an = 180/3 = 60
an = 60
when n = 4
an = 180(n – 2)/n
an = 180(4 – 2)/4
an = 180/3 = 60
an = 45 × 2
an = 90
The value of each of the interior angle of a 4-sided polygon is 90 degrees.
when n = 5
an = 180(n – 2)/n
an = 180(5 – 2)/5
an = 36 × 3
an = 108
The value of each of the interior angle of a 5-sided polygon is 108 degrees.
when n = 6
an = 180(n – 2)/n
an = 180(6 – 2)/6
an = 30 × 4
an = 120
The value of each of the interior angle of a 6-sided polygon is 120 degrees.
when n = 7
an = 180(n – 2)/n
an = 180(7 – 2)/7
an = 25.71 × 5
an = 128.55
The value of each of the interior angle of a 7-sided polygon is 128.55 degrees.
b. The rule for the sequence giving the sum Tn of the measures of the interior angles in each regular n-sided polygon is Tn = 180(n – 2).
c. Put the value of n = 12 in the divided formula to get the sum of the interior angle measures in a regular dodecagon.
Tn = 180(n – 2), n = 12
Tn = 180(12 – 2)
Tn = 180 × 10
Tn = 1800 degrees
Question 59.
USING STRUCTURE
Determine whether each statement is true. If so, provide a proof. If not, provide a counterexample.
Answer:


Question 60.
THOUGHT PROVOKING
In this section, you learned the following formulas.
\(\sum_{i=1}^{n}\)1 = n
\(\sum_{i=1}^{n}\)i = \(\frac{n(n+1)}{2}\)
\(\sum_{i=1}^{n}\)i2 = \(\frac{n(n+1)(2 n+1)}{6}\)
Write a formula for the sum of the cubes of the first n positive integers.
Answer:
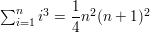
Question 61.
MODELING WITH MATHEMATICS
In the puzzle called the Tower of Hanoi, the object is to use a series of moves to take the rings from one peg and stack them in order on another peg. A move consists of moving exactly one ring, and no ring may be placed on top of a smaller ring. The minimum number an of moves required to move n rings is 1 for 1 ring, 3 for 2 rings, 7 for 3 rings, 15 for 4 rings, and 31 for 5 rings.
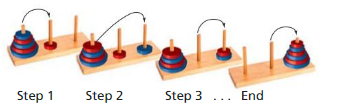
a. Write a rule for the sequence.
b. What is the minimum number of moves required to move 6 rings? 7 rings? 8 rings?
Answer:

Maintaining Mathematical Proficiency
Solve the system. Check your solution.
Question 62.
2x −y − 3z = 6
x + y + 4z =−1
3x − 2z = 8
Answer:
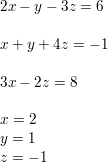
Question 63.
2x − 2y + z = 5
−2x + 3y + 2z = −1
x − 4y + 5z = 4
Answer:
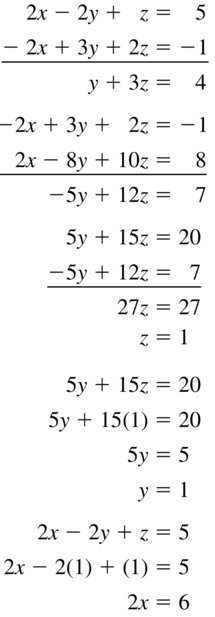
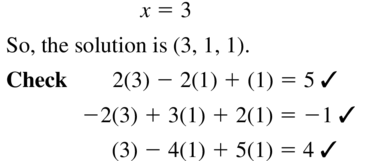
Question 64.
2x − 3y + z = 4
x − 2z = 1
y + z = 2
Answer:
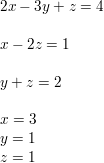
Lesson 8.2 Analyzing Arithmetic Sequences and Series
Essential Question How can you recognize an arithmetic sequence from its graph?
In an arithmetic sequence, the difference of consecutive terms, called the common difference, is constant. For example, in the arithmetic sequence 1, 4, 7, 10, . . . , the common difference is 3.
EXPLORATION 1
Recognizing Graphs of Arithmetic Sequences
Work with a partner. Determine whether each graph shows an arithmetic sequence. If it does, then write a rule for the nth term of the sequence, and use a spreadsheet to fond the sum of the first 20 terms. What do you notice about the graph of an arithmetic sequence?
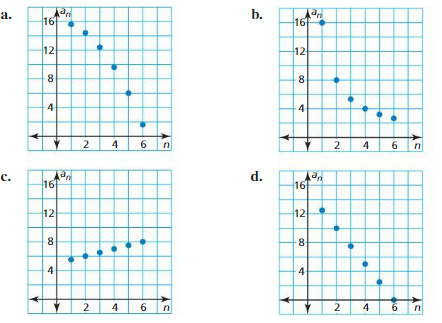
EXPLORATION 2
Finding the Sum of an Arithmetic Sequence
Work with a partner. A teacher of German mathematician Carl Friedrich Gauss (1777–1855) asked him to find the sum of all the whole numbers from 1 through 100. To the astonishment of his teacher, Gauss came up with the answer after only a few moments. Here is what Gauss did:
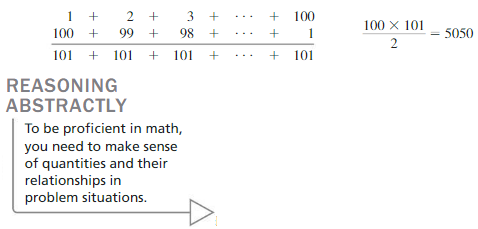
Explain Gauss’s thought process. Then write a formula for the sum Sn of the first n terms of an arithmetic sequence. Verify your formula by finding the sums of the first 20 terms of the arithmetic sequences in Exploration 1. Compare your answers to those you obtained using a spreadsheet.
Communicate Your Answer
Question 3.
How can you recognize an arithmetic sequence from its graph?
Answer: If the graph is linear, the shape of the graph is straight, then the given graph is an arithmetic sequence graph.
Question 4.
Find the sum of the terms of each arithmetic sequence.
a. 1, 4, 7, 10, . . . , 301
b. 1, 2, 3, 4, . . . , 1000
c. 2, 4, 6, 8, . . . , 800
Answer:
a. tn = a + (n – 1)d
301 = 4 + (n – 1)3
301 = 4 + 3n – 3
301 = 3n + 1
3n = 300
n = 300/3
n = 100
b. 1000 = 2 + (n – 1)1
1000 = 2 + n – 1
1000 = n + 1
n = 999
c. 800 = 4 + (n – 1)2
800 = 4 + 2n – 2
800 = 2 + 2n
798 = 2n
n = 399
Monitoring Progress
Tell whether the sequence is arithmetic. Explain your reasoning.
Question 1.
2, 5, 8, 11, 14, . . .
Answer:
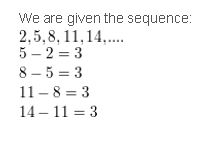
Question 2.
15, 9, 3, −3, −9, . . .
Answer:
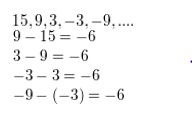
Question 3.
8, 4, 2, 1, \(\frac{1}{2}\), . . .
Answer:
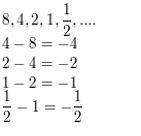
Question 4.
Write a rule for the nth term of the sequence 7, 11, 15, 19, . . .. Then find a15.
Answer:

Write a rule for the nth term of the sequence. Then graph the first six terms of the sequence.
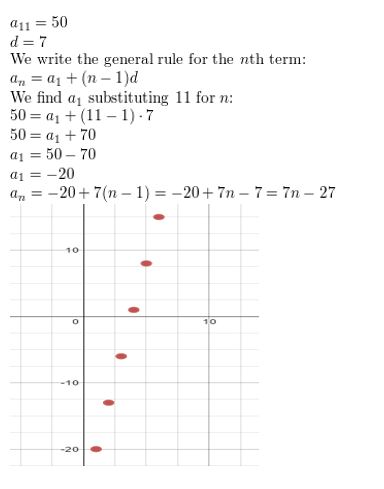
Question 5.
a11 = 50, d = 7
Answer:
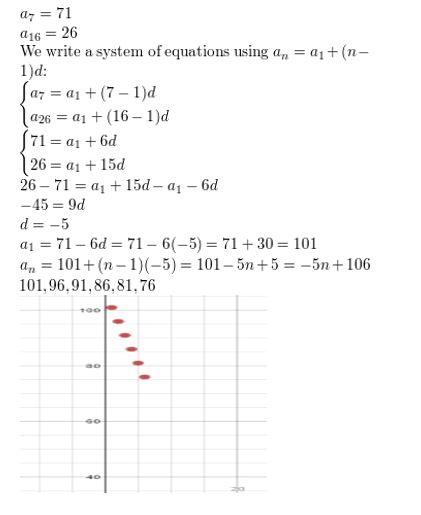
Question 6.
a7 = 71, a16 = 26
Answer:
Find the sum.
Question 7.
\(\sum_{i=1}^{10}\)9i
Answer:
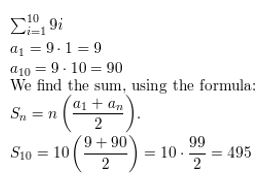
Question 8.
\(\sum_{k=1}^{12}\)(7k + 2)
Answer:
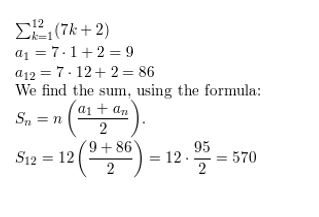
Question 9.
\(\sum_{n=1}^{20}\)(−4n + 6)
Answer:
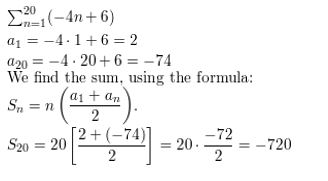
Question 10.
WHAT IF?
In Example 6, how many cards do you need to make a house of cards with eight rows?
Answer:

Analyzing Arithmetic Sequences and Series 8.2 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The constant difference between consecutive terms of an arithmetic sequence is called the _______________.
Answer:
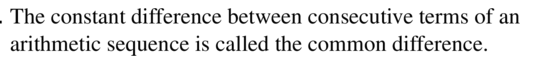
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, tell whether the sequence is arithmetic. Explain your reasoning.
Question 3.
1, −1, −3, −5, −7, . . .
Answer:
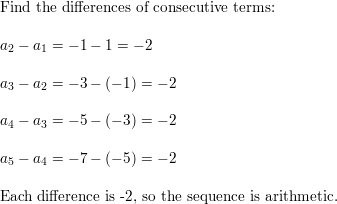
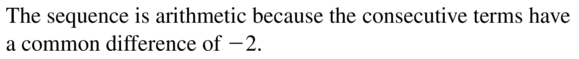
Question 4.
12, 6, 0, −6, −12, . . .
Answer:

Question 5.
5, 8, 13, 20, 29, . . .
Answer:
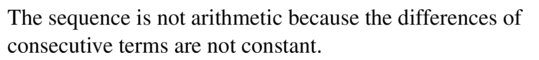
Question 6.
3, 5, 9, 15, 23, . . .
Answer:
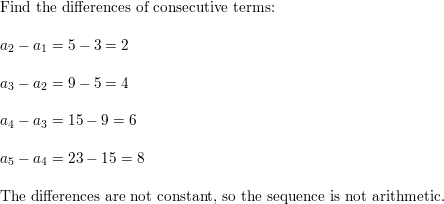
Question 7.
36, 18, 9, \(\frac{9}{2}\), \(\frac{9}{4}\), . . .
Answer:
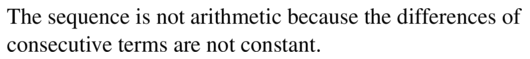
Question 8.
81, 27, 9, 3, 1, . . .
Answer:
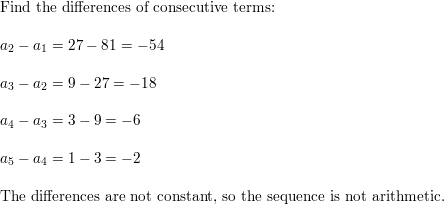
Question 9.
\(\frac{1}{2}, \frac{3}{4}, 1, \frac{5}{4}, \frac{3}{2}, \ldots\)
Answer:
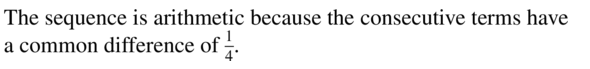
Question 10.
\(\frac{1}{6}, \frac{1}{2}, \frac{5}{6}, \frac{7}{6}, \frac{3}{2}, \ldots\)
Answer:

Question 11.
WRITING EQUATIONS
Write a rule for the arithmetic sequence with the given description.
a. The first term is −3 and each term is 6 less than the previous term.
b. The first term is 7 and each term is 5 more than the previous term.
Answer:

Question 12.
WRITING
Compare the terms of an arithmetic sequence when d > 0 to when d < 0.
Answer:
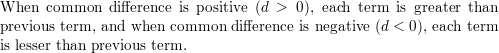
In Exercises 13–20, write a rule for the nth term of the sequence. Then find a20.
Question 13.
12, 20, 28, 36, . . .
Answer:

Question 14.
7, 12, 17, 22, . . .
Answer:
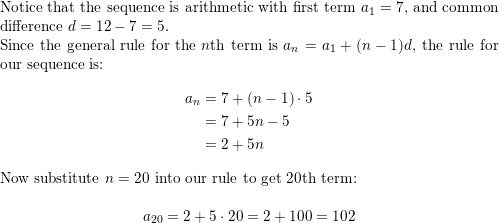
Question 15.
51, 48, 45, 42, . . .
Answer:

Question 16.
86, 79, 72, 65, . . .
Answer:
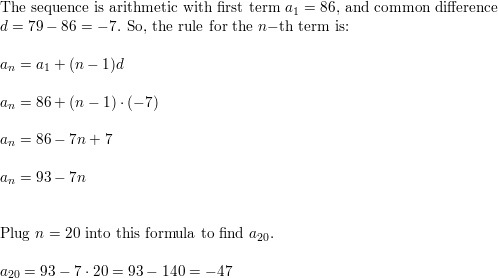
Question 17.
−1, −\(\frac{1}{3}\), \(\frac{1}{3}\), 1, . . .
Answer:

Question 18.
−2, −\(\frac{5}{4}\), −\(\frac{1}{2}\), \(\frac{1}{4}\), . . .
Answer:
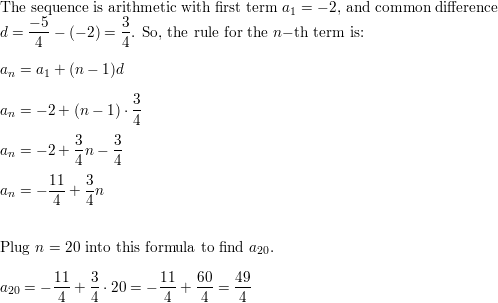
Question 19.
2.3, 1.5, 0.7, −0.1, . . .
Answer:

Question 20.
11.7, 10.8, 9.9, 9, . . .
Answer:
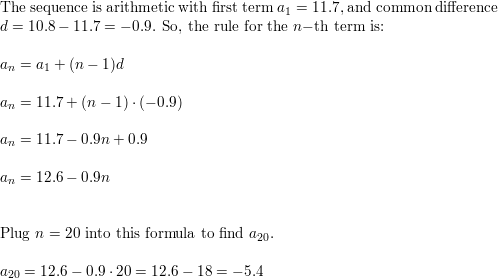
ERROR ANALYSIS In Exercises 21 and 22, describe and correct the error in writing a rule for the nth term of the arithmetic sequence 22, 9, -4, -17, -30, . . ..
Question 21.
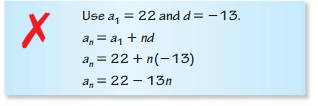
Answer:

Question 22.

Answer:

In Exercises 23–28, write a rule for the nth term of the sequence. Then graph the first six terms of the sequence.
Question 23.
a11 = 43, d = 5
Answer:
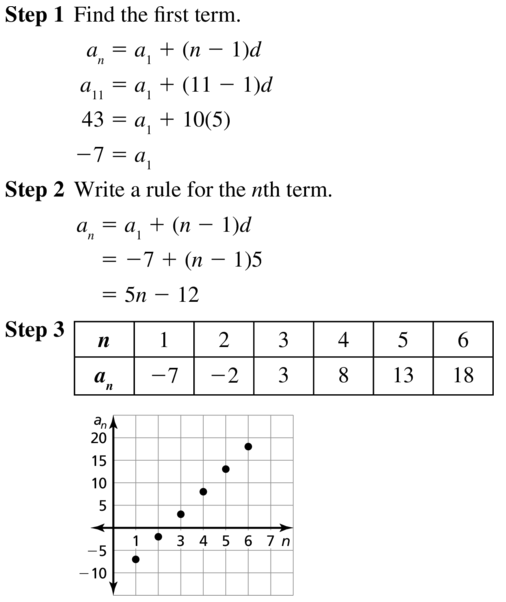
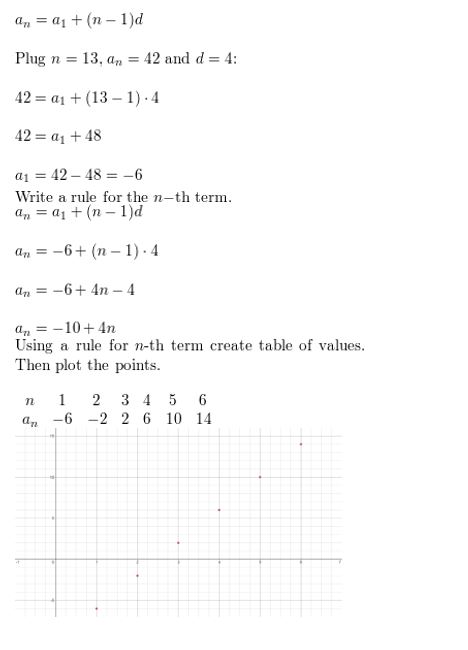
Question 24.
a13 = 42, d = 4
Answer:
Question 25.
a20 = −27, d =−2
Answer:

Question 26.
a15 = −35, d =−3
Answer:

Question 27.
a17 = −5, d = −\(\frac{1}{2}\)
Answer:
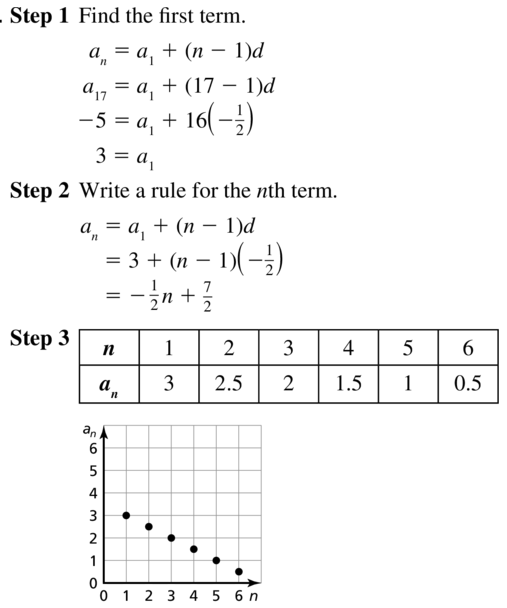
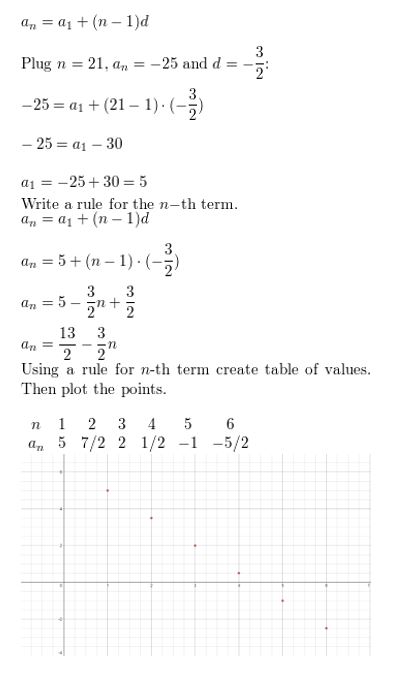
Question 28.
a21 = −25, d = −\(\frac{3}{2}\)
Answer:
Question 29.
USING EQUATIONS
One term of an arithmetic sequence is a8 = −13. The common difference is −8. What is a rule for the nth term of the sequence?
A. an = 51 + 8n
B. an = 35 + 8n
C. an = 51 − 8n
D. an = 35 − 8n
Answer:

Question 30.
FINDING A PATTERN
One term of an arithmetic sequence is a12 = 43. The common difference is 6. What is another term of the sequence?
A. a3 = −11
B. a4 = −53
C. a5 = 13
D. a6 = −47
Answer:

In Exercises 31–38, write a rule for the nth term of the arithmetic sequence.
Question 31.
a5 = 41, a10 = 96
Answer:

Question 32.
a7 = 58, a11 = 94
Answer:

Question 33.
a6 =−8, a15 = −62
Answer:

Question 34.
a8 = −15, a17 = −78
Answer:
Question 35.
a18 = −59, a21 = −71
Answer:

Question 36.
a12 = −38, a19 = −73
Answer: 12 + 38 + 19 + 73 = 142
Question 37.
a8 = 12, a16 = 22
Answer:

Question 38.
a12 = 9, a27 = 15
Answer:
WRITING EQUATIONS In Exercises 39–44, write a rule for the sequence with the given terms.
Question 39.
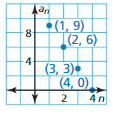
Answer:
Question 40.
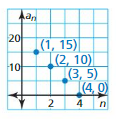
Answer:
Question 41.
Answer:
Question 42.
Answer:

Question 43.
Answer:
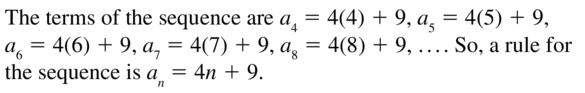
Question 44.
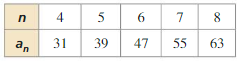
Answer:
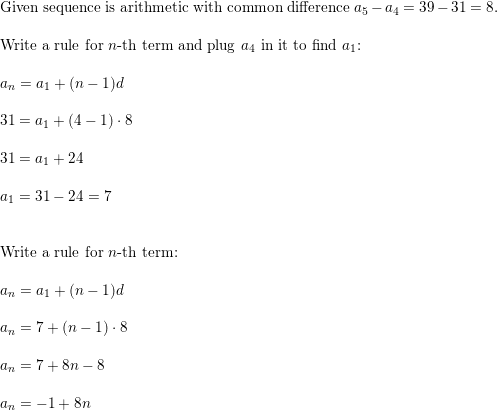
Question 45.
WRITING
Compare the graph of an = 3n + 1, where n is a positive integer, with the graph of f(x) = 3x+ 1, where x is a real number.
Answer:
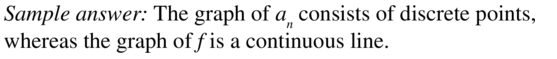
Question 46.
DRAWING CONCLUSIONS
Describe how doubling each term in an arithmetic sequence changes the common difference of the sequence. Justify your answer.
Answer:
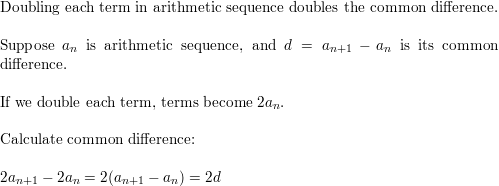
In Exercises 47–52, find the sum.
Question 47.
\(\sum_{i=1}^{20}\)(2i − 3)
Answer:

Question 48.
\(\sum_{i=1}^{26}\)(4i + 7)
Answer:
Step1: Find the first and last terms.
a1 = 4(1) + 7 = 11.
a26 = 4(26) + 7 = 111.
Step2: Find the sum
S29 = 29(11 + 111/2)
= 29(61)
S29 = 1,769
Question 49.
\(\sum_{i=1}^{33}\)(6 − 2i )
Answer:

Question 50.
\(\sum_{i=1}^{31}\)(−3 − 4i )
Answer:
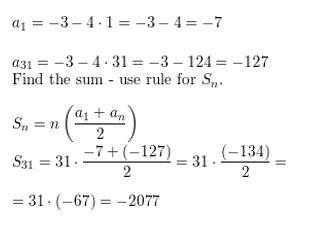
Question 51.
\(\sum_{i=1}^{41}\)(−2.3 + 0.1i )
Answer:

Question 52.
\(\sum_{i=1}^{39}\)(−4.1 + 0.4i )
Answer:
Step1: Find the first and last terms
a1 = -4.1 + 0.4(1) = -3.7
a39 = -4.1 + 0.4(39) = 11.5
Step2: Find the sum
S39 = 39(-3.7 + 11.5/2)
= 39(3.9)
S39 = 152.1
NUMBER SENSE In Exercises 53 and 54, find the sum of the arithmetic sequence.
Question 53.
The first 19 terms of the sequence 9, 2, −5, −12, . . ..
Answer:

Question 54.
The first 22 terms of the sequence 17, 9, 1, −7, . . ..
Answer:

Question 55.
MODELING WITH MATHEMATICS
A marching band is arranged in rows. The first row has three band members, and each row after the first has two more band members than the row before it.
a. Write a rule for the number of band members in the nth row.
b. How many band members are in a formation with seven rows?

Answer:

Question 56.
MODELING WITH MATHEMATICS
Domestic bees make their honeycomb by starting with a single hexagonal cell, then forming ring after ring of hexagonal cells around the initial cell, as shown. The number of cells in successive rings forms an arithmetic sequence.
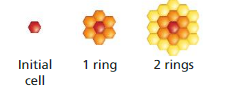
a. Write a rule for the number of cells in the nth ring.
b. How many cells are in the honeycomb after the ninth ring is formed?
Answer:

Question 57.
MATHEMATICAL CONNECTIONS
A quilt is made up of strips of cloth, starting with an inner square surrounded by rectangles to form successively larger squares. The inner square and all rectangles have a width of 1 foot. Write an expression using summation notation that gives the sum of the areas of all the strips of cloth used to make the quilt shown. Then evaluate the expression.

Answer:

Question 58.
HOW DO YOU SEE IT?
Which graph(s) represents an arithmetic sequence? Explain your reasoning.
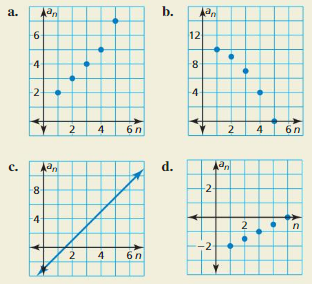
Answer:

Question 59.
MAKING AN ARGUMENT
Your friend believes the sum of a series doubles when the common difference of an arithmetic series is doubled and the first term and number of terms in the series remain unchanged. Is your friend correct? Explain your reasoning.
Answer:

Question 60.
THOUGHT PROVOKING
In number theory, the Dirichlet Prime Number Theorem states that if a and bare relatively prime, then the arithmetic sequence
a, a + b, a + 2b, a + 3b, . . . contains infinitely many prime numbers. Find the first 10 primes in the sequence when a = 3 and b = 4.
Answer:

Question 61.
REASONING
Find the sum of the positive odd integers less than 300. Explain your reasoning.
Answer:

Question 62.
USING EQUATIONS
Find the value of n.
a. \(\sum_{i=1}^{n}\)(3i + 5) = 544
Answer:
\(\sum_{i=1}^{n}\)(3i + 5) = 544
3 \(\sum_{i=1}^{n}\)(i + 5n) = 544
3n(n + 1)/2 + 5n = 544
(3n² + 13n)/2 + 5n = 544
3n² + 13n – 1088 = 0
(3n + 64) (n – 17) = 0
n = 17
n = -64/3
n = -64/3 is a negative value.
So, it is not possible
n = 17
Thus the value of n is 17.
b. \(\sum_{i=1}^{n}\)(−4i − 1) = −1127
Answer:
\(\sum_{i=1}^{n}\)(−4i − 1) = −1127
-4(n)(n + 1)/2 – n = -1127
2n(n + 1) + n = 1127
2n² + 3n – 1127 = 0
(n – 23) (2n + 49) = 0
n = 23
n = -49/2
n = -49/2 is a negatuve value.
So, it is not possible
n = 23.
c. \(\sum_{i=5}^{n}\)(7 + 12i) = 455
Answer:
\(\sum_{i=5}^{n}\)(7 + 12i) = 455
(7 + 12(5)) + (7 + 12(6)) + ….(7 + 12n) = 455
7n – 28 + 6n² + 6n – 120 = 455
6n² + 13n – 603 = 0
(n – 9) (6n + 67) = 0
n = 9 or n = -67/6
n = -67/6 is a negatuve value.
So, it is not possible
n = 9.
d. \(\sum_{i=3}^{n}\)(−3 − 4i) = −507
Answer:
\(\sum_{i=3}^{n}\)(−3 − 4i) = −507
(-3 – 4(3)) + (-3 – 4(4)) + …. + (-3 – 4n) = -507
-3(n – 2) – 4(n – 2)(3 + n)/2 = -507
-3(n – 2) – 2(n – 2) (n + 3) = 507
3n – 6 + 2n² + 2n – 12 = 507
2n² + 5n – 525 = 0
(n – 15)(2n + 35) = 0
n = 15 or n = -35/2
n = -35/2 is a negatuve value.
So, it is not possible
n = 15.
Question 63.
ABSTRACT REASONING
A theater has n rows of seats, and each row has d more seats than the row in front of it. There are x seats in the last (nth) row and a total of y seats in the entire theater. How many seats are in the front row of the theater? Write your answer in terms of n, x, and y.
Answer:

Question 64.
CRITICAL THINKING
The expressions 3 −x, x, and 1 − 3x are the first three terms in an arithmetic sequence. Find the value of x and the next term in the sequence.
Answer:
Consider 3 – x, x, 1 – 3x are in A.P.
x – (3 – x) = x – 3x – x
x – 3 + x = 1 – 4x
2x – 3 = 1 – 4x
2x + 4x = 1 + 3
6x = 4
x = 2/3
The next term is 3 – x, x, 1 – 3x
a4 = a + 3d
3 – x + 3(2x – 3)
3 – x + 6x – 9
-6 + 5x
-6 × 5 × (2/3)
-6 + 10/3
-18 + 10/3
a4 = -8/3
The value of x is 2/3 and next term in the sequence is -8/3.
Question 65.
CRITICAL THINKING
One of the major sources of our knowledge of Egyptian mathematics is the Ahmes papyrus, which is a scroll copied in 1650 B.C. by an Egyptian scribe. The following problem is from the Ahmes papyrus.
Divide 10 hekats of barley among 10 men so that the common difference is \(\frac{1}{8}\) of a hekat of barley.
Use what you know about arithmetic sequences and series to determine what portion of a hekat each man should receive.
Answer:

Maintaining Mathematical Proficiency
Simplify the expression.
Question 66.
\(\frac{7}{7^{1 / 3}}\)
Answer:
\(\frac{7}{7^{1 / 3}}\)
7/7-3
7 × 7 × 7 × 7 = 2401
Question 67.
\(\frac{3^{-2}}{3^{-4}}\)
Answer:
![]()
Question 68.
\(\left(\frac{9}{49}\right)^{1 / 2}\)
Answer:
\(\left(\frac{9}{49}\right)^{1 / 2}\)
√(9/49) = 3/7
Question 69.
(51/2 • 51/4)
Answer:
![]()
Tell whether the function represents exponential growth or exponential decay. Then graph the function.
Question 70.
y= 2ex
Answer:
Question 71.
y = e-3x
Answer:
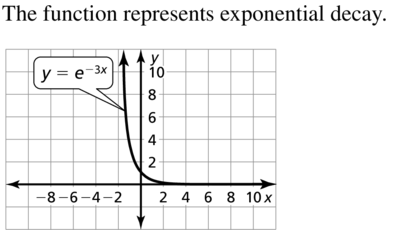
Question 72.
y = 3e-x
Answer:
Question 73.
y = e0.25x
Answer:
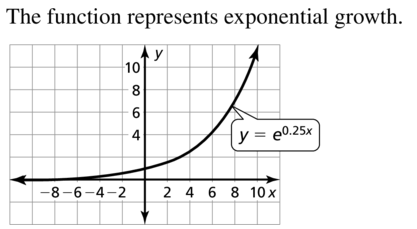
Lesson 8.3 Analyzing Geometric Sequences and Series
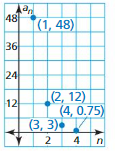
Essential Question How can you recognize a geometric sequence from its graph?
In a geometric sequence, the ratio of any term to the previous term, called the common ratio, is constant. For example, in the geometric sequence 1, 2, 4, 8, . . . , the common ratio is 2.
EXPLORATION 1
Recognizing Graphs of Geometric Sequences
Work with a partner. Determine whether each graph shows a geometric sequence. If it does, then write a rule for the nth term of the sequence and use a spreadsheet to find the sum of the first 20 terms. What do you notice about the graph of a geometric sequence?
EXPLORATION 2
Finding the Sum of a Geometric Sequence
Work with a partner. You can write the nth term of a geometric sequence with first term a1 and common ratio r as
an = a1rn-1.
So, you can write the sum Sn of the first n terms of a geometric sequence as
Sn = a1 + a1r + a1r2 + a1r3 + . . . +a1rn-1.

Rewrite this formula by finding the difference Sn − rSn and solve for Sn. Then verify your rewritten formula by funding the sums of the first 20 terms of the geometric sequences in Exploration 1. Compare your answers to those you obtained using a spreadsheet.
Communicate Your Answer
Question 3.
How can you recognize a geometric sequence from its graph?
Answer:
In general most of the curve represents geometric sequences. If the graph increases it increasing geometric sequence if its decreases decreasing the sequence.
Question 4.
Find the sum of the terms of each geometric sequence.
a. 1, 2, 4, 8, . . . , 8192
b. 0.1, 0.01, 0.001, 0.0001, . . . , 10-10
Answer:
a. tn = arn-1
tn = 8192, a = 1 and r = 2
8192 = 1 × 2n-1
213 = 2n-1
n = 14
Sn = a(rn – 1) × 1/r – 1
Sn = 1(16384 – 1) × 1/2-1
Sn = 16383
b. 0.1, 0.01, 0.001, 0.0001, . . . , 10-10
an = 10^-10
r = 0.01/0.1 = 1/10
10-10 = 1 . (1/10)n-1
(1/10)10 = 1/10n-1
10 = n – 1
n – 1 = 10
n = 11
Sn = a1/1 – r
Sn = 0.1/0.9
Sn = 1/9
Monitoring Progress
Tell whether the sequence is geometric. Explain your reasoning.
Question 1.
27, 9, 3, 1, \(\frac{1}{3}\), . . .
Answer:

Question 2.
2, 6, 24, 120, 720, . . .
Answer:

Question 3.
−1, 2, −4, 8, −16, . . .
Answer:

Question 4.
Write a rule for the nth term of the sequence 3, 15, 75, 375, . . .. Then find a9.
Answer:

Write a rule for the nth term of the sequence. Then graph the first six terms of the sequence.
Question 5.
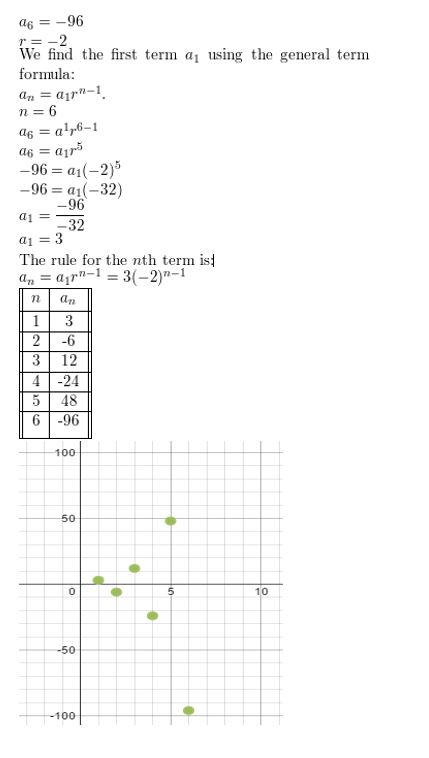
a6 = −96, r = −2
Answer:
Question 6.
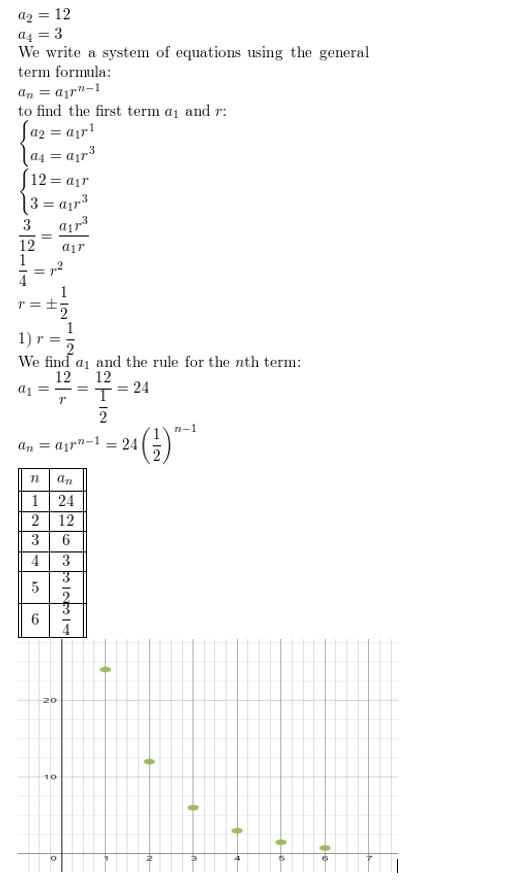
a2 = 12, a4 = 3
Answer:
Find the sum.
Question 7.
\(\sum_{k=1}^{8}\)5k−1
Answer:

Question 8.
\(\sum_{i=1}^{12}\)6(−2)i−1
Answer:

Question 9.
\(\sum_{i=1}^{7}\)−16(0.5)t−1
Answer:

Question 10.
WHAT IF?
In Example 6, how does the monthly payment change when the annual interest rate is 5%?
Answer:

Analyzing Geometric Sequences and Series 8.3 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The constant ratio of consecutive terms in a geometric sequence is called the __________.
Answer:
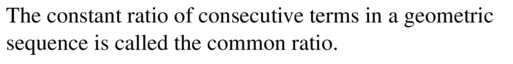
Question 2.
WRITING
How can you determine whether a sequence is geometric from its graph?
Answer:
Graph of a geometric sequence behaves like graph of exponential function.
Question 3.
COMPLETE THE SENTENCE
The nth term of a geometric sequence has the form an = ___________.
Answer:
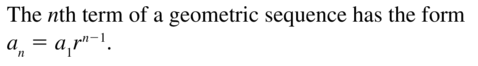
Question 4.
VOCABULARY
State the rule for the sum of the first n terms of a geometric series.
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 5–12, tell whether the sequence is geometric. Explain your reasoning.
Question 5.
96, 48, 24, 12, 6, . . .
Answer:
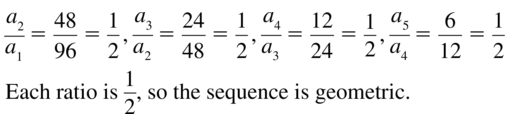
Question 6.
729, 243, 81, 27, 9, . . .
Answer:

Question 7.
2, 4, 6, 8, 10, . . .
Answer:

Question 8.
5, 20, 35, 50, 65, . . .
Answer:
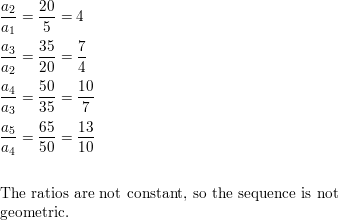
Question 9.
0.2, 3.2, −12.8, 51.2, −204.8, . . .
Answer:
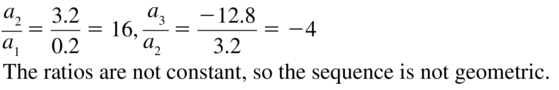
Question 10.
0.3, −1.5, 7.5, −37.5, 187.5, . . .
Answer:
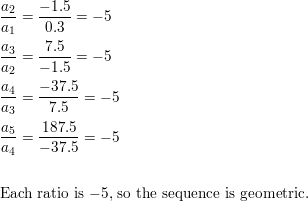
Question 11.
\(\frac{1}{2}, \frac{1}{6}, \frac{1}{18}, \frac{1}{54}, \frac{1}{162}, \ldots\)
Answer:

Question 12.
\(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}, \frac{1}{1024}, \ldots\)
Answer:
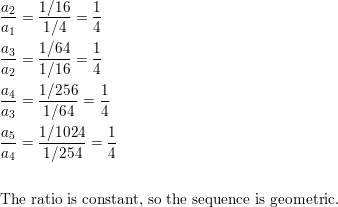
Question 13.
WRITING EQUATIONS
Write a rule for the geometric sequence with the given description.
a. The first term is −3, and each term is 5 times the previous term.
b. The first term is 72, and each term is \(\frac{1}{3}\) times the previous term.
Answer:

Question 14.
WRITING
Compare the terms of a geometric sequence when r > 1 to when 0 < r < 1.
Answer:
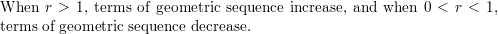
In Exercises 15–22, write a rule for the nth term of the sequence. Then find a7.
Question 15.
4, 20, 100, 500, . . .
Answer:

Question 16.
6, 24, 96, 384, . . .
Answer:
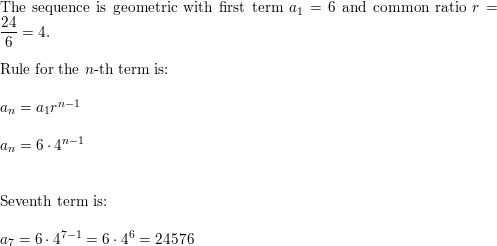
Question 17.
112, 56, 28, 14, . . .
Answer:

Question 18.
375, 75, 15, 3, . . .
Answer:
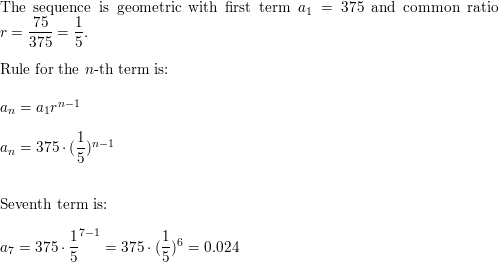
Question 19.
4, 6, 9, \(\frac{27}{2}\), . . .
Answer:

Question 20.
2, \(\frac{3}{2}\), \(\frac{9}{8}\), \(\frac{27}{32}\), . . .
Answer:

Question 21.
1.3, −3.9, 11.7, −35.1, . . .
Answer:
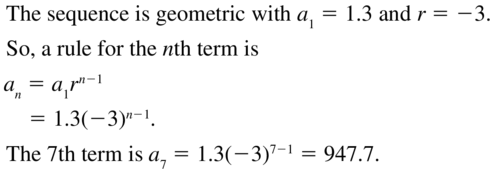
Question 22.
1.5, −7.5, 37.5, −187.5, . . .
Answer:
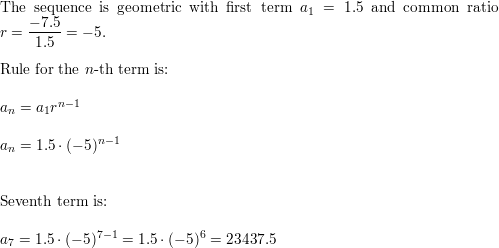
In Exercises 23–30, write a rule for the nth term of the sequence. Then graph the first six terms of the sequence.
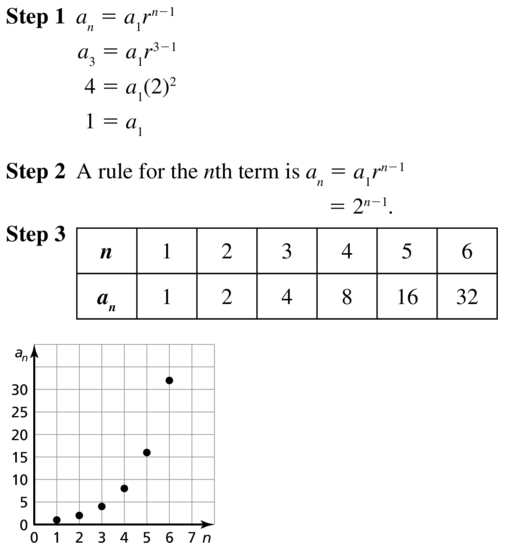
Question 23.
a3 = 4, r = 2
Answer:
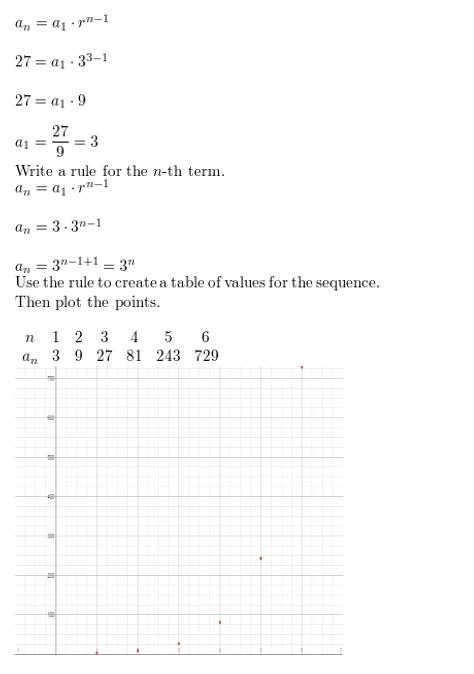
Question 24.
a3 = 27, r = 3
Answer:
Question 25.
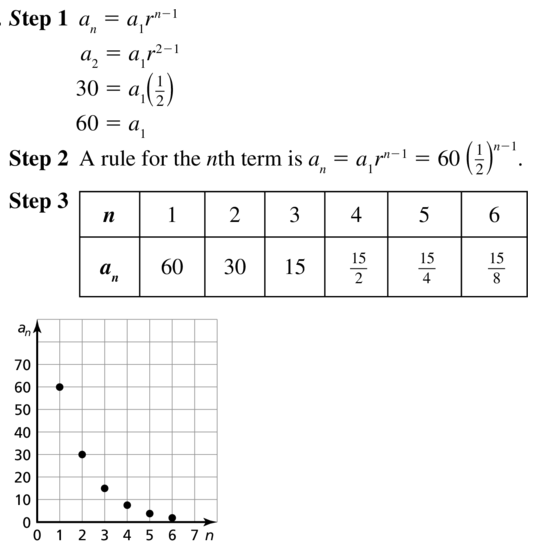
a2 = 30, r = \(\frac{1}{2}\)
Answer:
Question 26.
a2 = 64, r = \(\frac{1}{4}\)
Answer:

Question 27.
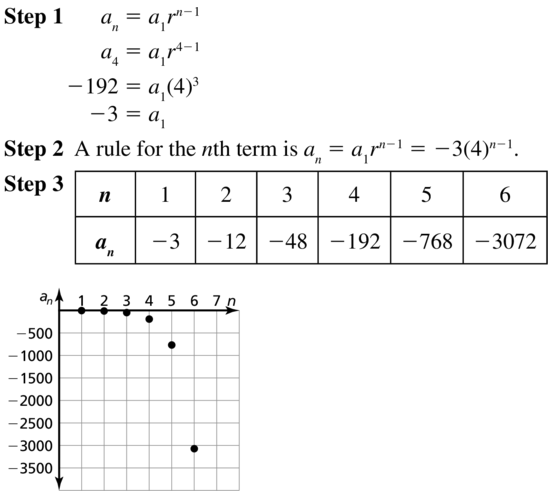
a4 = −192, r = 4
Answer:
Question 28.
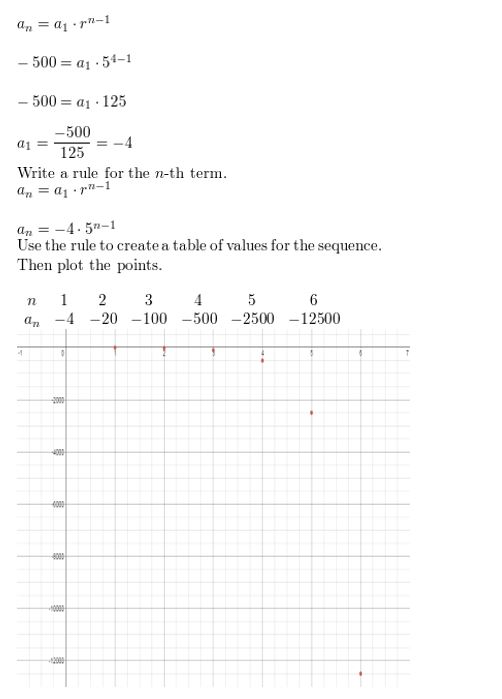
a4 = −500, r = 5
Answer:
Question 29.
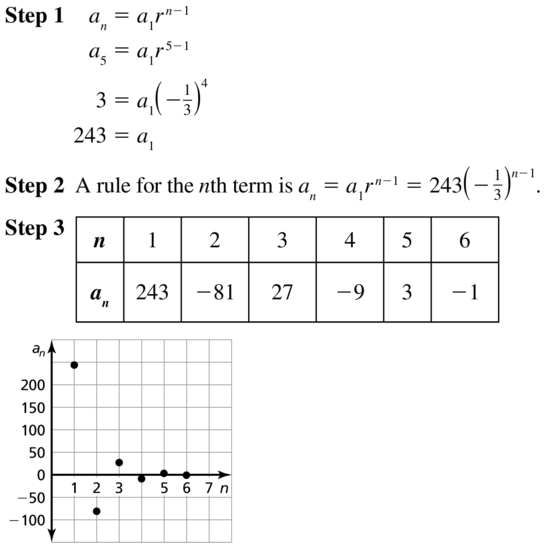
a5 = 3, r =− \(\frac{1}{3}\)
Answer:
Question 30.
a5 = 1, r = −\(\frac{1}{5}\)
Answer:
ERROR ANALYSIS In Exercises 31 and 32, describe and correct the error in writing a rule for the nth term of the geometric sequence for which a2 = 48 and r = 6.
Question 31.
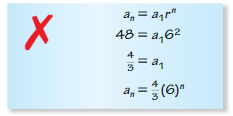
Answer:

Question 32.

Answer:

In Exercises 33–40, write a rule for the nth term of the geometric sequence.
Question 33.
a2 = 28, a5 = 1792
Answer:

Question 34.
a1 = 11, a4 = 88
Answer:
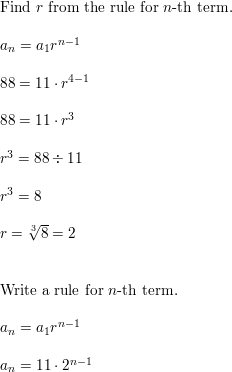
Question 35.
a1 =−6, a5 = −486
Answer:
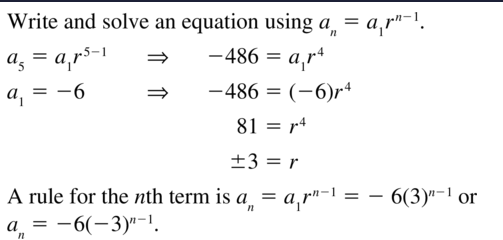
Question 36.
a2 = −10, a6 =−6250
Answer:
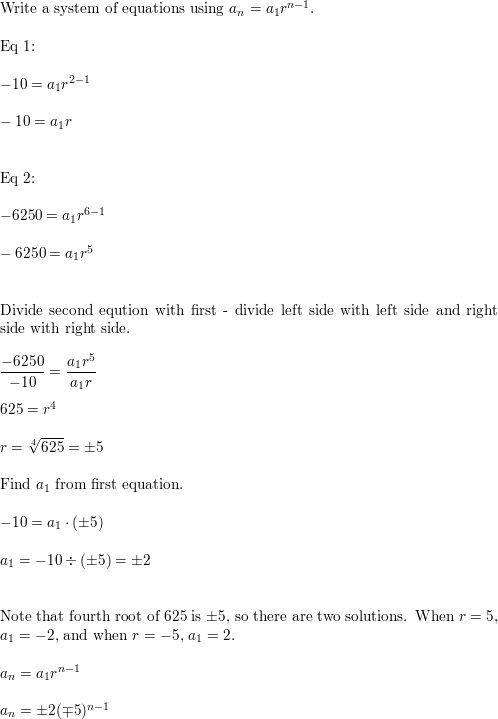
Question 37.
a2 = 64, a4 = 1
Answer:

Question 38.
a1 = 1, a2 = 49
Answer:

Question 39.
a2 =−72, a6 = −\(\frac{1}{18}\)
Answer:

Question 40.
a2 =−48, a5 = \(\frac{3}{4}\)
Answer:
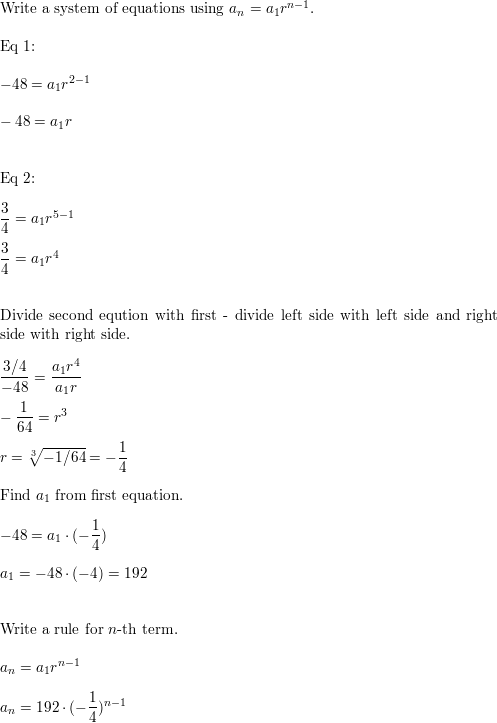
WRITING EQUATIONS In Exercises 41–46, write a rule for the sequence with the given terms.
Question 41.
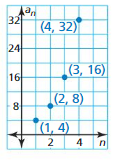
Answer:
Question 42.
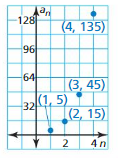
Answer:

Question 43.
Answer:
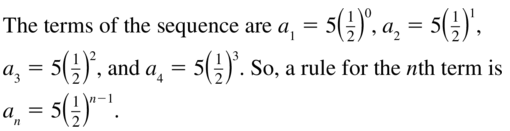
Question 44.
Answer:

Question 45.
Answer:
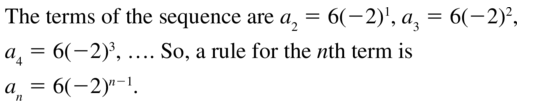
Question 46.
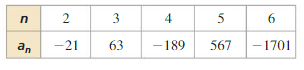
Answer:
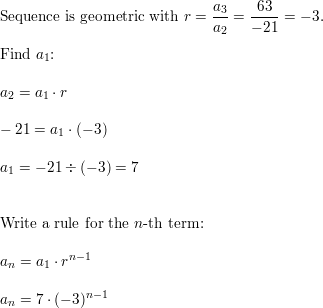
In Exercises 47–52, find the sum.
Question 47.
\(\sum_{i=1}^{9}\)6(7)i−1
Answer:

Question 48.
\(\sum_{i=1}^{10}\)7(4)i−1
Answer:
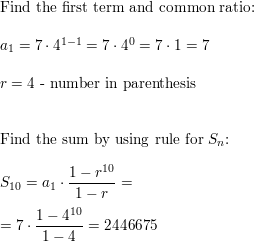
Question 49.
\(\sum_{i=1}^{10}\)4(\(\frac{3}{4}\))i−1
Answer:

Question 50.
\(\sum_{i=1}^{8}\)5(\(\frac{1}{3}\))i−1
Answer:
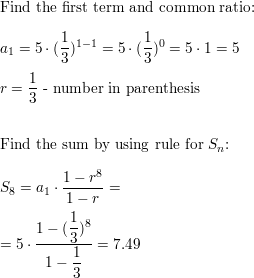
Question 51.
\(\sum_{i=0}^{8}\)8(−\(\frac{2}{3}\))i
Answer:

Question 52.
\(\sum_{i=0}^{0}\)9(−\(\frac{3}{4}\))i
Answer:
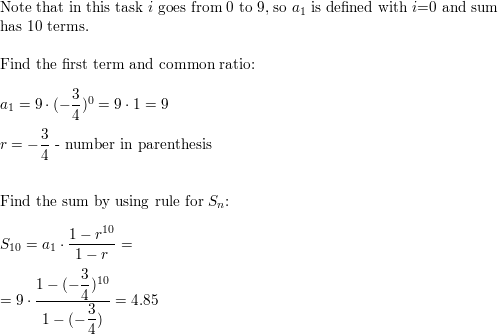
NUMBER SENSE In Exercises 53 and 54, find the sum.
Question 53.
The first 8 terms of the geometric sequence −12, −48, −192, −768, . . ..
Answer:

Question 54.
The first 9 terms of the geometric sequence −14, −42, −126, −378, . . ..
Answer:
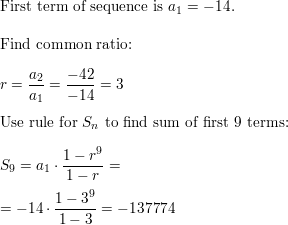
Question 55.
WRITING
Compare the graph of an = 5(3)n−1, where n is a positive integer, to the graph of f(x) = 5 • 3x−1, where x is a real number.
Answer:
Question 56.
ABSTRACT REASONING
Use the rule for the sum of a finite geometric series to write each polynomial as a rational expression.
a. 1 + x + x2 + x3 + x4
b. 3x + 6x3 + 12x5 + 24x7
Answer:

MODELING WITH MATHEMATICS In Exercises 57 and 58, use the monthly payment formula given in Example 6.
Question 57.
You are buying a new car. You take out a 5-year loan for $15,000. The annual interest rate of the loan is 4%. Calculate the monthly payment.
Answer:

Question 58.
You are buying a new house. You take out a 30-year mortgage for $200,000. The annual interest rate of the loan is 4.5%. Calculate the monthly payment.

Answer:
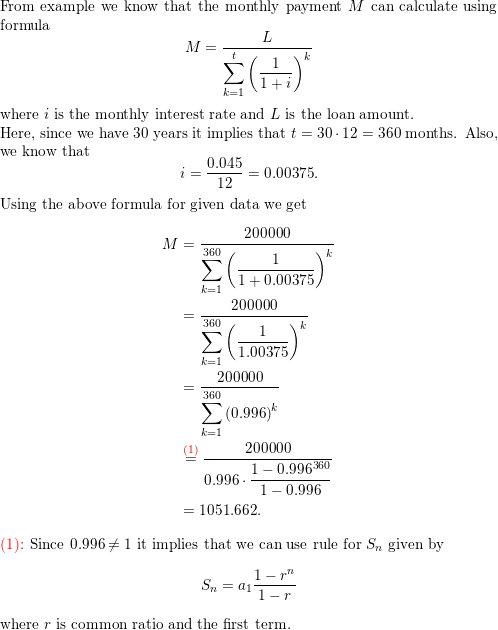
Question 59.
MODELING WITH MATHEMATICS
A regional soccer tournament has 64 participating teams. In the first round of the tournament, 32 games are played. In each successive round, the number of games decreases by a factor of \(\frac{1}{2}\).
a. Write a rule for the number of games played in the nth round. For what values of n does the rule make sense? Explain.
b. Find the total number of games played in the regional soccer tournament.
Answer:

Question 60.
MODELING WITH MATHEMATICS
In a skydiving formation with R rings, each ring after the first has twice as many skydivers as the preceding ring. The formation for R = 2 is shown.

a. Let an be the number of skydivers in the nth ring. Write a rule for an.
b. Find the total number of skydivers when there are four rings.
Answer:

Question 61.
PROBLEM SOLVING
The Sierpinski carpet is a fractal created using squares. The process involves removing smaller squares from larger squares. First, divide a large square into nine congruent squares. Then remove the center square. Repeat these steps for each smaller square, as shown below. Assume that each side of the initial square is 1 unit long.
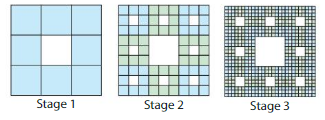
a. Let an be the total number of squares removed at the nth stage. Write a rule for an. Then find the total number of squares removed through Stage 8.
b. Let bn be the remaining area of the original square after the nth stage. Write a rule for bn. Then find the remaining area of the original square after Stage 12.
Answer:

Question 62.
HOW DO YOU SEE IT?
Match each sequence with its graph. Explain your reasoning.
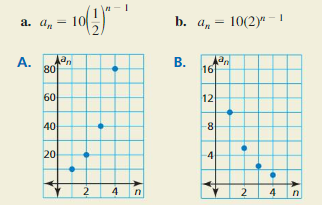
Answer:

Question 63.
CRITICAL THINKING
On January 1, you deposit $2000 in a retirement account that pays 5% annual interest. You make this deposit each January 1 for the next 30 years. How much money do you have in your account immediately after you make your last deposit?
Answer:
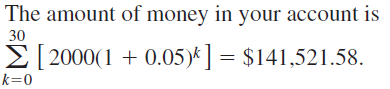
Question 64.
THOUGHT PROVOKING
The first four iterations of the fractal called the Koch snowflake are shown below. Find the perimeter and area of each iteration. Do the perimeters and areas form geometric sequences? Explain your reasoning.
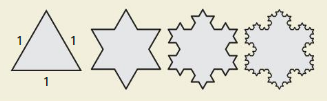
Answer:

Question 65.
MAKING AN ARGUMENT
You and your friend are comparing two loan options for a $165,000 house. Loan 1 is a 15-year loan with an annual interest rate of 3%. Loan 2 is a 30-year loan with an annual interest rate of 4%. Your friend claims the total amount repaid over the loan will be less for Loan 2. Is your friend correct? Justify your answer.
Answer:

Question 66.
CRITICAL THINKING
Let L be the amount of a loan (in dollars), i be the monthly interest rate (in decimal form), t be the term (in months), and M be the monthly payment (in dollars).
a. When making monthly payments, you are paying the loan amount plus the interest the loan gathers each month. For a 1-month loan, t= 1, the equation for repayment is L(1 +i) −M= 0. For a 2-month loan, t= 2, the equation is [L(1 + i) −M](1 + i) −M = 0. Solve both of these repayment equations for L.
b. Use the pattern in the equations you solved in part (a) to write a repayment equation for a t-month loan. (Hint: L is equal to M times a geometric series.) Then solve the equation for M.
c. Use the rule for the sum of a finite geometric series to show that the formula in part (b) is equivalent to
M = L\(\left(\frac{i}{1-(1+i)^{-t}}\right)\).
Use this formula to check your answers in Exercises 57 and 58.
Answer:

Maintaining Mathematical Proficiency
Graph the function. State the domain and range.
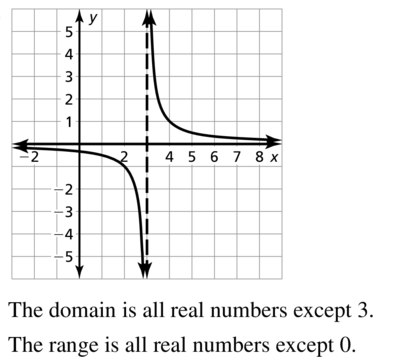
Question 67.
f(x) = \(\frac{1}{x-3}\)
Answer:
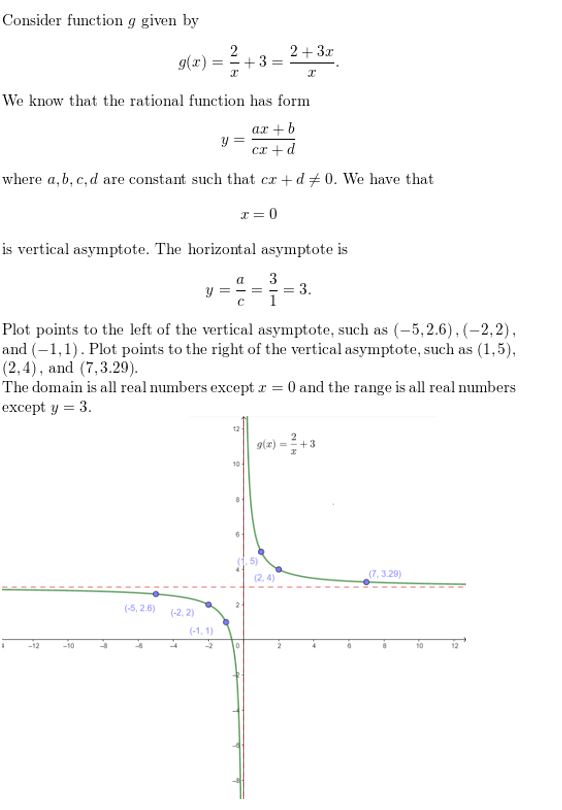
Question 68.
g(x) = \(\frac{2}{x}\) + 3
Answer:
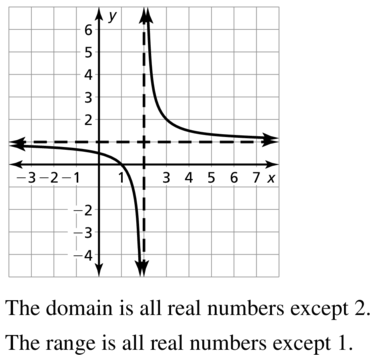
Question 69.
h(x) = \(\frac{1}{x-2}\) + 1
Answer:
Question 70.
p(x) = \(\frac{3}{x+1}\) − 2
Answer:
Sequences and Series Study Skills: Keeping Your Mind Focused
8.1–8.3 What Did You Learn?
Core Vocabulary

Core Concepts
Section 8.1Sequences, p. 410
Series and Summation Notation, p. 412
Formulas for Special Series, p. 413
Section 8.2
Rule for an Arithmetic Sequence, p. 418
The Sum of a Finite Arithmetic Series, p. 420
Section 8.3
Rule for a Geometric Sequence, p. 426
The Sum of a Finite Geometric Series, p. 428
Mathematical Practices
Question 1.
Explain how viewing each arrangement as individual tables can be helpful in Exercise 29 on page 415.
Answer:
Question 2.
How can you use tools to find the sum of the arithmetic series in Exercises 53 and 54 on page 423?
Answer:
Question 3.
How did understanding the domain of each function help you to compare the graphs in Exercise 55 on page 431?
Answer:
Study Skills: Keeping Your Mind Focused
• Before doing homework, review the concept boxes and examples. Talk through the examples out loud.
• Complete homework as though you were also preparing for a quiz. Memorize the different types of problems, formulas, rules, and so on.

Sequences and Series 8.1 – 8.3 Quiz
Describe the pattern, write the next term, and write a rule for the nth term of the sequence.
Question 1.
1, 7, 13, 19, . . .
Answer:

Question 2.
−5, 10, −15, 20, . . .
Answer:

Question 3.
\(\frac{1}{20}, \frac{2}{30}, \frac{3}{40}, \frac{4}{50}, \ldots\)
Answer:
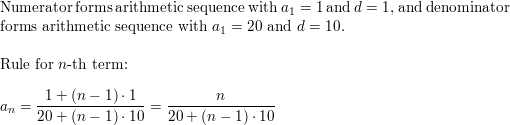
Write the series using summation notation. Then find the sum of the series.
Question 4.
1 + 2 + 3 + 4 +. . .+ 15
Answer:
Question 5.
\(0+\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots+\frac{7}{8}\)
Answer:

Question 6.
9 + 16 + 25 + . . .+ 100
Answer:

Write a rule for the nth term of the sequence.
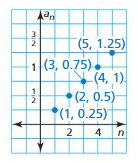
Question 7.
Answer:

Question 8.
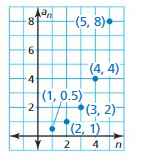
Answer:

Question 9.
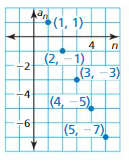
Answer:
Tell whether the sequence is arithmetic, geometric, or neither. Write a rule for the nth term of the sequence. Then find a9.
Question 10.
13, 6, −1, −8, . . .
Answer:
Question 11.
\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots\)
Answer:

Question 12.
1, −3, 9, −27, . . .
Answer:

Question 13.
One term of an arithmetic sequence is a12 = 19. The common difference is d = 7. Write a rule for the nth term. Then graph the first six terms of the sequence.
Answer:
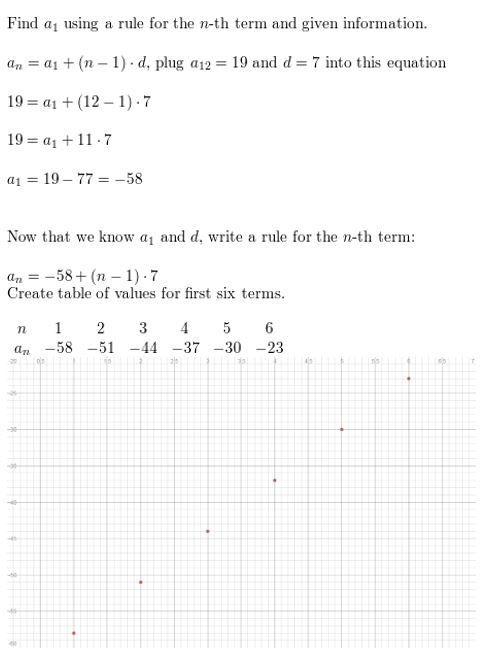
Question 14.
Two terms of a geometric sequence are a6 = −50 and a9 = −6250. Write a rule for the nth term.
Answer:

Find the sum.
Question 15.
\(\sum_{n=1}^{9}\)(3n + 5)
Answer:
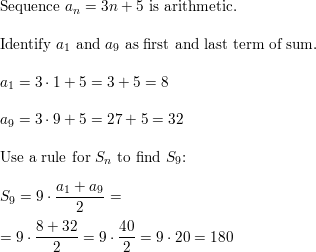
Question 16.
\(\sum_{k=1}^{5}\)11(−3)k−2
Answer:
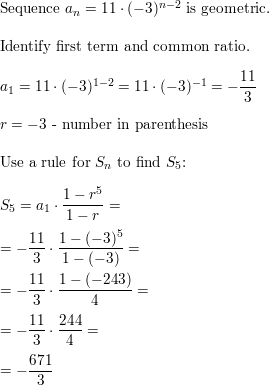
Question 17.
\(\sum_{i=1}^{12}\)−4 (\(\frac{1}{2}\))i+3
Answer:
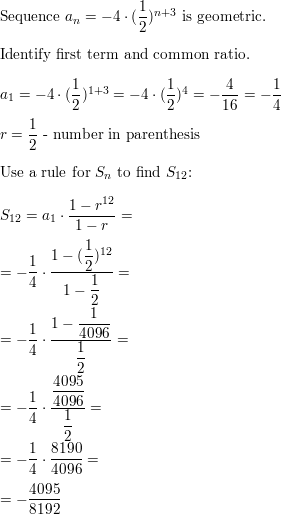
Question 18.
Pieces of chalk are stacked in a pile. Part of the pile is shown. The bottom row has 15 pieces of chalk, and the top row has 6 pieces of chalk. Each row has one less piece of chalk than the row below it. How many pieces of chalk are in the pile?

Answer:

Question 19.
You accept a job as an environmental engineer that pays a salary of $45,000 in the first year. After the first year, your salary increases by 3.5% per year.
a. Write a rule giving your salary an for your nth year of employment.
b. What will your salary be during your fifth year of employment?
c. You work 10 years for the company. What are your total earnings? Justify your answer.
Answer:

Lesson 8.4 Finding Sums of Infinite Geometric Series
Essential Question How can you find the sum of an infinite geometric series?
EXPLORATION 1
Finding Sums of Infinite Geometric Series

Work with a partner. Enter each geometric series in a spreadsheet. Then use the spreadsheet to determine whether the infinite geometric series has a finite sum. If it does, find the sum. Explain your reasoning. (The figure shows a partially completed spreadsheet for part (a).)

EXPLORATION 2
Writing a Conjecture
Work with a partner. Look back at the infinite geometric series in Exploration 1. Write a conjecture about how you can determine whether the infinite geometric series
a1 + a1r + a1r2 + a1r3 +. . .has a finite sum.
EXPLORATION 3
Writing a Formula
Work with a partner. In Lesson 8.3, you learned that the sum of the first n terms of a geometric series with first term a1 and common ratio r≠ 1 is
Sn = a1\(\left(\frac{1-r^{n}}{1-r}\right)\)
When an infinite geometric series has a finite sum, what happens to r n as n increases? Explain your reasoning. Write a formula to find the sum of an infinite geometric series. Then verify your formula by checking the sums you obtained in Exploration 1.
Communicate Your Answer
Question 4.
How can you find the sum of an infinite geometric series?
Answer:
There is an equation for it,
Sum = a1(1 – r)
a1 = the first term of the series
r = rate of change
Question 5.
Find the sum of each infinite geometric series, if it exists.
a. 1 + 0.1 + 0.01 + 0.001 + 0.0001 +. . .
b. \(2+\frac{4}{3}+\frac{8}{9}+\frac{16}{27}+\frac{32}{81}+\cdots\)
Answer:
Given,
1 + 0.1 + 0.01 + 0.001 + 0.0001 +. . .
a1 = 1
|r| < 1, the series does have a limit given by formula of limit or sum of an infinite geometric series
S∞ = a1/1-r
S∞ = 1/1 – 0.1 = 1/0.9 = 1.11…
b. \(2+\frac{4}{3}+\frac{8}{9}+\frac{16}{27}+\frac{32}{81}+\cdots\)
r = a2/a1
r = 4/3/2
r = 2/3
Each ratio is 2/3, so the sequence is geometric
a1 = 2 and r = 2/3
Sn = a1/1 – r
S = 2/(1-2/3)
S = 6
The sum of infinite geometric series S = 6.
Monitoring Progress
Question 1.
Consider the infinite geometric series
\(\frac{2}{5}+\frac{4}{25}+\frac{8}{125}+\frac{16}{1625}+\frac{32}{3125}+\cdots\)
Find and graph the partial sums Sn for n = 1, 2, 3, 4, and 5. Then describe what happens to Sn as n increases.
Answer:

Find the sum of the infinite geometric series, if it exists.
Question 2.
\(\sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^{n-1}\)
Answer:

Question 3.
\(\sum_{n=1}^{\infty} 3\left(\frac{5}{4}\right)^{n-1}\)
Answer:

Question 4.
\(3+\frac{3}{4}+\frac{3}{16}+\frac{3}{64}+\cdots\)
Answer:

Question 5.
WHAT IF?
In Example 3, suppose the pendulum travels 10 inches on its first swing. What is the total distance the pendulum swings?
Answer:

Write the repeating decimal as a fraction in simplest form.
Question 6.
0.555 . . . .
Answer:

Question 7.
0.727272 . . . .
Answer:

Question 8.
0.131313 . . . .
Answer:

Finding Sums of Infinite Geometric Series 8.4 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
The sum Sn of the first n terms of an infinite series is called a(n) ________.
Answer:
Question 2.
WRITING
Explain how to tell whether the series \(\sum_{i=1}^{\infty}\)a1ri−1 has a sum.
Answer:
Monitoring Progress and Modeling with Mathematics
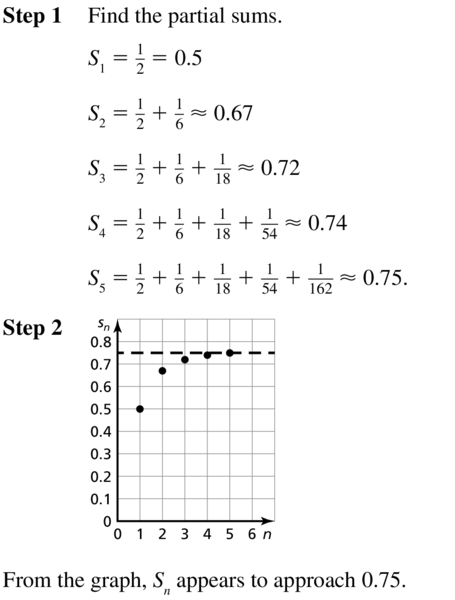
In Exercises 3–6, consider the infinite geometric series. Find and graph the partial sums Sn for n= 1, 2, 3, 4, and 5. Then describe what happens to Sn as n increases.
Question 3.
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{18}+\frac{1}{54}+\frac{1}{162}+\cdots\)
Answer:
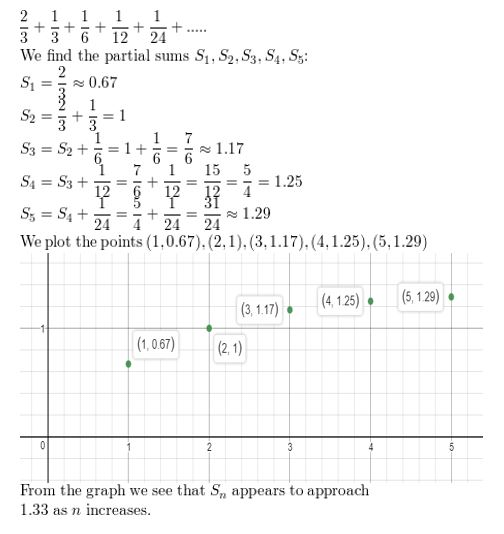
Question 4.
\(\frac{2}{3}+\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\cdots\)
Answer:
Question 5.
4 + \(\frac{12}{5}+\frac{36}{25}+\frac{108}{125}+\frac{324}{625}+\cdots\)
Answer:
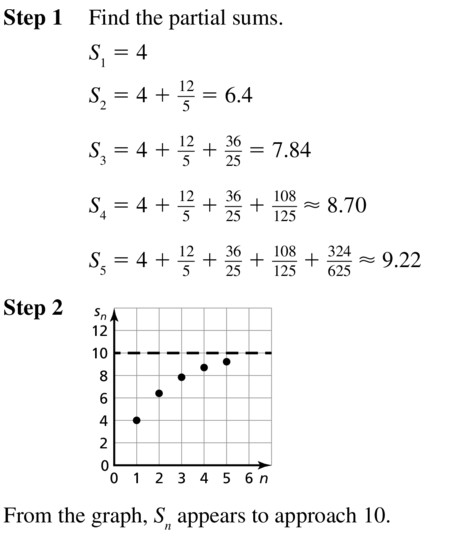
Question 6.
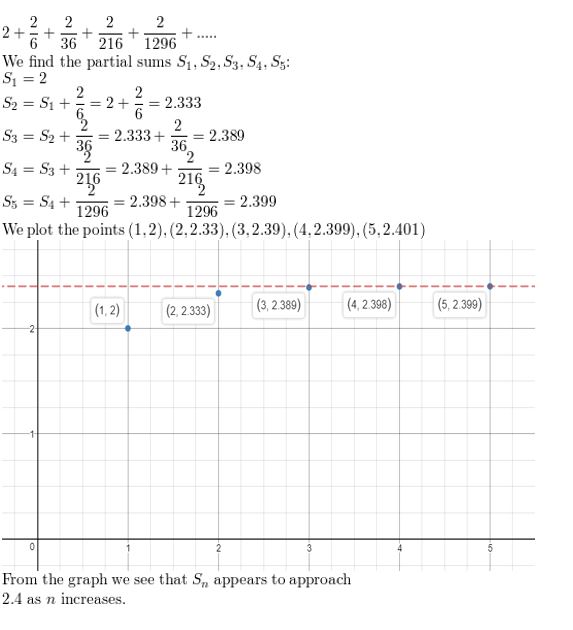
2 + \(\frac{2}{6}+\frac{2}{36}+\frac{2}{216}+\frac{2}{1296}+\cdots\)
Answer:
In Exercises 7–14, find the sum of the infinite geometric series, if it exists.
Question 7.
\(\sum_{n=1}^{\infty} 8\left(\frac{1}{5}\right)^{n-1}\)
Answer:
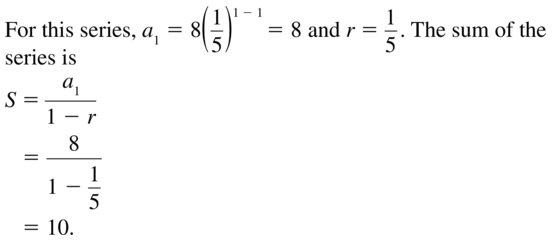
Question 8.
\(\sum_{k=1}^{\infty}-6\left(\frac{3}{2}\right)^{k-1}\)
Answer:
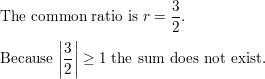
Question 9.
\(\sum_{k=1}^{\infty} \frac{11}{3}\left(\frac{3}{8}\right)^{k-1}\)
Answer:
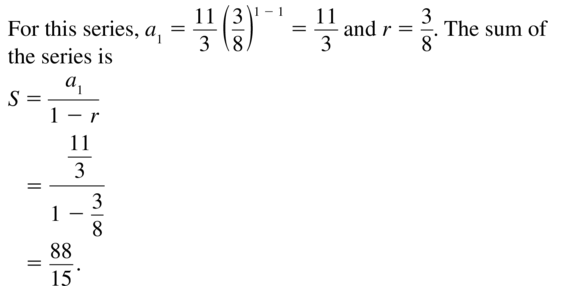
Question 10.
\(\sum_{i=1}^{\infty} \frac{2}{5}\left(\frac{5}{3}\right)^{i-1}\)
Answer:
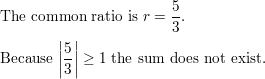
Question 11.
2 + \(\frac{6}{4}+\frac{18}{16}+\frac{54}{64}+\cdots\)
Answer:
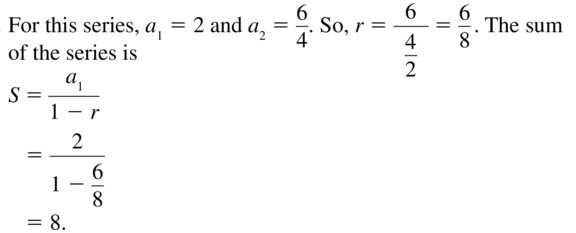
Question 12.
-5 – 2 – \(\frac{4}{5}-\frac{8}{25}-\cdots\)
Answer:
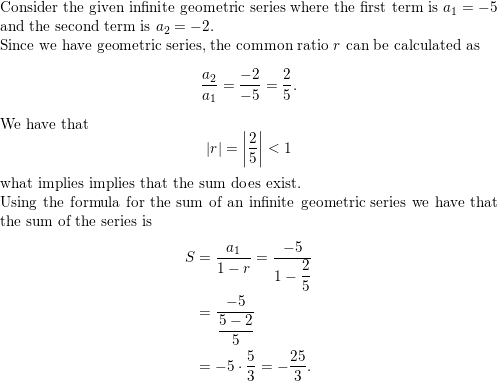
Question 13.
3 + \(\frac{5}{2}+\frac{25}{12}+\frac{125}{72}+\cdots\)
Answer:
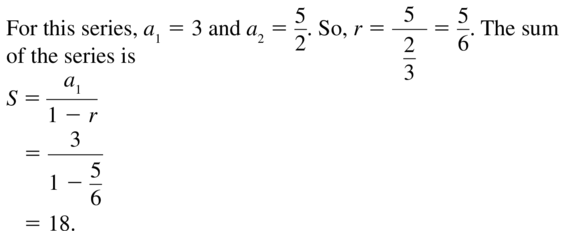
Question 14.
\(\frac{1}{2}-\frac{5}{3}+\frac{50}{9}-\frac{500}{27}+\cdots\)
Answer:
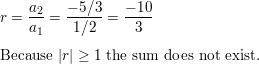
ERROR ANALYSIS In Exercises 15 and 16, describe and correct the error in finding the sum of the infinite geometric series.
Question 15.
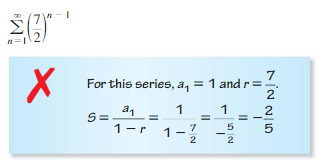
Answer:
![]()
Question 16.
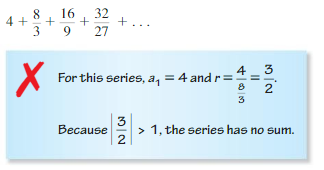
Answer:
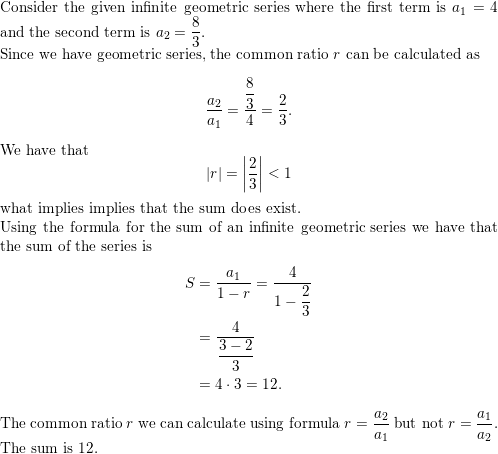
Question 17.
MODELING WITH MATHEMATICS
You push your younger cousin on a tire swing one time and then allow your cousin to swing freely. On the first swing, your cousin travels a distance of 14 feet. On each successive swing, your cousin travels 75% of the distance of the previous swing. What is the total distance your cousin swings?

Answer:

Question 18.
MODELING WITH MATHEMATICS
A company had a profit of $350,000 in its first year. Since then, the company’s profit has decreased by 12% per year. Assuming this trend continues, what is the total profit the company can make over the course of its lifetime? Justify your answer.
Answer:
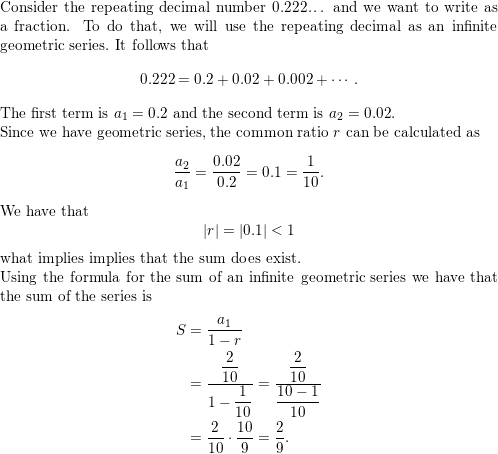
In Exercises 19–24, write the repeating decimal as a fraction in simplest form.
Question 19.
0.222 . . .
Answer:
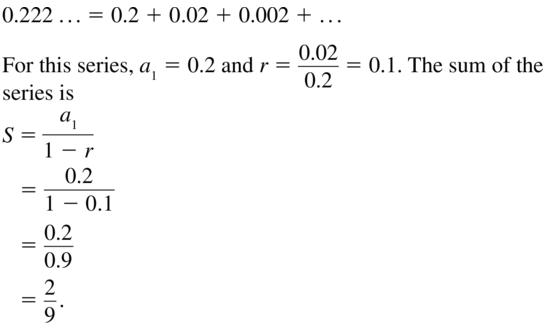
Question 20.
0.444 . . .
Answer:

Question 21.
0.161616 . . .
Answer:

Question 22.
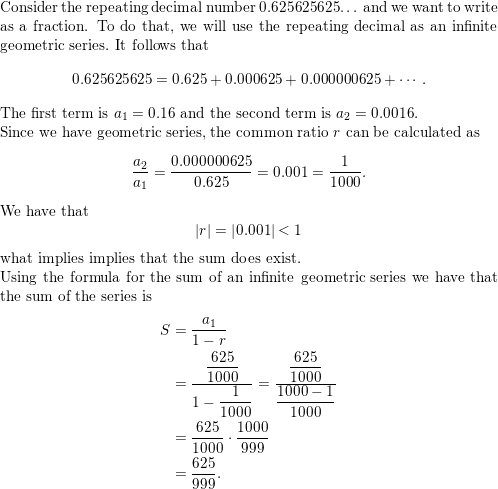
0.625625625 . . .
Answer:
Question 23.
32.323232 . . .
Answer:

Question 24.
130.130130130 . . .
Answer:
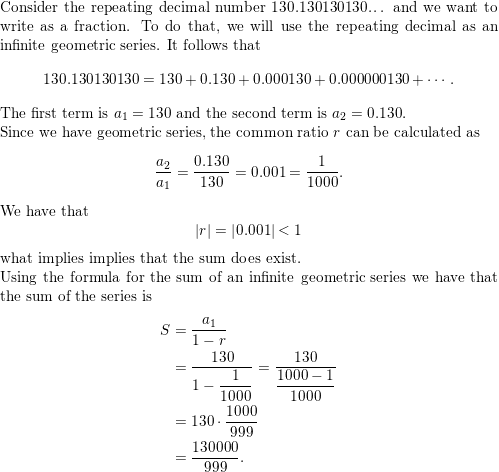
Question 25.
PROBLEM SOLVING
Find two infinite geometric series whose sums are each 6. Justify your answers.
Answer:
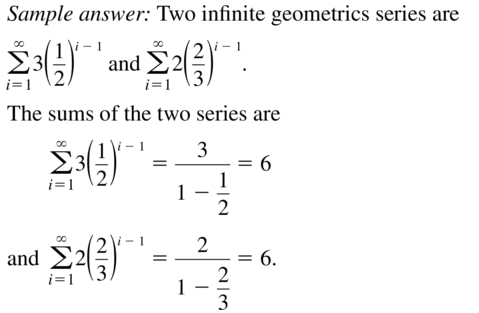
Question 26.
HOW DO YOU SEE IT?
The graph shows the partial sums of the geometric series a1 + a2 + a3 + a4+. . . .What is the value of \(\sum_{n=1}^{\infty}\)an ? Explain.
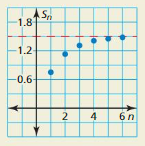
Answer:
Question 27.
MODELING WITH MATHEMATICS
A radio station has a daily contest in which a random listener is asked a trivia question. On the first day, the station gives $500 to the first listener who answers correctly. On each successive day, the winner receives 90% of the winnings from the previous day. What is the total amount of prize money the radio station gives away during the contest?
Answer:

Question 28.
THOUGHT PROVOKING
Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. In “Quadrature of the Parabola,” he proved that the area of the region is \(\frac{4}{3}\) the area of the inscribed triangle. The first term of the series for the parabola below is represented by the area of the blue triangle and the second term is represented by the area of the red triangles. Use Archimedes’ result to find the area of the region. Then write the area as the sum of an infinite geometric series.
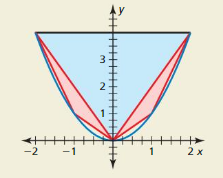
Answer:
Question 29.
DRAWING CONCLUSIONS
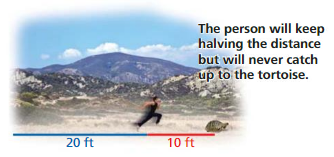
Can a person running at 20 feet per second ever catch up to a tortoise that runs 10 feet per second when the tortoise has a 20-foot head start? The Greek mathematician Zeno said no. He reasoned as follows:
Looking at the race as Zeno did, the distances and the times it takes the person to run those distances both form infinite geometric series. Using the table, show that both series have finite sums. Does the person catch up to the tortoise? Justify your answer.
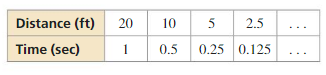
Answer:

Question 30.
MAKING AN ARGUMENT
Your friend claims that 0.999 . . . is equal to 1. Is your friend correct? Justify your answer.
Answer:
Question 31.
CRITICAL THINKING
The Sierpinski triangle is a fractal created using equilateral triangles. The process involves removing smaller triangles from larger triangles by joining the midpoints of the sides of the larger triangles as shown. Assume that the initial triangle has an area of 1 square foot.
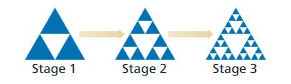
a. Let an be the total area of all the triangles that are removed at Stage n. Write a rule for an.
b. Find \(\sum_{n=1}^{\infty}\)an. Interpret your answer in the context of this situation.
Answer:

Maintaining Mathematical Proficiency
Determine the type of function represented by the table.
Question 32.
Answer:
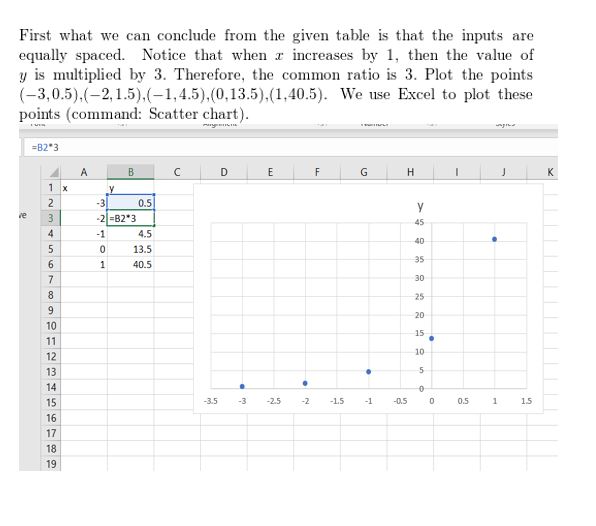
Question 33.
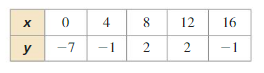
Answer:
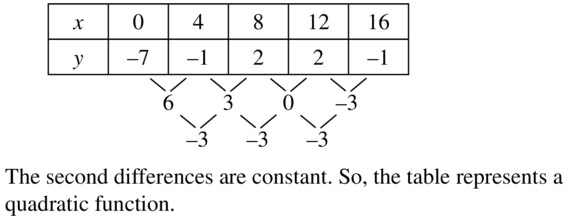
Determine whether the sequence is arithmetic, geometric, or neither.
Question 34.
−7, −1, 5, 11, 17, . . .
Answer:
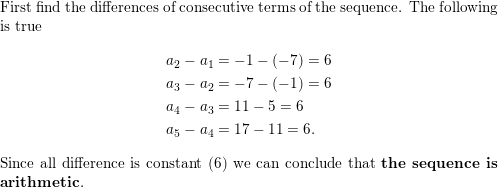
Question 35.
0, −1, −3, −7, −15, . . .
Answer:
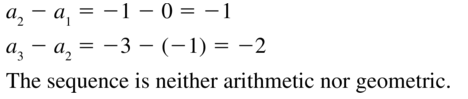
Question 36.
13.5, 40.5, 121.5, 364.5, . .
Answer:

Lesson 8.5 Using Recursive Rules with Sequences
Essential Question How can you define a sequence recursively?A recursive rule gives the beginning term(s) of a sequence and a recursive equation that tells how an is related to one or more preceding terms.
EXPLORATION 1
Evaluating a Recursive Rule
Work with a partner. Use each recursive rule and a spreadsheet to write the first six terms of the sequence. Classify the sequence as arithmetic, geometric, or neither. Explain your reasoning. (The figure shows a partially completed spreadsheet for part (a).)

EXPLORATION 2
Writing a Recursive Rule

Work with a partner. Write a recursive rule for the sequence. Explain your reasoning.
a. 3, 6, 9, 12, 15, 18, . . .
b. 18, 14, 10, 6, 2, −2, . . .
c. 3, 6, 12, 24, 48, 96, . . .
d. 128, 64, 32, 16, 8, 4, . . .
e. 5, 5, 5, 5, 5, 5, . . .
f. 1, 1, 2, 3, 5, 8, . . .
EXPLORATION 3
Writing a Recursive RuleWork with a partner. Write a recursive rule for the sequence whose graph is shown.
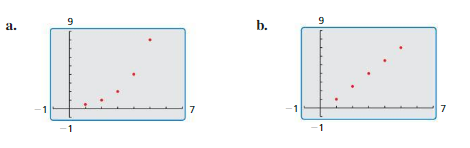
Communicate Your Answer
Question 4.
How can you define a sequence recursively?
Answer: A recursive sequence is also called the recurrence sequence it is a sequence of numbers indexed by an integer and generated by solving a recurrence equation.
Question 5.
Write a recursive rule that is different from those in Explorations 1–3. Write the first six terms of the sequence. Then graph the sequence and classify it as arithmetic, geometric, or neither.
Answer:
Monitoring Progress
Write the first six terms of the sequence.
Question 1.
a1 = 3, an = an-1 − 7
Answer:
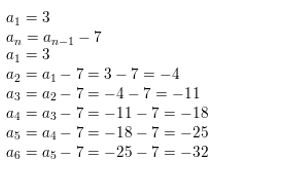
Question 2.
a0 = 162, an = 0.5an-1
Answer:
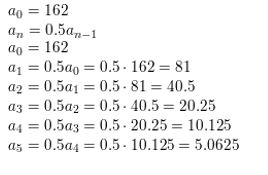
Question 3.
f(0) = 1, f(n) = f(n− 1) + n
Answer:
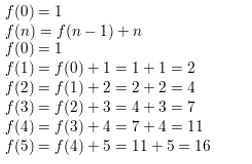
Question 4.
a1 = 4, an = 2an-1 − 1
Answer:
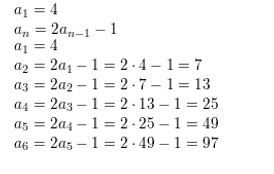
Write a recursive rule for the sequence.
Question 5.
2, 14, 98, 686, 4802, . . .
Answer:
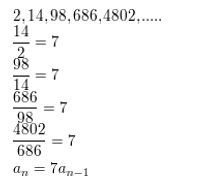
Question 6.
19, 13, 7, 1, −5, . . .
Answer:
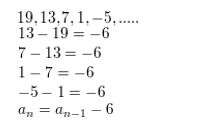
Question 7.
11, 22, 33, 44, 55, . . .
Answer:
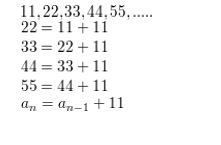
Question 8.
1, 2, 2, 4, 8, 32, . . .
Answer:
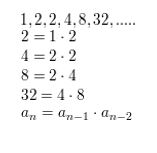
Write a recursive rule for the sequence.
Question 9.
an = 17 − 4n
Answer:
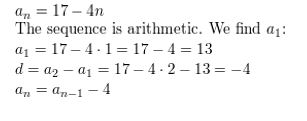
Question 10.
an = 16(3)n-1
Answer:
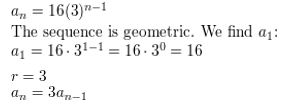
Write an explicit rule for the sequence.
Question 11.
a1 = −12, an = an-1 + 16
Answer:
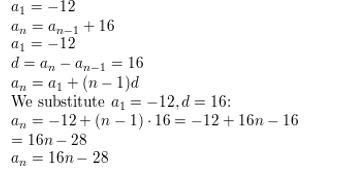
Question 12.
a1 = 2, an = −6an-1
Answer:
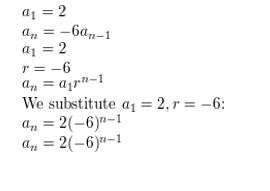
Question 13.
WHAT IF?
In Example 6, suppose 75% of the fish remain each year. What happens to the population of fish over time?
Answer:

Question 14.
WHAT IF?
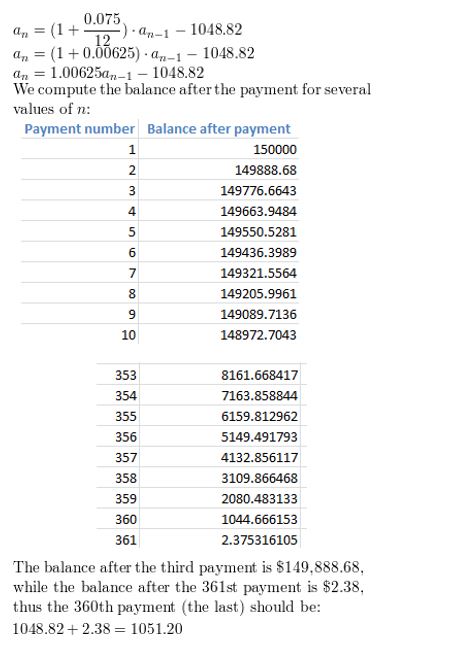
How do the answers in Example 7 change when the annual interest rate is 7.5% and the monthly payment is $1048.82?
Answer:
Using Recursive Rules with Sequences 8.5 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
A recursive _________ tells how the nth term of a sequence is related to one or more preceding terms.
Answer:

Question 2.
WRITING
Explain the difference between an explicit rule and a recursive rule for a sequence.
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, write the first six terms of the sequence.
Question 3.
a1 = 1
an = an-1 + 3
Answer:
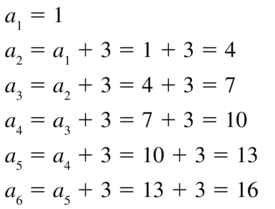
Question 4.
a1 = 1
an = an-1 − 5
Answer:
a1 = 1
an = an-1 − 5
a2 = a1 – 5 = 1-5 = -4
a3 = a2 – 5 = -4 – 5 = -9
a4 = a3 – 5 = -9 – 5 = -14
a5 = a4 – 5 = -14 – 5 = -19
a6 = a5 – 5 = -19 – 5 = -24
Question 5.
f(0) = 4
f(n) = 2f (n− 1)
Answer:
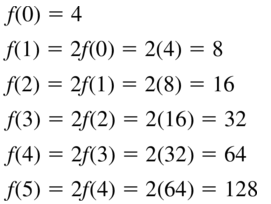
Question 6.
f(0) = 10
f(n) = \(\frac{1}{2}\)f(n− 1)
Answer:
f(0) = 10
f(n) = \(\frac{1}{2}\)f(n− 1)
f(1) = \(\frac{1}{2}\)f(0) = 1/2 × 10 = 5
f(2) = \(\frac{1}{2}\)f(1) = 1/2 × 5 = 5/2
f(3) = \(\frac{1}{2}\)f(2) = 1/2 × 5/2 = 5/4
f(4) = \(\frac{1}{2}\)f(3) = 1/2 × 5/4 = 5/8
f(5) = \(\frac{1}{2}\)f(4) = 1/2 × 5/8 = 5/16
Question 7.
a1 = 2
an = (an-1)2 + 1
Answer:
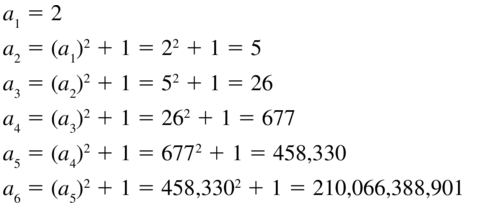
Question 8.
a1 = 1
an = (an-1)2 − 10
Answer:
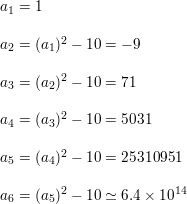
Question 9.
f(0) = 2, f (1) = 4
f(n) = f(n − 1) − f(n − 2)
Answer:
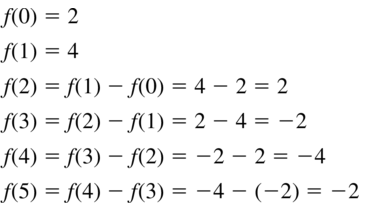
Question 10.
f(1) = 2, f(2) = 3
f(n) = f(n − 1) • f(n − 2)
Answer:
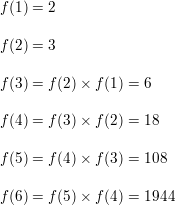
In Exercises 11–22, write a recursive rule for the sequence.
Question 11.
21, 14, 7, 0, −7, . . .
Answer:

Question 12.
54, 43, 32, 21, 10, . . .
Answer:
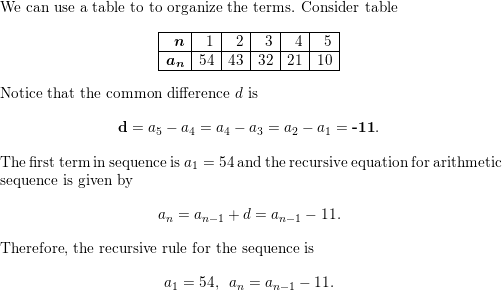
Question 13.
3, 12, 48, 192, 768, . . .
Answer:

Question 14.
4, −12, 36, −108, . . .
Answer:
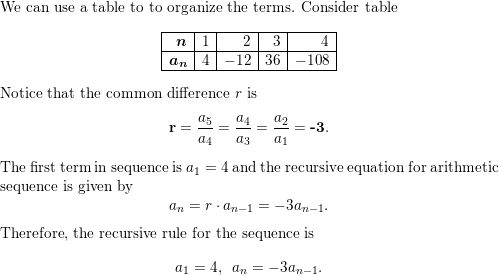
Question 15.
44, 11, \(\frac{11}{4}\), \(\frac{11}{16}\), \(\frac{11}{64}\), . . .
Answer:

Question 16.
1, 8, 15, 22, 29, . . .
Answer:
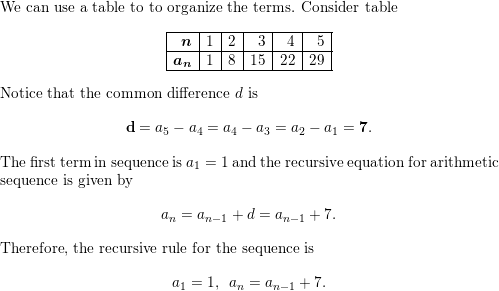
Question 17.
2, 5, 10, 50, 500, . . .
Answer:

Question 18.
3, 5, 15, 75, 1125, . . .
Answer:

Question 19.
1, 4, 5, 9, 14, . . .
Answer:

Question 20.
16, 9, 7, 2, 5, . . .
Answer:

Question 21.
6, 12, 36, 144, 720, . . .
Answer:
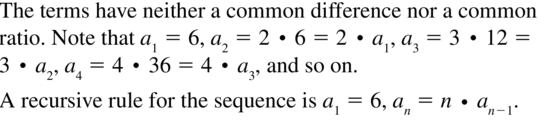
Question 22.
−3, −1, 2, 6, 11, . . .
Answer:

In Exercises 23–26, write a recursive rule for the sequence shown in the graph.
Question 23.
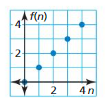
Answer:

Question 24.
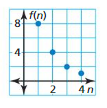
Answer:
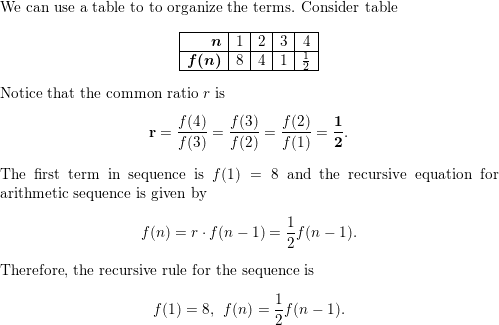
Question 25.
Answer:

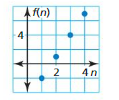
Question 26.
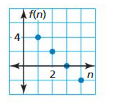
Answer:
ERROR ANALYSIS In Exercises 27 and 28, describe and correct the error in writing a recursive rule for the sequence 5, 2, 3, -1, 4, . . ..
Question 27.

Answer:
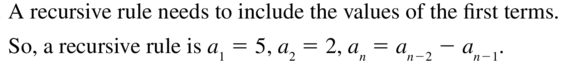
Question 28.

Answer:
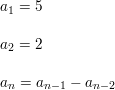
In Exercises 29–38, write a recursive rule for the sequence.
Question 29.
an = 3 + 4n
Answer:

Question 30.
an =−2 − 8n
Answer:

Question 31.
an = 12 − 10n
Answer:

Question 32.
an = 9 − 5n
Answer:

Question 33.
an = 12(11)n-1
Answer:

Question 34.
an = −7(6)n-1
Answer:
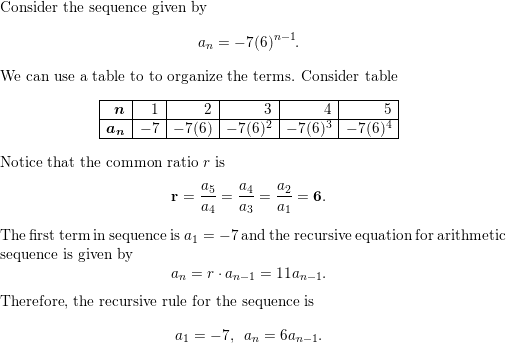
Question 35.
an = 2.5 − 0.6n
Answer:

Question 36.
an = −1.4 + 0.5n
Answer:

Question 37.
an= −\(\frac{1}{2}\left(\frac{1}{4}\right)^{n-1}\)
Answer:

Question 38.
an = \(\frac{1}{4}\)(5)n-1
Answer:
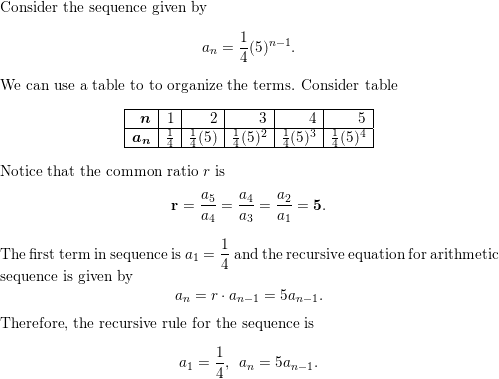
Question 39.
REWRITING A FORMULA
You have saved $82 to buy a bicycle. You save an additional $30 each month. The explicit rule an= 30n+ 82 gives the amount saved after n months. Write are cursive rule for the amount you have saved n months from now.

Answer:

Question 40.
REWRITING A FORMULA
Your salary is given by the explicit rule an = 35,000(1.04)n-1, where n is the number of years you have worked. Write a recursive rule for your salary.
Answer:

In Exercises 41–48, write an explicit rule for the sequence.
Question 41.
a1 = 3, an = an-1 − 6
Answer:

Question 42.
a1 = 16, an = an-1 + 7
Answer:
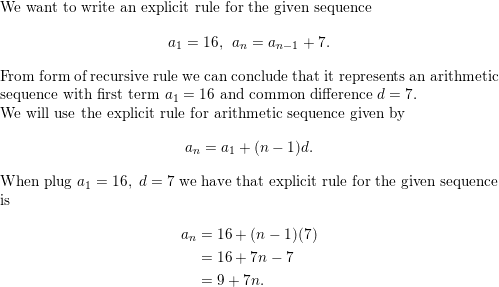
Question 43.
a1 = −2, an = 3an-1
Answer:

Question 44.
a1 = 13, an = 4an-1
Answer:
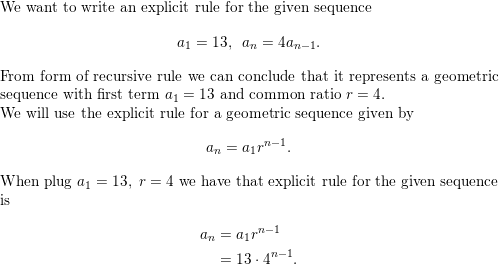
Question 45.
a1 = −12, an = an-1 + 9.1
Answer:

Question 46.
a1 = −4, an = 0.65an-1
Answer:
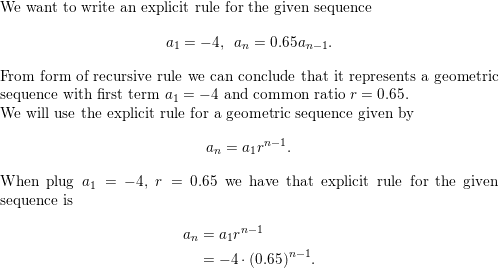
Question 47.
an = 5, an = an-1 − \(\frac{1}{3}\)
Answer:

Question 48.
a1 = −5, an = \(\frac{1}{4}\)an-1
Answer:
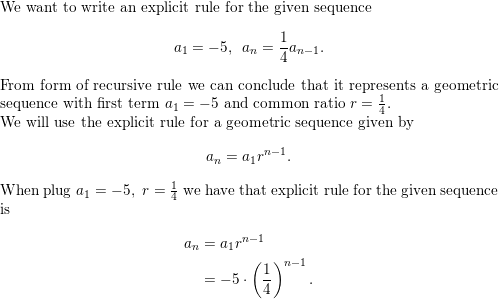
Question 49.
REWRITING A FORMULA
A grocery store arranges cans in a pyramid-shaped display with 20 cans in the bottom row and two fewer cans in each subsequent row going up. The number of cans in each row is represented by the recursive rule a1 = 20, an = an-1 − 2. Write an explicit rule for the number of cans in row n.
Answer:

Question 50.
REWRITING A FORMULA
The value of a car is given by the recursive rule a1 = 25,600, an = 0.86an-1, where n is the number of years since the car was new. Write an explicit rule for the value of the car after n years.
Answer:

Question 51.
USING STRUCTURE
What is the 1000th term of the sequence whose first term is a1 = 4 and whose nth term is an = an-1 + 6? Justify your answer.
A. 4006
B. 5998
C. 1010
D. 10,000
Answer:

Question 52.
USING STRUCTURE
What is the 873rd term of the sequence whose first term is a1 = 0.01 and whose nth term is an = 1.01an-1? Justify your answer.
A. 58.65
B. 8.73
C. 1.08
D. 586,459.38
Answer:

Question 53.
PROBLEM SOLVING
An online music service initially has 50,000 members. Each year, the company loses 20% of its current members and gains 5000 new members.
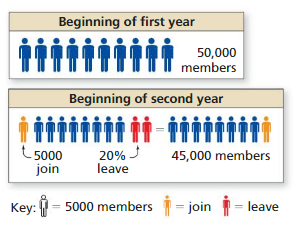
a. Write a recursive rule for the number an of members at the start of the nth year.
b. Find the number of members at the start of the fifth year.
c. Describe what happens to the number of members over time.
Answer:

Question 54.
PROBLEM SOLVING
You add chlorine to a swimming pool. You add 34 ounces of chlorine the first week and 16 ounces every week thereafter. Each week, 40% of the chlorine in the pool evaporates.
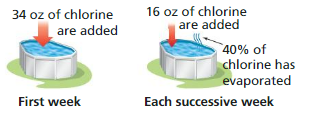
a. Write a recursive rule for the amount of chlorine in the pool at the start of the nth week.
b. Find the amount of chlorine in the pool at the start of the third week.
c. Describe what happens to the amount of chlorine in the pool over time.
Answer:
a. You add 34 ounces of chlorine the first week and 16 ounces every week thereafter. Each week, 40% of the chlorine in the pool evaporates.
an = an-1 + d
an = r . an-1
an = 0.6 × an-1 + 16
an = 0.6 × an-1 + 16
a1 = 34
b.
Enter 340
a3 = 16
Thus the amount of chlorine in the pool at the start of the third week is 16 ounces.
c.
You add 34 ounces of chlorine the first week and 16 ounces every week thereafter. Each week, 40% of the chlorine in the pool evaporates.
an = an-1 + d
an = r . an-1
an = 1333
Thus the amount of chlorine in the pool over time is 1333.
Question 55.
OPEN-ENDED
Give an example of a real-life situation which you can represent with a recursive rule that does not approach a limit. Write a recursive rule that represents the situation.
Answer:
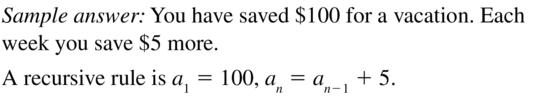
Question 56.
OPEN-ENDED
Give an example of a sequence in which each term after the third term is a function of the three terms preceding it. Write a recursive rule for the sequence and find its first eight terms.
Answer:
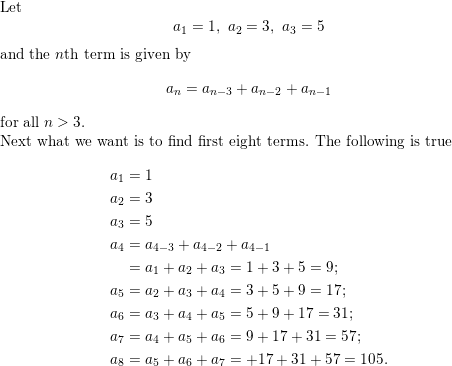
Question 57.
MODELING WITH MATHEMATICS
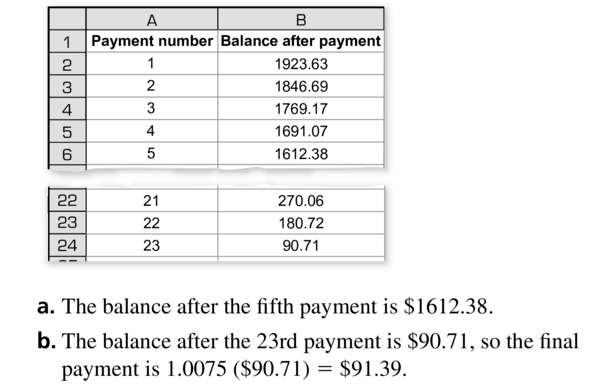
You borrow $2000 at 9% annual interest compounded monthly for 2 years. The monthly payment is $91.37.
a. Find the balance after the fifth payment.
b. Find the amount of the last payment.
Answer:

Question 58.
MODELING WITH MATHEMATICS
You borrow $10,000 to build an extra bedroom onto your house. The loan is secured for 7 years at an annual interest rate of 11.5%. The monthly payment is $173.86.
a. Find the balance after the fourth payment.
b. Find the amount of the last payment.
Answer:
Given,
You borrow $10,000 to build an extra bedroom onto your house.
The loan is secured for 7 years at an annual interest rate of 11.5%.
The monthly payment is $173.86.
0.115/12 = 0.0096
an = 1.0096 an-1
an-1 is the balance before payment
| Payment Number | Balance after payment |
| 1 | 9922.14 |
| 2 | 9843.53 |
| 3 | 9764.17 |
| . | . |
| . | . |
| . | . |
| 83 | 186.3 |
| 84 | 14.23 |
| 85 | -159.49 |
So that balance after the 4th payment will be = $9684.05
and balance after 85 payment is 173.86 – 159.49 = 14.37
Question 59.
COMPARING METHODS
In 1202, the mathematician Leonardo Fibonacci wrote Liber Abaci, in which he proposed the following rabbit problem:
Begin with a pair of newborn rabbits. When a pair of rabbits is two months old, the rabbits begin producing a new pair of rabbits each month. Assume none of the rabbits die.
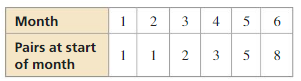
This problem produces a sequence called the Fibonacci sequence, which has both a recursive formula and an explicit formula as follows.
Recursive: a1 = 1, a2 = 1, an = an-2 + an-1
Explicit: fn = \(\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^{n}\), n ≥ 1
Use each formula to determine how many rabbits there will be after one year. Justify your answers.
Answer:

Question 60.
USING TOOLS
A town library initially has 54,000 books in its collection. Each year, 2% of the books are lost or discarded. The library can afford to purchase 1150 new books each year.
a. Write a recursive rule for the number an of books in the library at the beginning of the nth year.
b. Use the sequence mode and the dot mode of a graphing calculator to graph the sequence. What happens to the number of books in the library over time? Explain.
Answer:
a. Given,
A town library initially has 54,000 books in its collection. Each year, 2% of the books are lost or discarded. The library can afford to purchase 1150 new books each year.
an = (an-1 × 0.98) + 1150
b. The number of items increases until it stabilizes at 57,500.
At this point, the increase and decrease are equal.
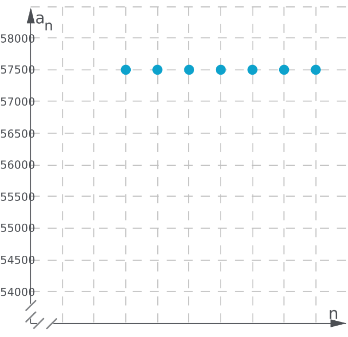
Question 61.
DRAWING CONCLUSIONS
A tree farm initially has 9000 trees. Each year, 10% of the trees are harvested and 800 seedlings are planted.
a. Write a recursive rule for the number of trees on the tree farm at the beginning of the nth year.
b. What happens to the number of trees after an extended period of time?

Answer:

Question 62.
DRAWING CONCLUSIONS
You sprain your ankle and your doctor prescribes 325 milligrams of an anti-in ammatory drug every 8 hours for 10 days. Sixty percent of the drug is removed from the bloodstream every 8 hours.
a. Write a recursive rule for the amount of the drug in the bloodstream after n doses.
Answer:
Given,
You sprain your ankle and your doctor prescribes 325 milligrams of an anti-in ammatory drug every 8 hours for 10 days. Sixty percent of the drug is removed from the bloodstream every 8 hours.
an = 0.4 an-1 + 325
a1 = 325
b. The value that a drug level approaches after an extended period of time is called the maintenance level. What is the maintenance level of this drug given the prescribed dosage?
Answer:
A doctor prescribes 325 milligram of an anti-inflammatory drug every 8 hours for 10 days and 60% of the drug is removed from the bloodstream in every 8 hours.
Substitute n = 30 in the above recursive rule and simplify to get the final answer.
a30 = 541.66
c. How does doubling the dosage affect the maintenance level of the drug? Justify your answer.
Answer:
an = 0.4 an-1 + 650 for n > 1
It is seen that after n = 12, the same value of 1083.33 is repeating. This implies that the maintenance level is 1083.33
Also, the maintenance level is 1083.33
Since 1083.33/541.6 ≈ 2, the maintenance level doubles when the dose is doubled.
Question 63.
FINDING A PATTERN
A fractal tree starts with a single branch (the trunk). At each stage, each new branch from the previous stage grows two more branches, as shown.
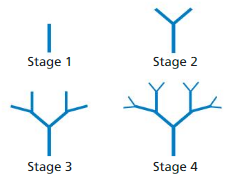
a. List the number of new branches in each of the first seven stages. What type of sequence do these numbers form?
b. Write an explicit rule and a recursive rule for the sequence in part (a).
Answer:

Question 64.
THOUGHT PROVOKING
Let a1 = 34. Then write the terms of the sequence until you discover a pattern.
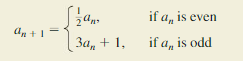
Do the same for a1 = 25. What can you conclude?
Answer:
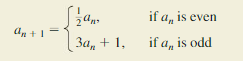
a1 = 34
a1 = 25
an+ 1 = 1/2 an
a1 = 34
a 1+1 = 1/2a1
a2 = 1/2 × 34 = 17
a3 = 1/2 × 17 = 8.5
a4 = 1/2 × 8.5 = 4.25
a5 = 1/2 × 4.25 = 2.125
a6 = 1/2 × 2.125 = 1.0625
a7 = 1/2 × 1.625 = 0.53125
a8 = 1/2 × 0.53125 = 0.265625
an+1 = 3an + 1
a1 = 25
a2 = 3a1 + 1
a2 = 3 × 25 + 1 = 76
a3 = 3 × 76 + 1 = 229
a4 = 3 × 229 + 1 = 688
a5 = 3 × 688 + 1 = 2065
a6 = 3 × 2065 + 1 = 6196
Question 65.
MODELING WITH MATHEMATICS
You make a $500 down payment on a $3500 diamond ring. You borrow the remaining balance at 10% annual interest compounded monthly. The monthly payment is $213.59. How long does it take to pay back the loan? What is the amount of the last payment? Justify your answers.
Answer:

Question 66.
HOW DO YOU SEE IT?
The graph shows the first six terms of the sequence a1 = p, an = ran-1.
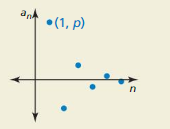
a. Describe what happens to the values in the sequence as n increases.
b. Describe the set of possible values for r. Explain your reasoning.
Answer:
Question 67.
REASONING
The rule for a recursive sequence is as follows.
f(1) = 3, f(2) = 10
f(n) = 4 + 2f(n − 1) −f (n − 2)
a. Write the first five terms of the sequence.
b. Use finite differences to find a pattern. What type of relationship do the terms of the sequence show?
c. Write an explicit rule for the sequence.
Answer:

Question 68.
MAKING AN ARGUMENT
Your friend says it is impossible to write a recursive rule for a sequence that is neither arithmetic nor geometric. Is your friend correct? Justify your answer.
Answer:
Question 69.
CRITICAL THINKING
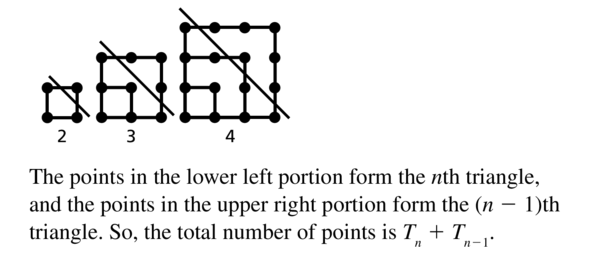
The first four triangular numbers Tn and the first four square numbers Sn are represented by the points in each diagram.
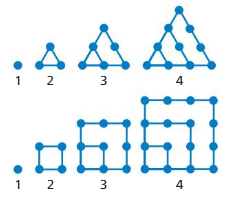
a. Write an explicit rule for each sequence.
b. Write a recursive rule for each sequence.
c. Write a rule for the square numbers in terms of the triangular numbers. Draw diagrams to explain why this rule is true.
Answer:

Question 70.
CRITICAL THINKING
You are saving money for retirement. You plan to withdraw $30,000 at the beginning of each year for 20 years after you retire. Based on the type of investment you are making, you can expect to earn an annual return of 8% on your savings after you retire.
a. Let an be your balance n years after retiring. Write a recursive equation that shows how an is related to an-1.
b. Solve the equation from part (a) for an-1. Find a0, the minimum amount of money you should have in your account when you retire. (Hint: Let a20 = 0.)
Answer:
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 71.
\(\sqrt{x}\) + 2 = 7
Answer:

Question 72.
2\(\sqrt{52}\) − 5 = 15
Answer:
2\(\sqrt{52}\) − 5 = 15
Squaring on both sides
4 × 52 – 25 = 15
208 – 25 = 15
183 ≠ 15
Question 73.
\(\sqrt [ 3 ]{ x }\) + 16 = 19
Answer:

Question 74.
2\(\sqrt [ 3 ]{ x }\) − 13 = −5
Answer:
2\(\sqrt [ 3 ]{ x }\) − 13 = −5
Cubing on both sides
8 × x – 2197 = -125
8x = 2197 – 125
8x = 2072
x = 259
The variables x and y vary inversely. Use the given values to write an equation relating x and y. Then find y when x = 4.
Question 75.
x = 2, y = 9
Answer:
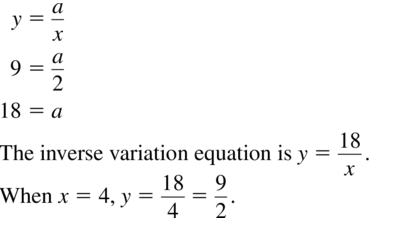
Question 76.
x =−4, y = 3
Answer:
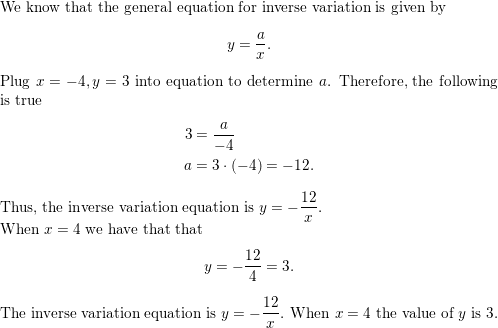
Question 77.
x = 10, y = 32
Answer:
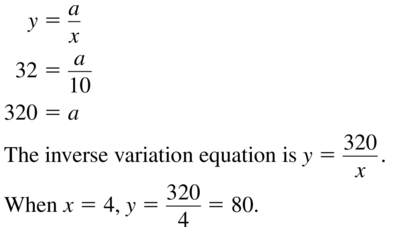
Sequences and Series Performance Task: Integrated Circuits and Moore s Law
8.4–8.5What Did You Learn?
Core Vocabulary
partial sum, p. 436
explicit rule, p. 442
recursive rule, p. 442
Core Concepts
Section 8.4
Partial Sums of Infinite Geometric Series, p. 436
The Sum of an Infinite Geometric Series, p. 437
Section 8.5
Evaluating Recursive Rules, p. 442
Recursive Equations for Arithmetic and Geometric Sequences, p. 442
Translating Between Recursive and Explicit Rules, p. 444
Mathematical Practices
Question 1.
Describe how labeling the axes in Exercises 3–6 on page 439 clarifies the relationship between the quantities in the problems.
Answer:
Question 2.
What logical progression of arguments can you use to determine whether the statement in Exercise 30 on page 440 is true?
Answer:
Question 3.
Describe how the structure of the equation presented in Exercise 40 on page 448 allows you to determine the starting salary and the raise you receive each year.
Answer:
Question 4.
Does the recursive rule in Exercise 61 on page 449 make sense when n= 5? Explain your reasoning.
Answer:
Performance Task: Integrated Circuits and Moore s Law
In April of 1965, an engineer named Gordon Moore noticed how quickly the size of electronics was shrinking. He predicted how the number of transistors that could fit on a 1-inch diameter circuit would increase over time. In 1965, only 50 transistors fit on the circuit. A decade later, about 65,000 transistors could fit on the circuit. Moore’s prediction was accurate and is now known as Moore’s Law. What was his prediction? How many transistors will be able to fit on a 1-inch circuit when you graduate from high school?
To explore the answers to this question and more, go to BigIdeasMath.com.

Sequences and Series Chapter Review
8.1 Defining and Using Sequences and Series (pp. 409–416)
Question 1.
Describe the pattern shown in the figure. Then write a rule for the nth layer of the figure, where n = 1 represents the top layer.
Answer:

Write the series using summation notation.
Question 2.
7 + 10 + 13 +. . .+ 40
Answer:
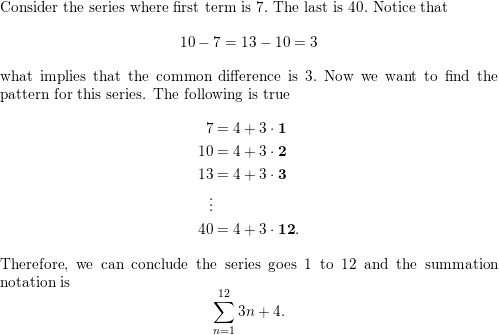
Question 3.
0 + 2 + 6 + 12 +. . . .
Answer:
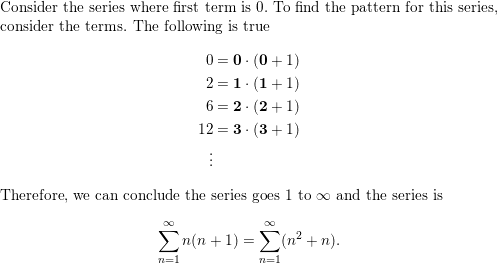
Find the sum
Question 4.
\(\sum_{i=2}^{7}\)(9 – i3)
Answer:
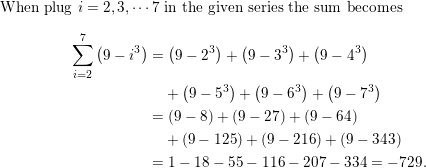
Question 5.
\(\sum_{i=1}^{46}\)i
Answer:
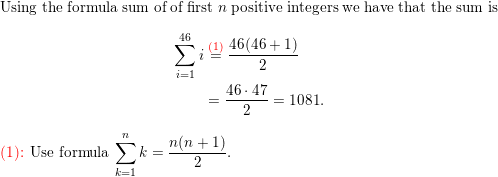
Question 6.
\(\sum_{i=1}^{12}\)i2
Answer:
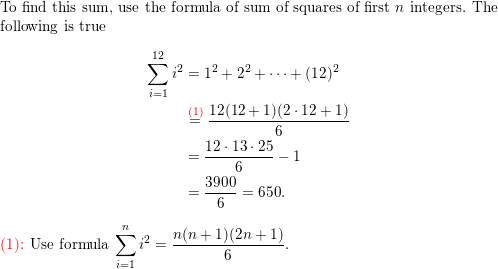
Question 7.
\(\sum_{i=1}^{5} \frac{3+i}{2}\)
Answer:
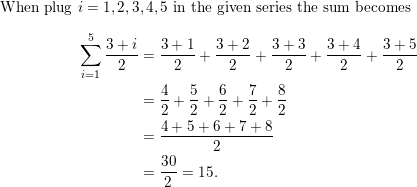
8.2 Analyzing Arithmetic Sequences and Series (pp. 417–424)
Question 8.
Tell whether the sequence 12, 4, −4, −12, −20, . . . is arithmetic. Explain your reasoning.
Answer:
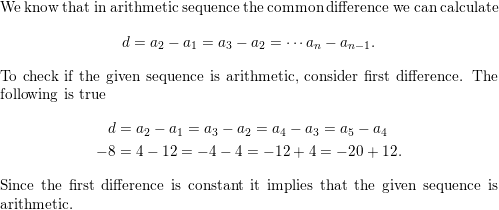
Write a rule for the nth term of the arithmetic sequence. Then graph the first six terms of the sequence.
Question 9.
2, 8, 14, 20, . . .
Answer:
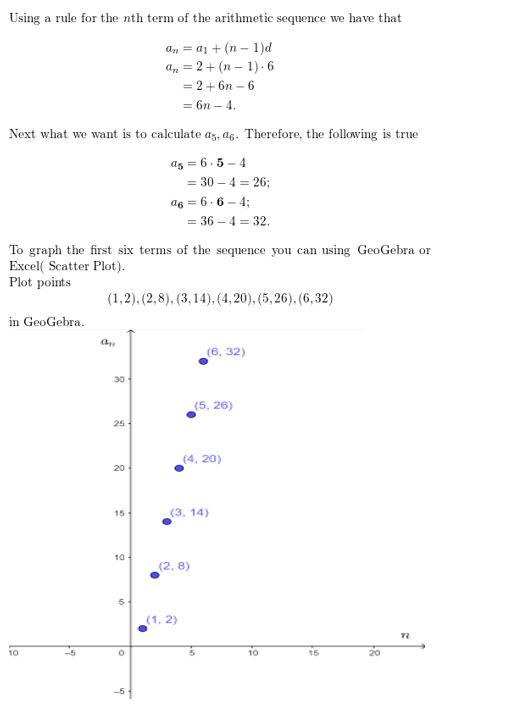
Question 10.
a14 = 42, d = 3
Answer:

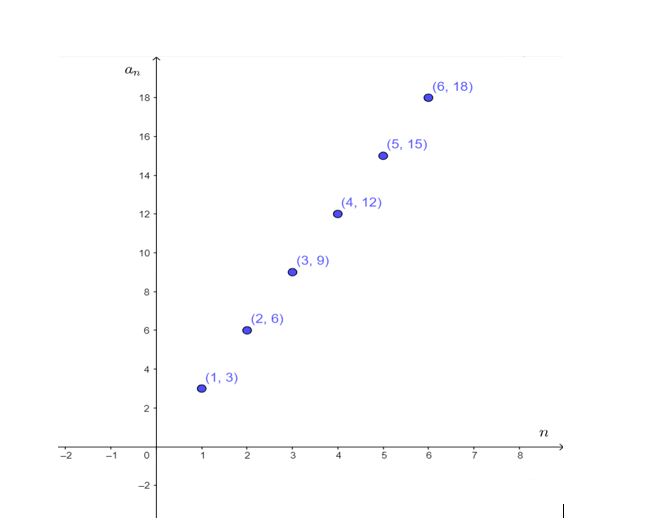
Question 11.
a6 = −12, a12 = −36
Answer:
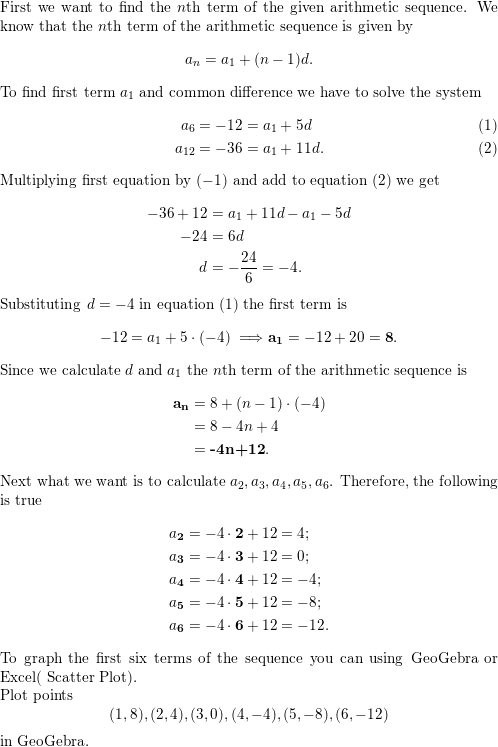
Question 12.
Find the sum \(\sum_{i=1}^{36}\)(2 + 3i) .
Answer:
Question 13.
You take a job with a starting salary of $37,000. Your employer offers you an annual raise of $1500 for the next 6 years. Write a rule for your salary in the nth year. What are your total earnings in 6 years?
Answer:
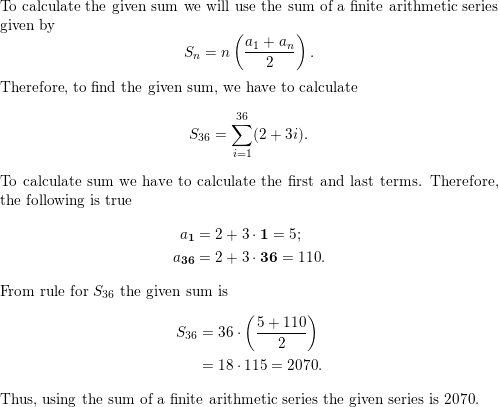
8.3 Analyzing Geometric Sequences and Series (pp. 425–432)
Question 14.
Tell whether the sequence 7, 14, 28, 56, 112, . . . is geometric. Explain your reasoning.
Answer:
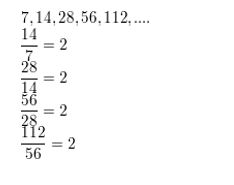
Write a rule for the nth term of the geometric sequence. Then graph the first six terms of the sequence.
Question 15.
25, 10, 4, \(\frac{8}{5}\) , . . .
Answer:
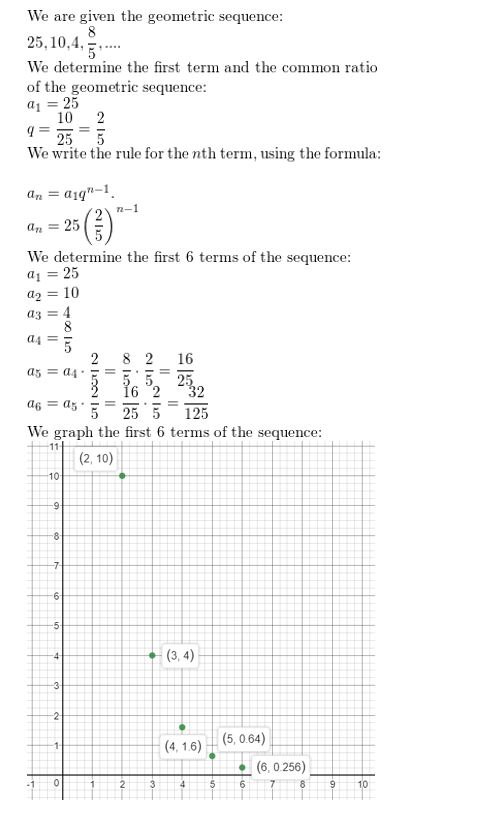
Question 16.
a5 = 162, r =−3
Answer:
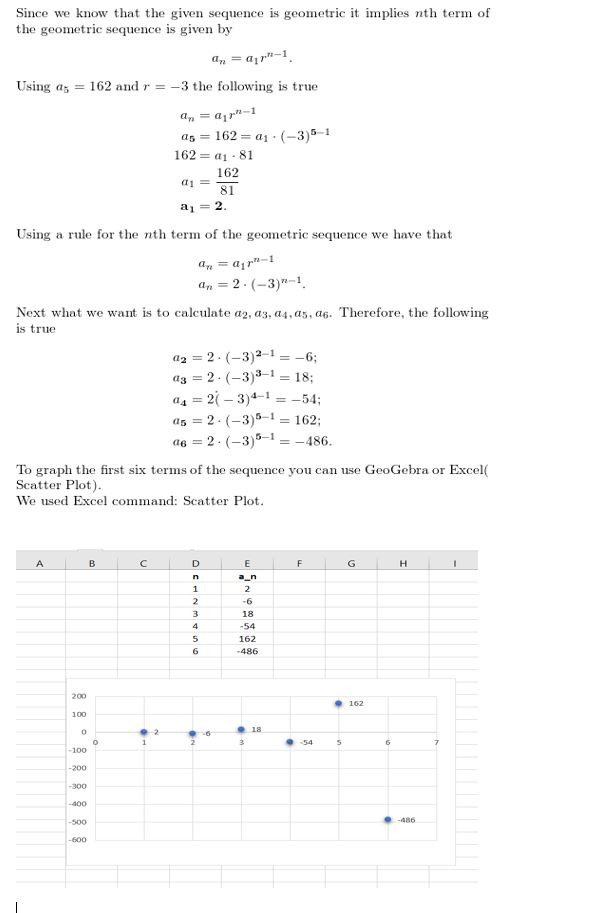
Question 17.
a3 = 16, a5 = 256
Answer:

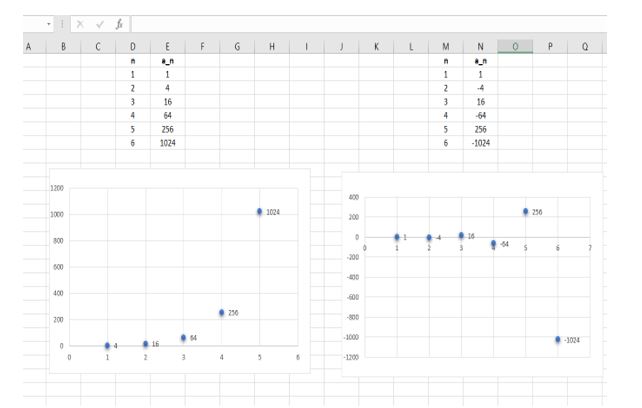
Question 18.
Find the sum \(\sum_{i=1}^{9}\)5(−2)i−1 .
Answer:
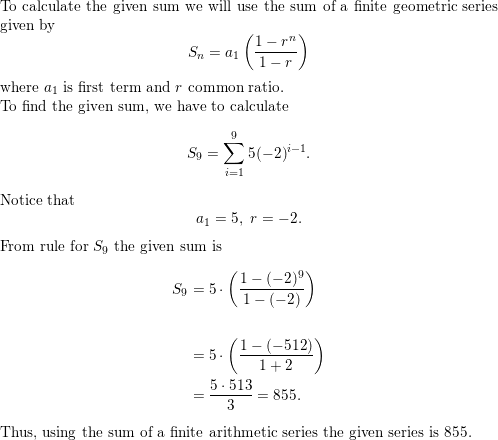
8.4 Finding Sums of Infinite Geometric Series (pp. 435–440)
Question 19.
Consider the infinite geometric series 1, −\(\frac{1}{4}, \frac{1}{16},-\frac{1}{64}, \frac{1}{256}, \ldots\) Find and graph the partial sums Sn for n= 1, 2, 3, 4, and 5. Then describe what happens to Sn as n increases.
Answer:

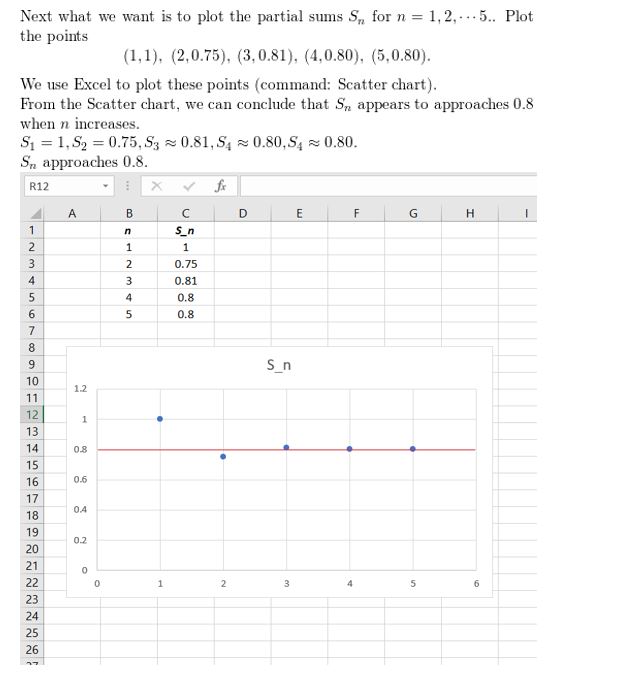
Question 20.
Find the sum of the infinite geometric series −2 + \(\frac{1}{2}-\frac{1}{8}+\frac{1}{32}+\cdots\), if it exists.
Answer:
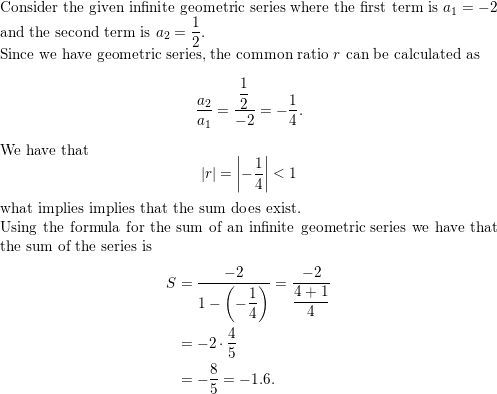
Question 21.
Write the repeating decimal 0.1212 . . . as a fraction in simplest form.
Answer:

8.5 Using Recursive Rules with Sequences (pp. 441–450)
Write the first six terms of the sequence.
Question 22.
a1 = 7, an = an-1 + 11
Answer:
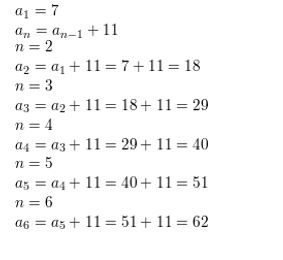
Question 23.
a1 = 6, an = 4an-1
Answer:
Given that
a1 = 6, an = 4an-1
If n= 2.
a2 = 4a2-1
a2 = 4a1
a2 = 4(6) = 24.
a3 = 4(24) = 96
a4 = 4(96) = 384
a5 = 4(384) =1,536
a6 = 4( 1,536) = 6,144
Question 24.
f(0) = 4, f(n) = f(n − 1) + 2n
Answer:
Given that,
f(0) = 4 and f(n) = f(n-1) + 2n
If n = 1.
f(1) = f(1-1) + 2(1)
= f(0) + 2 = 4 + 1 = 5
n = 2
f(2) = f(2-1) + 2(2) = 5 + 4
f(2) = 9.
n = 3
f(3) = f(3-1) + 2(3)
f(3) = f(2) + 6 = 9 + 6
f(3) = 15.
f(4) = f(4-1) + 2(4)
f(4) = f(3) + 8 = 15 + 8
f(4) = 23.
f(5) = f(5-1) + 2(5) = f(4) + 10
= 23 + 10
f(5) = 33.
f(6) = f(6-1) + 2(6) = f(5) + 12
= 33 + 12
f(6) = 45
Write a recursive rule for the sequence.
Question 25.
9, 6, 4, \(\frac{8}{3}\), \(\frac{16}{9}\), . . .
Answer:
Question 26.
2, 2, 4, 12, 48, . . .
Answer:
Given that the sequence is 2, 2, 4, 12, 48.
First, assume that,
a1 = 2,
a2 = 2 = 1 x 2 = 1 x a1.
a3 = 4 = 2 x 2 = 2 x a2.
a4 = 12 = 3 x 4 = 3 x a3.
a5 = 48 = 4 x 12 = 4 x a4.
We can conclude that
an = (n-1) x an-1
The recursive rule for the sequence is a1 = 2, an = (n-1) x an-1.
Question 27.
7, 3, 4, −1, 5, . . .
Answer:
Given that the sequence is 7, 3, 4, -1, 5.
Here a1 = 7, a2 = 3, a3 = 4, a5 = -1, a6 = 5.
Therefore, the recursive rule for the sequence is an = an-2 – an-1.
Question 28.
Write a recursive rule for an = 105 (\(\frac{3}{5}\))n−1 .
Answer:
Given that,
an = 105(3/5)n−1 .
Compare the given equation with the nth term
an = a1 x rn−1 ..
The value of a1 is 105 and the constant ratio r = 3/5.
Substitute r in the above equation.
an = r x an−1 .
an = 3/5 x an−1 .
Hence the recursive equation is an = 3/5 x an−1 .
Write an explicit rule for the sequence.
Question 29.
a1 = −4, an = an-1 + 26
Answer:
Given that,
a1 = -4, an = an-1 + 26.
Let us consider n = 2.
a2 = a2-1 + 26 = a1 + 26 = -4 + 26 = 22.
a3 = a3-1 + 26 = a2 + 26 = 22 + 26 = 48.
a4 = a4-1 + 26 = a3 + 26 = 48 + 26 = 74.
a5 = a5-1 + 26 = a4 + 26 = 74 + 26 = 100.
a6 = a6-1 + 26 = a5 + 26 = 100 + 26 = 126.
Question 30.
a1 = 8, an = −5an-1
Answer:
Given that,
a1 = 8, an = -5an-1.
Let us consider n = 2.
a2 = -5(a2-1) = -5a1 = -5(8) = 40.
a3 = -5(a3-1) = -5a2 = -5(40) = -200.
a4 = -5(a4-1) = -5a3 = -5(-200) = 1000.
a5 = -5(a5-1) = -5a4 = -5(1000) = -5000.
a6 = -5(a6-1) = -5a5 = -5(-5000) = 25,000.
Question 31.
a1 = 26, an = \(\frac{2}{5}\)an-1.
Answer:
Given that,
a1 = 26, an = 2/5 (an-1)
Let us consider n = 2
a2 = 2/5 (a2-1) = 2/5 (a1) = 2/5 x 26 = 10.4
a3 = 2/5 (a3-1) = 2/5 (a2) = 2/5 x 10.4 = 4.16
a4 = 2/5 (a4-1) = 2/5 (a3) = 2/5 x 4.16 = 1.664
a5 = 2/5 (a5-1) = 2/5 (a4) = 2/5 x 1.664 = 0.6656
a6 = 2/5 (a6-1) = 2/5 (a5) = 2/5 x 0.6656 = 0.26624.
Question 32.
A town’s population increases at a rate of about 4% per year. In 2010, the town had a population of 11,120. Write a recursive rule for the population Pn of the town in year n. Let n = 1 represent 2010.
Answer:
Question 33.
The numbers 1, 6, 15, 28, . . . are called hexagonal numbers because they represent the number of dots used to make hexagons, as shown. Write a recursive rule for the nth hexagonal number.
Answer:
Sequences and Series Chapter Test
Find the sum.
Question 1.
\(\sum_{i=1}^{24}\)(6i− 13)
Answer:
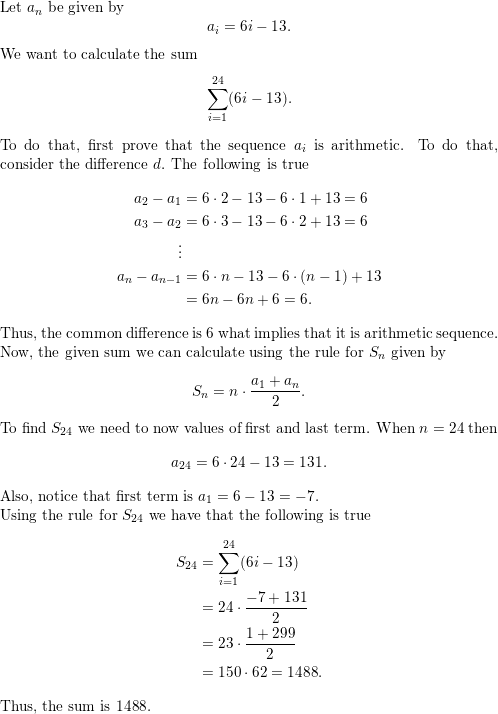
Question 2.
\(\sum_{n=1}^{16}\)n2
Answer:

Question 3.
\(\sum_{k=1}^{\infty}\)2(0.8)k−1
Answer:
Question 4.
\(\sum_{i=1}^{6}\)4(−3)i−1
Answer:
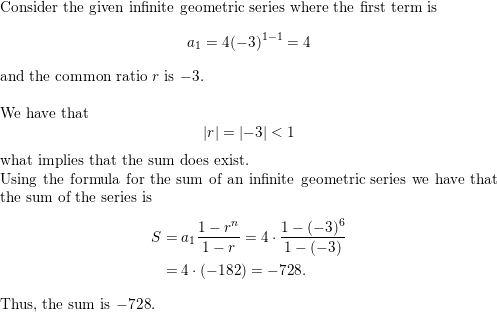
Determine whether the graph represents an arithmetic sequence, geometric sequence, or neither. Explain your reasoning. Then write a rule for the nth term.
Question 5.
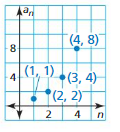
Answer:
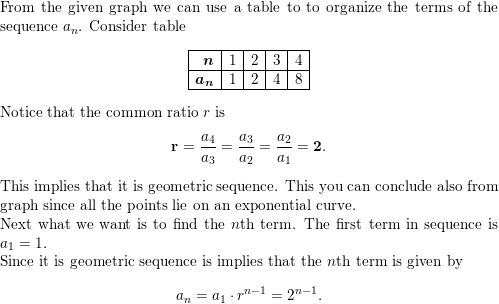
Question 6.
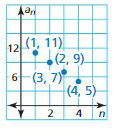
Answer:

Question 7.
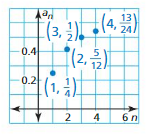
Answer:

Write a recursive rule for the sequence. Then find a9.
Question 8.
a1 = 32, r = \(\frac{1}{2}\)
Answer:
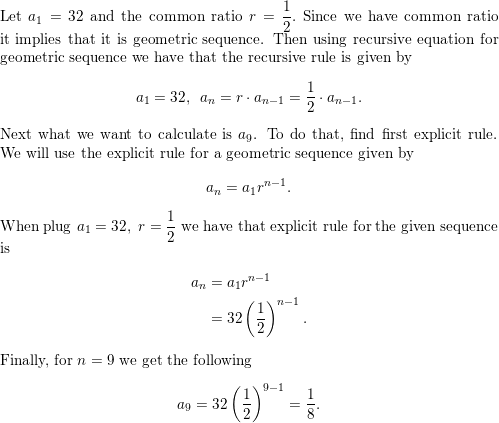
Question 9.
an = 2 + 7n
Answer:
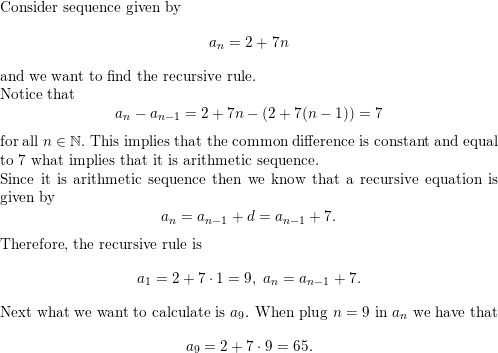
Question 10.
2, 0, −3, −7, −12, . . .
Answer:
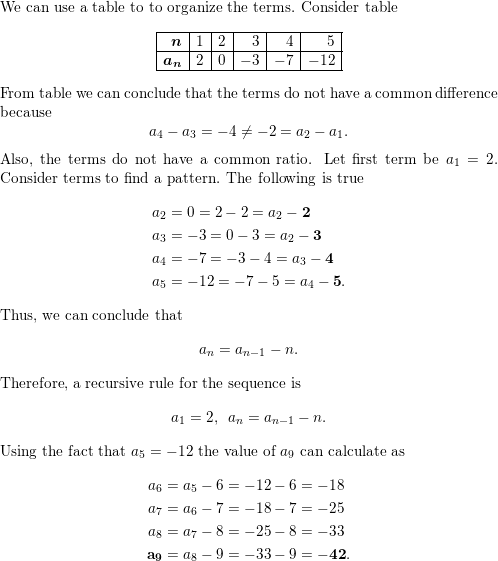
Question 11.
Write a recursive rule for the sequence 5, −20, 80, −320, 1280, . . .. Then write an explicit rule for the sequence using your recursive rule.
Answer:

Question 12.
The numbers a, b, and c are the first three terms of an arithmetic sequence. Is b half of the sum of a and c? Explain your reasoning.
Answer:
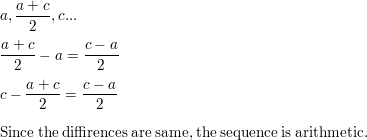
Question 13.
Use the pattern of checkerboard quilts shown.
a. What does n represent for each quilt? What does an represent?
b. Make a table that shows n and an for n= 1, 2, 3, 4, 5, 6, 7, and 8.
c. Use the rule an = \(\frac{n^{2}}{2}+\frac{1}{4}\)[1 − (−1)n] to find an for n = 1, 2, 3, 4, 5, 6, 7, and 8.
Compare these values to those in your table in part (b). What can you conclude? Explain.
Answer:

Question 14.
During a baseball season, a company pledges to donate $5000 to a charity plus $100 for each home run hit by the local team. Does this situation represent a sequence or a series? Explain your reasoning.
Answer:
Question 15.
The lengthℓ1 of the first loop of a spring is 16 inches. The lengthℓ2 of the second loop is 0.9 times the length of the first loop. The lengthℓ3 of the third loop is 0.9 times the length of the second loop, and so on. Suppose the spring has infinitely many loops, would its length be finite or infinite? Explain. Find the length of the spring, if possible.
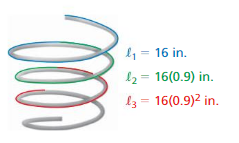
Answer:
Sequences and Series Cumulative Assessment
Question 1.
The frequencies (in hertz) of the notes on a piano form a geometric sequence. The frequencies of G (labeled 8) and A (labeled 10) are shown in the diagram. What is the approximate frequency of E at (labeled 4)?
Answer:
Question 2.
You take out a loan for $16,000 with an interest rate of 0.75% per month. At the end of each month, you make a payment of $300.
a. Write a recursive rule for the balance an of the loan at the beginning of the nth month.
b. How much do you owe at the beginning of the 18th month?
c. How long will it take to pay off the loan?
d. If you pay $350 instead of $300 each month, how long will it take to pay off the loan? How much money will you save? Explain.
Answer:
Question 3.
The table shows that the force F (in pounds) needed to loosen a certain bolt with a wrench depends on the length ℓ (in inches) of the wrench’s handle. Write an equation that relates ℓ and F. Describe the relationship.
Answer:
Question 4.
Order the functions from the least average rate of change to the greatest average rate of change on the interval 1 ≤ x ≤ 4. Justify your answers.
Answer:
Question 5.
A running track is shaped like a rectangle with two semicircular ends, as shown. The track has 8 lanes that are each 1.22 meters wide. The lanes are numbered from 1 to 8 starting from the inside lane. The distance from the center of a semicircle to the inside of a lane is called the curve radius of that lane. The curve radius of lane 1 is 36.5 meters, as shown in the figure.
a. Is the sequence formed by the curve radii arithmetic, geometric, or neither? Explain.
b. Write a rule for the sequence formed by the curve radii.
c. World records must be set on tracks that have a curve radius of at most 50 meters in the outside lane. Does the track shown meet the requirement? Explain.
Answer:
Question 6.
The diagram shows the bounce heights of a basketball and a baseball dropped from a height of 10 feet. On each bounce, the basketball bounces to 36% of its previous height, and the baseball bounces to 30% of its previous height. About how much greater is the total distance traveled by the basketball than the total distance traveled by the baseball?
A. 1.34 feet
B. 2.00 feet
C. 2.68 feet
D. 5.63 feet
Answer:
Question 7.
Classify the solution(s) of each equation as real numbers, imaginary numbers, or pure imaginary numbers. Justify your answers.
a. x + \(\sqrt{-16}\) = 0
b. (11 – 2i) – (-3i + 6) = 8 + x
c. 3x2 – 14 = -20
d. x2 + 2x = -3
e. x2 = 16
f. x2 – 5x – 8 = 0
Answer:
