Big Ideas Math Algebra 1 Answers Chapter 2 Solving Linear Inequalities

Wondering how to clear your doubts regarding the BIM Algebra 1 Chapter 2 Solving Linear Inequalities? Then you have come the right way and we will help you by providing the Big Ideas Math Algebra 1 Answer Key Chapter 2 Solving Linear Inequalities given by subject experts. Avail them during your preparation and understand the concepts of Big Ideas Math Algebra 1 Answers easily.

You will find solutions to all the Big Ideas Math Chapter 2 Solving Linear Inequalities Exercises 2.1 to 2.6, along with Chapter Test, Review Tests, Cumulative Practice, Quiz, etc. Make the most out of this preparation material and stand out from the crowd and score better grades in your exams.

Big Ideas Math Book Algebra 1 Answer Key Chapter 2 Solving Linear Inequalities

Practicing using the Big Ideas Math Algebra 1 Answer Key Ch 2 Solving Linear Inequalities and learn how to solve various questions easily. BIM Book Algebra 1 Chapter 2 Solving Linear Inequalities Solution Key will aid in your preparation and enhances your conceptual knowledge. All the Solutions prepared are given by subject experts keeping in mind the latest syllabus guidelines.

You can refer to Big Ideas Math Answers for Grades K-8 to learn all the chapters and concepts in it effectively. For the sake of your convenience, we have curated the quick links for all the Lessons and Exercises in the Big Ideas Math Book Algebra 1 Answer Key Solving Linear Inequalities. You just need to tap on them to learn about the particular concept in no time.

• Solving Linear Inequalities Maintaining Mathematical Proficiency – Page 51
• Solving Linear Inequalities Mathematical Practices – Page 52
• Lesson 2.1 Writing and Graphing Inequalities – Page(53-60)
• Writing and Graphing Inequalities 2.1 Exercises – Page(58-60)
• Lesson 2.2 Solving Inequalities Using Addition or Subtraction – Page(61-66)
• Solving Inequalities Using Addition or Subtraction 2.2 Exercises – Page(65-66)
• Lesson 2.3 Solving Inequalities Using Multiplication or Division – Page(67-72)
• Solving Inequalities Using Multiplication or Division 2.3 Exercises – Page(71-72)
• Lesson 2.4 Solving Multi-step Inequalities – Page(73-78)
• Solving Multi-step Inequalities 2.4 Exercises – Page(77-78)
• Solving Linear Inequalities Study Skills: Analyzing Your Errors – Page 79
• Solving Linear Inequalities Maintaining 2.1 – 2.4 Quiz – Page 80
• Lesson 2.5 Solving Compound Inequalities – Page(81-86)
• Solving Compound Inequalities 2.5 Exercises – Page(85-86)
• Lesson 2.6 Solving Absolute Value Inequalities – Page(87-92)
• Solving Absolute Value Inequalities 2.6 Exercises – Page(91-92)
• Solving Linear Inequalities Performance Task: Grading Calculations – Page 93
• Solving Linear Inequalities Chapter Review – Page(94-96)
• Solving Linear Inequalities Chapter Test – Page 97
• Solving Linear Inequalities Maintaining Cumulative Assessment – Page(98-99)

Solving Linear Inequalities Maintaining Mathematical Proficiency

Graph the number.

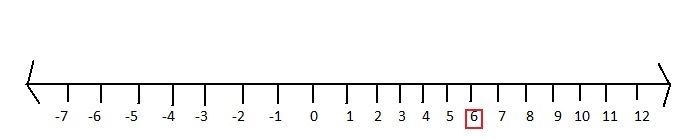
Question 1.
6
Answer:
The number line representing 6 is:

Question 2.
| 2 |
Answer:
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
The number line representing | 2 | is:

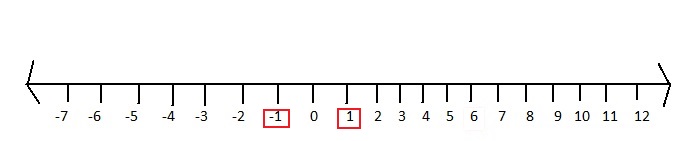
Question 3.
| -1 |
Answer:
We know that,
| -x | = x for x > 0
| -x | = -x for x < 0
So,
The number line representing | -1 | is:

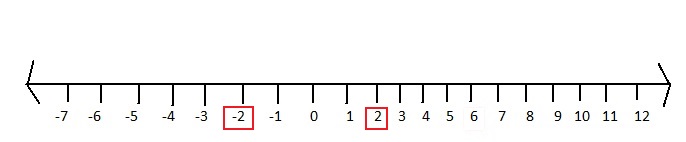
Question 4.
2 + | -2 |
Answer:
The given absolute value expression is:
2 + | -2 |
We know that,
| -x | =x for x > 0
| -x | = -x for x < 0
So,
2 + | -2 | = 2 + 2                                                 2 + | – 2 | = 2 – 2
= 4                                                                       = 0
Hence,
The number line representing the values of 2 + | – 2 | is:

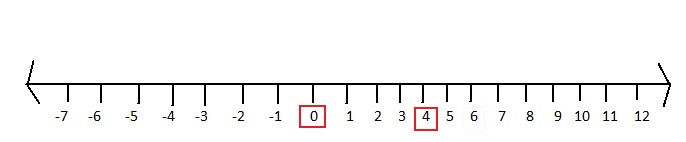
Question 5.
1 – | -4 |
Answer:
The given absolute value expression is:
1 – | – 4 |
We know that,
| -x | = x for x > 0
| – x | = -x for x < 0
So,
1 – | – 4 | = 1 – 4                                      1 – | – 4 | = 1 – ( -4 )
= -3                                                          = 5
Hence,
The number line representing the values of 1 – | – 4 | is:

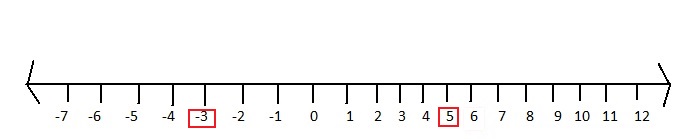
Question 6.
-5 + | 3 |
Answer:
The given absolute value expression is:
-5 + | 3 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
-5 + | 3 | = -5 + 3                                 -5 + | 3 | = -5 -3
= -2                                                        = -8
Hence,
The number line representing the values of -5 + | 3 | is:

Complete the statement with <, >, or =.

Question 7.

Answer:
We know that,
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hence, from the above,
We can conclude that
2 < 9

Question 8.

Answer:
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hence, from the above,
We can conclude that
-6 < 5

Question 9.

Answer:
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
We know that,
The greater number in the positive integers is the lesser number in the negative integers
Hence, from the above,
We can conclude that
-12 < -4

Question 10.

Answer:
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
We know that,
The greater number in the positive integers is the lesser number in the negative integers
Hence, from the above,
We can conclude that
-7 > -13

Question 11.

Answer:
We know that,
| -x | = x for x > 0
| -x | = -x for x < 0
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
We know that,
The greater number in the positive integers is the lesser number in the negative integers
Hence, from the above,
We can conclude that
8 = 8 ( or ) -8 = -8

Question 12.

Answer:
We know that,
| -x | = x for x > 0
| -x | = -x for x < 0
The order of the numbers in the ascending order is:
-9, -8, -7, -6, -5, -4 ,-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
We know that,
The greater number in the positive integers is the lesser number in the negative integers
Hence, from the above,
We can conclude that
-10 < 18    ( or ) -10 > -18

Question 13.
ABSTRACT REASONING
A number a is to the left of a number b on the number line. How do the numbers -a and -b compare?
Answer:
It is given that a number a is to the left of a number b on the number line.
So,
The representation of a and b on the number line is:

Hence, from the above number line
We can conclude that
-a > -b

Solving Linear Inequalities Mathematical Practices

Monitoring Progress

Use a graphing calculator to solve the inequality.

Question 1.
2x + 3 < x – 1
Answer:
The given inequality is:
2x + 3 < x – 1
We know that,
When we convert the mathematical symbols from LHS to RHS, the sign of that mathematical symbol change. i.e.,
+ will be converted into – and vice – versa
× will be converted into ÷ and vice-versa
So,
2x – x < -1 – 3
x < – 4
Hence,
The representation of the solved inequality in the number line is:

Question 2.
-x – 1 > -2x + 2
Answer:
The given inequality is:
-x – 1 > -2x + 2
We know that,
When we convert the mathematical symbols from LHS to RHS, the sign of that mathematical symbol change. i.e.,
+ will be converted into – and vice – versa
× will be converted into ÷ and vice-versa
So,
-x + 2x > 2 + 1
x > 3
Hence,
The representation of the solved inequality in the number line is:

Question 3.
\(\frac{1}{2}\)x + 1 > \(\frac{3}{2}\)x + 3
Answer:
The given inequality is:
\(\frac{1}{2}\)x + 1 > \(\frac{3}{2}\)x + 3
We know that,
When we convert the mathematical symbols from LHS to RHS, the sign of that mathematical symbol change. i.e.,
+ will be converted into – and vice – versa
× will be converted into ÷ and vice-versa
So,
\(\frac{1}{2}\)x – \(\frac{3}{2}\)x > 3 – 1
\(\frac{1 – 3}{2}\)x > 2
\(\frac{-2}{2}\)x > 2
\(\frac{-1}{1}\)x > 2
-x > 2
Multiply with –  both sides
So,
x > -2
Hence,
The representation of the solved inequality in the number line is:

Lesson 2.1 Writing and Graphing Inequalities

Essential Question

How can you use an inequality to describe a real-life statement?
Answer:
Inequality is just a relationship between two amounts, in which the amounts are not the same.
Example:
She completed her work before anyone else. i.e., her finish time was less than everyone else

EXPLORATION 1
Writing and Graphing Inequalities

Work with a partner. Write an inequality for each statement. Then sketch the graph of the numbers that make each inequality true.
a. Statement The temperature t in Sweden is at least -10°C.
Inequality
Graph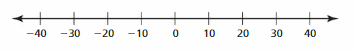
Answer:
The given graph is:

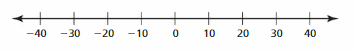
It s given that the temperature t in Sweden is at least -10°C
The meaning of the above statement is that the temperature of Sweden is -10°C or greater than -10°C
Hence,
The representation of the temperature of Sweden in the graph is:

b. Statement The elevation e of Alabama is at most 2407 feet.
Inequality
Graph
Answer:
The given graph is:

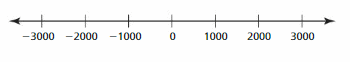
It is given that the elevation ‘ e ‘ of Alabama is at most 2,407 feet
From the given graph,
We can say that the gap between each elevation is 1,000 feet
So,
The elevation of Alabama will come between 2000 and 3000 in the number line
Hence,
The representation of the elevation of Alabama in the given graph is:

Answer:
EXPLORATION 2
Writing Inequalities
Work with a partner. Write an inequality for each graph. Then, in other words, describe all the values of x that make each inequality true.

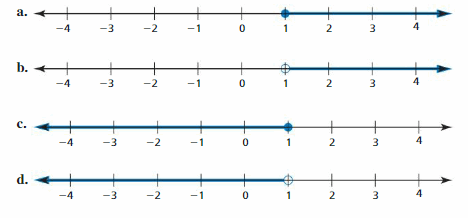
Answer:
The given number lines are:

a)
From the given number line,
The value of x marked from 1 to 4
Hence,
The inequality representing the given number line is:
x ≥ 1
b)
From the given number line,
The value of x marked after 1 till the end of the number line
Hence,
The inequality representing the given number line is:
x > 1
c)
From the given number line,
The value of x marked from 1 till the end of the left side of the number line.
Hence,
The inequality representing the given number line is:
x ≤ 1
d)
From the given number line,
The value of x marked before 1 till the end of the left side of the number line
Hence,
The inequality representing the given number lie is:
x < 1

Communicate Your Answer

Question 3.
How can you use an inequality to describe a real-life statement?
Answer:
Inequality is just a relationship between two amounts, in which the amounts are not the same.
Example:
A ball in the net is worth two in the bush. i.e., the value of a single ball in the net is greater than the value of a single ball in the bush.

Question 4.
Write a real-life statement that involves each inequality.
a. x < 3.5
b. x ≤ 6
c. x > -2
d. x ≥ 10
Answer:
a)
The given inequality is:
x < 3.5
The real-life situation that involves the given inequality is:
The number of birds that are less than the height of 3.5 inches
b)
The given inequality is:
x ≤ 6
The real- life situation that involves the given inequality is:
The number of people that are buying the mobiles from a mobile store
c)
The given inequality is:
x > -2
The real-life situation that involves the given inequality is:
The number of integers that are greater than -2
d)
The given inequality is:
x ≥ 10
The real-life situation that involves the given inequality is:
The number of chocolates that are distributed greater than or equal to 10 children

2.1 Lesson

Monitoring Progress

Write the sentence as an inequality.

Question 1.
A number b is fewer than 30.4.
Answer:
The given sentence is:
A number b is fewer than 30.4
Hence,
The representation of the given sentence in the form of inequality is:
b < 30.4

Question 2.
–\(\frac{7}{10}\) is at least twice a number k minus 4.
Answer:
The given sentence is:
–\(\frac{7}{10}\) is at least twice a number k minus 4.
Hence,
The representation of the given sentence in the form of inequality is:
–\(\frac{7}{10}\) = 2k – 4

Tell whether −6 is a solution to the inequality.

Question 3.
c + 4 < -1
Answer:
-6 is not a solution to the given inequality

Explanation:
The given equation is:
c + 4 = -1
So,
c = -4 – 1
c = -5
Hence, from the above,
We can conclude that -6 is not a solution to the given inequality

Question 4.
10 ≤ 3 – m
Answer:
-6 is not a solution to the given inequality

Explanation:
The given inequality is:
10 ≤ 3 – m
So,
-m ≤ 10 – 3
-m ≤ 7
Multiply by – on both sides
m ≤ -7
Hence, from the above,
We can conclude that -6 is not a solution to the given inequality

Question 5.
21 ÷ x ≥ -3.5
Answer:
-6 is a solution to the given inequality

Explanation:
The given inequality is:
21 ÷ x ≥ -3.5
So,
-21 ÷ 3.5 ≥ x
-210 ÷ 35 ≥ x
-6 ≥ x
x ≤ -6
Hence, from the above,
We can conclude that -6 is a solution to the given inequality

Question 6.
4x – 25 > -2
Answer:
-6 is not a solution to the given inequality

Explanation:
The given inequality is:
4x – 25 > -2
So,
4x > -2 + 25
4x > 23
x > 23 ÷ 4
x > 5.75
Hence, from the above,
We can conclude that -6 is not a solution to the given inequality

Graph the inequality.

Question 7.
b > -8
Answer:
The given inequality is:
b > -8
Hence,
The representation of the given inequality in the number line is:

Question 8.
1.4 ≥ g
Answer:
The given inequality is:
1.4 ≥ g
So,
g ≤ 1.4
Hence,
The representation of the given inequality in the number line is:

Question 9.
r < \(\frac{1}{2}\)
Answer:
The given inequality is:
r < \(\frac{1}{2}\)
So,
r < 0.5
Hence,
The representation of the given inequality in the number line is:

Question 10.
v ≥ \(\sqrt{36}\)
Answer:
The given inequality is:
v > \(\sqrt{36}\)
So,
v > 6
Hence,
The representation of the given inequality in the number line is:

Question 11.
Write an inequality that represents the graph.

Answer:
The given graph is:

From the given graph,
We can say that the marked line is from -6 and continued after -6 till the last number on the right side of the number line.
Hence,
The representation of the given number line in the form of inequality is:
x ≥ -6

Writing and Graphing Inequalities 2.1 Exercises

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
A mathematical sentence using the symbols <, >, ≤, or ≥ is called a(n)_______.
Answer:

Question 2.
VOCABULARY
Is 5 in the solution set of x + 3 > 8? Explain.
Answer:
5 is not in the solution of the given inequality
x + 3 > 8

Explanation:
The given inequality is:
x + 3 > 8
So,
x > 8 – 3
x > 5
Hence, from the above,
We can conclude that 5 is not in the solution of the given inequality

Question 3.
ATTENDING TO PRECISION
Describe how to graph an inequality.
Answer:

Question 4.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” inequalities.

Answer:
The given inequalities in the worded form are:
a) w is greater than or equal to -7
b) w is not less than -7
c) w is no more than -7
d) w is at least -7
Now,
a)
The given worded form in the form of inequality is:
w ≥ -7
b)
The given worded form in the form of inequality is:
w > -7
c)
The given worded form in the form of inequality is:
w ≥ -7
d)
The given worded form in the form of inequality is:
w ≥ -7

Monitoring Progress and Modeling with Mathematics

In Exercises 5–12, write the sentence as an inequality.

Question 5.
A number x is greater than 3.
Answer:

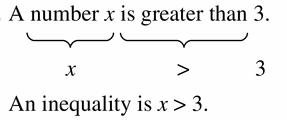
Question 6.
A number n plus 7 is less than or equal to 9.
Answer:
The given worded form is:
A number n plus 7 is less than or equal to 9
Hence,
The representation of the given worded form in the form of inequality is:
n + 7 ≤ 9

Question 7.
Fifteen is no more than a number t divided by 5.
Answer:

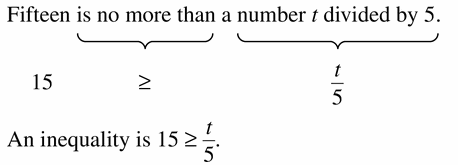
Question 8.
Three times a number w is less than 18.
Answer:
The given worded form is:
Three times a number w is less than 18
Hence,
The representation of the given worded form in the form of inequality is:
3w < 18

Question 9.
One-half of a number y is more than 22.
Answer:

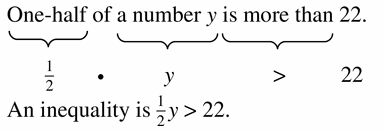
Question 10.
Three is less than the sum of a number s and 4.
Answer:
The given worded form is:
Three is less than the sum of a number s and 4
Hence,
The representation of the given worded form in the form of inequality is:
3 < s + 4

Question 11.
Thirteen is at least the difference between a number v and 1.
Answer:

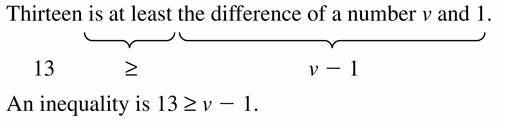
Question 12.
Four is no less than the quotient of a number x and 2.
Answer:
The given worded form is:
Four is no less than the quotient of a number x and 2
Hence,
The representation of the given worded form in the form of inequality is:
4 > x ÷ 2

Question 13.
MODELING WITH MATHEMATICS
On a fishing trip, you catch two fish. The weight of the first fish is shown. The second fish weighs at least 0.5 pound more than the first fish. Write an inequality that represents the possible weights of the second fish.

Answer:

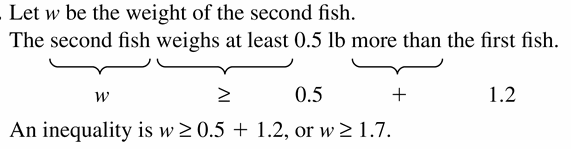
Question 14.
MODELING WITH MATHEMATICS
There are 430 people in a wave pool. Write an inequality that represents how many more people can enter the pool.

Answer:
The inequality that represents the number of more people that can enter the pool is:
430 + x = 600
Where,
x is the number of more people that can enter the pool

Explanation:
It is given that there are 430 people in a wave pool
It is also given that the maximum capacity in a pool is: 600
Let,
x be the number of more people that can enter the pool
Hence,
The inequality that represents the number of more people that can enter the pool is:
430 + x = 600

In Exercises 15–24, tell whether the value is a solution to the inequality.

Question 15.
r + 4 > 8; r = 2
Answer:

Question 16.
5 – x < 8; x = -3
Answer:
-3 is not a solution of the given inequality

Explanation:
The given inequality is:
5 – x < 8
It is given that x = -3
So,
5 – ( -3 ) < 8
5 + 3 < 8
8 < 8
Hence, from the above,
We can conclude that x = -3 is not a solution to the given inequality

Question 17.
3s ≤ 19; s = -6
Answer:

Question 18.
17 ≥ 2y ; y = 7
Answer:
y = 7 is a solution of the given inequality

Explanation:
The given inequality is:
17 ≥ 2y
It is given that y = 7
So,
17 ≥ 2 ( 7 )
17 ≥ 14
Hence, from the above,
We can conclude that y = 7 is a solution of the given inequality

Question 19.
-1 > –\(\frac{x}{2}\); x = 3
Answer:

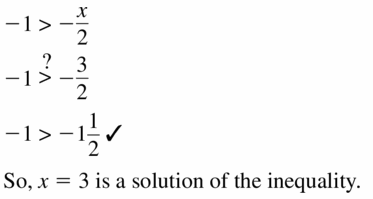
Question 20.
–\(\frac{4}{z}\) ≥ 3; z = 2
Answer:
z = 2 is not a solution of the given inequality

Explanation;
The given inequality is:
–\(\frac{4}{z}\) ≥ 3
It is given that z = 2
So,
–\(\frac{4}{2}\) ≥ 3
-2 ≥ 3
Hence, from the above,
We can conclude that z = 2 is not a solution of the given inequality

Question 21.
14 ≥ -2n + 4; n = -5
Answer:

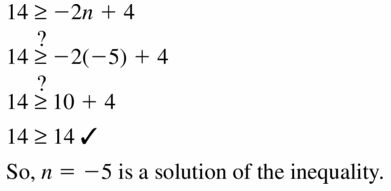
Question 22.
-5 ÷ (2s) < -1; s = 10
Answer:
s = 10 is a solution of the given inequality

Explaantion:
The given inequality is:
-5 ÷ ( 2s ) < -1
It is given that s = 10
So,
-5 ÷ 2 ( 10 ) < -1
-5 ÷ 20 < -1
–\(\frac{1}{4}\) < -1
\(\frac{1}{4}\) < 1
1 < 4
Hence, from the above,
We can conclude that s = 10 is a solution of the given inequality

Question 23.
20 ≤ \(\frac{10}{2z}\) + 20; z = 5
Answer:

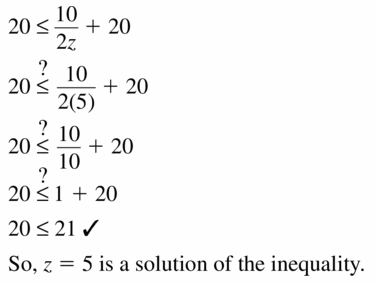
Question 24.
\(\frac{3m}{6}\) – 2 > 3; m = 8
Answer:
m = 8 is not a solution of the given inequality

Explanation:
The given inequality is:
\(\frac{3m}{6}\) – 2 > 3
It is given that m = 8
So,
\(\frac{3 × 8}{6}\) > 3 + 2
4  3 + 2
4 > 5
Hence, from the above,
We can conclude that m = 8 is not a solution of the given inequality

Question 25.
MODELING WITH MATHEMATICS
The tallest person who ever lived was approximately 8 feet 11 inches tall.
a. Write an inequality that represents the heights of every other person who has ever lived.
b. Is 9 feet a solution of the inequality? Explain.

Question 26.
DRAWING CONCLUSIONS
The winner of a weight-lifting competition bench-pressed 400 pounds. The other competitors all bench-pressed at least 23 pounds less.
a. Write an inequality that represents the weights that the other competitors bench-pressed.
Answer:
It is given that the winner of a weight-lifting competition bench pressed 400 pounds whereas the other competitors all bench-pressed at least 23 pounds less.
Let,
x be the number of pounds that all the other competitors’ bench-pressed
So,
The inequality that represents the weights that the other competitors bench-pressed is:
x  + 23 ≤ 400

b. Was one of the other competitors able to bench-press 379 pounds? Explain.
Answer:
No, one of the other competitors won’t be able to bench-press 379 pounds

Explanation:
From part (a),
The inequality that represents the weights that the other competitors bench-pressed is:
x + 23 ≤ 400
x ≤ 400 – 23
x ≤ 377 pounds
Hence, from the above,
We can conclude that one of the other competitors won’t be able to bench-press 379 pounds

ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in determining whether 8 is in the solution set of the inequality.

Question 27.

Answer:

Question 28.

Answer:
8 is a solution set of the given inequality

Explanation:
The given inequality is:
\(\frac{1}{2}\)x + 2 ≤ 6
It is given that x = 8
So,
\(\frac{1}{2}\) × 8 ≤ 6 – 2
\(\frac{8}{2}\) ≤ 4
4 ≤ 4
Hence, from the above,
We can conclude that 8 is a solution set of the given inequality

In Exercises 29–36, graph the inequality.

Question 29.
x ≥ 2
Answer:

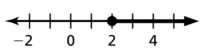
Question 30.
z ≤ 5
Answer:
The given inequality is:
z ≤ 5
Hence,
The representation of the given inequality in the number line is:

Question 31.
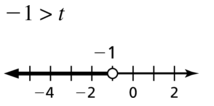
-1 > t
Answer:

Question 32.
-2 < w
Answer:
The given inequality is:
-2 < w
So,
w > -2
Hence,
The representation of the given inequality in the number line is:

Question 33.
v ≤ -4
Answer:

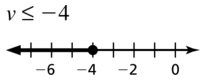
Question 34.
s < 1
Answer:
The given inequality is:
s < 1
Hence,
The representation of the given inequality in the number line is:

Question 35.
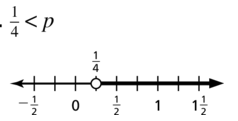
\(\frac{1}{4}\) < p
Answer:

Question 36.
r ≥ -| 5 |
Answer:
The given inequality is:
r ≥ – | 5 |
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
r ≥ -5   ( or ) r ≥ 5
Hence,
The representation of the given inequalities in the number line is:

In Exercises 37–40, write and graph an inequality for the given solution set.

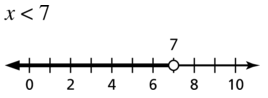
Question 37.
{x | x < 7}
Answer:

Question 38.
{n | n ≥ -2}
Answer:
The given inequality is:
{n | n ≥ -2}
The given inequality can be rewritten as:
n ≥ -2
Hence,
The representation of the given inequality in the number line is:

Question 39.
{z | 1.3 ≤ z}
Answer:

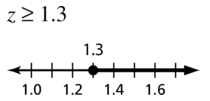
Question 40.
{w | 5.2 > w}
Answer:
The given inequality is:
{w | 5.2 > w}
The given inequality can be rewritten as:
5.2 > w
So,
w < 5.2
From the above value,
We can say that 5.2 lies between 5 and 6
Hence,
The representation of the given inequality in the number line is:

In Exercises 41–44, write an inequality that represents the graph.

Question 41.

Answer:

Question 42.

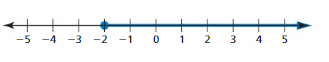
Answer:
The given number line is:

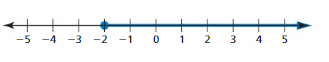
From the above number line,
We can say that the marked line started from -2 and ended at the last value on the right side of the number line.
Hence,
The representation of the inequality for the given number line is:
x ≥ -2

Question 43.

Answer:

Question 44.

Answer:
The given number line is:

From the above number line,
We can say that the marked line started from -1 excluding – and continued till the end of the number line in the left side of the number line
Hence,
The representation of the inequality for the given number line is:
x < -1

Question 45.
ANALYZING RELATIONSHIPS
The water temperature of a swimming pool must be no less than 76°F. The temperature is currently 74°F. Which graph correctly shows how much the temperature needs to increase? Explain your reasoning.

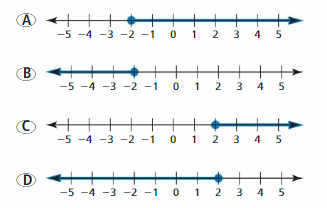
Answer:

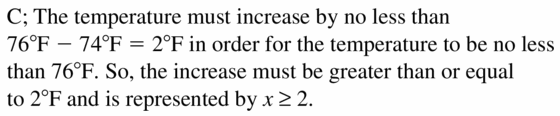
Question 46.
MODELING WITH MATHEMATICS
According to state law for vehicles traveling on state roads, the maximum total weight of a vehicle and its contents depends on the number of axles on the vehicle. For each type of vehicle, write and graph an inequality that represents the possible total weights w (in pounds) of the vehicle and its contents.

Answer:
It is given that the maximum total weight of a vehicle and its contents depends on the number of axles on the vehicle.
Now,
Let,
w be the total weight of the vehicle and its contents
For the 2 axles vehicle, if the maximum weight is 40,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 40,000
The representation of the given inequality in the number line is:

For the 3 axles vehicle, if the maximum weight is 60,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 60,000
The representation of the given inequality in the number line is:

For the 4 axles vehicle, if the maximum weight is 80,000 lb and w is the possible total weight of the vehicle and its contents, then
w < 80,000
The representation of the given inequality in the number line is:

Question 47.
PROBLEM-SOLVING
The Xianren Bridge is located in Guangxi Province, China. This arch is the world’s longest natural arch, with a length of 400 feet. Write and graph an inequality that represents the lengths ℓ (in inches) of all other natural arches.

Answer:

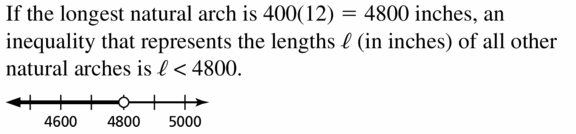
Question 48.
THOUGHT-PROVOKING
A student works no more than 25 hours each week at a part-time job. Write an inequality that represents how many hours the student can work each day.
Answer:
It is given that a student works no more than 25 hours each week at a part-time job
Let the number of days that students work each week be x
So,
The inequality that represents the number of hours the students work each week is:
x < 25
We know that,
1 week = 7 days
So,
7x < 25
Hence,
The inequality that represents the number of hours the students work each day is:
x < \(\frac{25}{7}\)
x < 3.5
Hence,
The representation of the inequality in the number line is:

Question 49.
WRITING
Describe a real-life situation modeled by the inequality 23 + x ≤ 31.
Answer:

Question 50.
HOW DO YOU SEE IT?
The graph represents the known melting points of all metallic elements (in degrees Celsius).
a. Write an inequality represented by the graph.
Answer:
The given graph is:

From the above graph,
We can say that the marked line started from -38.87 and continued till the end of the right line of the number line
Hence,
The inequality that represents the given number line is:
x ≥ -38.87

b. Is it possible for a metallic element to have a melting point of -38.87°C? Explain.
Answer:
Yes, it is possible for a metallic element to have a melting point of -38.87°C.

Explanation:
The given graph is:

From the above graph,
The starting point is -38.87
Hence, from the above,
We can conclude that it is possible for a metallic element to have a melting point of -38.87°C

Question 51.
DRAWING CONCLUSIONS
A one-way ride on a subway costs $0.90. A monthly pass costs $24. Write an inequality that represents how many one-way rides you can buy before it is cheaper to buy the monthly pass. Is it cheaper to pay the one-way fare for 25 rides? Explain.

Answer:

Question 52.
MAKING AN ARGUMENT
The inequality x ≤ 1324 represents the weights (in pounds) of all mako sharks ever caught using a rod and reel. Your friend says this means no one using a rod and reel has ever caught a mako shark that weighs 1324 pounds. Your cousin says this means someone using a rod and reel has caught a mako shark that weighs 1324 pounds. Who is correct? Explain your reasoning.
Answer:
Your cousin is correct

Explanation:
It is given that the inequality x ≤ 1324 represents the weights (in pounds) of all mako sharks ever caught using a rod and reel. Your friend says this means no one using a rod and reel has ever caught a mako shark that weighs 1324 pounds. Your cousin says this means someone using a rod and reel has caught a mako shark that weighs 1324 pounds.
Now,
The given inequality is:
x ≤ 1324
The meaning of inequality is the value of x is less than or equal to 1324 pounds
Now,
Your friend says this means no one using a rod and reel has ever caught a mako shark that weighs 1324 pounds
But, from the given inequality,
The statement of your friend is wrong
Your cousin says this means someone using a rod and reel has caught a mako shark that weighs 1324 pounds
But from the given inequality,
The statement of your cousin is correct.
Hence, from the above,
We can conclude that your cousin is correct

Question 53.
CRITICAL THINKING
Describe a real-life situation that can be modeled by more than one inequality.
Answer:

Question 54.
MODELING WITH MATHEMATICS
In 1997, Superman’s cape from the 1978 movie Superman was sold at an auction. The winning bid was $17,000. Write and graph an inequality that represents the amounts all the losing bids.
Answer:
It is given that in 1997, Superman’s cape from the 1978 movie Superman was sold at an auction. The winning bid was $17,000.
So,
The bid must not be less than $17,000, otherwise, the bid will lose
Hence,
The inequality that represents the amounts of all losing bids is:
x < 17,000
The representation of the inequality in the number line is:

MATHEMATICAL CONNECTIONS
In Exercises 55–58, write an inequality that represents the missing dimension x.

Question 55.
The area is less than 42 square meters.

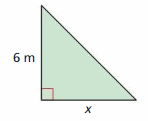
Answer:

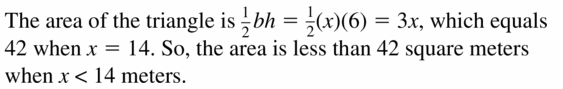
Question 56.
The area is greater than or equal to 8 square feet.

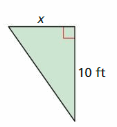
Answer:
The inequality that represents the value of x is:
x ≥ \(\frac{8}{5}\)

Explanation:
The given figure is:

From the above figure,
We can say that the given figure is a Right-angled triangle
We know that,
The area of the triangle = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × x × 10
= 5x
It is given that the area of the triangle is greater than or equal to 8 square feet
So,
5x ≥ 8 square feet
x ≥ \(\frac{8}{5}\)
Hence, from the above,
We can conclude that the inequality that represents x is:
x ≥ \(\frac{8}{5}\)

Question 57.
The area is less than 18 square centimeters.

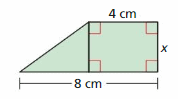
Answer:

Question 58.
The area is greater than 12 square inches.

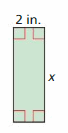
Answer:
The inequality that represents the value of x is:
x > 6

Explanation:
The given figure is:

From the above figure,
We can say that the given figure is the rectangle.
We know that,
The area of the rectangle = Length × Width
= 2 × x
It is given that the area of the rectangle is greater than 12 square inches
So,
2x > 12
x > 12 / 2
x > 6
Hence, from the above,
We can conclude that the inequality that represents the value of x is:
x > 6

Question 59.
WRITING
A runner finishes a 200-meter dash in 35 seconds. Let r represent any speed (in meters per second) faster than the runner’s speed.
a. Write an inequality that represents r. Then graph the inequality.
b. Every point on the graph represents a speed faster than the runner’s speed. Do you think every point could represent the speed of a runner? Explain.
Answer:

Maintaining Mathematical Proficiency

Solve the equation. Check your solution.(Section 1.1)

Question 60.
x + 2 = 3
Answer:
The value of x is: 1

Explanation:
The given equation is:
x + 2 = 3
So,
x = 3 – 2
x = 1
Hence, from the above
We can conclude that the value of x is: 1

Question 61.
y – 9 = 5
Answer:

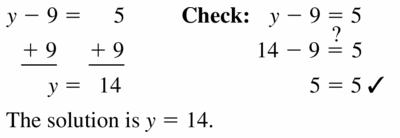
Question 62.
6 = 4 + y
Answer:
The value of y is: 2

Explanation:
The given equation is:
6 = 4 + y
So,
6 – 4 = y
2 = y
y = 2
Hence, from the above,
We can conclude that the value of y is: 2

Question 63.
-12 = y – 11
Answer:

Solve the literal equation for x.(Section 1.5)

Question 64.
v = x • y • z
Answer:
The value of x is: \(\frac{v}{yz}\)

Explanation:
The given equation is:
v = x ⋅ y ⋅ z
x = \(\frac{v}{yz}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{v}{yz}\)

Question 65.
s = 2r + 3x
Answer:

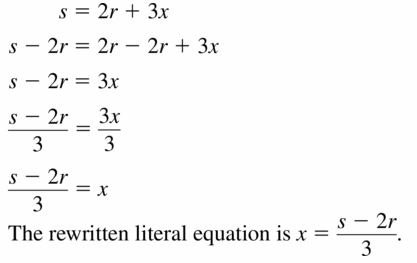
Question 66.
w = 5 + 3(x – 1)
Answer:
The value of x is: \(\frac{w – 2}{3}\)

Explanation:
The given equation is:
w = 5 + 3 ( x – 1 )
So,
w = 5 + 3 ( x ) – 3 ( 1 )
w = 5 + 3x – 3
w = 3x + 2
3x = w – 2
x = \(\frac{w – 2}{3}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{w – 2}{3}\)

Question 67.
n = \(\frac{2x + 1}{2}\)
Answer:

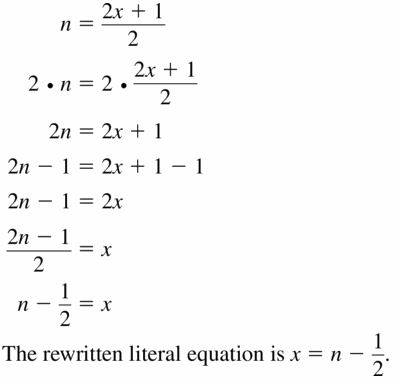
Lesson 2.2 Solving Inequalities Using Addition or Subtraction

Essential Question
How can you use addition or subtraction to solve an inequality?
EXPLORATION 1
Quarterback Passing Efficiency
Work with a partner.
The National Collegiate Athletic Association (NCAA) uses the following formula to rank the passing efficiencies P of quarterbacks.

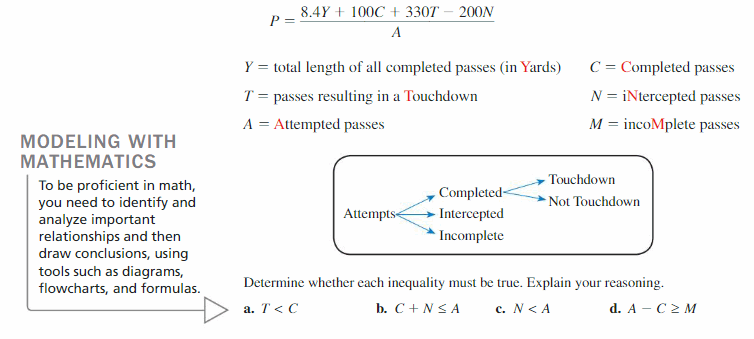
Answer:
The formula used to rank the passing efficiencies P of the quarterbacks is:

By comparing the coefficients, we get
Y = 8.4
C = 100
T = 330
N = 200
A = 1
Now,
a) T < C
= 330 < 100
Hence, from the above,
We can conclude that the given inequality is not true
b) C + N ≤ A
= ( 100 + 200 ) ≤ 1
= 300 ≤ 1
Hence, from the above,
We can conclude that the given inequality is not true
c) N < A
= 200 < 1
Hence, from the above,
We can conclude that the given inequality is not true
d) A – C ≥ M
We know that,
M = C – N
So,
A-C ≥ C – N
( 1 – 100 ) ≥ ( 100 – 200 )
= -99 ≥ -100
= 99 ≥ 100
Hence, from the above,
We can conclude that the given inequality is not true

EXPLORATION 2
Finding Solutions of Inequalities
Work with a partner.
Use the passing efficiency formula to create a passing record that makes each inequality true. Record your results in the table. Then describe the values of P that make each inequality true.

a. P < 0
b. P + 100 ≥ 250
c. P – 250 > -80
Answer:
Using the data from Exploration 1,
The completed table is:

Now,
The formula for passing efficiency is:

a) P < 0
To make P < 0,
The value of A or any of the values of the numerator must be less than 0
b) P + 100 ≥ 250
P ≥ 250 – 100
P ≥ 150
Hence, from the above,
We can conclude that the value of P must be greater than or equal to 150
c ) P – 250 > -80
P > -80 + 250
P > 170
Hence, from the above,
We can conclude that the value of P must be greater than 170

Communicate Your Answer

Question 3.
How can you use addition or subtraction to solve an inequality?
Answer:
If you want to add or subtract from one side of the equation, you must perform the same operation to the other side of the equation. When solving inequalities by adding or subtracting, our goal is to have the variable on its own

Question 4.
Solve each inequality.
a. x + 3 < 4 b. x – 3 ≥ 5 c. 4 > x – 2
d. -2 ≤ x + 1
Answer:
The given inequalities are:
a) x + 3 < 4
b) x – 3 ≥ 5
c) 4 > x – 2
d) -2 ≤ x + 1
Now,
a)
The given inequality is:
x + 3 < 4
So,
x < 4 – 3
x < 1
Hence, from the above,
We can conclude that x < 1
b)
The given inequality is:
x – 3 ≥ 5
x ≥ 5 + 3
x ≥ 8
Hence, from the above,
We can conclude that x ≥ 8
c)
The given inequality is:
4 > x – 2
So,
4 + 2 > x
6 > x
x < 6
Hence, from the above,
We can conclude that x < 6
d)
The given inequality is:
-2 ≤ x + 1
So,
-2 – 1 ≤ x
-3 ≤ x
x ≥ -3
Hence, from the above,
We can conclude that x ≥ -3

2.2 Lesson

Monitoring Progress

Solve the inequality. Graph the solution.

Question 1.
b – 2 > -9
Answer:
The given inequality is:
b – 2 > -9
So,
b > -9 + 2
b > -7
Hence, from the above,
We can conclude that the value of b is greater than -7
The representation of the inequality in the number line is:

Question 2.
m – 3 ≤ 5
Answer:
The given inequality is:
m – 3 ≤ 5
So,
m ≤ 5 + 3
m ≤ 8
Hence, from the above,
We can conclude that the value of m is less than or equal to 8
The representation of the inequality in the number line is:

Question 3.
\(\frac{1}{4}\) > y – \(\frac{1}{4}\)
Answer:
The given inequality is:
\(\frac{1}{4}\) > y – \(\frac{1}{4}\)
So,
\(\frac{1}{4}\) + \(\frac{1}{4}\) > y
\(\frac{1 + 1}{4}\) > y
\(\frac{2}{4}\) > y
\(\frac{1}{2}\) > y
y < \(\frac{1}{2}\)
Hence, from the above,
We can conclude that the value of y is less than \(\frac{1}{2}\)
The representation of the inequality in the number line is:

Solve the inequality. Graph the solution.

Question 4.
k + 5 ≤ -3
Answer:
The given inequality is:
k + 5 ≤ -3
So,
k ≤ -3 – 5
k ≤ -8
Hence, from the above,
We can conclude that the value of k is less than or equal to -8
The representation of the inequality in the number line is:

Question 5.
\(\frac{5}{6}\) ≤ z + \(\frac{1}{6}\)
Answer:
The given inequality is:
\(\frac{5}{6}\) ≤ z + \(\frac{1}{6}\)
So,
\(\frac{5}{6}\) – \(\frac{1}{6}\) ≤ z
\(\frac{5 – 1}{6}\) ≤ z
\(\frac{4}{6}\) ≤ z
\(\frac{2}{3}\) ≤ z
z ≥ \(\frac{2}{3}\)
z ≥ 0.6
z ≥ 1 ( Approx. )
Hence, from the above,
We can conclude that the value of z is approximately greater than or equal to 1
The representation of the inequality in the number line is:

Question 6.
p + 0.7 > -2.3
Answer:
The given inequality is:
p + 0.7 > -2.3
So,
p > -2.3 – 0.7
p > -3
Hence, from the above,
We can conclude that the value of p is greater than -3
The representation of the inequality in the number line is:

Monitoring Progress

Question 7.
The microwave oven uses only 1000 watts of electricity. Does this allow you to have both the microwave oven and the toaster plugged into the circuit at the same time? Explain your reasoning.
Answer:
Yes, this allows you to have both the microwave oven and the toaster plugged into the circuit at the same time

Explanation:
It is given that the microwave oven uses only 1000 watts of electricity.
We know that,
The toaster consumes less electricity than the microwave oven
Hence, from the above,
We can conclude that 1000 watts of electricity allow you to have both the microwave oven and the toaster plugged into the circuit at the same time

Solving Inequalities Using Addition or Subtraction 2.2 Exercises

In Exercises 3−6, tell which number you would add to or subtract from each side of the inequality to solve it.

Question 1.
VOCABULARY
why is the inequality x ≤ 6 equivalent to the inequality x – 5 ≤ 6 – 5 ?
Answer:

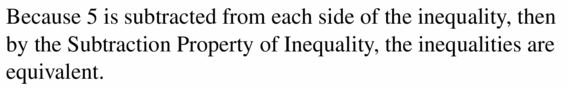
Question 2.
WRITING
Compare solving equations using addition with solving inequalities using addition.
Answer:
Solving equations and inequalities using addition is very similar. You have to add the same quantity on every side and the sign between the two sides does not change.
It remains the equal sign  “=”  in the case of equations and the inequality sign in the case of inequalities

Question 3.
k + 11 < -3
Answer:

Question 4.
v – 2 > 14
Answer:
The value of v is: 16

Explanation:
The given equation is:
v – 2 > 14
So,
v  – 2 + 2 > 14 + 2
v > 16
Hence, from the above,
We can conclude that we have to add 2 on both sides

Question 5.
-1 ≥ b – 9
Answer:

Question 6.
-6 ≤ 17 + p
Answer:
The value of p is: p ≥ -23

Explanation:
The given inequality is:
-6 ≤ 17 + p
So,
-6 + 6 ≤ 17 + 6 + p
0 ≤ 23 + p
-23 ≤ p
p ≥ -23
Hence, from the above,
We can conclude that we have to add 6 on both sides

In Exercises 7−20, solve the inequality. Graph the solution.

Question 7.
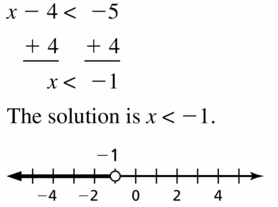
x – 4 < -5
Answer:

Question 8.
1 ≤ s – 8
Answer:
The given inequality is:
1 ≤ s – 8
1 + 8 ≤ s – 8 + 8
9 ≤ s
s ≥ 9
Hence,
The solution to the given inequality is:
s ≥ 9
The representation of the inequality in the number line is:

Question 9.
6 ≥ m – 1
Answer:

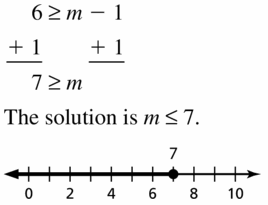
Question 10.
c – 12 > -4
Answer:
The given inequality is:
c – 12 > -4
So,
c – 12 + 4 > -4 + 4
c – 8 > 0
c > 0 + 8
c > 8
Hence, from the above,
We can conclude that the solution to the given inequality is:
c > 8
The representation of the inequality in the number line is:

Question 11.
r + 4 < 5
Answer:

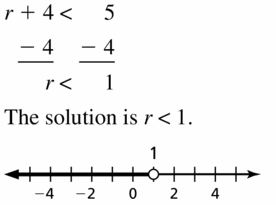
Question 12.
-8 ≤ 8 + y
Answer:
The given inequality is:
-8 ≤ 8 + y
So,
-8 + 8 ≤ 8 + 8 + y
0 ≤ 16 + y
-16 ≤ y
y ≥ -16
Hence, from the above,
We can conclude that the solution to the given inequality is:
y ≥ -16
The representation of the inequality in the number line is:

Question 13.
9 + w > 7
Answer:

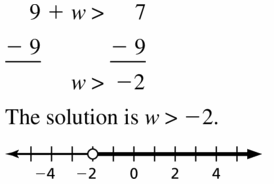
Question 14.
15 ≥ q + 3
Answer:
The given inequality is:
15 ≥ q + 3
So,
15 – 15 ≥ q + 3 – 15
0 ≥ q – 12
12 ≥ q
q ≤ 12
Hence, from the above,
We can conclude that the solution to the given inequality is:
q ≤ 12
The representation of the inequality in the number line is:

Question 15.
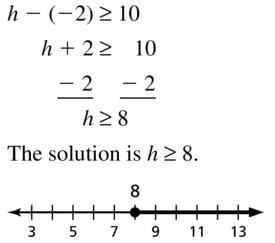
h – (-2) ≥ 10
Answer:

Question 16.
-6 > t – (-13)
Answer:
The given inequality is:
-6 > t – ( -13 )
So,
-6 + 6 > t + 13 + 6
0 > t + 19
-19 > t
t < -19
Hence, from the above,
We can conclude that the solution to the given inequality is:
t < -19
The representation of the inequality in the number line is:

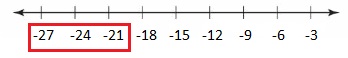
Question 17.
j + 9 – 3 < 8
Answer:

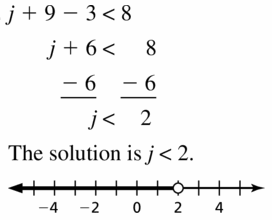
Question 18.
1 – 12 + y ≥ -5
Answer:
The given inequality is:
1 – 12 + y ≥ -5
So,
-11 + y ≥ -5
-11 + 5 + y ≥ -5 + 5
6 + y ≥ 0
y ≥ -6
Hence, from the above,
We can conclude that the solution to the given inequality is:
y ≥ -6
The representation of the inequality in the number line is:

Question 19.
10 ≥ 3p – 2p – 7
Answer:

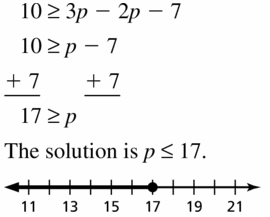
Question 20.
18 – 5z + 6z > 3 + 6
Answer:
The given inequality is:
18 – 5z + 6z > 3 + 6
So,
18 + z > 9
18 – 9 + z > 9 – 9
z + 9 > 0
z > -9
Hence, from the above,
We can conclude that the solution to the given inequality is:
z > -9
The representation of the inequality in the number line is:

In Exercises 21−24, write the sentence as an inequality. Then solve the inequality.

Question 21.
A number plus 8 is greater than 11.
Answer:

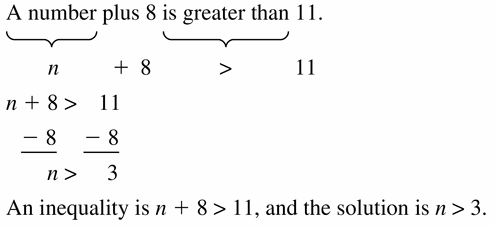
Question 22.
A number minus 3 is at least -5.
Answer:
The given worded form is:
A number minus 3 is at least -5
Let the number be x
So,
The representation of the given worded form in the form of inequality is:
x – 3 ≥ -5
So,
x – 3 + 5 ≥ -5 + 5
x + 2 ≥ 0
x ≥ -2
Hence, the solution to the given worded form inequality is:
x ≥ -2

Question 23.
The difference of a number and 9 is fewer than 4.
Answer:

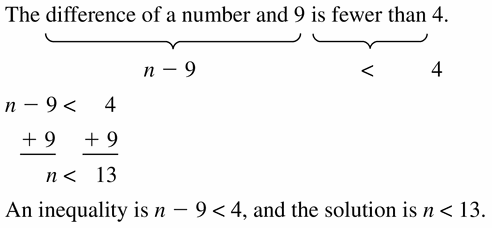
Question 24.
Six is less than or equal to the sum of a number and 15.
Answer:
The given worded form is:
Six is less than or equal to the sum of a number and 15
Let the number be x
So,
The representation of the given worded form in the form of inequality is:
6 ≤ x + 15
6 – 6 ≤ x + 15 – 6
0 ≤ x + 9
-9 ≤ x
x ≥ -9
Hence, from the above,
We can conclude that the solution to the given worded form of the inequality is:
x ≥ -9

Question 25.
MODELING WITH MATHEMATICS
You are riding a train. Your carry-on bag can weigh no more than 50 pounds. Your bag weighs 38 pounds.
a. Write and solve an inequality that represents how much weight you can add to your bag.
b. Can you add both a 9-pound laptop and a 5-pound pair of boots to your bag without going over the weight limit? Explain.
Answer:

Question 26.
MODELING WITH MATHEMATICS
You order the hardcover book shown from a website that offers free shipping on orders of $25 or more. Write and solve an inequality that represents how much more you must spend to get free shipping.

Answer:
The inequality that represents the more money you must spend to get free shipping is:

Explanation:
It is given that you order the hardcover book shown from a website that offers free shipping on orders of $25 or more.
From the figure,
The cost of a hardcover book is: $19.76
Let
The amount more money you must spend to get free shipping to be x
So,
x + 19.76 ≥ 25
x + 19.76 – 25 ≥ 25 – 25
x – 5.24 ≥ 0
x ≥ $5.24
Hence, from the above,
We can conclude that the amount more money you must spend to get free shipping is: $5.24
ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in solving the inequality or graphing the solution.

Question 27.

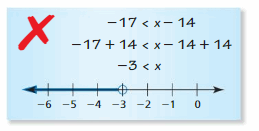
Answer:

Question 28.

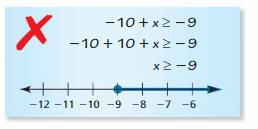
Answer:
The given inequality is:
-10 + x ≥ -9
-10 + 9 + x ≥ -9 + 9
-1 + x ≥ 0
x ≥ 1
Hence, from the above,
We can conclude that the solution to the given inequality is:
x ≥ 1
The representation of the inequality in the number line is:

Question 29.
PROBLEM-SOLVING
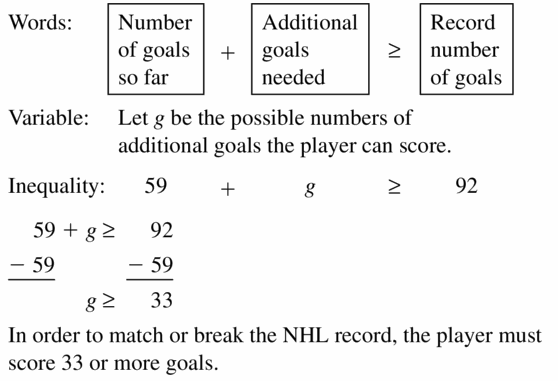
An NHL hockey player has 59 goals so far in a season. What are the possible numbers of additional goals the player can score to match or break the NHL record of 92 goals in a season?
Answer:

Question 30.
MAKING AN ARGUMENT
In an aerial ski competition, you perform two acrobatic ski jumps. The scores on the two jumps are then added together.

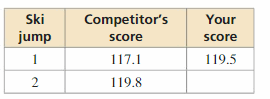
a. Describe the score that you must earn on your second jump to beat your competitor.
Answer:
The given table is:

Let the score of your second acrobatic ski jump be x
Now,
From the above table,
We can say that your score must be greater than your competitor’s score to beat your competitor
Hence,
The inequality that represents the score you must earn on your second jump to beat your competitor is:
x > 119.8

b. Your coach says that you will beat your competitor if you score 118.4 points. A teammate says that you only need 117.5 points. Who is correct? Explain.
Answer:
Your coach and your teammate both are correct

Explanation:
The given table is:

From the above table,
In the 1st acrobatic ski jump,
Your competitor’s score is: 117.1
Your score is: 119.5
If you want to beat your competitor, then you have to score more than 117.1
So,
x > 117.1
It is given that your coach says that you will beat your competitor if you score 118.4 points. A teammate says that you only need 117.5 points
So,
According to your coach,
You have to score 118.4 points to beat your competitor
So,
118.4 > 117.1
According to a teammate,
You have to score 117.5 points to beat your competitor
So,
117.5 > 117.1
Hence, from the above,
We can conclude that your coach and your teammate both are correct

Question 31.
REASONING
Which of the following inequalities are equivalent to the inequality x – b < 3, where b is a constant? Justify your answer.

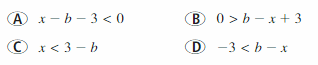
Answer:

MATHEMATICAL CONNECTIONS
In Exercises 32 and 33, write and solve an inequality to find the possible values of x.

Question 32.
Perimeter < 51.3 inches

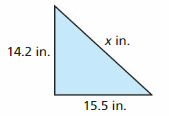
Answer:
The value of x is greater than 21.6 inches

Explanation:
The given figure is:

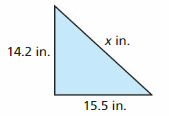
From the above figure,
We can say that the figure is the triangle
We know that,
The perimeter is the sum of all of the sides
So,
The perimeter of the triangle = 15.5 + 14.2 + x
It is given that
Perimeter < 51.3 inches
So,
51.3 < 29.7 + x
51.3 – 29.7 < x
21.6 < x
x > 21.6
Hence, from the above,
We can conclude that the value of x is greater than 21.6 inches

Question 33.
Perimeter ≤ 18.7 feet

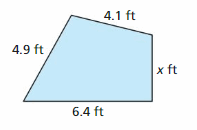
Answer:

Question 34.
THOUGHT-PROVOKING
Write an inequality that has the solution shown in the graph. Describe a real-life situation that can be modeled by inequality.

Answer:
The given number line is:

From the above number line,
We can observe that the marked line is starting from 16 and continued till the left end of the number line
So,
The inequality that represents the given number line is:
x ≤ 16
The real-life situation that can be modeled by inequality is:
A lift carrying no more than 16 people

Question 35.
WRITING
Is it possible to check all the numbers in the solution set of an inequality? When you solve the inequality x – 11 ≥ -3, which numbers can you check to verify your solution? Explain your reasoning.
Answer:

Question 36.
HOW DO YOU SEE IT?
The diagram represents the numbers of students in a school with brown eyes, brown hair, or both.

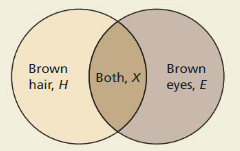
Determine whether each inequality must be true. Explain your reasoning.
a. H ≥ E
b. H + 10 ≥ E
c. H ≥ X
d. H + 10 ≥ X
e. H > X
f. H + 10 > X
Answer:
The given diagram is:

From the above diagram,
We can observe that,
The spaces occupied by H and E are equal
The spaces occupied by H and E are greater than X
So,
We can say that
H = E; H > X; E > X
Now,
a. H ≥ E
From the above diagram,
The given inequality is not true
b. H + 10 ≥ E
From the above diagram,
The given inequality is not true
c. H ≥ X
From the above diagram,
The given inequality is not true
d. H + 10 ≥ X
From the above diagram,
The given inequality is not true
e. H > X
From the above diagram,
The given inequality is true
f. H + 10 > X
From the above diagram,
The given inequality is true

Question 37.
REASONING
Write and graph an inequality that represents the numbers that are not solutions to each inequality.
a. x + 8 < 14
b. x – 12 ≥ 5.7
Answer:

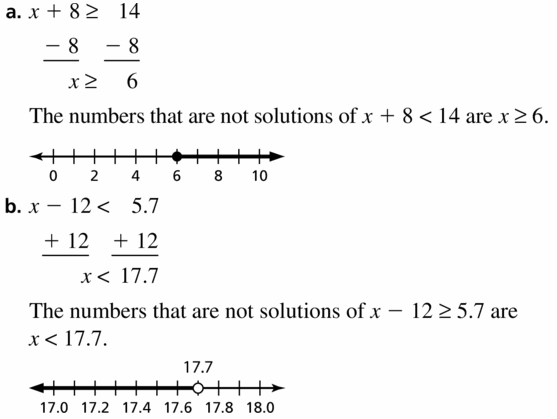
Question 38.
PROBLEM-SOLVING
Use the inequalities c – 3 ≥ d, b + 4 < a + 1, and a – 2 ≤ d – 7 to order a, b, c, and d from least to greatest.
Answer:
The order of a, b, c, and d from least to greatest is:
b, a, c, and d

Explanation:
The given inequalities are:
A) c – 3 ≥ d
B) b + 4 < a + 1
C) a – 2 ≤ d – 7
Now,
A)
The given inequality is:
c – 3 ≥ d
c ≥ d + 3
B)
The given inequality is:
b + 4 < a + 1
b < a + 1 – 4
b < a – 3
b + 3 < a
a > b + 3
C)
The given inequality is:
a – 2 ≤ d – 7
a ≤ d – 7 + 2
a ≤ d – 5
a + 5 ≤ d
d ≥ a + 5
Hence, from the above,
We can conclude that the order of a, b, c, d from least to greatest is:
b, a, c, and d

Maintaining Mathematical Proficiency

Find the product or quotient.

Question 39.
7 • (-9)
Answer:

Question 40.
-11 • (-12)
Answer:
The given expression is:
-11 ⋅ ( -12 )
= 11 ⋅ 12 [ Since we know that – × – = + ]
= 132
Hence, from the above,
We can conclude that the product of the given expression is: 132

Question 41.
-27 ÷ (-3)
Answer:

Question 42.
20 ÷ (-5)
Answer:
The given expression is:
20 ÷ ( -5 )
= -20 ÷ 5 [ Since we know that + ÷ – = – ]
= -4
Hence, from the above,
We can conclude that the product of the given expression is: -4

Solve the equation. Check your solution.(Section 1.1)

Question 43.
6x = 24
Answer:

Question 44.
-3y = -18
Answer:
The given equation is:
-3y = -18
y = -18 ÷ ( -3 )
y = 6 [ Sice we know that – ÷ – = + ]
Hence, fro the above,
We can conclude that the value of y in the given equation is: 6

Question 45.
\(\frac{s}{-8}\) = 13
Answer:

Question 46.
\(\frac{n}{4}\) = -7.3
Answer:
The given equation is:
\(\frac{n}{4}\) = -7.3
n = -7.3 × 4
n = -29.2
Hence, from the above,
We can conclude that the value of n in the given equation is: -29.2

Lesson 2.3 Solving Inequalities Using Multiplication or Division

Essential Question

How can you use division to solve inequality?

EXPLORATION 1
Writing a Rule
Work with a partner.
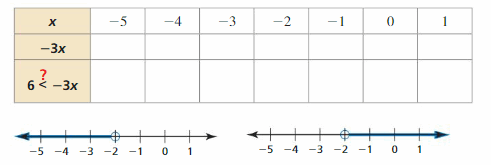
a. Copy and complete the table. Decide which graph represents the solution of the inequality 6 < 3x. Write the solution to the inequality.

Answer:
a)
The completed table is:

The given number lines are:

From the above two number lines,
We can say that the expression 6 < 3x will be true if the value of x is greater than 2
From the 2nd number line,
We can observe that the value of x is greater than 2
b)
Rule:
Division Property of Inequality:
If you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.The given inequality is:
6 < 3x
3x > 6
x > 6 ÷ 3
x > 2
So,
From the table,
x > 2 means x = 3, 4, 5
So,
The value of x is: 3, 4, 5
Now,
i. 2x < 4
Answer:
The given inequality is:
2x < 4
x < 4 / 2
x < 2
Now,
From the above table,
We can observe that x < 2 will be held true if the value of x is -1, 0, 1

ii. 3 ≥ 3x
Answer:
The given inequality is:
3 ≥ 3x
1 ≥ x
x ≤ 1
Now,
From the above table,
We can observe that x ≤ 1 will be held true if the value of the x is -1, 0, 1

iii. 2x < 8
Answer:
The given inequality is:
2x < 8
x < 8 / 2
x < 4
Now,
From the above table,
We can observe that x < 4 will be held true if the value of x is -1, 0, 1, 2, 3

iv. 6 ≥ 3x
Answer:
The given inequality is:
6 ≥ 3x
So,
6 / 3 ≥ x
2 ≥ x
x ≤ 2
Now,
from the above table,
We can observe that x ≤ 2 will be held true if the value of x is -1, 0, 1, 2

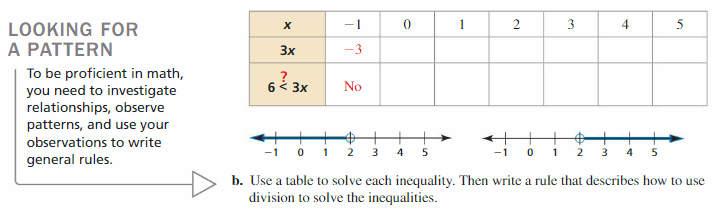
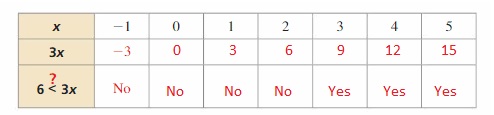
EXPLORATION 2
Writing a Rule
Work with a partner.
a. Copy and complete the table. Decide which graph represents the solution of the inequality 6 < -3x. Write the solution of the inequality.

Answer:
The complete table is:

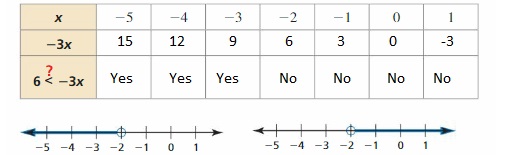
From the given number lines,
The first graph indicates the inequality
x < -2
The second graph indicates the inequality
x > -2
Hence, from the table and the number line,
The inequality that represents the table is:
x < -2

b. Use a table to solve each inequality. Then write a rule that describes how to use division to solve the inequalities.
Rule:
Division Property of Inequality:
If you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.
i. -2x < 4
Answer:
The given inequality is:
-2x < 4
-x < 4 / 2
-x < 2
x < -2
Hence,
From the above table,
We can observe that the values of x for the inequality x < -2 is -5, -4, -3

ii. 3 ≥ -3x
Answer:
The given inequality is:
3 ≥ -3x
1 ≥ -x
-1 ≥ x
x ≤ -1
Hence,
From the above table,
We can observe that the values of x for the inequality x ≤ -1 is -5, -4, -3, -2, -1

iii. -2x < 8
Answer:
The given inequality is:
-2x < 8
x < -8 /2
x < -4
Hence,
From the above table,
We can observe that the values of x for the inequality x < -4 is  -5

iv.6 ≥ -3x
Answer:
The given inequality is:
6 ≥ -3x
6 / ( -3 ) ≥ x
-2 ≥ x
x ≤ -2
Hence,
From the above table,
We can observe that the values of x for the inequality x ≤ -2 is -5, -4, -3, -2

Communicate Your Answer

Question 3.
How can you use division to solve inequality?
Answer:
You can use division to solve the inequality by using the Division Property of Inequality
Division Property of Inequality:
If you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.

Question 4.
Use the rules you wrote in Explorations 1(b) and 2(b) to solve each inequality.
a. 7x < -21
b. 12 ≤ 4x
c. 10 < -5x d. -3x ≤ 0
Answer:
Rule:
Division Property of Inequality:
If you divide one side of an inequality by a number, you can divide the other side of the inequality by the same number.
By using the above rule, solve the given inequalities
Now,
a. 7x < -21
Answer:
The given inequality is:
7x < -21
x < -21 /
x < -3
Hence, from the above,
We can conclude that the solution to the given inequality is x < -3

b. 12 ≤ 4x
Answer:
The given inequality is:
12 ≤ 4x
12 / 4 ≤ x
3 ≤ x
x ≥ 3
Hence, from the above,
We can conclude that the solution to the given inequality is x ≥ 3

c. 10 < -5x
Answer:
The given inequality is:
10 < -5x
10 / -5 < x
2 < x
x > 2
Hence, from the above,
We can conclude that the solution to the given inequality is x > 2

d. -3x ≤ 0
Answer:
The given inequality is:
-3x ≤ 0
x ≤ 0 / -3
x ≤ 0
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 0

2.3 Lesson 

Monitoring Progress Solve the inequality. Graph the solution. 

Question 1.
\(\frac{n}{7}\) ≥ -1
Answer:
The given inequality is:
\(\frac{n}{7}\) ≥ -1
n ≥ -1 ( 7 )
n ≥ -7
Hence, from the above,
We can conclude that the solution o the inequality is n ≥ -7
The representation of the inequality in the number line is:

Question 2.
-6.4 ≥ \(\frac{1}{5}\)w
Answer:
The given inequality is:
-6.4 ≥ \(\frac{1}{5}\)w
-6.4 ( 5 ) ≥ w
-32 ≥ w
w ≤ -32
Hence, from the above,
We can conclude that the solution to the given inequality is w ≤ -32
The representation of the inequality in the number line is:

Question 3.
4b ≥ 36
Answer:
The given inequality is:
4b ≥ 36
b ≥ 36 / 4
b ≥ 9
Hence, from the above,
We can conclude that the solution to the given inequality is b ≥ 9
The representation of the inequality in the number line is:

Question 4.
-18 > 1.5q
Answer:
The given inequality is:
-18 > 1.5q
-18 / 1.5 > q
-180 / 15 > q
-12 > q
q < -12
Hence, from the above,
We can conclude that the solution to the given inequality is q < -12
The representation of the inequality in the number line is:

Monitoring Progress

Solve the inequality. Graph the solution.

Question 5.
\(\frac{p}{-4}\) < 7
Answer:
The given inequality is:
\(\frac{p}{-4}\) < 7
–\(\frac{p}{4}\) < 7
-p < 7 ( 4 )
-p < 28
p < -28
Hence, from the above,
We can conclude that the solution to the given inequality is p < -28
The representation of the inequality in the number line is:

Question 6.
\(\frac{x}{-5}\) ≤ -5
Answer:
The given inequality is:
\(\frac{x}{-5}\) ≤ -5
–\(\frac{x}{5}\) ≤ -5
\(\frac{x}{5}\) ≤ 5
x ≤ 5 ( 5 )
x ≤ 25
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 25
The representation of the inequality in the number line is:

Question 7.
-1 ≥ –\(\frac{1}{10}\)z
Answer:
The given inequality is:
-1 ≥ –\(\frac{1}{10}\)z
1 ≥ \(\frac{1}{10}\)z
1 ( 10 ) ≥ z
10 ≥ z
z ≤ 10
Hence, from the above,
We can conclude that the solution to the given inequality is z ≤ 10
The representation of the inequality in the number line is:

Question 8.
-9m > 63
Answer:
The given inequality is:
-9m > 63
m > -63 / 9
m > -7
Hence, from the above
We can conclude that the solution to the given inequality is m > -7
The representation of the inequality in the number line is:

Question 9.
-2r ≥ -22
Answer:
The given inequality is:
-2r ≥ -22
2r ≥ 22
r ≥ 22 / 2
r ≥ 11
Hence, from the above
We can conclude that the solution to the given inequality is r ≥ 11
The representation of the inequality in the number line is:

Question 10.
-0.4y ≥ -12
Answer:
The given inequality is:
-0.4y ≥ -12
0.4y ≥ 12
y ≥ 12 / 0.4
y ≥ 120 / 4
y ≥ 30
Hence, from the above
We can conclude that the solution to the given inequality is y ≥ 30
The representation of the inequality in the number line is:

Question 11.
You have at most $3.65 to make copies. Each copy costs $0.25. Write and solve an inequality that represents the number of copies you can make.
Answer:
The inequality that represents the number of copies you can make is:
x + 0.25 ≤ 3.65

Explanation:
It is given that you have at most $3.65 i.e., you have a maximum of only $3.65 to make copies and it is also given that each copy costs $0.25.
Let,
The additional cost to make the copies be $x
So,
The total cost = x + 0.25
But,
The total cost won’t be greater than 3.65
Hence,
The inequality that represents the number of copies you can make is:
x + 0.25 ≤ 3.65

Question 12.
The maximum speed limit for a school bus is 55 miles per hour. Write and solve an inequality that represents the number of hours it takes to travel 165 miles in a school bus.
Answer:
The inequality that represents the number of hours it takes to travel 165 miles in a school bus is:
x ≥ 3

Explanation:
It is given that the maximum speed limit for a school bus is 55 miles per hour.
Let,
x be the number of hours
So,
The inequality that represents the number of hours it takes to travel 165 miles in a school bus is:
55x ≥ 165
x ≥ 165 / 55
x ≥ 3
Hence, from the above,
We can conclude that the inequality that represents the number of hours it takes to travel 165 miles in a school bus is:
x ≥ 3

Solving Inequalities Using Multiplication or Division 2.3 Exercises

In Exercises 3–10, solve the inequality. Graph the solution.

Vocabulary and Core Concept Check

Question 1.
WRITING
Explain how solving 2x < -8 is different from solving -2x < 8
Answer:

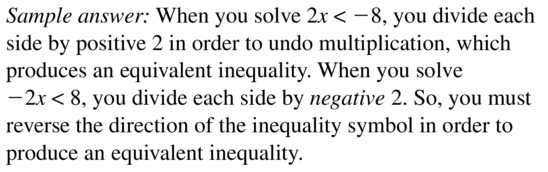
Question 2.
OPEN-ENDED
Write an inequality that is solved using the Division property of Inequality where the inequality symbol needs to be reversed.
Answer:
The required inequality is:
-6 < 3x
Using the Division Property of Inequality,
-6 / 3 < ( 3 / 3 )x
-2 < x
x > -2
Hence, from the above,
We can conclude that the inequality is solved using the Division Property of Inequality wheer the inequality symbol needs to be reversed

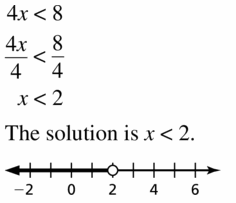
Question 3.
4x < 8
Answer:

Question 4.
3y ≤ -95.
Answer:
The given inequality is:
3y ≤ -95
y ≤ -95 / 3
y ≤ -31.6
y ≤ -32 [ Approximate value ]
Hence, from the above,
We can conclude that the solution to the given inequality is y ≤ -32
The representation of the inequality in the number line is:

Question 5.
-20 ≤ 10n
Answer:

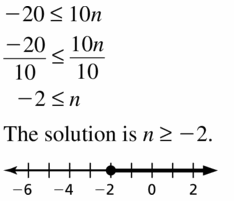
Question 6.
35 < 7t
Answer:
The given inequality is:
35 < 7t
35 / 7 < t
5 < t
t > 5
Hence, from the above,
We can conclude that the solution to the given inequality is t > 5
The representation of the inequality in the number line is:

Question 7.
\(\frac{x}{2}\) > -2
Answer:

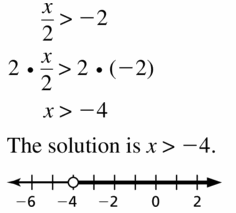
Question 8.
\(\frac{a}{4}\) < 10.2
Answer:
The given inequality is:
\(\frac{a}{4}\) < 10.2
a < 10.2 ( 4 )
a < 40.8
a < 40 [ Approximate value ]
Hence, from the above,
We can conclude that the solution to the given inequality is a < 40
The representation of the inequality in the number line is:

Question 9.
20 ≥ \(\frac{4}{5}\)w
Answer:

Question 10.
-16 ≤ \(\frac{8}{3}\)t
Answer:
The given inequality is:
-16 ≤ \(\frac{8}{3}\)t
-16 ( 3) ≤ 8t
-48 ≤ 8t
-48 / 8 ≤ t
-6 ≤ t
t ≥ -6
Hence, from the above,
We can conclude that the solution to the given inequality is t ≥ -6
The representation of the inequality in the number line is:

In Exercises 11–18, solve the inequality. Graph the solution.

Question 11.
-6t < 12
Answer:

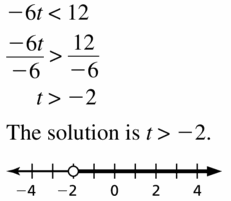
Question 12.
-9y > 9
Answer:
The given inequality is:
-9y > 9
y > -9 / 9
y > -1
Hence, from the above,
We can conclude that the solution to the given inequality is y > -1
The representation of the inequality in the number line is:

Question 13.
-10 ≥ -2z
Answer:

Question 14.
-15 ≤ -3c
Answer:
The given inequality is:
-15 ≤ -3c
15 ≤ 3c
15 / 3 ≤ c
5 ≤ c
c ≥ 5
Hence, from the above,
We can conclude that the solution to the given inequality is c ≥ 5
The representation of the inequality in the number line is:

Question 15.
\(\frac{n}{-3}\) ≥ 1
Answer:

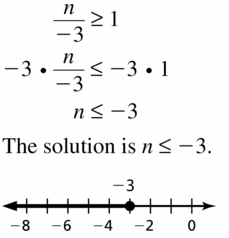
Question 16.
\(\frac{w}{-5}\) ≤ 16
Answer:
The given inequality is:
\(\frac{w}{-5}\) ≤ 16
w ≤ -16 ( 5 )
w ≤ -80
Hence, from the above,
We can conclude that the solution to the given inequality is w ≤ -80
The representation of the inequality in the number line is:

Question 17.
-8 < –\(\frac{1}{4}\)m
Answer:

Question 18.
-6y > –\(\frac{2}{3}\)
Answer:
The given inequality is:
-6 > –\(\frac{2}{3}\)y
6  > \(\frac{2}{3}\)y
6 ( 3 ) > 2y
18 > 2y
18 / 2 > y
9 > y
y < 9
Hence, from the above,
We can conclude that the solution to the given inequality is y < 9
The representation of the inequality in the number line is:

Question 19.
MODELING WITH MATHEMATICS
You have $12 to buy five goldfish for your new fish tank. Write and solve an inequality that represents the prices you can pay per fish.
Answer:

Question 20.
MODELING WITH MATHEMATICS
A weather forecaster predicts that the temperature in Antarctica will decrease by 8°F each hour for the next 6 hours. Write and solve an inequality to determine how many hours it will take for the temperature to drop at least 36°F.
Answer:
The inequality to determine the number of hours it will take for the temperature to drop at least 36° F is:
x ≥ 4.5

Explanation:
It is given that a weather forecaster predicts that the temperature in Antarctica will decrease by 8°F each hour for the next 6 hours.
Now,
Let the number of hours that will take to drop the temperature be x
So,
8x ≥ 36
x ≥ 36 / 8
x ≥ 4.5
Hence, from the above,
We can conclude that the inequality to determine the number of hours it will take for the temperature to drop at least 36° F is:
x ≥ 4.5 hours

USING TOOLS
In Exercises 21–26, solve the inequality. Use a graphing calculator to verify your answer.

Question 21.
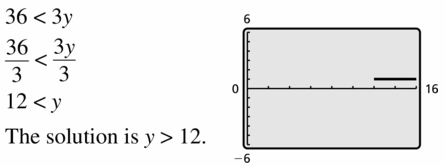
36 < 3y
Answer:

Question 22.
17v ≥ 51
Answer:
The given inequality is:
17v ≥ 51
v ≥ 51 / 17
v ≥ 3
Hence, from the above,
We can conclude that the solution to the given inequality is v ≥ 3
The representation of the inequality in the number line is:

Question 23.
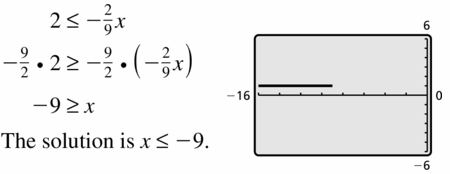
2 ≤ –\(\frac{2}{9}\)x
Answer:

Question 24.
4 > \(\frac{n}{-4}\)
Answer:
The given inequality is:
4 > \(\frac{n}{-4}\)
4 ( -4 ) > n
-16 > n
n < -16
Hence, from the above,
We can conclude that the solution to the given inequality is n < -16
The representation of the inequality in the number line is:

Question 25.
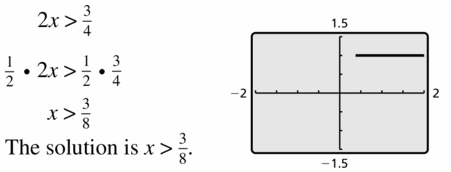
2x > \(\frac{3}{4}\)
Answer:

Question 26.
1.1y < 4.4
Answer:
The given inequality is:
1.1y < 4.4
\(\frac{11}{10}\)y > \(\frac{44}{10}\)
y > \(\frac{10 × 44}{11 × 10}\)
y > 4
Hence, from the above,
We can conclude that the solution to the given inequality is y > 4
The representation of the inequality in the number line is:

ERROR ANALYSIS
In Exercises 27 and 28, describe and correct the error in solving the inequality.

Question 27.

Answer:

Question 28.

Answer:
The given inequality is:
-4y ≤ -32
4y ≤ 32
y ≤ 32 /4
y ≤ 8
Hence, from the above,
We can conclude that the solution to the given inequality is:
y ≤ 8

Question 29.
ATTENDING TO PRECISION
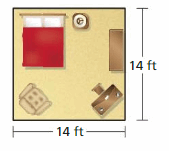
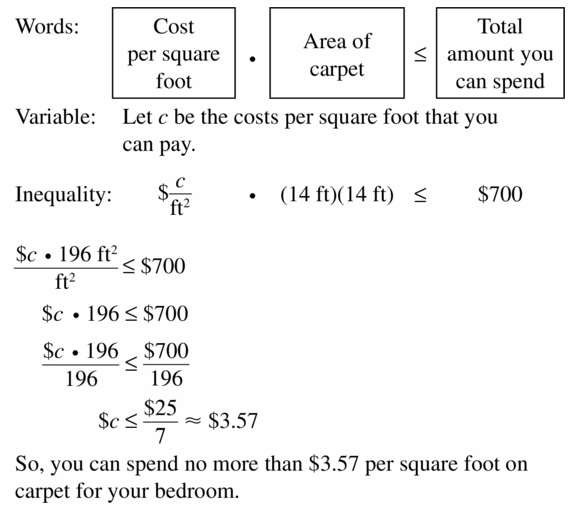
You have $700 to buy a new carpet for your bedroom. Write and solve an inequality that represents the costs per square foot that you can pay for the new carpet. Specify the units of measure in each step.

Answer:

Question 30.
HOW DO YOU SEE IT?
Let m > 0. Match each inequality with its graph. Explain your reasoning.

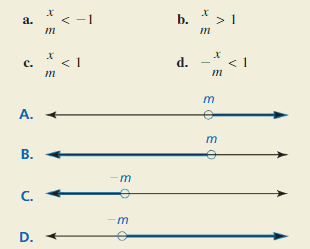
Answer:
The given inequalities are:
a. \(\frac{x}{m}\) < -1
b. \(\frac{x}{m}\) > 1
c. \(\frac{x}{m}\) < 1
d. –\(\frac{x}{m}\) < 1
It is given that m > 0 i.e., m is a positive number
Let,
The value of x is: 1
Now,
a.
The given inequality is:
\(\frac{x}{m}\) < -1
\(\frac{1}{m}\) < -1
1 < -m
-1 < m
m > -1
Hence,,
From the number lines, D) represents the required number line  for this inequality
b.
The given inequality is:
\(\frac{x}{m}\) > 1
x > m
1 > m
m < 1
Hence,
From the number lines, B) represents the required number line for this inequality
c.
The given inequality is:
\(\frac{x}{m}\) < 1
x < m
1 < m
m > 1
Hence,
From the number lines, A) represents the required number line for this inequality
d.
The given inequality is:
–\(\frac{x}{m}\) < 1
-x < -m
x < m
1 < m
m > 1
Hence,
From the number lines, A) represents the required number line for this inequality

Question 31.
MAKING AN ARGUMENT
You run for 2 hours at a speed no faster than 6.3 miles per hour.
a. Write and solve an inequality that represents the possible numbers of miles you run.
b. A marathon is approximately 26.2 miles. Your friend says that if you continue to run at this speed, you will not be able to complete a marathon in less than 4 hours. Is your friend correct? Explain.
Answer:

Question 32.
THOUGHT-PROVOKING
The inequality
\(\frac{x}{4}\) ≤ 5 has a solution of x = p. Write a second inequality that also has a solution of x = p.
Answer:
The second inequality that also has a solution x = p is:
x ≤ 20

Explanation:
The given inequality is:
\(\frac{x}{4}\) ≤ 5
It is given that the given inequality has a solution of x = p
So,
The second inequality that also has a second solution of x = p is:
\(\frac{x}{4}\) ≤ 5
x ≤ 5 ( 4 )
x ≤ 20
Hence, from the above,
We can conclude that the second inequality that also has a solution of x = p is:
x ≤ 20

Question 33.
PROBLEM-SOLVING
The U.S. Mint pays $0.02 to produce every penny. How many pennies are produced when the U.S. Mint pays more than $6 million in production costs?
Answer:

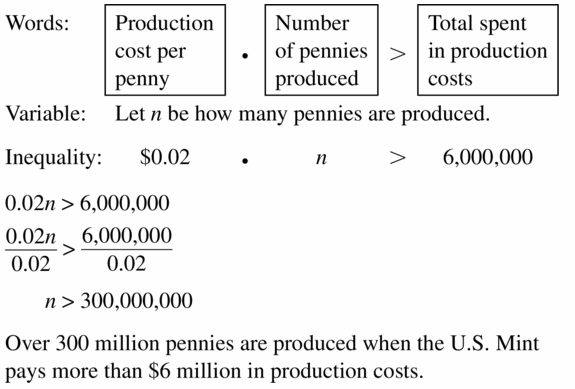
Question 34.
REASONING
Are x ≤ \(\frac{2}{3}\) and -3x ≤ -2 equivalent? Explain your reasoning.
Answer:
Yes,
x ≤ \(\frac{2}{3}\) and -3x ≤ -2 are equivalent

Explanation:
The given inequalities are -3x ≤ -2 and x ≤ \(\frac{2}{3}\)
Now,
x ≤ \(\frac{2}{3}\)
3x ≤ 2
Now,
-3x ≤ -2
Multiply with ‘-‘ on both sides
We know that,
– × – = +
So,
3x ≤ 2
Hence, from the above,
We can conclude that the given two inequalities are equivalent

Question 35.
ANALYZING RELATIONSHIPS
Consider the number line shown.

a. Write an inequality relating A and B.
b. Write an inequality relating -A and -B.
c. Use the results from parts (a) and (b) to explain why the direction of the inequality symbol must be reversed when multiplying or dividing each side of an inequality by the same negative number.
Answer:

Question 36.
REASONING
Why might solving the inequality \(\frac{4}{x}\) ≥ 2 by multiplying each side by x lead to an error? (Hint: Consider x > 0 and x < 0.)
Answer:
The given inequality is:
\(\frac{4}{x}\) ≥ 2
4 ≥ 2x
4 / 2 ≥ x
2 ≥ x
x ≤ 2
It is given that to consider x > 0 and x < 0 i.e., x as a positive number and a negative number
Now,
Multiply the given inequality by x on both sides and consider x as positive
4x ≥ 2x²
4x / 2 ≥ x²
2x / x ≥ x
2 ≥ x
x ≤ 2
Now,
Multiply the given inequality by x on both sides and consider x as negative
-4x ≥ -2x²
4x / 2 ≥ x²
2x ≥ x²
2x / x ≥ x
2 ≥ x
x ≤ 2
Hence, from the above,
We can conclude that there will be no error even when we multiply the given inequality with x on both sides

Question 37.
MATHEMATICAL CONNECTIONS
The radius of a circle is represented by the formula r = \(\frac{C}{2π}\). Write and solve an inequality that represents the possible circumferences C of the circle.

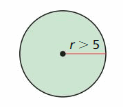
Answer:

Question 38.
CRITICAL THINKING
A water-skiing instructor recommends that a boat pulling a beginning skier has a speed less than 18 miles per hour. Write and solve an inequality that represents the possible distances d (in miles) that a beginner can travel in 45 minutes of practice time.
Answer:
The inequality that represents the possible distances that a beginner can travel in 45 minutes of practice time is:
d < 13.5 miles

Explanation:
It is given that a water-skiing instructor recommends that a boat pulling a beginning skier has a speed less than 18 miles per hour
The given speed is in terms of miles per hour
So,
The time should also be in hours
But the given time is in minutes
So,
We know that,
60 minutes = 1 hour
So,
45 minutes = \(\frac{45}{60}\) hours
= \(\frac{3}{4}\) hours
It is also given that the distance is d
We know that,
Speed = \(\frac{Distance}{Time}\)
So,
Distance = Speed × Time
Hence,
The inequality that represents the possible distances that a beginner can travel in 45 minutes of practice time is:
d < 18 ( \(\frac{3}{4}\) )
d < \(\frac{18 × 3}{4}\)
d < \(\frac{54}{4}\)
d < \(\frac{27}{2}\)
d < 13.5 miles
Hence, from the above,
We can conclude that the inequality that represents the possible distances that a beginner can travel in 45 minutes of practice time is:
d < 13.5 miles

Question 39.
CRITICAL THINKING
A local zoo employs 36 people to take care of the animals each day. At most, 24 of the employees work full time. Write and solve an inequality that represents the fraction of employees who work part-time. Graph the solution. Maintaining Mathematical Proficiency Solve the equation. Check your solution. (Section 1.2 and Section 1.3)
Answer:

Question 40.
5x + 3 = 13
Answer:
The given equaltion is:
5x + 3 = 13
5x = 13 – 3
5x = 10
x = 10 / 2
x = 5
Hence, from the above,
We can conclude that the solution to the given equaltion is x = 5

Question 41.
\(\frac{1}{2}\)y – 8 = -10
Answer:

Question 42.
-3n + 2 = 2n – 3
Answer:
The given equation is:
-3n + 2 = 2n – 3
-3n – 2n = -3 – 2
-5n = -5
5n = 5
n = 5 / 5
n = 1
Hence, from the above,
We can conclud ethat the solution to the given equation is n = 1

Question 43.
\(\frac{1}{2}\)z + 4 = \(\frac{5}{2}\)z – 8 Tell which number is greater.
Answer:

Question 44.
0.8, 85%
Answer:
The relation between the given numbers are:
0.8 < 85%

Explanation:
The given numbers are: 0.8 and 85%
We know that,
x% = \(\frac{x}{100}\)
We can rewrite 0.8 as 0.80 since both 0.8 and 0.80 are the same
So,
85% = \(\frac{85}{100}\)
0.8 = \(\frac{80}{100}\)
By comparison, we can get
0.8 is less than 85%
Hence, from the above,
We can conclude that
0.8 < 85%

Question 45.
\(\frac{16}{30}\), 50%
Answer:

Question 46.
120%, 0.12
Answer:
The relation between the given numbers are:
120% > 0.12

Explanation:
The given numbers are: 120% and 0.12
We know that,
x% = \(\frac{x}{100}\)
Now,
120% = \(\frac{120}{100}\)
0.12 = \(\frac{12}{100}\)
By comparison, we can get
120% is greater than 0.12
Hence, from the above,
We can conclude that
120% > 0.12

Question 47.
60%, \(\frac{2}{3}\)
Answer:

Lesson 2.4 Solving Multi-step Inequalities

Essential Question
How can you solve a multi-step inequality?

EXPLORATION 1
Solving a Multi-Step Inequality
Work with a partner.

• Use what you already know about solving equations and inequalities to solve each multi-step inequality. Justify each step.
• Match each inequality with its graph. Use a graphing calculator to check your answer.
a. 2x + 3 ≤ x + 5
b. -2x + 3 > x + 9
c. 27 ≥ 5x + 4x
d. -8x + 2x – 16 < -5x + 7x
e. 3(x – 3) – 5x > -3x – 6
f. -5x – 6x ≤ 8 – 8x – x


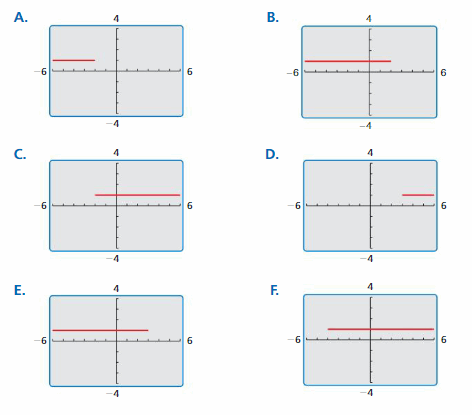
Answer:
The given inequalities are:
a. 2x + 3 ≤ x + 5
b. -2x + 3 > x + 9
c. 27 ≥ 5x + 4x
d. -8x + 2x – 16 < -5x + 7x
e. 3(x – 3) – 5x > -3x – 6
f. -5x – 6x ≤ 8 – 8x – x
The given graphing calculators are:

Now,
From the graphing calculators, we can observe that the graph is divided into 4 parts.
The first part indicates +x
The second part indicates -x
Now,
a.
The given inequality is:
2x + 3 ≤ x + 5
So,
2x – x ≤ 5 – 3
x ≤ 2
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 2
The graph B) matches the solution of the given inequality

b.
The given inequality is:
-2x + 3 > x + 9
So,
-2x – x > 9  -3
-3x > 6
x > -6 / 3
x > -2
Hence, from the above,
We can conclude that the solution to the given inequality is x > -2
The graph C) matches the solution of the given inequality

c.
The given inequality is:
27 ≥ 5x + 4x
So,
27 ≥ 9x
27 / 9 ≥ x
3 ≥ x
x ≤ 3
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 3
The graph E) matches the solution of the given inequality

d.
The given inequality is:
-8x + 2x – 16 < -5x + 7x
So,
-6x – 16 < 2x
-6x – 2x < 16
-8x < 16
x < -16 / 8
x < -2
Hence, from the above,
We can conclude that the solution to the given inequality is x < -2
Graph A) matches the solution of the given inequality

e.
The given inequality is:
3(x – 3) – 5x > -3x – 6
So,
3 ( x ) – 3 ( 3 ) – 5x > -3x – 6
3x – 9 – 5x > -3x – 6
-2x – 9 > -3x – 6
-2x + 3x > -6 + 9
x > 3
Hence, from the above,
We can conclude that the solution to the given inequality is x > 3
The graph D) matches the solution of the given inequality

f.
The given inequality is:
-5x – 6x ≥ 8 – 8x – x
So,
-11x ≥ 8 – 9x
-11x + 9x ≥ 8
-2x ≥ 8
x ≥ -8 / 2
x ≥ -4
Hence, from the above,
We can conclude that the solution to the given inequality is x ≥ -4
The graph F) matches the solution of the given inequality

Question 2.
How can you solve a multi-step inequality?
Answer:
The general procedure for solving multi-step inequality is as follows:
a) Clear parenthesis i.e., Brackets on both sides of the inequality and collect like terms
b) Addor subtract terms so the variable is on one side and the constant is on another side of the inequality sign

Question 3.
Write two different multi-step inequalities whose solutions are represented by the graph.

Answer:
The given graph is:

From the given graph,
We can observe that the marking started from -1 but by excluding -1 and continued till the left end of the graph
So,
The inequality represented by the graph is given as:
x < -1

2.4 Lesson

Monitoring Progress
Solve the inequality. Graph the solution.

Question 1.
4b – 1 < 7
Answer:
The given inequality is:
4b – 1 < 7
So,
4b < 7 + 1
4b < 8
b < 8 / 4
b < 2
Hence, from the above,
We can conclude that the solution to the given inequality is b < 2
The representation of the inequality in the number line is:

Question 2.
8 – 9c ≥ -28
Answer:
The given inequality is:
8 – 9c ≥ -28
-9c ≥ -28 – 8
-9c ≥ -36
9c ≥ 36
c ≥ 36 / 9
c ≥ 4
Hence, from the above,
We can conclude that the solution to the given inequality is c ≥ 4
The representation of the inequality in the number line is:

Question 3.
\(\frac{n}{-2}\) + 11 > 12
Answer:
The given inequality is:
\(\frac{n}{-2}\) + 11 > 12
\(\frac{n}{-2}\) > 12 – 11
\(\frac{n}{-2}\) > 1
n > 1 (-2)
n > -2
Hence, from the above,
We can conclude that the solution to the given inequality is n > -2
The representation of the inequality in the number line is:

Question 4.
6 ≥ 5 – \(\frac{v}{3}\)
Answer:
The given inequality is:
6 ≥ 5 – \(\frac{v}{3}\)
6 – 5 ≥ – \(\frac{v}{3}\)
-1 ≥ \(\frac{v}{3}\)
-3 ≥ v
v ≤ -3
Hence, from the above,
We can conclude that the solution to the given inequality is v ≤ -3
The representation of the inequality in the number line is:

Solve the inequality.

Question 5.
5x – 12 ≤ 3x – 4
Answer:
The given inequality is:
5x – 12 ≤ 3x – 4
5x – 3x ≤ 12 – 4
2x ≤ 8
x ≤ 8 / 2
x ≤ 4
Hence, from the above,
We can conclude that the solution to the given inequality is x ≤ 4

Question 6.
2(k – 5) < 2k + 5
Answer:
The given inequality is:
2 ( k – 5 ) < 2k + 5
So,
2 ( k ) – 2 ( 5 ) < 2k + 5
2k – 10 < 2k + 5
2k – 2k < 5 + 10
-10 < 5
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 7.
-4(3n – 1) > -12n + 5.2
Answer:
The given inequality is:
-4 ( 3n – 1 ) > -12n + 5.2
So,
-4 ( 3n ) – 4 ( -1 ) > -12n + 5.2
-12n + 4 > -12n + 5.2
-12n + 12n + 4 > 5.2
4 > 5.2
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 8.
3(2a – 1) ≥ 10a – 11
Answer:
The given inequality is:
3 ( 2a – 1 ) ≥ 10a – 11
So,
3 ( 2a ) – 3 ( 1 ) ≥ 10a – 11
6a – 3 ≥ 10a – 11
6a – 10a ≥ -11 + 3
-4a ≥ -8
4a ≥ 8
a ≥ 8 / 4
a ≥ 2
Hence, from the above,
We can conclude that the solution to the given inequality is a ≥ 2

Question 9.
WHAT IF?
You need a mean score of at least 85 points to advance to the next round. What scores in the fifth game will allow you to advance?
Answer:

Solving Multi-step Inequalities 2.4 Exercises

Vocabulary and Core Concept Check

Question 1.
WRITING
Compare solving multi-step inequalities and solving multi-step equations.
Answer:

Question 2.
WRITING
Without solving, how can you tell that the inequality 4x + 8 ≤ 4x – 3 has no solution?
Answer:
The given inequality is:
4x + 8  ≤ 4x – 3
Rearrange the variables ad constant terms
So,
4x – 4x ≤ -3 – 8
0 + 8 ≤ -3
8 ≤ -3
Hence, from the above,
We can observe that there is no variable x
Hence,
We can conclude that there is no solution for the given inequality

In Exercises 3–6, match the inequality with its graph.

Question 3.
7b – 4 ≤ 10
Answer:

Question 4.
4p + 4 ≥ 12
Answer:
The given inequality is:
4p + 4 ≥ 12
So,
4p ≥ 12 – 4
4p ≥ 8
p ≥ 8 / 4
p ≥ 2
Hence, from the above,
We can conclude that the solution to the given inequality is p ≥ 2
The graph represented for the solution is A) [ Se the graphs from Exercise 6 ]

Question 5.
-6g + 2 ≥ 20
Answer:

Question 6.
3(2 – f) ≤ 15

Answer:
The given inequality is:
3 (2 – f) ≤  15
So,
3 (2) – 3 (f) ≤  15
6 – 3f ≤  15
-3f ≤  15 – 6
-3f ≤  9
f ≤  -9 / 3
f ≤  -3
Hence, from the above,
We can conclude that the solution to the given inequality is f ≤  -3
The graph C) represents the solution of the given inequality

In Exercises 7–16, solve the inequality. Graph the solution.

Question 7.
2x – 3 > 7
Answer:

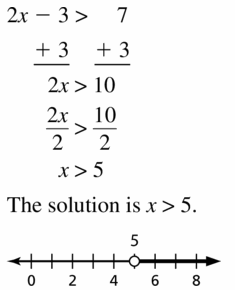
Question 8.
5y + 9 ≤ 4
Answer:
The given inequality is:
5y + 9 ≤ 4
So,
5y ≤  4  -9
5y ≤  -5
y ≤  -5 / 5
y ≤  -1
Hence, from the above,
We can conclude that the solution to the given inequality is y ≤  -1
The representation of the solution in the graph is:

Question 9.
-9 ≤ 7 – 8v
Answer:

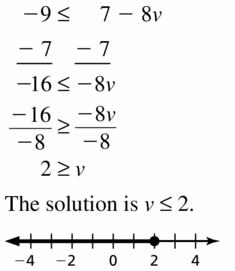
Question 10.
2 > -3t – 10
Answer:
The given inequality is:
2 > -3t – 10
So,
2 + 10 > -3t
12 > -3t
-12 / 3 > t
-4 > t
t < -4
Hence, from the above,
We can conclude that the solution to the given inequality is t < -4
The representation of the solution of the inequality in the graph is:

Question 11.
\(\frac{w}{2}\) + 4 > 5
Answer:

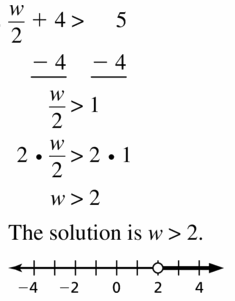
Question 12.
1 + \(\frac{m}{3}\) ≤ 6
Answer:
The given inequality is:
1 + \(\frac{m}{3}\) ≤ 6
So,
\(\frac{m}{3}\) ≤ 6 – 1
\(\frac{m}{3}\) ≤ 5
m ≤ 5 (3)
m ≤ 15
Hence, from the above,
We can conclude that the solution to the given inequality is m ≤ 15
The representation of the solution of the inequality in the graph is:

Question 13.
\(\frac{p}{-8}\) + 9 > 13
Answer:

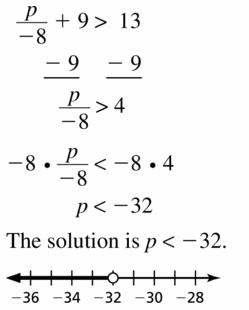
Question 14.
3 + \(\frac{r}{-4}\) ≤ 6
Answer:
The given inequality is:
3 + \(\frac{r}{-4}\) ≤ 6
\(\frac{r}{-4}\) ≤ 6 – 3
\(\frac{r}{-4}\) ≤ 3
r ≤ 3 (-4)
r ≤ -12
Hence, from the above,
We can conclude that the solution to the given inequality is r ≤ -12
The representation of the solution of the given inequality in the graph is:

Question 15.
6 ≥ -6(a + 2)
Answer:

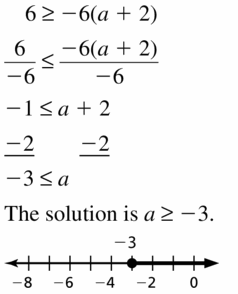
Question 16.
18 ≤ 3(b – 4)
Answer:
The given inequality is:
18 ≤ 3 (b – 4)
So,
18 ≤ 3 (b) – 3 (4)
18 ≤ 3b – 12
18 + 12 ≤ 3b
30 ≤ 3b
30 / 3 ≤ b
10 ≤ b
b ≥ 10
Hence, from the above,
We can conclude that the solution to the given inequality is b ≥ 10
The representation of the solution of the given inequality in the graph is:

In Exercises 17–28, solve the inequality.

Question 17.
4 – 2m > 7 – 3m
Answer:

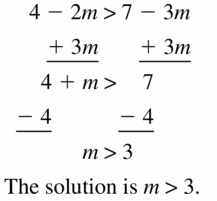
Question 18.
8n+ 2 ≤ 8n – 9
Answer:
The given nequality is:
8n + 2 ≤ 8n – 9
So,
8n – 8n + 2 ≤ -9
2 ≤ 9
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 19.
-2d – 2 < 3d + 8
Answer:

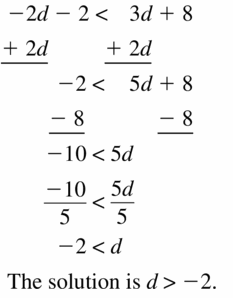
Question 20.
8 + 10f > 14 – 2f
Answer:
The given inequality is:
8 + 10f > 14 – 2f
10f + 2f > 14 – 8
12f > 6
f > 6 / 12
f > \(\frac{1}{2}\)
Hence, from the above,
We can conclude that the solution to the given inequality is f > \(\frac{1}{2}\)

Question 21.
8g – 5g – 4 ≤ -3 + 3g
Answer:

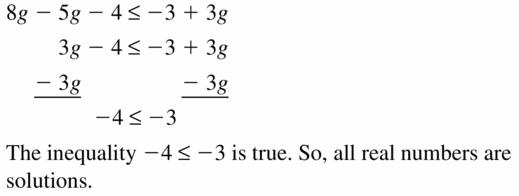
Question 22.
3w – 5 > 2w + w – 7
Answer:
The given inequality is:
3w – 5 > 2w + w – 7
So,
3w – 5 > 3w – 7
3w – 5 – 3w > -7
-5 > -7
5 > 7
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 23.
6(ℓ + 3) < 3(2ℓ + 6)
Answer:

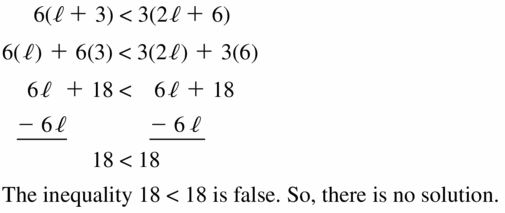
Question 24.
2(5c – 7) ≥ 10(c – 3)
Answer:
The given inequality is:
2 (5c – 7) ≥ 10 (c – 3)
So,
2 (5c) – 2 (7) ≥ 10 (c) – 10 (3)
10c – 14 ≥ 10c – 30
10c – 10c – 14 ≥ -30
-14 ≥ -30
14 ≥ 30
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 25.
4 (\(\frac{1}{2}\)t – 2 )> 2(t – 3)
Answer:

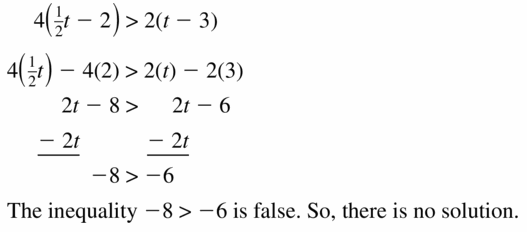
Question 26.
15 (\(\frac{1}{3}\)b + 3 ) ≤ 6(b + 9)
Answer:
The given inequality is:
15 ( (\(\frac{1}{3}\)b + 3 ) ) ≤ 6 (b + 9)
So,
15 ( (\(\frac{1}{3}\)b ) ) + 15 (3) ≤ 6 (b) + 6 (9)
5b + 45 ≤ 6b + 54
5b – 6b ≤ 54 – 45
-b ≤ 9
b ≤ -9
Hence, from the above,
We can conclude that the solution to the given inequality is b ≤ -9

Question 27.
9j – 6 + 6j ≥ 3(5j – 2)
Answer:

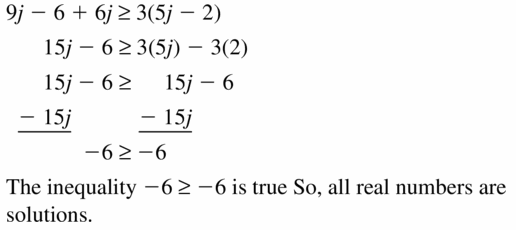
Question 28.
6h – 6 + 2h < 2(4h – 3)
Answer:
The given inequality is:
6h – 6 + 2h < 2 (4h – 3)
So,
8h – 6 < 2 (4h) – 2 (3)
8h – 6 < 8h – 6
8h – 8h < -6 + 6
0 < 0
Hence, from the above,
We can conclude that there is no solution for the given inequality

ERROR ANALYSIS
In Exercises 29 and 30, describe and correct the error in solving the inequality.

Question 29.

Answer:

Question 30.

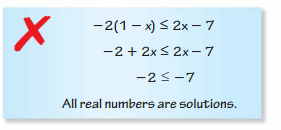
Answer:
The given inequality is:
-2 (1 – x) ≤ 2x – 7
-2 (1) + 2 (x) ≤ 2x – 7
-2 + 2x ≤ 2x – 7
-2 + 2x – 2x ≤ -7
-2 ≤ -7
2 ≤  7
Hence, from the above,
We can conclude that the given inequality has no solution

Question 31.
MODELING WITH MATHEMATICS
Write and solve an inequality that represents how many $20 bills you can withdraw from the account without going below the minimum balance.

Answer:

Question 32.
MODELING WITH MATHEMATICS
A woodworker wants to earn at least $25 an hour making and selling cabinets. He pays $125 for materials. Write and solve an inequality that represents how many hours the woodworker can spend building the cabinet.

Answer:
The inequality that represents the number of hours the woodworker can spend build the cabinet is:
x ≥ 5

Explanation:
It is given that a woodworker wants to earn at least $25 an hour making and selling cabinets. He pays $125 for materials.
Let x be the number of hours taken by the woodworker to build the cabinet
So,
The inequality that represents the number of hours the woodworker can spend build the cabinet is:
25 (x) ≥ 125
x ≥ 125 / 25
x ≥ 5
Hence, from the above,
We can conclude that the inequality that represents the number of hours the woodworker can spnd build the cabinet is x ≥ 5

Question 33.
MATHEMATICAL CONNECTIONS
The area of the rectangle is greater than 60 square feet. Write and solve an inequality to find the possible values of x.

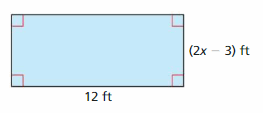
Answer:

Question 34.
MAKING AN ARGUMENT
Forest Park Campgrounds charges a $100 membership fee plus $35 per night. Woodland Campgrounds charges a $20 membership fee plus $55 per night. Your friend says that if you plan to camp for four or more nights, then you should choose Woodland Campgrounds. Is your friend correct? Explain.
Answer:
Yes, your friend is correct

Explanation:
It is given that the Forest Park Campgrounds charges a $100 membership fee plus $35 per night and the Woodland Campgrounds charges a $20 membership fee plus $55 per night.
It is also given that your friend says that if you plan to camp for four or more nights, then you should choose Woodland Campgrounds.
So,
Let x be the number of nights you spend
Now,
The charge of the Forest Park Campgrounds for x nights = 100 + 35x
The charge of the Woodland Campgrounds = 20 + 55x
Now,
It is given that for four or more nights i.e., x ≥ 4, you will choose Woodland Campgrounds
So,
We have to verify the above statement
So,
20 + 55x ≥ 100 + 35x
55x – 35x ≥ 100 – 20
20x ≥ 80
x ≥ 80 / 20
x ≥ 4
Hence, from the above,
We can conclude that your friend is correct.

Question 35.
PROBLEM-SOLVING
The height of one story of a building is about 10 feet. The bottom of the ladder on the truck must be at least 24 feet away from the building. How many stories can the ladder reach? Justify your answer.

Answer:

Question 36.
HOW DO YOU SEE IT?
The graph shows your budget and the total cost of x gallons of gasoline and a car wash. You want to determine the possible amounts (in gallons) of gasoline you can buy within your budget.
a. What is your budget?

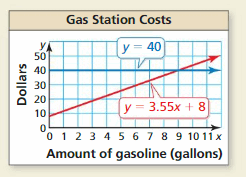
Answer:
Your budget is: $40

Explanation:
The given graph is:

From the graph,
We can observe that x-axis represents the amount of gasoline ( gallons ) and the y-axis represents the budget
From the graph,
The line is represented parallel to the x-axis i.e., Budget
So,
From the graph,
The given equation is:
y = 40
Hence, from the above,
We can conclude that the budget is: $40

b. How much does a gallon of gasoline cost? How much does a car wash cost?
Answer:
The cost of a gallon of gasoline is: $3.55
The cost of a car wash is: $8

Explanation:
It is given that the graph shows your budget and the total cost of x gallons of gasoline and a car wash.
From the graph,
We know that,
The x-axis represents the amount of gasoline ( gallons )
So,
The equation represented by the x-axis is:
y = 3.55x + 8
So,
From the equation,
We know that,
The coefficient of x represents the cost of x gallons of gasoline and the constant term represents the cost of a car wash
Hence, from the above,
We can conclude that
The cost of a gallon of gasoline is: $3.55
The cost of a car wash is: $8

c. Write an inequality that represents the possible amounts of gasoline you can buy.
Answer:
The inequality that represents the possible amounts of gasoline you can buy is:
x ≤ 9 gallons

Explanation:
From the graph,
We know that,
The x-axis represents the amounts of gasoline you can buy
We know that,
y = 3.55x + 8
We know that,
The budget will be less than or equal to $40
So,
3.55x + 8 ≤ 40
3.55x ≤ 40 – 8
3.55x ≤ 32
x ≤ 32 / 3.55
x ≤ 9 [ Approx. ]
Hence, from the above,
We can conclude that the inequality that represents the possible amounts of gasoline you can buy is:
x ≤ 9

d. Use the graph to estimate the solution of your inequality in part (c).
Answer:
From part (c),
The required inequality is:
3.55x + 8 ≤ 40
From the graph,
We can observe the x-axis and y-axis intersected at one particular point.
The particular point is the estimated solution of the inequality
So,
The particular point = (x , y ) = ( 9 , 40 )
Hence, from the above,
We can conclude that the estimated solution of your inequality in part (c) is ( 9, 40 )

Question 37.
PROBLEM-SOLVING
For what r values of r will the area of the shaded region be greater than or equal to 9(π – 2)?
Answer:

Question 38.
THOUGHT-PROVOKING
A runner’s times (in minutes) in the four races he has completed are 25.5, 24.3, 24.8, and 23.5. The runner plans to run at least one more race and wants to have an average time of less than 24 minutes. Write and solve an inequality to show how the runner can achieve his goal.
Answer:
The inequality that shows the runner can achieve his goal is:
x < 21.9 minutes

Explanation:
It is given that a runner’s times (in minutes) in the four races he has completed are 25.5, 24.3, 24.8, and 23.5.
It is also given that the runner plans to run at least one more race and wants to have an average time of less than 24 minutes.
Now,
Let x be the time in the fifth race [ Since it is given that the runner plans to run at least one more race ]
We know that,
Average = \(\frac{The sum of all the items}{The number of items}\)
Now,
Average = \(\frac{25.5 + 24.3 + 24.8 + 23.5 + x}{5}\)
Average = \(\frac{98.1 + x}{5}\)
It is given that the average time will be less than 24 minutes
So,
\(\frac{98.1 + x}{5}\) < 24
98.1 + x < 24 (5)
98.1 + x < 120
x < 120 – 98.1
x < 21.9 minutes
Hence, from the above,
We can conclude that the inequality that shows the runner can achieve his goal is x < 21.9 minutes

REASONING
In Exercises 39 and 40, find the value of a for which the solution of the inequality is all real numbers.

Question 39.
a(x + 3) < 5x + 15 – x
Answer:

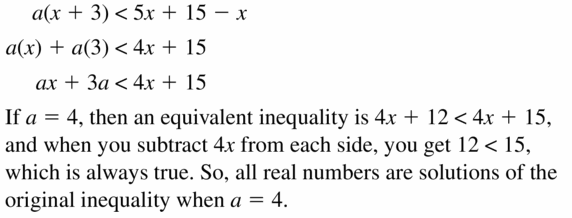
Question 40.
3x + 8 + 2ax ≥ 3ax – 4a
Answer:
The value of a is: 3

Explanation:
The given inequality is:
3x + 8 + 2ax ≥ 3ax – 4a
So,
3x + 2ax – 3ax ≥ -4a – 8
3x – ax ≥ -4a – 8
It is given that the solution of the given inequality is all real numbers
So,
x = 0
So,
To make x = 0,
We can observe from the inequality that ‘a’ must be equal to 3
Hence, from the above,
We can conclude that the value of a is: 3

Maintaining Mathematical Proficiency
Write the sentence as an inequality. (Section 2.1)

Question 41.
Six times a number y is less than or equal to 10.
Answer:

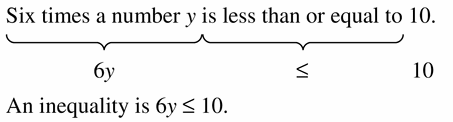
Question 42.
A number p plus 7 is greater than 24.
Answer:
The given worded form is:
A number p plus 7 is greater than 24
Hence,
The representation of the worded form in the form of inequality is:
p + 7 > 24

Question 43.
The quotient of a number r and 7 is no more than 18.
Answer:

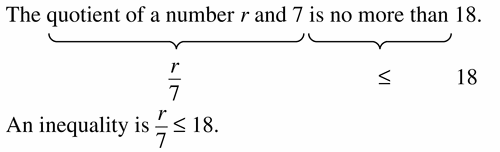
Solving Linear Inequalities Study Skills: Analyzing Your Errors

2.1–2.4 What Did You Learn?

Core Vocabulary

Core Concepts
Section 2.1
Representing Linear Inequalities, p. 57

Section 2.2

Section 2.3
Multiplication and Division Properties of Inequality (c > 0), p. 68
Multiplication and Division Properties of Inequality (c < 0), p. 69

Section 2.4
Solving Multi-Step Inequalities, p. 74
Special Solutions of Linear Inequalities, p. 75

Mathematical Practices

Question 1.
Explain the meaning of the inequality symbol in your answer to Exercise 47 on page 59. How did you know which symbol to use?
Answer:
In Exercise 47 on page 59,
The inequality symbol we used is: ≤
The meaning of ≤ is ” Less than or equal to ”
In Exercise 47,
It is given that the Xianren bridge arch is the longest natural arch with a length of 400 feet i.e., there is no arch longer than the Xianren bridge arch and the remaining natural arches are shorter than the Xianren arch
Hence,
The lengths of all the arches including the Xianren arch will be represented by the inequality symbol “≤”

Question 2.
In Exercise 30 on page 66, why is it important to check the reasonableness of your answer in part (a) before answering part (b)?
Answer:
In part (a), it is given that you have to beat your competitor with your score.
So,
Your score must be greater than your competitor
Then only you can solve part (b).

Question 3.
Explain how considering the units involved in Exercise 29 on page 71 helped you answer the question.
Answer:
In Exercise 29 on page 71,
The mat that is given is in the form of the square since its length and width both are the same
So,
We know that,
Area of the square = Side²
Let the cost per square foot be x
So,
The inequality formed will be like:
( Area of the square ) ⋅ x ≤ $700

Study Skills

Analyzing Your Errors

Application Errors
What Happens: You can do numerical problems, but you struggle with problems that have context.
How to Avoid This Error: Do not just mimic the steps of solving an application problem. Explain out loud what the question is asking and why you are doing each step. After solving the problem, ask yourself, “Does my solution make sense?”

Solving Linear Inequalities Maintaining 2.1 – 2.4 Quiz

Write the sentence as an inequality. (Section 2.1)

Question 1.
A number z minus 6 is greater than or equal to 11.
Answer:
The given worded form is:
A number z minus 6 is greater than or equal to 11
Hence,
The representation of the worded form in the form of inequality is:
z – 6 ≥ 11

Question 2.
Twelve is no more than the sum of -1.5 times a number w and 4.
Answer:
The given worded form is:
Twelve is no more than the sum of -1.5 times a number w and 4
Hence,
The representation of the worded form in the form of inequality is:
12 ≤ -1.5w + 4

Write an inequality that represents the graph.(Section 2.1)

Question 3.

Answer:
The inequality that represents the given graph is:
x < 0

Explanation:
The given graph is:

From the above number line,
We can observe that the marked line started from 0 that excludes 0 and continued till the left end of the number line
Hence,
The inequality that represents the given graph is:
x < 0

Question 4.

Answer:
The inequality that represents the given graph is:
x ≥ 8

Explanation:
The given graph is:

From the above graph,
The marked line started from 8 that includes 8 and continued till the right end of the number line.
Hence,
The inequality that represents the given graph is:
x ≥ 8

Solve the inequality. Graph the solution. (Section 2.2 and Section 2.3)

Question 5.
9 + q ≤ 15
Answer:
The solution to the given inequality is:
q ≤ 6

Explanation:
The given inequality is:
9 + q ≤ 15
So,
q ≤ 15 – 9
q ≤ 6
Hence, from the above,
We can conclude that the solution to the given inequality is q ≤ 6
The representation of the solution of the inequality in the graph is:

Question 6.
z – (-7) < 5
Answer:
The solution to the given inequality is:
z < -2

Explanation:
The given inequality is:
z – (-7) < 5
So,
z + 7  < 5
z < 5 – 7
z < -2
Hence, from the above,
We can conclude that the solution to the given inequality is z < -2
The representation of the solution of the inequality in the graph is:

Question 7.
-3 < y – 4
Answer:
The solution to the given inequality is:
y > 1

Explanation:
The given inequality is:
-3 < y – 4
So,
-3 + 4 < y
1 < y
y > 1
Hence, from the above,
We can conclude that the solution to the given inequality is y > 1
The representation of the solution of inequality in the graph is:

Question 8.
3p ≥ 18
Answer:
The solution to the given inequality is:
p ≥ 6

Explanation:
The given inequality is:
3p ≥ 18
p ≥ 18 / 3
p ≥ 6
Hence, from the above,
We can conclude that the solution to the given inequality is p ≥ 6
The representation of the solution of the inequality in the graph is:

Question 9.
6 > \(\frac{w}{-2}\)
Answer:
The solution to the given inequality is:
w < -12

Explanation:
The given inequality is:
6 > \(\frac{w}{-2}\)
So,
6 (-2) > w
-12 > w
w < -12
Hence, from the above,
We can conclude that the solution to the given inequality is w < -12
The representation of the solution of the inequality in the graph is:

Question 10.
-20x > 5
Answer:
The solution to the given inequality is:
x > – \(\frac{1}{4}\)
So,
x > -0.25

Explanation:
The given inequality is:
-20x > 5
So,
x > -5 / 20
x > – \(\frac{1}{4}\)
Hence, from the above,
We can conclude that the solution to the given inequality is x > –\(\frac{1}{4}\)
The representation of the solution of the inequality in the graph is:

Solve the inequality. (Section 2.4)

Question 11.
3y – 7 ≥ 17
Answer:
The solution to the given inequality is:
y ≥ 8

Explanation:
The given inequality is:
3y – 7 ≥ 17
So,
3y ≥ 17 + 7
3y ≥ 24
y ≥ 24 / 3
y ≥ 8
Hence, from the above,
We can conclude that the solution to the given inequality is y ≥ 8

Question 12.
8(3g – 2) ≤ 12(2g + 1)
Answer:
There is no soution for the given inequality

Explanation:
The given inequality is:
8 (3g – 2) ≤ 12 (2g + 1)
So,
8 (3g) – 8 (2) ≤ 12 (2g) + 12 (1)
24g – 16 ≤ 24g + 12
24g – 24g – 16 ≤ 12
-16 ≤ 12
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 13.
6(2x – 1) ≥ 3(4x + 1)
Answer:
There is no solution for the given inequality

Explanation:
The given inequality is:
6 (2x – 1)≥ 3 (4x + 1)
So,
6 (2x) – 6 (1) ≥ 3 (4x) + 3 (1)
12x – 6 ≤ 12x + 3
12x – 6 – 12x ≤ 3
-6 ≤ 3
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 14.
Three requirements for a lifeguard training course are shown. (Section 2.1)
a. Write and graph three inequalities that represent the requirements.
b. You can swim 250 feet, tread water for 6 minutes, and swim 35 feet underwater without taking a breath. Do you satisfy the requirements of the course? Explain.

Answer:
a.
The given requirements are:
1. Swim at least 100 yards
2. Tread water for at least 5 minutes
3. Swim 10 yards or more underwater without taking a breath
Now,
1.
The inequality that represents the first requirement is:
x ≥ 100 yards
2.
The inequality that represents the second requirement is:
x ≥ 5 minutes
3.
The inequality that represents the third requirement is:
x ≥ 10 yards

b.
It is given that you can swim 250 feet, tread water for 6 minutes, and swim 35 feet underwater without taking a breath.
From part (a),
The inequalities for the three requirements are:
x ≥ 100 yards
x ≥ 5 minutes
x ≥ 10 yards
Hence, from the above,
We can conclude that you satisfied the requirements of the course

Question 15.
The maximum volume of an American white pelican’s bill is about 700 cubic inches. A pelican scoops up 100 cubic inches of water. Write and solve an inequality that represents the additional volumes the pelican’s bill can contain. (Section 2.2)
Answer:
The inequality that represents the additional volumes of the pelican’s bill can contain is:
x  ≤ 600

Explanation:
It is given that the maximum volume of an American white pelican’s bill is about700 cubic inches. A pelican scoops up 100 cubic inches of water.
Let x be the additional volumes the pelican’s bill can contain
It is also given that the maximum volume is 700 cubic inches and a pelican’s bill scoops up 100 cubic inches of water
Hence,
The inequality that represents the additional volumes of the pelican’s bill can contain is:
x + 100 ≤ 700
x ≤ 700 – 100
x ≤ 600

Question 16.
You save $15 per week to purchase one of the bikes shown. (Section 2.3and Section 2.4)
a. Write and solve an inequality to find the numbers of weeks you need to save to purchase a bike.
b. Your parents give you $65 to help you buy the new bike. How does this affect your answer in part (a)? Use an inequality to justify your answer.

Answer:
a.
It is given that you save $15 per week to purchase one of the bikes
From the fig,
It is given that the starting price of the bike is $120
Now,
Let x be the number of weeks
Hence,
The inequality that representing the number of weeks you need to save to purchase a bike is:
15 ⋅ x ≥ 120
15x ≥ 120
x ≥ 120 / 15
x ≥ 8
Hence, from the above,
We can conclude that the number of weeks you need to save to purchase a bike is 8 weeks

b.
It is given that your parents give you $65 to help you buy the new bike.
We know that,
The starting price of the bike is: $120
So,
The remaining amount that needs to purchase a bike = 120 – 65
= $55

Lesson 2.5 Solving Compound Inequalities

Essential Question
How can you use inequalities to describe intervals on the real number line?
EXPLORATION 1
Describing Intervals on the Real Number
Work with a partner.
In parts (a)–(d), use two inequalities to describe the interval.

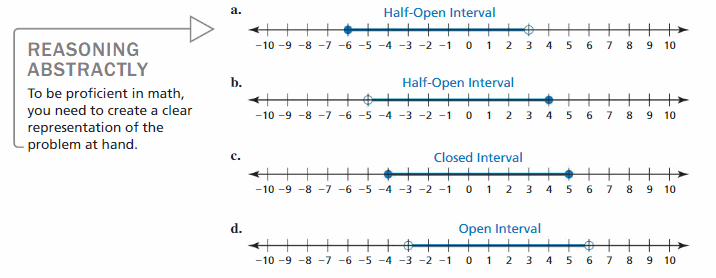
e. Do you use “and” or “or” to connect the two inequalities in parts (a)–(d)? Explain.
Answer:
(a) – (d):
The given graphs are:

From the given graphs,
We can observe that the marked lines are from a certain number to a certain number
Now,
a.
In the given graph,
The marked line starting from -3 excluding -3 and continued till -6 including -6
So,
The inequality that represents the given interval is:
x ≥ -6 and x < -3
Hence,
The compound inequality that represents the given interval is:
-6 ≤ x < -3

b.
In the given graph,
The marked line starting from -5 excluding -5 and continued till 4 including 4
So,
The inequality that represents the given interval is:
x > -5 and x < 4
Hence,
The compound inequality that represents the given interval is:
-5 < x < 4

c.
In the given graph,
The marked line starting from -4 including -4 and continued till 5 including 5
So,
The inequality that represents the given interval is:
x ≥ -4 and x ≤ 5
Hence,
The compound inequality that represents the given interval is:
-4 ≤ x ≤ 5

d.
In the given graph,
The marked line starting from -3 excluding -3 and continued till 6 including 6
So,
The inequality that represents the given interval is:
x > -3 and x < 6
Hence,
The compound inequality that represents the given interval is:
-3 < x < 6

e.
We use “and” to connect the two inequalities in parts (a) – (d)
Now,
From (a) – (d),
We can observe that,
For Half-open interval,
We use ≥ and <
For closed interval,
We use ≥ and ≤
For open interval,
We use > and <

EXPLORATION 2
Describing Two Infinite Intervals
Work with a partner. In parts (a)–(d), use two inequalities to describe the interval.

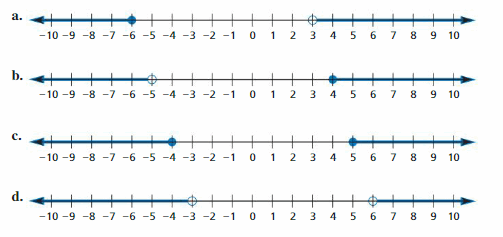
e. Do you use “and” or “or” to connect the two inequalities in parts (a)–(d)? Explain.
Answer:
The given graphs are:

(a) – (d):
a.
In the given graph,
The first marked line starting from -6 including -6 and continued till the end of the left side of the graph
The second marked line starting from 3 excluding 3 and continued till the end of the right side of the graph
So,
The inequality that represents the given intervals are:
x ≤ -6 and x > 3
Hence,
The compound inequality that represents the given interval is:
-6 ≤ x > 3

b.
In the given graph,
The first marked line starting from -5 excluding -5 and continued till the end of the left side of the graph
The second marked line starting from 4 including 4 and continued till the end of the right side of the graph
So,
The inequality that represents the given intervals are:
x < -5 and x ≥ 4
Hence,
The compound inequality that represents the given interval is:
-5 < x ≥ 4

c.
In the given graph,
The first marked line starting from -4 including -4 and continued till the end of the left side of the graph
The second marked line starting from 5 including 5 and continued till the end of the right side of the graph
So,
The inequality that represents the given intervals are:
x ≤ -4 and x ≥ 5
Hence,
The compound inequality that represents the given interval is:
-4 ≤ x ≥ 5

d.
In the given graph,
The first marked line starting from -3 excluding -3 and continued till the end of the left side of the graph
The second marked line starting from 6 excluding 6 and continued till the end of the right side of the graph
So,
The inequality that represents the given intervals are:
x < -3 and x > 6
Hence,
The compound inequality that represents the given interval is:
-3 < x > 6

e.
We use “and” to connect the two inequalities in parts (a) – (d)
Now,
From (a) – (d),
We can observe that,
For Half-open interval,
We use ≥ and <
For closed interval,
We use ≥ and ≤
For open interval,
We use > and <

Communicate Your Answer

Question 3.
How can you use inequalities to describe intervals on the real number line?
Answer:
An inequality that includes the boundary point indicated by the “or equal” part of the symbols ≤ and ≥ with a closed dot on the number line. The symbol (∞) indicates the interval is unbounded to the right. Express ordering relationships using the symbol < for “less than” and > for “greater than.”

2.5 Lesson

Monitoring Progress

Write the sentence as an inequality. Graph the inequality.

Question 1.
A number d is more than 0 and less than 10.
Answer:
The given worded form is:
A number d is more than 0 and less than 10
Hence,
The representation of the given worded form in the form of inequality is:
d > 0 and d < 10
The representation of the inequalities in the form of compound inequality is:
0 < d < 10
The representation of the compound inequality in the graph is:

Question 2.
A number a is fewer than -6 or no less than -3.
Answer:
The given worded form is:
A number a is fewer than -6 or no less than -3
Hence,
The representation of the given worded form in the form of inequality is:
a < -6 or a > -3
The representation of the inequalities in the graph is:

Solve the inequality. Graph the solution.

Question 3.
5 ≤ m + 4 < 10
Answer:
The given inequality is:
5 ≤ m + 4 < 10
Subtract by 4 on both sides
5 – 4 ≤ m + 4 – 4 < 10 – 4
1 ≤ m < 6
Hence, from the above,
We can conclude that the compound inequality for the given inequality is: 1 ≤ m < 6
The representation of the compound inequality in the graph is:

Question 4.
-3 < 2k – 5 < 7
Answer:
The given inequality is:
-3 < 2k – 5 < 7
Add 5 on both sides
-3 + 5 < 2k – 5 + 5 < 7 + 5
2 < 2k < 12
Divide by 2 on both sides
1 < k < 6
Hence, from the avove,
We can conclude that the compound inequality for the given inequality is: 1 < k < 6
The representation of the compound inequality in the graph is:

Question 5.
4c + 3 ≤ -5 or c – 8 > -1
Answer:
The given inequality is:
4c + 3 ≤ -5 or c – 8 > -1
So,
4c ≤ -5 – 3 or c > -1 + 8
4c ≤ -8 or c > 7
c ≤ -8 / 4 or c > 7
c ≤ -2 or c > 7
Hence, from the above,
We can conclude that the solutions to the given inequality are: c ≤ -2 or c > 7
The representations of the solutions in the graph are:

Question 6.
2p + 1 < -7 or 3 – 2p ≤ -1
Answer:
The given inequality is:
2p + 1 < -7 or 3 – 2p ≤ -1
So,
2p < -7 – 1 or -2p ≤ -1 – 3
2p < -8 or -2p ≤ -4
p < -8 / 2 or p ≤ -4 / (-2)
p < -4 or p ≤ 2
Hence, from the above,
We can conclude that the solutions to the given inequality are: p < -4 or p ≤ 2
The representations of the solutions in the graph are:

Question 7.
Write and solve a compound inequality that represents the temperature rating (in degrees Fahrenheit) of the winter boots.

Answer:
The range of the temperature rating ( In °C ) of the winter boots is: -40°C to 15°C
We know that,
°F = ( °C × \(\frac{9}{5}\) ) + 32
Now,
To convert -40°C into °F,
°F = ( -40°C × \(\frac{9}{5}\) ) + 32
°F = -72 + 32
°F = – 40°F
Now,
To convert 15°C into °F,
°F = ( 15 × \(\frac{9}{5}\) ) + 32
°F = 27 + 32
°F = 59°F
Let t be the temperature in °F
So,
The representation of the temperature ranges in the form of inequalities is:
t > -40°F and t < 59°F
Hence,
The representation of the temperature ranges in the form of compound inequality is:
-40°F < t < 59°F

Solving Compound Inequalities 2.5 Exercises

Vocabulary and Core Concept Check

Question 1.
WRITING
Compare the graph of -6 ≤ x ≤ -4 with the graph of x ≤ -6 or x ≥ -4.
Answer:

Question 2.
WHICH ONE do DOESN’T BELONG?
Which compound inequality does not belong with the other three? Explain your reasoning.

Answer:
The given inequalities are:
a. a > 4 or a < -3
b. a< -2 or a > 8
c. a > 7 or a < -5
d. a < 6 or a > -9
Now,
Represent all the inequalities in the graph
So,
a.
The given inequality is:
a > 4 or a < -3
The representation of the inequalities in the graph is:

b.
The given inequality is:
a < -2 or a > 8
The representation of the inequalities in the graph is:

c.
The given inequality is:
a > 7 or a < -5
The representation of the inequalities in the graph is:

d.
The given inequality is:
a < 6  or a > -9
The representation of the inequalities in the graph is:

From the above,
We can conclude that inequality c) does not belong with the other three inequalities

In Exercises 3–6, write a compound inequality that is represented by the graph.

Question 3.

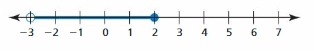
Answer:

Question 4.

Answer:
The given graph is:

From the above graph,
We can observe that the marked line started from 7 excluding 7 and continued till 14 excluding 14
Hence,
The representation of the inequalities from the given graph is:
x > 7 and x < 14
The representation of the inequalities in the form of compound inequality is:
7 < x < 14

Question 5.

Answer:

Question 6.

Answer:
The given graph is:

From the above graph,
We can observe that
The first marked line started from 4 including 4 and continued till the end of the left end of the graph
The second marked line started from 6 excluding 6 and continued till the end of the right end of the graph
Hence,
The representation of the given graph in the form of inequality is:
x ≤ 4 or x > 6

In Exercises 7–10, write the sentence as an inequality. Graph the inequality.

Question 7.
A number p is less than 6 and greater than 2.
Answer:

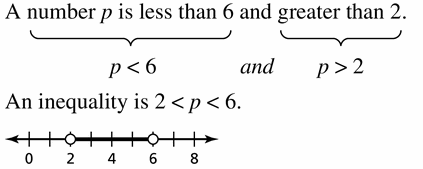
Question 8.
A number n is less than or equal to -7 or greater than 12.
Answer:
The given worded form is:
A number n is less than or equal to -7 or greater than 12
Hence,
The representation of the given worded form in the form of inequality is:
n ≤ -7 or n > 12
The representation of the inequalities in the graph is:

Question 9.
A number m is more than -7\(\frac{2}{3}\) or at most -10.
Answer:

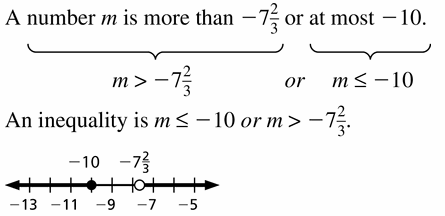
Question 10.
A number r is no less than -1.5 and fewer than 9.5.
Answer:
The given worded form is:
A number r is no less than -1.5 and fewer than 9.5
Hence,
The representation of the given worded form in the form of inequality is:
r > -1.5 and r < 9.5
Hence,
The representation of the given worded form in the form of compound inequality is:
-1.5 < r < 9.5
The representation of the compound inequality in the graph is:

Question 11.
MODELING WITH MATHEMATICS
Slitsnails are large mollusks that live in deep waters. They have been found in the range of elevations shown. Write and graph a compound inequality that represents this range.

Answer:

Question 12.
MODELING WITH MATHEMATICS
The life zones on Mount Rainier, a mountain in Washington, can be approximately classified by elevation, as follows.
Low-elevation forest: above 1700 feet to 2500 feet mid-elevation forest: above 2500 feet to 4000 feet Subalpine: above 4000 feet to 6500 feet
Alpine: above 6500 feet to the summit

Write a compound inequality that represents the elevation range for each type of plant life.
a. trees in the low-elevation forest zone
b. flowers in the subalpine and alpine zones
Answer:
It is given that the elevations of the life zones on Mount Rainier are as follows:
Low-elevation forest: above 1700 feet to 2500 feet
Mid-elevation forest: above 2500 feet to 4000 feet
Subalpine: above 4000 feet to 6500 feet
Alpine: above 6500 feet to the summit
Let the elevation range for each type of plant life be x
So,
a.
The inequality that represents the elevation range of trees in the low-elevation forest zone is:
x > 1700 feet and x < 2500 feet
Hence,
The representation of the elevation range of trees in the low-elevation forest zone in the form of compound inequality is:
1700 feet < x < 2500 feet
b.
The inequalities that represent the elevation range of trees in the subalpine and alpine zones is:
Subalpine zone: x > 4000 feet and x < 6500 feet
Alpine zone: x > 6500 feet
Hence,
The representation of the elevation range of trees in the Subalpine zone and Alpine zone in the form of compound inequality is:
Subalpine zone: 4000 feet < x < 6500 feet
Alpine zone: x > 6500 feet

In Exercises 13–20, solve the inequality. Graph the solution.

Question 13.
6 < x + 5 ≤ 11
Answer:

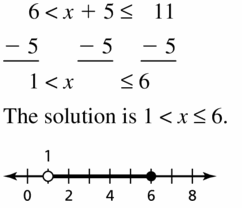
Question 14.
24 > -3r ≥ -9
Answer:
The given inequality is:
24 > -3r ≥ -9
Divide by 3 on both sides
( 24 / 3 ) > ( -3r / 3 ) ≥ ( -9 / 3 )
8 > -r ≥ -3
Multiply with ‘-‘ on both sides
-8 < r ≤ 3 [ Because when we multiply with ‘-‘, we have to change the inequality signs also ]
Hence,
The representation of the solution of the given inequality in the graph is:

Question 15.
v + 8 < 3 or -8v < -40
Answer:

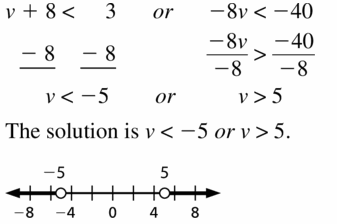
Question 16.
-14 > w + 3 or 3w ≥ -27
Answer:
The given inequality is:
-14 > w + 3 or 3w ≥ -27
So,
-14 – 3 > w or w ≥ -27 / 3
-17 > w or w ≥ -9
w < -17 or w ≥ -9
Hence,
The representation of the solutions of the given inequality in the graph is:

Question 17.
2r + 3 < 7 or -r + 9 ≤ 2
Answer:

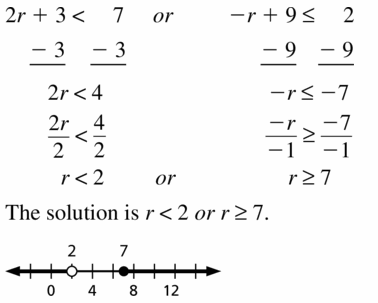
Question 18.
-6 < 3n + 9 < 21
Answer:
The given inequality is:
-6 < 3n + 9 < 21
Subtract with 9 on both sides
-6 – 9 < 3n + 9 – 9 < 21 – 9
-15 < 3n < 12
Divide by 3 on both sides
( -15 / 3 ) < ( 3n / 3 ) < ( 12 / 3 )
-5 < n < 4
Hence,
The representation of the solution of the inequality in the graph is:

Question 19.
-12 < \(\frac{1}{2}\)(4x + 16) < 18
Answer:

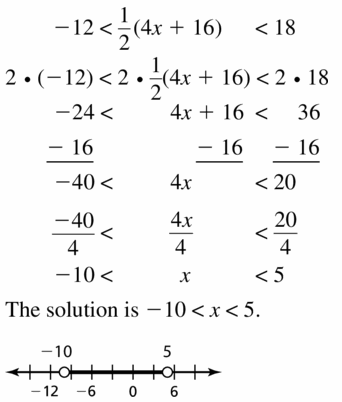
Question 20.
35 < 7(2 – b) or \(\frac{1}{3}\)(15b – 12) ≥ 21
Answer:
The given inequality is:
35 < 7 (2 – b) or \(\frac{1}{3}\) ( 15b – 12 ) ≥ 21
So,
35 < 7 (2) – 7 (b) or 15b – 12 ≥ 21 (3)
35 < 14 – 7b or 15b – 12 ≥ 63
7b < 14 – 35 or 15b ≥ 63 + 12
7b < -21 or 15b ≥ 75
b < -21 / 7 or b ≥ 75 / 15
b < -3 or b ≥ 5
Hence,
The representation of the solutions of the given inequality in the graph is:

ERROR ANALYSIS
In Exercises 21 and 22, describe and correct the error in solving the inequality or graphing the solution.

Question 21.

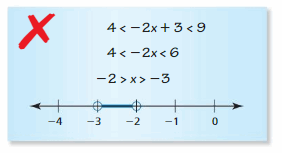
Answer:

Question 22.

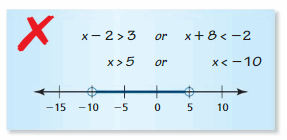
Answer:
The given inequality is:
x – 2 > 3 or x + 8 < -2
So,
x > 3 + 2 or x < -2 – 8
x > 5 or x < -10
Hence,
The representation of the solutions of the inequality in the graph is:

Question 23.
MODELING WITH MATHEMATICS
Write and solve a compound inequality that represents the possible temperatures (in degrees Fahrenheit) of the interior of the iceberg.

Answer:

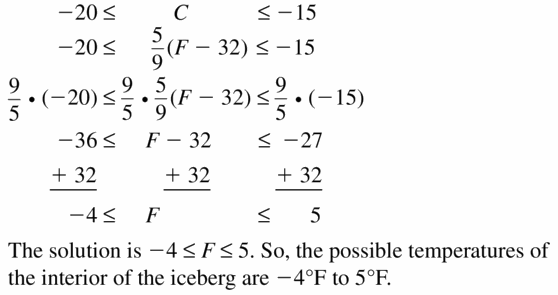
Question 24.
PROBLEM-SOLVING
A ski shop sells skis with lengths ranging from 150 centimeters to 220 centimeters. The shop says the length of the skis should be about 1.16 times a skier’s height (in centimeters). Write and solve a compound inequality that represents the heights of skiers the shop does not provide skis for.
Answer:
The compound inequality that represents the heights of skiers the shop does not provide skis for is:
129.3 centimeters > h > 189.7 centimeters

Explanation:
It is given that a ski shop sells skis with lengths ranging from 150 centimeters to 220 centimeters.
It is also given that the shop says the length of the skis should be about 1.16 times a skier’s height (in centimeters).
Now,
Let x be the possible length of the skis
Let h be the possible height of the skiers for whom the shop does not provide skis for
So,
The inequality that represents the lengths of the skis is:
x < 150 centimeters or x > 220 centimeters
So,
The compound inequality that represents the length of the skis is:
150 centimeters > x > 220 centimeters
But,
x = 1.16h
So,
150 centimeters > 1.16h > 220 centimeters
(150 / 1.16) centimeters > h > (220 / 1.16) centimeters
129.3 centimeters > h > 189.7 centimeters
Hence, from the above,
We can conclude that the compound inequality that represents the heights of skiers the shop does not provide skis for is:
129.3 centimeters > h > 189.7 centimeters

In Exercises 25–30, solve the inequality. Graph the solution, if possible.

Question 25.
22 < -3c + 4 < 14
Answer:

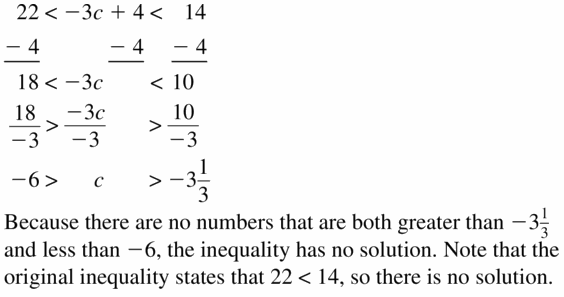
Question 26.
2m – 1 ≥ 5 or 5m > -25
Answer:
The given inequality is:
2m – 1≥ 5 or 5m > -25
So,
2m ≥ 5 + 1 or m > -25 / 5
2m ≥ 6 or m > -5
m ≥ 6 / 2 or m > -5
m ≥ 3 or m > -5
Hence, from the above
We can conclude that the solutions to the given inequality are:
m ≥ 3 or m > -5
The compound inequality of the solutions of the given inequality is:
m > -5
The representation of the solutions of the given inequality in the graph is:

Question 27.
-y + 3 ≤ 8 and y + 2 > 9
Answer:

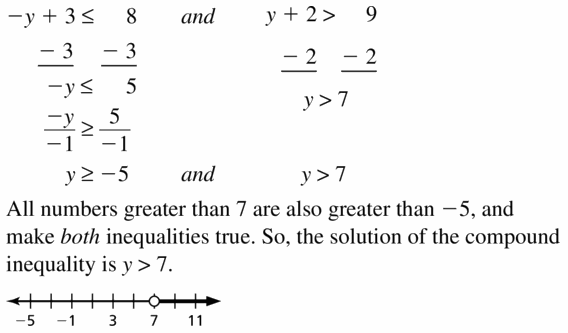
Question 28.
x – 8 ≤ 4 or 2x + 3 > 9
Answer:
The given inequality is:
x – 8 ≤ 4 or 2x + 3 > 9
So,
x ≤ 4 + 8 or 2x >  9 – 3
x ≤ 12 or 2x > 6
x ≤ 12 or x > 6 / 2
x ≤ 12 or x > 3
Hence, from the above,
We can conclude that the solutions to the given inequality are:
x ≤ 12 or x > 3
The compound inequality of the solutions of the given inequality is:
3 < x ≤ 12
The representation of the solutions of the inequalities in the graph is:

Question 29.
2n + 19 ≤ 10 + n or -3n + 3 < -2n + 33
Answer:

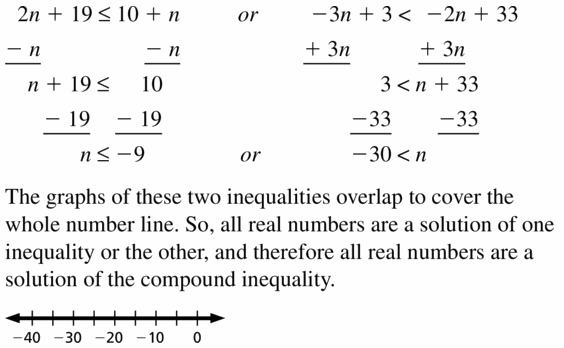
Question 30.
3x – 18 < 4x – 23 and x – 16 < -22
Answer:
The given inequality is:
3x – 18 < 4x – 23 and x – 16 < -22
So,
3x – 4x < -23 + 18 and x < -22 + 16
-x < -5 and x < – 6
x < 5 and x < -6
Hence, from the above,
We can conclude that the solutions to the given inequality are:
x < 5 and x < -6
The compound inequality that represents the solutions of the given inequality is:
x < 5
The representation of the solutions of the given inequality in the graph is:

Question 31.
REASONING
Fill in the compound inequality and 5(x + 2) ≥ 2(x + 8) with <, ≤, >, or ≥ so that the solution is only one value.
Answer:

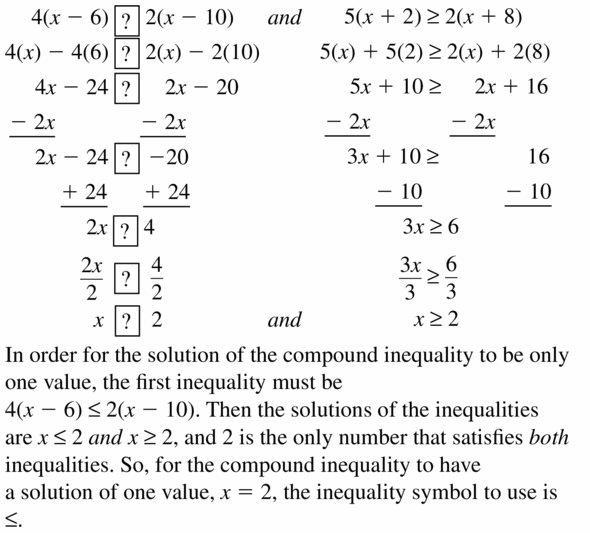
Question 32.
THOUGHT-PROVOKING
Write a real-life story that can be modeled by the graph.
Answer:
The real-life situation that can be modeled by the graph is:
Suppose we have 100 children in a school. Out of the 100 children, there are 60 boys and the rest are girls.
The attendance of all the boys in a particular month is 50% and all of the girls is 70%. Mark the percentage attendance that is between the attendance of all the boys and girls?
The graph representing the above real-life situation is:

Question 33.
MAKING AN ARGUMENT
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Use the triangle shown to write and solve three inequalities. Your friend claims the value of x can be 1. Is your friend correct? Explain.

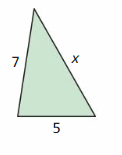
Answer:

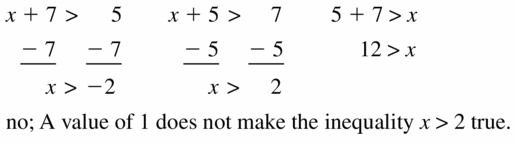
Question 34.
HOW DO YOU SEE IT?
The graph shows the annual profits of a company from 2006 to 2013.

a. Write a compound inequality that represents the annual profits from 2006 to 2013.
Answer:
The given graph is:

From the graph,
We can observe that the annual profits from 2006 to 2013
So,
The minimum value in the graph is: $65 million
The highest value in the graph is: $100 million
Let x be the annual profit
Hence,
The inequalities that represent the annual profits from 2006 to 2013 are:
x ≥ $65 million and x ≤ $100 million
So,
The compound inequality that represents the annual profits from 2006 to 2013 is:
$65 million ≤ x ≤ $100 million

b. You can use the formula P = R – C to find the profit P, where R is the revenue and C is the cost. From 2006 to 2013, the company’s annual cost was about $125 million. Is it possible the company had annual revenue of $160 million from 2006 to 2013? Explain.
Answer:
Yes, it is possible that the company had annual revenue of $160 million from 2006 to 2013

Explanation:
From part (a),
The total profit from 2006 to 2013 is:
P = 65 + 70 + 85 + 50 + 65 + 70 + 90
= $575 million
It is given that you can use the formula P = R – C to find the profit P, where R is the revenue and C is the cost.
It is also given that from 2006 to 2013, the company’s annual cost was about $125 million.
So,
P = R – C
R = P + C
R = 575 + 125
= $700 million
Hence, from the above,
We can conclude that it is possible that the company had annual revenue of $160 million from 2006 to 2013

Maintaining Mathematical Proficiency

Solve the equation. Graph the solutions, if possible.

Question 35.
| \(\frac{d}{9}\) | = 6
Answer:

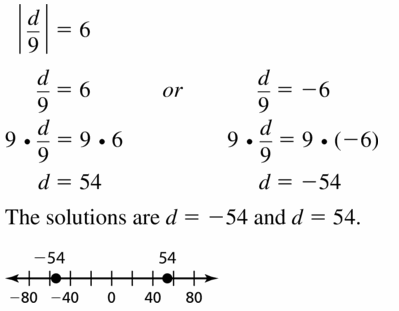
Question 36.
7 | 5p – 7 | = -21
Answer:
The given absolute value equation is:
7 | 5p – 7 | = 21
So,
| 5p – 7 | = -21 / 7
| 5p – 7 | = -3
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
5p – 7 = -3 or 5p – 7 = – (-3)
5p = -3 + 7 or 5p = 3 + 7
5p = 4 or 5p = 10
p = \(\frac{4}{5}\) or p = 2
p = 0.8 or p = 2
p = 1 [Approx. value] or p = 2
Hence, from the above,
We can conclude that the solutions to the given absolute value equation are:
p = 1 or p = 2
The representation of the solutions of the given absolute value equation in the graph is:

Question 37.
| r + 2 | = | 3r – 4 |
Answer:

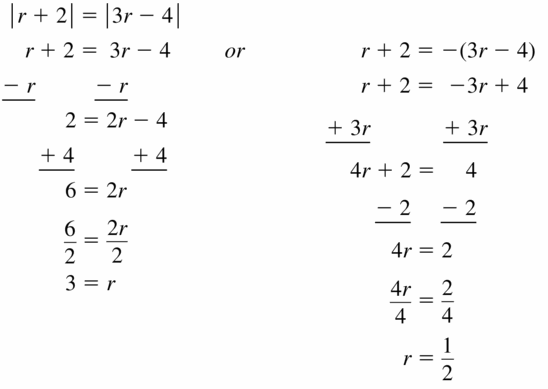
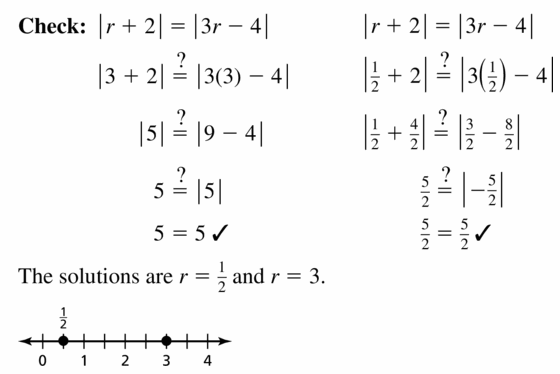
Question 38.

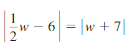
Answer:
The given absolute value equation is:
| \(\frac{1}{2}\)w – 6 | = | w + 7 |
So,
\(\frac{1}{2}\)w – 6 = w + 7
\(\frac{1}{2}\)w – w = 7 + 6
–\(\frac{1}{2}\)w = 13
w = 13 (-2)
w = -26
Hence, from the above,
We can conclude that the solution to the given absolute value equation is:
w = -26
The representation of the solution of the given absolute value equation in the graph is:

Find and interpret the mean absolute deviation of the data.

Question 39.
1, 1, 2, 5, 6, 8, 10, 12, 12, 13
Answer:

Question 40.
24, 26, 28, 28, 30, 30, 32, 32, 34, 36
Answer:
The given numbers are:
24, 26, 28, 28, 30, 30, 32, 32, 34, 36
We know that,
Mean = \(\frac{The sum of the given numbers}{The total number of numbers}\)
= \(\frac{24 + 26+ 28 + 28 + 30 + 30 + 32 + 32 + 34 + 36}{10}\)
= \(\frac{300}{10}\)
= 30
Now,
We know that,
Absolute deviation = ( The mean ) – ( Given number )
So,
Absolute deviations are:
30 – 24, 30 – 26, 30 – 28, 30 – 28, 30 – 30, 30 – 30, 30 – 32, 30 – 32, 30 – 34, 30 – 36
= 6, 4, 2, 2, 0, 0, -2, -2, -6, -4
So,
Absolute Mean deviation = \(\frac{Sum of Absolute deviations}{The numebr of absolute deviations}\)
= \(\frac{6 + 4 + 2 + 2 + 0 + 0 – 2 – 2 – 6 – 4}{10}\)
= \(\frac{0}{10}\)
= 0
Hence, from the above,
We can conclude that there is no deviation

Lesson 2.6 Solving Absolute Value Inequalities

Essential Question
How can you solve an absolute value inequality? Solving an Absolute Value Inequality Algebraically
EXPLORATION 1
Solving an Absolute Value Inequality Algebraically
Work with a partner.
Consider the absolute value inequality | x + 2 | ≤ 3.
a. Describe the values of x + 2 that make the inequality true. Use your description to write two linear inequalities that represent the solutions of the absolute value inequality.
b. Use the linear inequalities you wrote in part (a) to find the solutions of the absolute value inequality.

c. How can you use linear inequalities to solve an absolute value inequality?
Answer:
The given absolute value equation is:
| x + 2 | ≤ 3
a.
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x + 2 ≤ 3 or x + 2 ≤ -3
x ≤ 3 – 2 or x ≤ -3 – 2
x ≤ 1 or x ≤ -5
Hence, from the above,
We can conclude that the solutions to the given absolute value equation is:
x ≤ 1 or x ≤ -5

b.
The given absolute value equation is:
| x + 2 | ≤ 3
From part (a),
The solutions of the given absolute value equation are:
x ≤ 1 or x ≤ -5
We know that,
| x | = x for x > 0
| x | = -x for x < 0
Now,
For x = 1,
| 1 + 2 | ≤ 3
| 3 | ≤ 3
3 ≤ 3
For x = -5,
| -5 + 2 | ≤ 3
| -3 | ≤ 3
3 ≤ 3

c.
The following are the steps to solve the absolute value inequality:
A) Isolate the absolute value expression on the left side of the inequality
B) If the number on the other side of the inequality sign is negative, then your equation either has no solution or all real numbers as solutions
C) Remove the absolute value bars by setting up a compound inequality
D) Solve the inequalities

EXPLORATION 2
Solving an Absolute Value Inequality Graphically
Work with a partner. Consider the absolute value inequality
| x + 2 | ≤ 3.
a. On a real number line, locate the point for which | x + 2 | ≤ 3

Answer:
The given absolute value inequality is:
| x + 2 | ≤ 3
From Exploration 1,
The solutions of the absolute value inequality | x + 2 | ≤ 3 are:
x ≤ 1 and x ≤ -5
The compound inequality of the solution of the given absolute value inequality is:
x ≤ 1 ( Since the absolute value inequality can never be negative )
Now,
The given graph is:

Hence,
The representation of the solutions of the absolute value inequality is:

b. Locate the points that are within 3 units from the point you found in part (a). What do you notice about these points?
Answer:
From part (a),
The compound inequality that represents the solution of the given absolute value inequality is:
x ≤ 1
The points that are within 3 units from the point x ≤ 1, i.e., the given point + 3
So,
1 + 3 = 4
Hence,
The point we have to locate in the graph is:
x ≤ 4
Hence,
The representation of the compound inequality of the given absolute value inequality in the graph is:

c. How can you use a number line to solve an absolute value inequality?
Answer:
You begin the marking of the points on the number line by making it into separate equations and then solving them separately. An absolute value equation has no solution if the absolute value expression equals a negative number since an absolute value can never be negative. You can write an absolute value inequality as a compound value inequality

EXPLORATION 3
Solving an Absolute Value Inequality Numerically
Work with a partner.

Solving an Absolute Value Inequality Numerically
Work with a partner. Consider the absolute value inequality | x + 2 | ≤ 3.
a. Use a spreadsheet, as shown, to solve the absolute value inequality.
b. Compare the solutions you found using the spreadsheet with those you found in Explorations 1 and 2. What do you notice?
c. How can you use a spreadsheet to solve an absolute value inequality?
Answer:

Communicate Your Answer

Question 4.
How can you solve an absolute value inequality?
Answer:
Isolate the absolute value expression on the left side of the inequality. If the number on the other side of the inequality sign is negative, your equation either has no solution or all real numbers as solutions. Use the sign of each side of your inequality to decide which of these cases holds.

Question 5.
What do you like or dislike about the algebraic, graphical, and numerical methods for solving an absolute value inequality? Give reasons for your answers.
Answer:
We have to use algebraic, graphical, and numerical methods for solving an absolute value inequality depending on the situation
The algebraic and graphical methods for solving an absolute value inequality are useful when the size of the inequality is small i.e., have only 1 variable

2.6 Lesson

Monitoring Progress

Solve the inequality. Graph the solution, if possible

Question 1.
| x | ≤ 3.5
Answer:
The given absolute value inequality is:
| x | ≤ 3.5
We know that,
| x | =x for x > 0
| x | = -x for x < 0
So,
x ≤ 3.5
x ≤ 4 [Approximate value}
Hence, from the above,
We can conclude that the solution of the given absolute value inequality is:
x ≤ 4 [Approximate value]
The representation of the solution of the given absolute value inequality in the graph is:

Question 2.
| k – 3 | < -1
Answer:
The given absolute value inequality is:
| k – 3 | < -1
We know that,
If the number on the other side of the absolute value expression is negative, then the given absolute value equation has no solution or has real numbers as a solution
Hence, from the above,
We can conclude that the given absolute value inequality has no solution

Question 3.
| 2w – 1 | < 11
Answer:
The given absolute value inequality is:
| 2w – 1 | < 11
We know that,
| x | =x for x > 0
| x | = -x for x < 0
So,
2w – 1 < 11
2w < 11 + 1
2w < 12
w < 12 /  2
w < 6
Hence, from the above,
We can conclude that the solution of the given absolute value inequality is:
w < 6
The representation of the solution of the given absolute value inequality in the graph is:

Question 4.
| x + 3 | > 8
Answer:
The given absolute value inquality is:
| x + 3 | > 8
We know that,
| x | = xfor x > 0
| x | = -x for x < 0
So,
x + 3 > 8
x > 8 – 3
x > 5
Hence, from the above,
We can conclude that the solution of the given absolute value inequality is:
x > 5
The representation of the solution of the given absolute value inequality in the graph is:

Question 5.
| n + 2 | – 3 ≥ -6
Answer:
The given absolute value inequality is:
| n + 2 | – 3 ≥ -6
So,
| n + 2 | ≥ -6 + 3
| n + 2 | ≥ -3
We know that,
If the number on the other side of the absolute value expression is negative, then the given absolute value equation has no solution or has real numbers as a solution
Hence, from the above,
We can conclude that the given absolute value inequality has no solution

Question 6.
3 | d + 1 | – 7 ≥ -1
Answer:
The given absolute value inequality is:
3 | d + 1 | – 7 ≥ -1
So,
3 | d + 1 | ≥ -1 + 7
3 | d + 1 | ≥ 6
| d + 1 | ≥ 6 / 3
| d + 1 | ≥ 2
We know that,
| x | = x for x > 0
| x | = -x for x < 0
Hence,
d + 1 ≥ 2
d ≥ 2 – 1
d ≥ 1
Hence, from the above,
We can conclude that the solution of the given absolute value inequality is:
d ≥ 1
The representation of the solution of the given inequality in the graph is:

Question 7.
WHAT IF?
You are willing to pay the mean price with an absolute deviation of at most $75. How many of the computer prices meet your condition?
Answer:

Solving Absolute Value Inequalities 2.6 Exercises

Question 1.
REASONING
Can you determine the solution of | 4x – 2 | ≥ -6 without solving it? Explain
Answer:

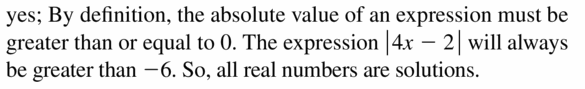
Question 2.
WRITING
Describe how solving | w – 9 | ≤ 2 is different from solving | w – 9 | ≥ 2.
Answer:
The given absolute value inequalities are:
| w – 9 | ≤ 2 and | w – 9 | ≥ 2
Now,
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
w – 9 ≤ 2 and w – 9 ≥ 2
w ≤ 2 + 9 and w ≥ 2 + 9
w ≤ 11 and w ≥ 11
w – 9 ≤ -2 and w – 9 ≥ -2
w ≤ -2 + 9 and w ≥ -2 + 9
w ≤ 7 and w ≥ 7
Hence, from the above,
We can conclude that the given absolute value inequalities are different by observing the above values for the 2 absolute value inequalities

Monitoring Progress and Modeling with Mathematics 

In Exercises 3–18, solve the inequality. Graph the solution, if possible.

Question 3.
| x | < 3
Answer:

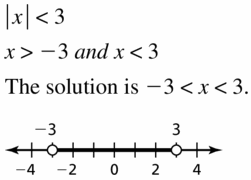
Question 4.
| y | ≥ 4.
Answer:
The given absolute value inequality is:
| y | ≥ 4
We know that,
| x | = x for x > 0
| x | = -x for x < 0
Hence,
The solutions for the given absolute value inequality is:
y ≥ 4 or y ≤ -4
The representation of the compound inequality solution of the given absolute value inequality is:

Question 5.
| d + 9 | > 3
Answer:

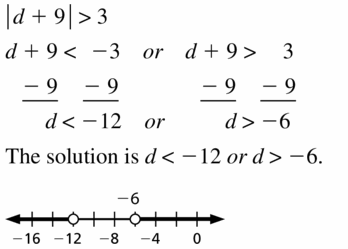
Question 6.
| h – 5 | ≤ 10
Answer:
The given absolute value inequality is:
| h – 5 | ≤ 10
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
h – 5 ≤ 10
h ≤ 10 + 5 and h ≥ -10 + 5
h ≤ 15 and h ≥ -5
Hence,
The compound inequality of the solutions of the given absolute value inequality are:
-5 ≤  h ≤  15
The representation of the compound inequality in the graph is:

Question 7.
| 2s – 7 | ≥ -1
Answer:

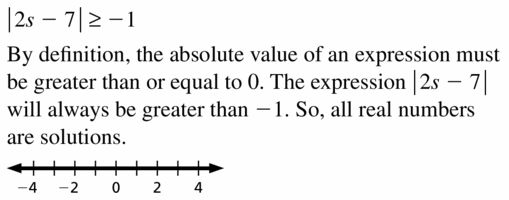
Question 8.
| 4c + 5 | > 7
Answer:
The given absolute value inequality is:
| 4c + 5 | > 7
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
4c + 5 > 7 or 4c + 5 < -7
4c > 7 – 5 or 4c < -7 – 5
4c > 2 or 4c < -12
c > \(\frac{2}{4}\) or c < –\(\frac{4}{12}\)
c > \(\frac{1}{2}\) or c < –\(\frac{1}{3}\)
Hence,
The solutions of the given absolute value equation are:
c > \(\frac{1}{2}\) or c < –\(\frac{1}{3}\)
c > 1 or c < 0 [ Approximate values of the inequality ]
The representation of the solutions of the given absolute value inequality in the graph is:

Question 9.
| 5p + 2 | < -4
Answer:

Question 10.
| 9 – 4n | < 5
Answer:
The given absolute value inequality is:
| 9 – 4n | < 5
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
9 – 4n < 5 and 9 – 4n > -5
9 – 5 < 4n and 9 + 5 > 4n
4 < 4n and 14 > 4n
4n > 4 and 4n < 14
n > 4/ 4 and n < 14 / 4
n > 1 and n < 7 / 2
n > 1 and n < 3.5
Hence,
The solutions of the given absolute value inequality are:
n > 1 and n < 3.5
The compound solution of the solutions of the given absolute value inequality is:
1 < n < 3.5
The representation of the compound inequality of the solutions of the given inequality in the graph is:

Question 11.
| 6t – 7 | – 8 ≥ 3
Answer:

Question 12.
| 3j – 1 | + 6 > 0
Answer:
The given absolute value inequality is:
| 3j – 1 | + 6 > 0
So,
| 3j – 1 | > 0 – 6
| 3j – 1 | > -6
We know that,
By definition of absolute values, the absolute value of an expression must be greater than or equal to 0
So,
The expression | 3j – 1 |  will always be greater than -6
Hence,
For the given absolute value inequality, all the real numbers are solutions

Question 13.
3 | 14 – m | > 18
Answer:

Question 14.
-4 | 6b – 8 | ≤ 12
Answer:
The given absolute value inequality is:
-4 | 6b – 8 | ≤ 12
So,
| 6b – 8 | ≤ -3
We know that,
By definition of absolute values, the absolute value of an expression must be greater than or equal to 0.
So,
The expression | 6b – 8 | must not be less than -3
Hence,
For the given absolute value inequality, there is no solution

Question 15.
2 | 3w + 8 | ≥ 13
Answer:

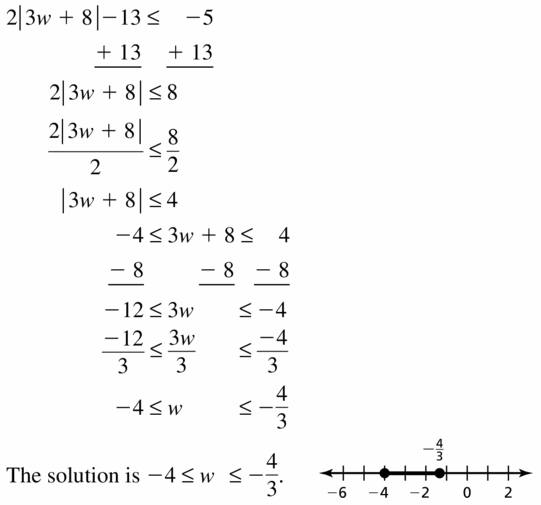
Question 16.
3 | 2 – 4u | + 5 < -13
Answer:
The given absolute value inequality is:
3 | 2 – 4u | + 5 < -13
So,
3 | 2 – 4u | < -13 – 5
3 | 2 – 4u | < -18
| 2 – 4u | < -6
We know that,
By definition of absolute values, the absolute value of an expression must be greater than or equal to 0.
So,
The expression | 2 – 4u | must not be less than -6
Hence,
For the given absolute value inequality, there is no solution

Question 17.
6 | -f + 3 | + 7 > 7
Answer:

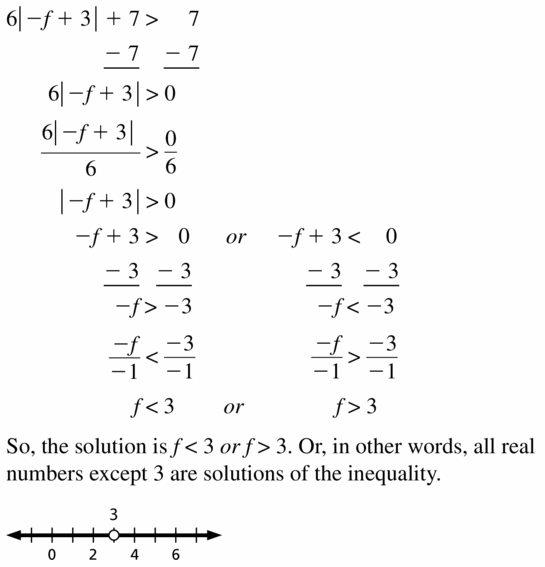
Question 18.
\(\frac{2}{3}\) |4v + 6 | – 2 ≤ 10
Answer:
The given absolute value inequality is:
\(\frac{2}{3}\) | 4v + 6 | – 2 ≤ 10
\(\frac{2}{3}\) | 4v + 6 | ≤ 10 + 2
\(\frac{2}{3}\) | 4v + 6 | ≤ 12
| 4v + 6 | ≤ 12 × \(\frac{3}{2}\)
| 4v + 6 | ≤ 18
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
4v + 6 ≤ 18 and 4v + 6 ≥ -18
4v ≤ 18 – 6 and 4v ≥ -18 – 6
4v ≤ 12 and 4v ≥ -24
v ≤ 12 / 4 and v ≥ -24 / 4
v ≤ 3 and v ≥ -6
Hence, from the above,
We can conclude that the solutions of the given absolute value inequality are:
v ≤ 3 and v ≥ -6
The representation of the compound inequality of the solutions of the given absolute value inequality is:
-6 ≤ v ≤ 3
The representation of the compound inequality in the graph is:

Question 19.
MODELING WITH MATHEMATICS
The rules for an essay contest say that entries can have 500 words with an absolute deviation of at most 30 words. Write and solve an absolute value inequality that represents the acceptable numbers of words.
Answer:

Question 20.
MODELING WITH MATHEMATICS
The normal body temperature of a camel is 37°C. This temperature varies by up to 3°C throughout the day. Write and solve an absolute value inequality that represents the range of normal body temperatures (in degrees Celsius) of a camel throughout the day.

Answer:
The absolute value inequality that represents the range of normal body temperatures of a camel throughout the day is:
34°C ≤ t ≤ 40°C

Explanation:
It is given that the normal body temperature of a camel is 37°C and this temperature varies by up to 3°C throughout the day.
Let t be the temperature in °C
So,
The absolute value inequality that represents the range of normal body temperatures of a camel throughout the day is:
37 – 3 ≤ t ≤ 37 + 3
34°C ≤ t ≤ 40°C

ERROR ANALYSIS
In Exercises 21 and 22, describe and correct the error in solving the absolute value inequality.

Question 21.

Answer:

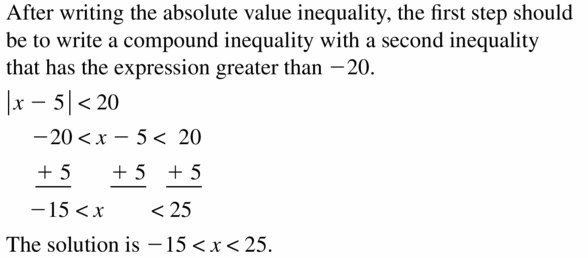
Question 22.

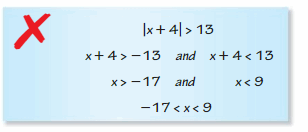
Answer:
The given absolute value inequality is:
| x + 4 | > 13
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x + 4 > 13 or x + 4 < -13
x > 13 – 4 or x < -13 – 4
x > 9 or x < -17
Hence, from the above,
We can conclude that the solutions of the given absolute value inequality are:
x > 9 or x < -17

In Exercises 23–26, write the sentence as an absolute value inequality. Then solve the inequality.

Question 23.
A number is less than 6 units from 0.
Answer:

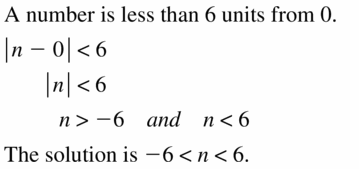
Question 24.
A number is more than 9 units from 3.
Answer:
The given worded form is:
A number is more than 9 units from 3
Let n be the number
Hence,
The representation of the given worded form in the form of absolute value inequality is:
| n – 3 | > 9
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
n – 3 > 9 or n – 3 < -9
n > 9 + 3 or n < -9 + 3
n > 12 or n < -6
Hence, from the above,
We can conclude that the solutions o the given absolute value inequality is:
n > 12 or n < -6

Question 25.
Half of a number is at most 5 units from 14.
Answer:

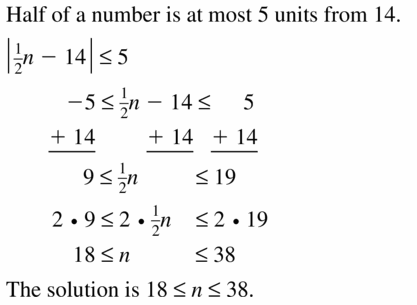
Question 26.
Twice a number is no less than 10 units from -1.
Answer:
The given worded form is:
Twice a number is no less than 10 units from -1
Let x be the number
So,
The representation of the given worded form in the form of absolute value inequality is:
| 2x – (-1) | > 10
So,
| 2x + 1 | > 10
We know that,
| x | = x for x > 0
| x | = -x for x < 0
Hence,
2x + 1 > 10 or 2x + 1 < -10
2x > 10 – 1 or 2x < -10 – 1
2x > 9 or 2x < -11
x > \(\frac{9}{2}\) or x < –\(\frac{11}{2}\)
Hence, from the above,
We can conclude that the solutions of the given absolute value inequality is:
x > \(\frac{9}{2}\) or x < –\(\frac{11}{2}\)

Question 27.
PROBLEM SOLVING
An auto parts manufacturer throws out gaskets with weights that are not within 0.06 pound of the mean weight of the batch. The weights (in pounds) of the gaskets in a batch are 0.58, 0.63, 0.65, 0.53, and 0.61. Which gasket(s) should be thrown out?
Answer:

Question 28.
PROBLEM-SOLVING
Six students measure the acceleration (in meters per second ) of an object in free fall. The measured values are shown. The students want to state that the absolute deviation of each measured value x from the mean is at most d. Find the value of d.
10.56, 9.52, 9.73, 9.80, 9.78, 10.91
Answer:
The value of d is: 0.86

Explanation:
The given numbers are:
10.56, 9.52, 9.73, 9.80, 9.78, 10.91
We know that,
Mean = \(\frac{Sum of the given observations}{Number of observations}\)
= \(\frac{10.56 + 9.52 + 9.73 + 9.80 + 9.78 + 10.91}{6}\)
= \(\frac{60.3}{6}\)
= 10.05
Now,
We know that,
Absolute deviation = Mean – ( Given observation)
It is given that that the measured value is x
Hence,
The representation of the absolute deviation in the form of absolute value inequality is:
| x – 10.05 | ≤ d
So,
| 10.56 – 10.05 | ≤ d
| 9.52 – 10.05 | ≤ d
| 9.73 – 10.05 | ≤ d
| 9.80 – 10.05 | ≤ d
| 9.78 – 10.05 | ≤ d
| 10.91 – 10.05 | ≤ d
So,
d ≥ 0.51
d ≥ 0.53
d ≥ 0.32
d ≥ 0.25
d ≥ 0.27
d ≥ 0.86
Hence, from the above,
We can conclude that the value of d will be the highest deviation from the mean value
The value of d is: 0.86

MATHEMATICAL CONNECTIONS
In Exercises 29 and 30, write an absolute value inequality that represents the situation. Then solve the inequality.

Question 29.
The difference between the areas of the figures is less than 2.

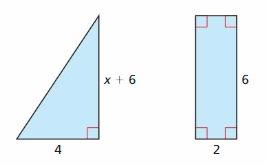
Answer:

Question 30.
The difference between the perimeters of the figures is less than or equal to 3.

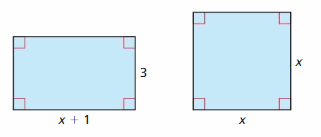
Answer:
The given figures are:

From the above,
The given figures are: Rectangle and square
We know that,
The perimeter of a rectangle = 2 ( Length + Width )
The perimeter of a square = 4 ( Side )
So,
The perimeter of a rectangle = 2 ( 3 + x + 1 ) = 2 ( x + 4 )
The perimeter of a square = 4 (x) = 4x
It is given that the difference of the perimeters of the given figures is less than or equal to 3
So,
| 2 ( x + 4 ) – 4x | ≤ 3
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
2 (x + 4) – 4x ≤3 and 2 ( x + 4 ) – 4x ≥ -3
2x + 8 – 4x ≤ 3 and 2x + 8 – 4x ≥ -3
8 – 2x ≤ 3 and 8- 2x ≥ -3
-2x ≤ 3 – 8 and -2x ≥ -3 – 8
-2x ≤ -5 and -2x ≥ -11
2x ≤ 5 and 2x ≥ 11
x ≤ \(\frac{5}{2}\) and x ≥ \(\frac{11}{2}\)
Hence, from the above,
We can conclude that the compound inequality for the solutions of the given absolute value inequality is:
\(\frac{11}{2}\) ≤ x ≤ \(\frac{5}{2}\)

REASONING
In Exercises 31–34, tell whether the statement is true or false. If it is false, explain why.

question 31.
If a is a solution of | x + 3 | ≤ 8, then a is also a solution of x + 3 ≥ -8.
Answer:

Question 32.
If a is a solution of | x + 3 | > 8, then a is also a solution of x + 3 > 8.
Answer:
The given statement is true

Explanation:
The given statement is:
If a is a solution of | x + 3 | > 8, then a is also a solution of x + 3 > 8
Now,
The given inequality is:
| x + 3 | > 8
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x + 3 > 8 or x + 3 < -8
We know that,
The value of the absolute value expression must be greater than or equal to 0
So,
x + 3 < -8 has no solution
So,
a is a solution of x + 3 > 8
Hence, from the above,
We can conclude that the given statement is true

Question 33.
If a is a solution of | x + 3 | ≥ 8, then a is also a solution of x + 3 ≥ -8.
Answer:

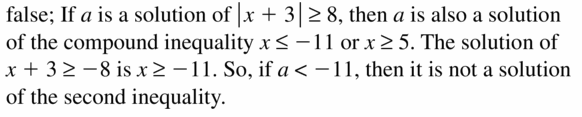
Question 34.
If a is a solution of x + 3 ≤  -8, then a is also a solution of | x + 3 | ≥ 8.
Answer:
The given statement is true

Explanation:
The given statement is:
If a is a solution of x + 3 ≤ -8, then a is a solution of | x + 3 | ≥ 8
Now,
The given absolute value inequality is:
| x + 3 | ≥ 8
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x + 3 ≥ 8 or x + 3 ≤ -8
If a is a solution of x + 3  ≥ 8, then a is also a solution of x + 3 ≤ -8
Hence, from the above,
We can conclude that the given statement is true

Question 35.
MAKING AN ARGUMENT
One of your classmates claims that the solution of | n | > 0 is all real numbers. Is your classmate correct? Explain your reasoning.
Answer:

Question 36.
THOUGHT-PROVOKING
Draw and label a geometric figure so that the perimeter P of the figure is a solution to the inequality | P – 60 | ≤ 12.
Answer:
The given absolute value inequality is:
| p – 60 | ≤ 12
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
p – 60 ≤ 12 and p – 60 ≥ -12
p ≤ 12 + 60 and p ≥ -12 + 60
p ≤ 72 and p ≥ 48
Hence,
The representation of the compound inequality of the perimeter of the figure is:
48 ≤ p ≤ 72
Now, find the value of 4p i.e., the perimeter of the square
So,
192 ≤ 4p ≤ 288
Hence, from the above,
We can conclude that the perimeter is represented for the perimeter of the square

Question 37.
REASONING
What is the solution of the inequality | ax + b | < c, where c < 0? What is the solution of the inequality | ax + b | > c, where c < 0? Explain.
Answer:

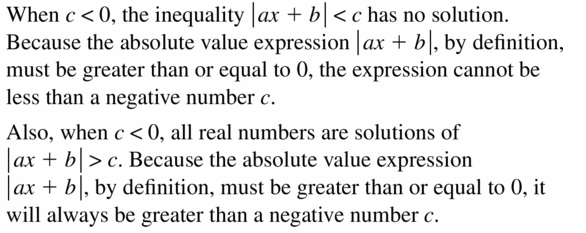
Question 38.
HOW DO YOU SEE IT?
Write an absolute value inequality for each graph.

How did you decide which inequality symbol to use for each inequality?
Answer:
The given graphs are:

a.
From the given graph,
The 1st marked line starts from -1 including -1 and continued till the left end of the number line
The 2nd marked line starts from 5 including from 5 and continued till the right end of the number line
Hence,
The representation of the marked lines in the form of absolute value inequality is:
| x + 1 | ≤ 3 and | x – 5 | ≥ 1

b.
From the given graph,
The marked line starts from -1 excluding -1 and continued till 5 on the right end of the number line
Hence,
The representation of the marked line in the form of absolute value inequality is:
| x + 1 | > 6
c.
From the given graph,
The marked line starts from -1 including -1 and continued till 5 on the right end of the number line
Hence,
The representation of the marked line in the form of absolute value inequality is:
| x + 1 | ≥ 6
d.
Fro the given graph,
The 1st marked line starts from -1 excluding -1 and continued till the left end of the number line
The 2nd marked line starts from 5 excluding 5 and continued till the right end of the number line
Hence,
The representation of the marked lines in the form of absolute value inequality is:
| x + 1 | < 3 and | x – 5 | > 1
If the marked point is indicated on the number line and if that marked line continued till the right end of the number line, then we will use ≥
If the marked point is not indicated on the number line and if that marked line continued till the right end of the number line, then we will use >
If the marked point is indicated on the number line and if that marked line continued till the left end of the number line, then we will use ≤
If the marked point is not indicated on the number line and if that marked line continued till the left end of the number line, then we will use <

Question 39.
WRITING
Explain why the solution set of the inequality | x | < 5 is the intersection of two sets, while the solution set of the inequality | x | > 5 is the union of two sets.
Answer:

Question 40.
PROBLEM-SOLVING
Solve the compound inequality below. Describe your steps.
| x – 3 | < 4 and | x + 2 | > 8
Answer:
The given inequalities are:
| x + 3 | < 4 and | x + 2  | > 8
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x + 3 < 4 or x + 3 > -4 and x + 2 > 8 or x + 2 < -8
x < 4 – 3 or x > -4 – 3 and x > 8 – 2 or x < -8 – 2
x < 1 or x > -7 and x > 6 or x < -10
Hence,
The compound inequality of the solutions of the given absolute value inequalities are:
-7 < x < 1 and -10 > x > 6

Maintaining Mathematical Proficiency

Plot the ordered pair in a coordinate plane. Describe the location of the point.

Question 41.
A(1, 3)
Answer:

Question 42.
B(0, -3)
Answer:
In the graph,
X-axis:
The right side of the x-axis will be: +ve
The left side of the x-axis will be: -ve
Y-axis:
The top side of the y-axis will be: +ve
The downside of the y-axis will be: -ve
We know that,
The graph is divided into 4 quadrants. They are:
1st Quadrant: x: +ve and y: -ve
2nd Quadrant: x: -ve and y: +ve
3rd Quadrant: x: -ve and y: -ve
4th Quadrant: x: +ve and y: -ve
Hence,
B(0, -3) will be in the 4th Quadrant
The representation of point B in the graph is:

Question 43.
C(-4, -2)
Answer:

Question 44.
D(-1, 2)
Answer:
In the graph,
X-axis:
The right side of the x-axis will be: +ve
The left side of the x-axis will be: -ve
Y-axis:
The top side of the y-axis will be: +ve
The downside of the y-axis will be: -ve
We know that,
The graph is divided into 4 quadrants. They are:
1st Quadrant: x: +ve and y: -ve
2nd Quadrant: x: -ve and y: +ve
3rd Quadrant: x: -ve and y: -ve
4th Quadrant: x: +ve and y: -ve
Hence,
D(-1, 2) will be in the 2nd Quadrant
The representation of point D in the graph is:

Copy and complete the table.

Question 45.

Answer:

Question 46.

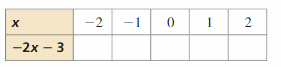
Answer:
The completed table is:

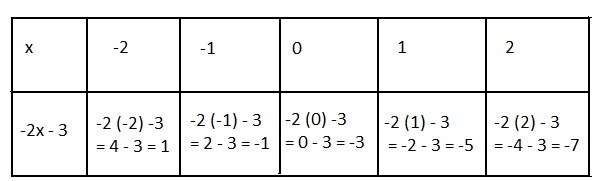
Solving Linear Inequalities Performance Task: Grading Calculations

2.5–2.6 What Did You Learn?

Core Vocabulary
compound inequality, p. 82
absolute value inequality, p. 88
absolute deviation, p. 90

Core Concepts
Section 2.5
Writing and Graphing Compound Inequalities, p. 82
Solving Compound Inequalities, p. 83

Section 2.6
Solving Absolute Value Inequalities, p. 88

Mathematical Practices

Question 1.
How can you use a diagram to help you solve Exercise 12 on page 85?
Answer:
In Exercise 12 on page 85,
The given diagram represents the maximum elevation of Mount Rainier
In the diagram,
The given maximum elevation of Mount Rainier is: 14,410 ft
So,
This 14,410 ft is divided into different types of elevation in Exercise 12

Question 2.
In Exercises 13 and 14 on page 85, how can you use structure to break down the compound inequality into two inequalities?
Answer:
In Exercises 13 and 14 on page 85,
First, perform the necessary mathematical operations so that only the variable must be present
So,
After performing the necessary mathematical operations, the structure of the compound inequality will be like
a < x < b or a > x > b
The breakdown of the compound inequality a < x < b will be like x >a and x < b
The breakdown of the compound inequality a > x > b will be like x < a and x > b
We can put the different types of inequality symbols in the breakdown of inequalities

Question 3.
Describe the given information and the overall goal of Exercise 27 on page 91.
Answer:
The given information is:
An auto parts manufacturer throws out gaskets with weights that are not within 0.06 pounds of the mean weight of the batch. The weights (in pounds) of the gaskets in a batch are 0.58, 0.63, 0.65, 0.53, and 0.61
The overall goal of Exercise 27:
Find the mean of the given weights and find the absolute deviation of the gaskets
The absolute deviation of the gaskets that are less than 0.0 pounds of the man weight should be thrown out

Question 4.
For false statements in Exercises 31–34 on page 92, use examples to show the statements are false.
Answer:
In Exercises 31 – 34 on page 92,
Exercises 33 and 34 are false
The Exercise 33 is: | x + 3 | ≥ 8
The Exercise 34 is: | x + 3 | ≥ 8
So,
In Exercise 33,
a is a solution for x + 3 ≥ 8 and x + 3 ≤ -8
In Exercise 34,
a is a solution of x + 3 ≥ 8 and x + 3 ≤ -8

Performance Task

Grading Calculations

You are not doing as well as you had hoped in one of your classes. So, you want to figure out the minimum grade you need on the final exam to receive the semester grade that you want. Is it still possible to get an A? How would you explain your calculations to a classmate?
To explore the answers to this question and more, go to

Solving Linear Inequalities Chapter Review

2.1 Writing and Graphing Inequalities (pp. 53–60)
a. A number x plus 36 is no more than 40. Write this sentence as an inequality.

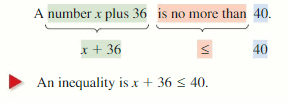
b. Graph w > −3.

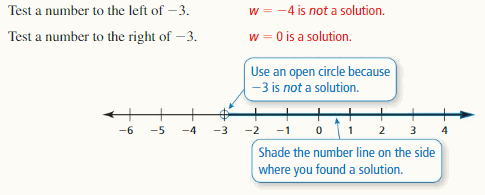
Write the sentence as an inequality.

Question 1.
A number d minus 2 is less than -1.
Answer:
The given worded form is:
A number d minus 2 is less than -1
Hence,
The representation of the given worded form in the form of inequality is:
d – 2 < -1

Question 2.
Ten is at least the product of a number h and 5.
Answer:
The given worded form is:
Ten is at least the product of a number h and 5
Hence,
The representation of the given worded form in the form of inequality is:
10 ≥ h(5)
10 ≥ 5h
10 / 5 ≥ h
2 ≥ h
h ≤ 2
Hence, from the above,
We can conclude that the representation of the given worded form in the form of inequality is:
h ≤ 2

Graph the inequality.

Question 3.
x > 4
Answer:
The given inequality is:
x > 4
Hence,
The representation of the given inequality in the graph is:

Question 4.
y ≤ 2
Answer:
The given inequality is:
y ≤ 2
Hence,
The representation of the given inequality in the graph is:

Question 5.
-1 ≥ z
Answer:
The given inequality is:
-1 ≥ z
z ≤ -1
Hence,
The representation of the given inequality in the graph is:

2.2 Solving Inequalities Using Addition or Subtraction (pp. 61–66)

Solve x + 2.5 ≤ −6. Graph the solution.

Solve the inequality. Graph the solution.

Question 6.
p + 4 < 10
Answer:
The given inequality is:
p + 4 < 10
So,
p < 10 – 4
p < 6
Hence, from the above,
We can conclude that the solution to the given inequality is p < 6
The representation of the solution of the given inequality in the graph is:

Question 7.
r – 4 < -6
Answer:
The given inequality is:
r – 4 < -6
So,
r < -6 + 4
r < -2
Hence, from the above,
We can conclude that the solution to the given inequality is r < -2
The representation of the solution of the given inequality in the graph is:

Question 8.
2.1 ≥ m – 6.7
Answer:
The given inequality is:
2.1 ≥ m – 6.7
So,
2.1 + 6.7 ≥ m
8.8 ≥ m
9 ≥ m [Approximate value]
m ≤ 9
Hence, from the above,
We can conclude that the solution to the given inequality is m ≤ 9
The representation of the solution of the given inequality in the graph is:

2.3 Solving Inequalities. Using Multiplication or Division

Solve \(\frac{n}{-10}\) > 5. Graph the solution.

Solve the inequality. Graph the solution.

Question 9.
3x > -21
Answer:
The given inequality is:
3x > -21
So,
x > -21 / 3
x > -7
Hence, from the above,
We can conclude that the solution to the given inequality is x > -7
The representation of the solution of the given inequality in the graph is:

Question 10.
-4 ≤ \(\frac{g}{5}\)
Answer:
The given inequality is:
-4 ≤ \(\frac{g}{5}\)
-4 (5) ≤ g
-20 ≤ g
g ≥ -20
Hence, from the above,
We can conclude that the solution to the given inequality is g ≥ -20
The representation of the solution of the given inequality in the graph is:

Question 11.
–\(\frac{3}{4}\)n ≤ 3
Answer:
The given inequality is:
–\(\frac{3}{4}\)n ≤ 3
n ≤ 3 × –\(\frac{4}{3}\)
n ≤ —\(\frac{3 × 4}{3}\)
n ≤ -4
Hence, from the above,
We can conclude that the solution to the given inequality is n ≤ -4
The representation of the solution of the given inequality in the graph is:

Question 12.
\(\frac{s}{-8}\) ≥ 11
Answer:
The given inequality is:
\(\frac{s}{-8}\) ≥ 11
s ≥ 11 (-8)
s ≥ -88
Hence, from the above,
We can conclude that the solution to the given inequality is s ≥ -88
The representation of the solution of the given inequality in the graph is:

Question 13.
36 < 2q
Answer:
The given inequality is:
36 < 2q
So,
36 / 2 < q
18 < q
q > 18
Hence, from the above,
We can conclude that the solution to the given inequality is q > 18
The representation of the solution of the given inequality in the graph is:

Question 14.
-1.2k > 6
Answer:
The given inequality is:
-1.2k > 6
So,
k > 6 / -1.2
k > -60 / 12
k > -5
Hence, from the above,
We can conclude that the solution to the given inequality is k > -5
The representation of the solution of the given inequality in the graph is:

2.4 Solving Multi-step Inequalities

Solve 22 + 3y ≥ 4. Graph the solution.

Solve the inequality. Graph the solution, if possible.

Question 15.
3x – 4 > 11
Answer:
The given inequality is:
3x – 4 > 11
So,
3x > 11 + 4
3x > 15
x > 15 / 3
x > 5
Hence, from the above,
We can conclude that the solution to the given inequality is x > 5
The representation of the solution of the given inequality in the graph is:

Question 16.
-4 < \(\frac{b}{2}\) + 9
Answer:
The given inequality is:
-4 < \(\frac{b}{2}\) + 9
-4 – 9 < \(\frac{b}{2}\)
-13 < \(\frac{b}{2}\)
-13 (2) < b
-26 < b
b > -26
Hence, from the above,
We can conclude that the solution of the given inequality is b > -26
The representation of the solution of the given inequality in the graph is:

Question 17.
7 – 3n ≤ n + 3
Answer:
The given inequality is:
7 – 3n ≤ n + 3
-3n – n ≤ 3 – 7
-4n ≤ -4
4n ≤ 4
n ≤ 4 / 4
n ≤ 1
Hence, from the above,
We can conclude that the solution to the given inequality is n ≤ 1
The representation of the solution of the given inequality in the graph is:

Question 18.
2(-4s + 2) ≥ -5s – 10
Answer:
The given inequality is:
2 (-4s +2) ≥ -5s – 10
So,
2 (-4s) + 2 (2) ≥ -5s – 10
-8s + 4 ≥ -5s – 10
-8s + 5s ≥ -10 –  4
-3s ≥ -14
3s ≥ 14
s ≥ 14 / 3
s ≥ 5 [ Approximate value }
Hence, from the above,
We can conclude that the solution of the given inequality is s ≥ 5
The representation of the solution of the given inequality in the graph is:

Question 19.
6(2t + 9) ≤ 12t – 1
Answer:
The given inequality is:
6(2t + 9) ≤ 12t – 1
So,
6 (2t) + 6 (9) ≤ 12t – 1
12t + 54 ≤ 12t – 1
1t – 12t + 54 ≤ -1
54 ≤ -1
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 20.
3r – 8 > 3(r – 6)
Answer:
The given inequality is:
3r – 8 > 3 ( r – 6 )
So,
3r – 8 > 3 (r) – 3 (6)
3r – 8 > 3r – 18
3r – 8 – 3r > -18
-8 > -18
8 > 18
Hence, from the above,
We can conclude that there is no solution to the given inequality

2.5 Solving Compound Inequalities

Solve −1 ≤ −2d + 7 ≤ 9. Graph the solution.

Question 21.
A number x is more than -6 and at most 8. Write this sentence as an inequality. Graph the inequality.
Answer:
The given worded form is:
A number x is more than -6 and at most 8
The representation of the given worded form in the form of inequality is:
x > -6 and x ≤ 8
Hence,
The representation of the solutions of the given worded form in the form of compound inequality is:
-6 < x ≤ 8
The representation of the compound inequality in the graph is:

Solve the inequality. Graph the solution.

Question 22.
19 ≥ 3z + 1 ≥ -5
Answer:
The given inequality is:
19 ≥ 3z + 1 ≥ -5
Subtract with -1 on both sides
So,
19 – 1 ≥ 3z + 1 – 1 ≥ -5 – 1
18 ≥ 3z ≥ -6
Divide by 3 on both sides
So,
(18 / 3) ≥ (3z / 3) ≥ (-6 / 3)
6 ≥ z ≥ -2
-2 ≤ z ≤ 6
Hence, from the above,
We can conclude that the compound inequality solution to the given inequality is:
-2 ≤ z ≤ 6
The representation of the compound inequality in the graph is:

Question 23.
\(\frac{r}{4}\) < -5 or -2r – 7 ≤ 3

Answer:
The given inequality is:
\(\frac{r}{4}\) < -5 or -2r – 7 ≤ 3
r < -5 (4) or -2r ≤ 3 + 7
r < -20 or -2r ≤ 10
r < -20 or r ≤ -5
Hence, from the above,
We can conclude that the solutions to the given inequality are:
r < -20 or r ≤ -5
The representations of the solutions of the given inequality in the graph is:

2.6 Solving Absolute Value Inequalities

Solve the inequality. Graph the solution, if possible.

Question 24.
| m | ≥ 10
Answer:
The given absolute value inequality is:
| m | ≥ 10
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
m ≥ 10 or m ≤ -10
We know that,
The value of absolute value expression must be greater than or equal to 0
So,
m ≥ 10
Hence, from the above,
We can conclude that the solution of the given absolute value inequality is m ≥ 10
The representation of the solution of the given absolute value inequality in the graph is:

Question 25.
| k – 9 | < -4
Answer:
The given absolute value inequality is:
| k – 9 | < 4
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
k – 9 < 4 and k – 9 > -4
k < 4 + 9 and k > -4 + 9
k < 13 and k > 5
Hence, from the above,
We can conclude that the solutions of the given absolute value inequality are:
k < 13 and k > 5
The representation of the compound inequality of the solutions of the given absolute inequality is:
5 < k < 13
The representation of the compound inequality in the graph is:

Question 26.
4 | f – 6 | ≤ 12
Answer:
The given absolute value inequality is:
4 | f – 6 | ≤ 12
| f – 6 | ≤ 3
We know that,
| x | = x for x > 0
| X | = -x for x < 0
So,
f – 6 ≤ 3 and f – 6 ≥ -3
f ≤ 3 + 6 and f ≥ -3 + 6
f ≤ 9 and f ≥ 3
Hence, from the above,
We can conclude that the solutions of the given absolute value inequality are:
f ≤ 9 and f ≥ 3
The representation of the compound inequality of the solutions of the given absolute value inequality is:
3 ≤ f ≤ 9
The representation of the compound inequality in the graph is:

Question 27.
5 | b + 8 | – 7 > 13
Answer:
The given absolute value inequality is:
5 | b + 8 | – 7 > 13
5 | b + 8 | > 13 + 7
5 | b + 8 | > 20
| b + 8 | > 4
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
b + 8  > 4 or b + 8 < -4
b > 4 + 8 or b < -4 – 8
b > 12 or b < -12
We know that,
The value of absolute value expression must be greater than or equal to 0
So,
b > 12
Hence, from the above,
We can conclude that the solution to the given absolute value inequality is b > 12
The representation of the solution of the given absolute value inequality in the graph is:

Question 28.
| -3g – 2 | + 1 < 6
Answer:
The given absolute value inequality is:
| -3g – 2 | + 1 < 6
– | 3g + 2 | < 6 – 1
– | 3g + 2 | < 5
| 3g + 2 | < -5
We know that,
The value of absolute value expression must be greater than or equal to 0
Hence, from the above,
We can conclude that there is no solution to the given absolute value inequality

Question 29.
| 9 – 2j | + 10 ≥ 2
Answer:
The given absolute value inequality is:
| 9 – 2j | + 10 ≥  2
| 9 – 2j | ≥ 2 – 10
| 9 – 2j | ≥  -8
We know that,
The value of absolute value expression must be greater than or equal to 0
Hence, from the above,
We can conclude that there is no solution to the given absolute value inequality

Question 30.
A safety regulation states that the height of a guardrail should be 106 centimeters with an absolute deviation of no more than 7 centimeters. Write and solve an absolute value inequality that represents the acceptable heights of a guardrail.
Answer:
The absolute value inequality that represents the acceptable heights of a guardrail is:
| x – 106 | ≤ 7 centimeters

Explanation:
It is given that a safety regulation states that the height of a guardrail should be 106 centimeters with an absolute deviation of no more than 7 centimeters.
Now,
We know that,
Absolute deviation = ( Mean ) – ( The given observation )
Let the Mean be x
So,
Absolute deviation = x – 106
Hence,
The absolute value inequality that represents the acceptable heights of a guardrail is:
| x – 106 | ≤ 7
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
x – 106 ≤ 7 and x – 106 ≥ -7
x ≤ 7 + 106 and x ≥ -7 + 106
x ≤ 113 and x ≥ 99
Hence, from the above,
We can conclude that the absolute value inequality that represents the acceptable heights of a guardrail is:
| x – 106 | ≤ 7

Solving Linear Inequalities Chapter Test

Write the sentence as an inequality.

Question 1.
The sum of a number y and 9 is at least -1.
Answer:
The given worded form is:
The sum of a number y and 9 is at least -1
Hence,
The representation of the given worded form in the form of inequality is:
y + 9 ≥ -1

Question 2.
A number r is more than 0 or less than or equal to -8.
Answer:
The given worded form is:
A number r is more than 0 or less than or equal to -8
Hence,
The representation of the given worded form in the form of inequality is:
r > 0 or r ≤ -8

Question 3.
A number k is less than 3 units from 10.
Answer:
The given worded form is:
A number k is less than 3 units from 10
Hence,
The representation of the given worded form in the form of inequality is:
k – 10 < 3

Solve the inequality. Graph the solution, if possible.

Question 4.
\(\frac{x}{2}\) – 5 ≥ -9
Answer:
The given inequality is:
\(\frac{x}{2}\) – 5 ≥ -9
\(\frac{x}{2}\) ≥ -9 + 5
\(\frac{x}{2}\) ≥ -4
x ≥ -4 (2)
x ≥ -8
Hence, from the above,
We can conclude that the solution to the given inequality is x ≥ -8
The representation of the solution of the given inequality in the graph is:

Question 5.
-4s < 6s + 1
Answer:
The given inequality is:
-4s < 6s + 1
So,
-4s – 6s < 1
-10s < 1
10s < -1
s < –\(\frac{1}{10}\)
s < -0.1
Hence, from the above,
We can conclude that the solution to the given inequality is s < -0.1
The representation of the solution of the given inequality in the graph is:

Question 6.
4p + 3 ≥ 2(2p + 1)
Answer:
The given inequality is:
4p + 3 ≥ 2 (2p + 1)
So,
4p + 3 ≥ 2 (2p) + 2 (1)
4p + 3 ≥ 4p + 2
4p – 4p + 3 ≥ 2
3 ≥ 2
Hence, from the above,
We can conclude that there is no solution for the given inequality

Question 7.
-7 < 2c – 1 < 10
Answer:
The given inequality is:
-7 < 2c – 1 < 10
Add 1 on both sides
So,
-7 + 1 < 2c – 1 + 1 < 10 + 1
-6 < 2c < 11
Divide by 3 on both sides
(-6 / 2) < (2c / 2) < (11 / 2)
-3 < c < 5.5
-3 < c < 6 [Approximate inequality]
Hence, from the above,
We can conclude that the solution to the given inequality is -3 < c < 6
The representation of the solution of the given inequality in the graph is:

Question 8.
-2 ≤ 4 – 3a ≤ 13
Answer:
The given inequality is:
-2 ≤ 4 – 3a ≤ 13
Subtract 4 on both sides
-2 – 4 ≤ 4 – 4 – 3a ≤ 13 – 4
-6 ≤ -3a ≤ 9
Divide by – on both sides
6 ≥ 3a ≥ -9
Divide by 3 on both sides
(6 / 3) ≥ (3a / 3) ≥ (-9 / 3)
2 ≥ a ≥ -3
-3 ≤ a ≤ 2
Hence, from the above,
We can conclude that the solution to the given inequality is -3 ≤ a ≤ 2
The representation of the solution of the inequality in the graph is:

Question 9.
-5 < 2 – h or 6h + 5 > 71
Answer:
The given inequality is:
-5 < 2 – h or 6h + 5 > 71
-5 – 2 < h or 6h > 71 – 5
-7 < -h or 6h > 66
7 < h or h > 66 / 6
h > 7 or h > 11
Hence, from the above,
We can conclude that the solution to the given inequality is h > 7 [Since h > 11 is before  h > 7]
The representation of the solution of the given inequality in the graph is:

Question 10.
| 2q + 8 | > 4
Answer:
The given absolute value inequality is:
| 2q + 8 | > 4
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
2q + 8 > 4 or 2q + 8 < -4
2q > 4 – 8 or 2q < -4 – 8
2q > -4 or 2q < -12
We know that,
The value of the absolute value expression must be greater than or equal to 0
Hence, from the above,
We can conclude that the given absolute value inequality has no solution

Question 11.
-2 | y – 3 | – 5 ≥ -4
Answer:
The given absolute value inequality is:
-2 | y – 3 | – 5 ≥ -4
So,
-2 | y – 3 | ≥ -4 + 5
-2 | y – 3 | ≥1
| y – 3 | ≥ –\(\frac{1}{2}\)
We know that,
The value of the absolute value expression must be greater than or equal to 0
Hence, from the above,
We can conclude that the given absolute inequality has no solution

Question 12.
4 | -3b + 5 | – 9 < 7
Answer:
The given absolute value inequality is:
4 | -3b + 5 | – 9 < 7
So,
4 | -3b + 5 | < 7 + 9
4 | -3b + 5 | < 16
| -3b + 5 | < 16 / 4
| -3b + 5 | < 4
We know that,
| x | = x for x > 0
| x | = -x for x < 0
So,
-3b + 5 < 4 and -3b + 5 > -4
-3b < 4 – 5 and -3b > -4 – 5
-3b < -1 and -3b > -9
3b < 1 and b > 3
b < \(\frac{1}{3}\) and b > 3
b < 0 and b > 3 [ Approximate value of inequality ]
Hence, from the above,
We can conclude that the solutions of the given inequality are b < 0 and b > 3
The representation of the solutions of the given inequality in the graph is:

Question 13.
You start a small baking business, and you want to earn a profit of at least $250 in the first month. The expenses in the first month are $155. What are the possible revenues that you need to earn to meet the profit goal?
Answer:
The possible revenues that you need to earn to meet the profit goal is:
R ≥ $405

Explanation:
It is given that you start a small baking business, and you want to earn a profit of at least $250 in the first month. The expenses in the first month are $155.
Now,
Let
P is the profit
R is the Revenue
E is the expenses
We know that,
P = R – E
It is given that P ≥ $250
So,
R – E ≥250
R – 155 ≥ 250
R ≥ 250 + 155
R ≥ 405
Hence, from the above,
We can conclude that the possible revenues that you need to earn to meet the profit goal is:
R ≥ $405

Question 14.
A manufacturer of bicycle parts requires that a bicycle chain have a width of 0.3 inches with an absolute deviation of at most 0.0003 inches. Write and solve an absolute value inequality that represents the acceptable widths.

Answer:
The absolute value inequality that represents the acceptable widths is:
0.2997 inches ≤ w ≤0.3003 inches

Explanation:
It is given that a manufacturer of bicycle parts requires that a bicycle chain have a width of 0.3 inches with an absolute deviation of at most 0.0003 inches.
We know that,
Absolute deviation = Mean – Observation
Let the Mean be x
So,
x – 0.3 ≤ 0.0003
Hence,
The absolute value inequality that represents the acceptable widths is:
| x – 0.3 | ≤ 0.0003
-0.0003 ≤ x – 0.3 ≤ 0.0003
Add with 0.3 on both sides
-0.0003 + 0.3 ≤ x – 0.3 + 0.3 ≤ 0.0003 + 0.3
0.2997 ≤ x ≤ 0.3003
Hence, from the above,
We can conclude that the absolute value inequality that represents the acceptable widths is:
0.2997 inches ≤ w ≤0.3003 inches

Question 15.
Let a, b, c, and d be constants. Describe the possible solution sets of the inequality ax + b < cx + d.
Answer:

Write and graph a compound inequality that represents the numbers that are not solutions to the inequality represented by the graph shown. Explain your reasoning.

Question 16.

Answer:
The given graph is:

From the graph,
The 1st marked line starts from -3 including -3 and continued till the left end of the number line
The 2nd marked line starts from 2 excluding 2 and continued till the right end of the number line
Hence,
The representation of the inequalities from the graph is:
x ≤ -3 and x > 2

Question 17.

Answer:
The given graph is:

From the graph,
The marked line starts from -4 including -4 and continued till -1 including -1 to the right end of the number line
Hence,
The representation of the inequality from the graph is:
x ≥ -4 and x ≤ -1
Hence,
The representation of the inequalities in the form of compound inequality is:
–4 ≤ x ≤ -1

Question 18.
A state imposes a sales tax on items of clothing that cost more than $175. The tax applies only to the difference in the price of the item and $175.
a. Use the receipt shown to find the tax rate (as a percent).
b. A shopper has $430 to spend on a winter coat. Write and solve an inequality to find the prices p of coats that the shopper can afford. Assume that p ≥ 175.
c. Another state imposes a 5% sales tax on the entire price of an item of clothing. For which prices would paying the 5% tax to be cheaper than paying the tax described above? Write and solve an inequality to find your answer and list three prices that are solutions.

Answer:
a.
From the given receipt,
The price is: $295
The total price is: $302.50
It is given that
Tax = Product price – $175
Now,
Let R be the tax rate
So,
R (product price – 175) = 7.5
R ( 295 – 175 ) = 7.5
R ( 120 ) = 7.5
%R = \(\frac{7.5}{120}\) × 100
%R = \(\frac{75}{1200}\) × 100
%R = 0.0625 × 100
%R = 6.25%
Hence, from the above,
We can conclude that the tax rate using the receipt is: 6.25%

b.
It is given that a shopper has $430 to spend on a winter coat
Let p be the number of coats
It is also given that to assume p ≥ 175
We know that,
The total price = The given price + Tax
So,
The representation of the inequality that represents the price of coats is:
p + R ( p – 175 ) ≤ 430
p + 0.0625 (p – 175)  ≤ 430
1.0625p – 10.9375 ≤ 430
1.0625p ≤ 430 + 10.9375
1.0625p ≤ 440.9375
p ≤ 440.9375 / 1.0625
p ≤ 415
Hence, from the above,
We can conclude that the prices of the coats that the shopper can afford are:
p ≤ $415

c.
It is given that another state imposes a 5% sales tax on the entire price of an item of clothing.
Now,
Let t be the tax rate that another state-imposed
Let x be the price
So,
(1+0.05) × t ≤ t + 0.0625 (t – 175)
1.05t ≤ 1.0625t – 10.9375
10.9375 ≤ 1.0625t – 1.05t
10.9375 ≤ 0.0125t
10.9375 / 0.0125 ≤ t
875 ≤ t
t ≥ 875
hence, from the above,
We can conclude that $875 is cheaper

Solving Linear Inequalities Maintaining Cumulative Assessment

Question 1.
The expected attendance at a school event is 65 people. The actual attendance can vary by up to 30 people. Which equation can you use to find the minimum and maximum attendances?
A. | x – 65 | = 30
B. | x + 65 | = 30
C. | x – 30 | = 65
D. | x + 30 | = 65
Answer:
It is given that the expected attendance at a school event is 65 people. The actual attendance can vary by up to 30 people.
So,
The absolute value equation that represents the maximum and minimum attendances are:
| x – Expected maximum attendance | ≤ 30
Hence,
| x – 65 | ≤ 30
| x – 65 | = 30
Hence, from the above,
We can conclude that option A represents the minimum and maximum attendances at a school event

Question 2.
Fill in values for a and b so that each statement is true for the inequality ax + 4 ≤ 3x + b.
a. When a = 5 and b = _____, x ≤ -3.
b. When a = _____ and b = _____, the solution of the inequality is all real numbers.
c. When a = _____ and b = _____, the inequality has no solution.
Answer:
The given inequality is:
ax + 4  ≤ 3x + b
a.
When a = 5,
5x + 4 ≤ 3x + b
5x – 3x + 4 ≤ b
2x + 4 ≤ b
2x ≤ b – 4
x ≤ ( b – 4 ) / 2
So,
The solution x ≤ -3 will be possible only if b = -2

b.
The given inequality is:
ax + 4 ≤ 3x + b
Compare the like coefficients
Hence,
The values of a and b so that the solution of an inequality is all real numbers are:
a = 3, b ≥ 4

c.
The given inequality is:
ax + 4 ≤ 3x + b
Hence,
The values of a and b so that the inequality has no solution are:
a = 3 and b < 4

Question 3.
Place each inequality into one of the two categories.

Answer:
The inequalities that have at least one integer solution must have x variable
The inequalities that have no integer solution must not have x variable
So,
The given inequalities are:
a. 5x – 6 + x ≥ 2x – 8
b. x – 8 + 4x ≤ 3 (x – 3) + 2x
c. 2 (3x + 8) > 3 (2x + 6)
d. 9x – 3 < 12 or 6x + 2 > -10
e. 17 < 4x + 5 < 21
f. 5 (x – 1) ≤ 5x – 3
Hence, from the above,
We can conclude that
The inequalities that have at least one integer solution are: a, d, e
The inequalities that have no integer solution are: b, c, f

Question 4.
Admission to a play costs $25. A season pass costs $180.
a. Write an inequality that represents the number x of plays you must attend for the season pass to be a better deal.
b. Select the number of plays for which the season pass is not a better deal.

Answer:
a.
It is given that admission to a play costs $25 and a season pass costs $180
Let the number of plays be x
So,
The total number of pays = 25x
Hence,
The inequality that represents the number x of plays you must attend for the season pass to be a  better deal is:
25x > 180
x > 180 / 25
x > 7.2
Hence, from the above,
We can conclude that the inequality that represents the number x of plays you must attend for the season pass to be a better deal is:
x > 7.2

b.
From part (a),
The inequality that represents the season pas to be a better deal is:
x > 7.2
So,
The inequality that represents the season pass not to be a better deal is:
x < 7.2
Hence, from the given numbers,
The number of plays that the season pass is not a better deal is: 0, 1, 2, 3, 4, 5, 6, and 7

Question 5.
Select the values of a that make the solution of the equation 3(2x – 4) = 4(ax – 2) positive.

Answer:
The given equation is:
3 (2x – 4) = 4 (ax – 2)
So,
3 (2x) – 3 (4) = 4 (ax) – 4 (2)
6x – 12 = 4ax – 8
6x – 12 + 8 = 4ax
6x – 4 = 4ax
6x – 4ax = 4
x (6 – 4a) = 4
Now,
The given numbers are: -2, -1, 0, 1, 2, 3, 4, 5
So,
x (6 – 4(-2) ) = 4
x ( 6 – 4 ( -1) ) = 4
x ( 6 – 4(0) ) = 4
x ( 6 – 4(1) ) = 4
x ( 6 – 4 (2) ) = 4
x ( 6 – 4 (3) ) = 4
x ( 6 – 4 (4) ) = 4
x ( 6 – 4 (5) ) = 4
Hence, from the above,
We can conclude that the values of a so that the solution is positive are: -2, -1, 0, 1

Question 6.
Fill in the compound inequality with <, ≤, , ≥, or > so the solution is shown in the graph.

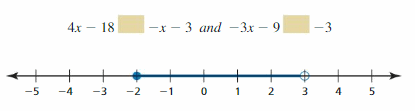
Answer:
From the graph,
The representation of the inequality is:
-2 ≤ x < 3
Now,
The given inequality is:
4x – 18 ____ -x – 3 and -3x – 9 _____ -3
4x + x ____ -3 + 18 and -3x ___ -3 + 9
5x ____ 15 and -3x ___ 6
x ____ 15 / 5 and x ____ -3 / 6
x ____ 3 and x ____ -2
Hence,
The blanks that can fill the inequality are:
x < 3 and x ≥ -2

Question 7.
You have a $250 gift card to use at a sporting goods store.

a. Write an inequality that represents the possible numbers x of pairs of socks you can buy when you buy 2 pairs of sneakers. Can you buy 8 pairs of socks? Explain.
b. Describe what the inequality 60 + 80x ≤ 250 represents in this context.
Answer:
a.
It is given that
The cost of a pair of sneakers is: $80
The cost of a pair of socks is: $12
It is given that there are 2 pairs of sneakers and x pairs of socks
Hence,
The inequality that represents the possible number of x pairs of socks you can buy when you buy 2 pairs of sneakers is:
2 (80) + 12x ≤ 250
160 + 12x ≤ 250
12x ≤ 250 – 160
12x ≤ 90
x ≤ 90 / 12
x ≤ 7.5
Hence, from the above,
We can conclude that you can buy only 7 pairs of socks

b.
The given inequality is:
60 + 8x ≤ 250
12 (5) + 8x ≤ 250
Hence, from the above,
We can conclude that you can buy 5 pairs of sneakers in this context

Question 8.
Consider the equation shown, where a, b, c, and d are integers.
ax + b = cx + d
Student A claims the equation will always have one solution. Student B claims the equation will always have no solution. Use the numbers shown to answer parts (a)–(c).

a. Select values for a, b, c, and d to create an equation that supports Student A’s claim.
Answer:
The given equation is:
ax + b = cx + d
Student A claims the equation will have always one solution
Hence,
From the given numbers,
The values of a, b, c, and d are:
a = -1, b = 2, c = -1, d = 4
So,
The value of x is:
-x + 2 = x + 4
-x – x = 4 – 2
-2x = 2
x = -2 /2
x = -1
Hence, from the above,
We can conclude that according to Student A’s claim,
The values of a, b, c, and d are:
a = -1, b = 2, c = 1, d = 4

b. Select values for a, b, c, and d to create an equation that supports Student B’s claim.
Answer:
The given equation is:
ax + b = cx + d
Student B claims that the equation will have no solution
So,
The value of x must be equal to 0
So,
a must be equal to c
Hence,
The values of a, b, c, and d are: a = c and the values of b and d will be any number from the given numbers

c. Select values for a, b, c, and d to create an equation that shows both Student A and Student B are incorrect.
Answer:
The given equation is:
ax + b = cx + d
For the claims of both Student A and Student B to be false,
The given equation must have the real numbers as a solution
So,
To have the real numbers as a solution, the values of a and b will be arbitrary from the given numbers