The Area and Perimeter of the Rhombus are used in the basic Mensuration. In order to find the area and perimeter students must know what are the properties of the Rhombus. Here we explain the properties, formulas with examples. A rhombus is a quadrilateral which is similar to the parallelogram. The shape of the Rhombus looks like a diamond.
In this article, students can learn how to calculate the area and perimeter of the Rhombus. We have provided multiple examples to make the students understand the concept of Perimeter and Area of Rhombus. So, learn different methods to find the area and perimeter of the rhombus.
What is Area and Perimeter of a Rhombus?
Area of Rhombus – The area of the Rhombus is the space occupied by the two-dimensional figure. The Area of Rhombus Formula is equal to half of the product of two diagonals. The area of the rhombus is measured in square units.
- A = 1/2(d1 × d2) sq. units
where d1 and d2 are diagonals of the rhombus.
Perimeter of Rhombus – The perimeter of the rhombus is the sum of lengths of the boundaries. The Perimeter of the Rhombus Formula is equal to the sum of four sides. The perimeter of the Rhombus is measured in units.
- P = a + a + a + a = 4a units
Where a is the side of the rhombus.
Properties of Rhombus
The properties of the rhombus are given below
- All the sides of the rhombus are equal.
- It consists of 4 vertices and 4 edges.
- Opposite angles of the rhombus are the same.
- The sum of the adjacent angles is 180 degrees.
- In Rhombus the diagonals bisect the angles.
- Opposite sides of the rhombus are parallel.
Solved Examples on Area and Perimeter of a Rhombus
Go through the below section to know where and how to use the area and perimeter of the rhombus problems.
1. Find the area of the rhombus if the diagonals are 7m and 5m.
Solution:
Given,
d1 = 7m
d2 = 5m
We know that,
Area of the Rhombus = 1/2(d1 × d2)
A = 1/2(7m × 5m)
A = 35/2
A = 17.5 m²
Therefore the area of the rhombus is 17.5 sq. meters.
2. The area of the rhombus is 196 sq. cm. One of the diagonal is 14 cm find the other diagonal?
Solution:
Given,
The area of the rhombus is 169 sq. cm.
d1 = 14 cm
d2 = ?
We know that,
Area of the Rhombus = 1/2(d1 × d2)
196 sq. cm = 1/2 (14 cm × d2)
196 sq. cm = 7 cm × d2
d2 = 196/7 = 28 cm
Thus the length of the another diagonal is 28 cm.
3. What is the perimeter of the rhombus if the side is 6cm?
Solution:
Given,
a = 6 cm
We know that,
The perimeter of the Rhombus = 4a
P = 4(6 cm)
P = 24 cm
Thus the perimeter of the rhombus is 24 cm.
4. Find the area of the rhombus whose sides are 8 cm and diagonal is 6 cm?
Solution:
Given,
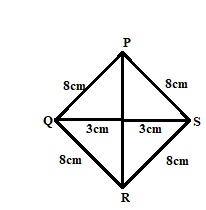
PQ = QR = RS = PS = 8 cm
QS = 6 cm
In ΔPOQ,
PQ² = OQ² + OP²
8² = 3² + OP²
64 = 9 + OP²
OP² = 64 – 9
OP² = 55
OP = 7.4
PR = 2OP
PR = 7.4 × 7.4
PR = 54.76
Area of the Rhombus = 1/2(d1 × d2)
A = 1/2 (6 × 54.76)
A = 164.28 sq. cm
Therefore the area of the rhombus is 164.28 sq. cm.
5. If the perimeter of the rhombus is 52 cm then find the side of the rhombus?
Solution:
Given,
the perimeter of the rhombus is 52 cm
We know that,
Perimeter of Rhombus = 4a
52 cm = 4a
a = 52/4
a = 13 cm
Thus the side of the rhombus is 13 cm.
6. Find the height of the rhombus whose area is 169 sq. m and perimeter is 140 m?
Solution:
Given that
P = 140 m
P = 4a
140 = 4a
a = 140/4
a = 35
Now use the area of the rhombus to find the height.
169 sq. m = 35 × h
h = 169/35
h = 4.82 m
Thus the height of the rhombus is 4.82 meters.
FAQs on Area and Perimeter of Rhombus
1. What are the basic properties of the Rhombus?
- Opposite sides are equal
- The sum of the adjacent angles is 180 degrees
- All sides are equal in Rhombus.
2. How to find the perimeter of the rhombus?
The perimeter of the rhombus can be calculated by adding all four sides.
3. Is the area of the rhombus and square is the same?
The length of the rhombus is the same but the area of the square and rhombus are not equal.