If two straight lines coincide at a point, then it is called the angle. The angle of elevation is defined as the angle between the horizontal plane and oblique line from the observer’s eye to an object which is located above his eye. Finally, the angle formed above the surface. It is a widely used concept and it is related to height and distance. The different terms used in the angle of elevation concept, trigonometric formulas, and solved examples are mentioned below for the sake of students.
Angle of Elevation – Definition
The angle of elevation of an object seen by the observer is the angle formed between the horizontal and the line from the object to the observer’s eye. The line in which the observer’s eye is there is known as the line of sight.
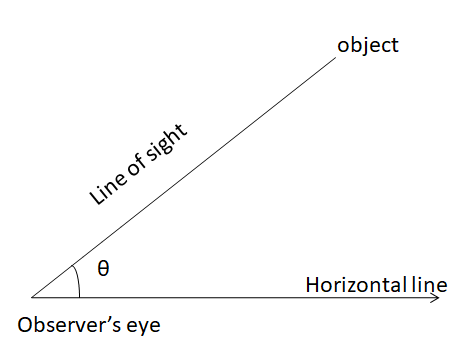
From the above image, you can see that the observer is looking at the object from the ground making an angle θ with the line of sight and horizontal line. By joining the imaginary line between the object and the end of the horizontal line, it forms a right-angle triangle. Thus we can use the trigonometry concept to find the distance from the observer to the object.
Example:
A student named Rakesh is looking at a bird sitting at the building, then there is an angle formed, which is inclined towards the bird from the Rakesh eye. This elevation angle is helpful to find the distance, height of the building with the trigonometric function like sine, cosine, and tangent.
Terms used in Elevation Angle
The three most important terms used in this concept are angle, horizontal line, and line of sight. Let us discuss each of them in detail in the following sections.
Horizontal Line:
A straight line on the flat surface where all points lie on a line and those points will have the same y-coordinate value. The angle and horizontal lines combine to form the angle of elevation.
Angle:
If two line segments meet at an endpoint, then the point is called the vertex. When two straight lines meet at a common point form an angle. It is also defined as the gap between two limes that connect on one side. It is measured in degrees or radians.
Line of Sight:
The line which is drawn from the observer’s eye to the object is known as the line of sight. In the angle of elevation, the object is kept above the line of sight of the observer. If you know the elevation angle, then it is easy to determine the distance and altitude.
Also, Check:
Angle of Elevation Formulas
Trigonometric ratios are used to find the unknown measures of the opposite, adjacent, and hypotenuse sides of the right angle.
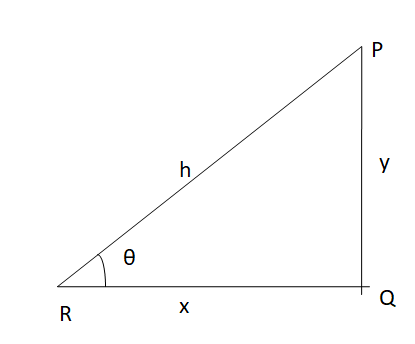
The trigonometric ratios are
sin θ = \(\frac { Opposite side }{ Hypotenuse } =\frac { y }{ h } \)
cos θ = \(\frac { Hypotenuse }{ Adjacent side } =\frac { h }{ x } \)
tan θ = \(\frac { Opposite side }{ Adjacent side } =\frac { x }{ y } \)
Another type of problem is along the lines.
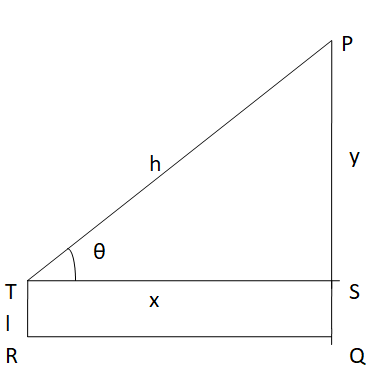
PQ = y, TQ = SR = I, PT = (y – l), QR = ST = x, PS = h
The formulas are
sin θ = \(\frac { PT }{ PS } =\frac { y – l }{ h } \)
cos θ = \(\frac { QR }{ PS } =\frac { x }{ h } \)
tan θ = \(\frac { PT }{ QR } =\frac { y – l }{ x } \)
Angle of Elevation Problems
Example 1:
A tower stands vertically on the ground. From a point on the ground, which is 48 m away from the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower.
Solution:
Let AB be the height of the tower.
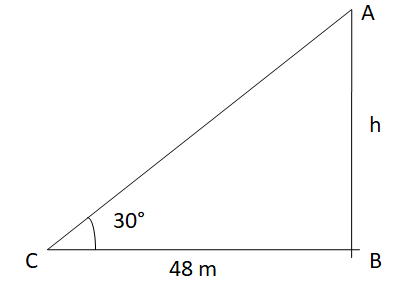
Take AB = h and BC is the distance between the tower and the point C. In the right-angled trinagle ABC, ∠ACB = 30°
tan θ = \(\frac { AB }{ BC } \)
tan 30 = \(\frac { h }{ 48 } \)
\(\frac { 1 }{ √3 } \) = \(\frac { h }{ 48 } \)
cross multiply the fractions
48 = h√3
h = \(\frac { 48 }{ √3 } \)
h = 16√3
Therefore, the height of the tower is 16√3 m
Example 2:
A ladder of length 20 m is kept in against a wall of length 15 m such that their topmost point is in contact with one another and their bottom point is at a certain distance as shown in the figure. Find the angle subtended by the ladder on the floor.
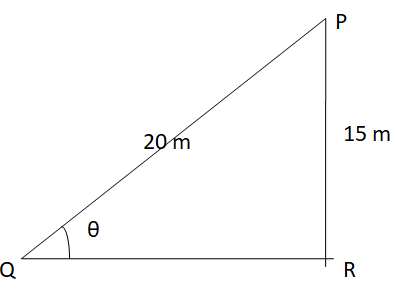
Solution:
The length of the ladder is PQ = 20 m
The height of the wall is PR = 15 m
We have to find angle PQR = angle subtended by the ladder on the floor.
Let angle PQR = θ
We know that,
sin θ = \(\frac { PR }{ PQ } \)
sin θ = \(\frac { 15 }{ 20 } \)
θ = sin-1 (\(\frac { 15 }{ 20 } \))
θ = sin-1 (\(\frac { 3 }{ 4 } \))
θ = 48.59°
The angle subtended by the ladder on the floor is 48.59°.
Example 3:
A man of height 1 m 30 cm is standing in front of a tree of height 30 m. Find the angle of elevation to be made by the man’s eyes to look at the topmost point of the tree if the man is standing at a distance of 5 m from the tree.
Solution:
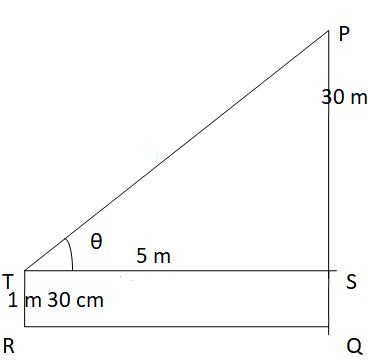
Here, PQ is the height of the tree = 30m
TR is the height of man = 1 m 30 cm = 1.30 m
RQ is the distance between the foot of the man and the tree = ST = 5 m
We have to find the angle of elevation, θ =?
We know that,
tan θ = \(\frac { (30 – 1.30) }{ 5 } \)
tan θ = 5.74
θ = tan-1 (5.74)
θ = 80.117°
The angle of elevation to be made by the man’s eye is 80.117°.
Example 4:
When the angle of elevation of the Sum is 45°, the shadow of a coconut tree is 15 m in length. What is the height of the coconut tree?
Solution:
Let AB denote the height of the coconut tree and BC denotes the length of the shadow.
Therefore, according to the problem ∠ACB = 45°, BC = 18 m.
Let the height of the coconut tree AB = x meters.
Now, tan 45° = \(\frac { AB }{ BC } \)
1 = \(\frac { x }{ 18 } \)
x = 18
Therefore, the height of the coconut tree is 18 meters.
FAQs on Angle of Elevation
1. What is the angle of elevation in trigonometry?
The angle of elevation is the angle between the horizontal line of the sight and the line of sight up to an object.
2. Differences between the angle of elevation and depression?
The angle of depression is opposite to the angle of elevation. In the angle of depression, the observer is standing at the height and the object is placed below the line of sight of the observer.
3. What is the formula for Angle of Elevation?
The formula for Angle of Elevation is given by
sin θ = \(\frac { Opposite side }{ Hypotenuse } =\frac { y }{ h } \)
cos θ = \(\frac { Hypotenuse }{ Adjacent side } =\frac { h }{ x } \)
tan θ = \(\frac { Opposite side }{ Adjacent side } =\frac { x }{ y } \)
