Addition and Subtraction of Unlike Fractions are different compared to the addition and subtraction of the like fractions. The, unlike fractions, are fractions that have different denominators. It is a bit difficult to add or subtract, unlike fractions compared to like fractions. But if you go through this entire article, you will find the easy way to learn addition and subtraction of unlike fractions.
Different ways have been given to solve the unlike fractions with solved examples and images. Learn the addition and subtraction of Unlike Fractions by referring to the entire article. You can get all the 6th Grade Math Concepts and their worksheets on our website. Also, take the practice sessions and cross-check your answers for the best practice. We have given the best way of learning for students with our concepts.
Also, find:
How to Add Unlike Fractions? | Adding Fractions with Unlike Denominators
The addition of unlike fractions is the process of adding fractions having different denominators. Check out the addition of unlike fractions with the following procedure.
1. Firstly, take the given fractions with their denominators.
2. Then, take the LCM of the given unlike fractions. Or you can also take the cross multiplication of fractions.
3. Convert the unlike fractions into like fractions.
4. Finally, add the like fractions and write down the final answer.
Addition of Unlike Fractions Examples
We have given different problems along with their explanation and answers. Go through the all problems and learn the complete concept clearly.
Question 1. \(\frac { 3 }{ 2 } \) + \(\frac { 3 }{ 4 } \)
Solution: Given fractions are \(\frac { 3 }{ 2 } \) and \(\frac { 3 }{ 4 } \).
Convert the unlike fractions into like fractions.
Take the LCM of 2 and 4.
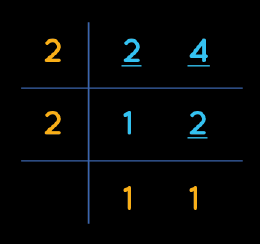
The LCM of 2 and 4 is 4.
Now, multiply and divide the fraction \(\frac { 3 }{ 2 } \) with 2 which is equal to \(\frac { 6 }{ 4 } \).
Multiply and divide the fraction \(\frac { 3 }{ 4 } \) with 1 which is equal to \(\frac { 3 }{ 4 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 4.
Add both like fractions.
\(\frac { 6 }{ 4 } \) + \(\frac { 3 }{ 4 } \) = \(\frac { 10 }{ 4 } \)
Therefore, the final answer is \(\frac { 10 }{ 4 } \).
Question 2.
\(\frac { 2 }{ 6 } \) + \(\frac { 6 }{ 8 } \)
Solution:
Given fractions are \(\frac { 2 }{ 6 } \) and \(\frac { 6 }{ 8 } \).
Convert the unlike fractions into like fractions.
Take the LCM of 6 and 8.
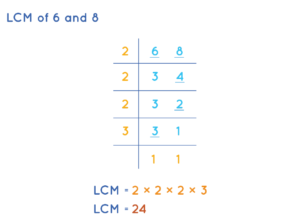
The LCM of 6 and 8 is 24.
Now, multiply and divide the fraction \(\frac { 2 }{ 6 } \) with 4 which is equal to \(\frac { 8 }{ 24 } \).
Multiply and divide the fraction \(\frac { 6 }{ 8 } \) with 3 which is equal to \(\frac { 18 }{ 24 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 24.
Add both like fractions.
\(\frac { 8 }{ 24 } \) + \(\frac { 18 }{ 24 } \) = \(\frac { 26 }{ 24 } \)
Therefore, the final answer is \(\frac { 26 }{ 24 } \).
Question 3. Add 2 \(\frac { 3 }{ 4 } \) and 3 \(\frac { 2 }{ 5 } \)
Solution: Given fractions are 2 \(\frac { 3 }{ 4 } \) and 3 \(\frac { 2 }{ 5 } \).
Firstly, convert the mixed fractions into fractions.
2 \(\frac { 3 }{ 4 } \) = \(\frac { 11 }{ 4 } \)
3 \(\frac { 2 }{ 5 } \) = \(\frac { 17 }{ 5 } \)
Convert the unlike fractions into like fractions.
Take the LCM of 4 and 5.
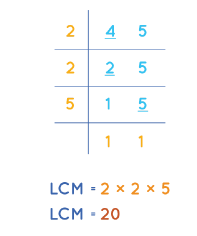
The LCM of 4 and 5 is 20.
Now, multiply and divide the fraction \(\frac { 11 }{ 4 } \) with 5 which is equal to \(\frac { 55 }{ 20 } \).
Multiply and divide the fraction \(\frac { 17 }{ 5 } \) with 4 which is equal to \(\frac { 68 }{ 20 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 20.
Add both like fractions.
\(\frac { 55 }{ 20 } \) + \(\frac { 68 }{ 20 } \) = \(\frac { 123 }{ 20 } \)
Therefore, the final answer is \(\frac { 123 }{ 20 } \).
How to Subtract Unlike Fractions?
The subtraction of unlike fractions is completely different compared to subtraction of like fractions which are having different denominators. Check out the subtraction of unlike fractions with the following procedure.
1. Firstly, take the given fractions with their denominators.
2. Then, take the LCM of the given unlike fractions. Or you can also take the cross multiplication of fractions.
3. Convert the unlike fractions into like fractions.
4. Finally, Subtract the like fractions and write down the final answer.
Subtracting Unlike Fractions Examples
We have given different problems along with their explanation and answers. Go through the all problems and learn the complete concept clearly.
Question 1. Find the difference of \(\frac { 4 }{ 6 } \) and \(\frac { 3 }{ 9 } \)
Solution: Given fractions are \(\frac { 4 }{ 6 } \) and \(\frac { 3 }{ 9 } \).
Convert the unlike fractions into like fractions.
Take the LCM of 6 and 9.
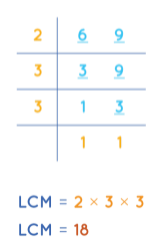
The LCM of 6 and 9 is 18.
Now, multiply and divide the fraction \(\frac { 4 }{ 6 } \) with 3 which is equal to \(\frac { 12 }{ 18 } \).
Multiply and divide the fraction \(\frac { 3 }{ 9 } \) with 2 which is equal to \(\frac { 6 }{ 18 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 18.
Subtract both like fractions.
\(\frac { 12 }{ 18 } \) – \(\frac { 6 }{ 18 } \) = \(\frac { 6 }{ 18 } \)
Therefore, the final answer is \(\frac { 6 }{ 18 } \).
Question 2. Find the difference of \(\frac { 17 }{ 12 } \) and \(\frac { 15 }{ 8 } \)
Solution: Given fractions are \(\frac { 17 }{ 12 } \) and \(\frac { 15 }{ 8 } \).
Convert the unlike fractions into like fractions.
Take the LCM of 12 and 8.
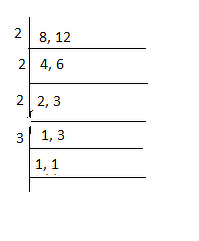
The LCM of 8 and 12 is 24.
Now, multiply and divide the fraction \(\frac { 17 }{ 12 } \) with 2 which is equal to \(\frac { 34 }{ 24 } \).
Multiply and divide the fraction \(\frac { 15 }{ 8 } \) with 3 which is equal to \(\frac { 45 }{ 24 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 24.
Subtract both like fractions.
45 is greater than 34. Therefore subtract \(\frac { 34 }{ 24 } \) from \(\frac { 45 }{ 24 } \).
\(\frac { 45 }{ 24 } \) – \(\frac { 34 }{ 24 } \) = \(\frac { 11 }{ 24 } \)
Therefore, the final answer is \(\frac { 11 }{ 24 } \).
Question 3. Find the difference of 2 \(\frac { 3 }{ 4 } \) and 3 \(\frac { 2 }{ 5 } \)
Solution: Given fractions are 2 \(\frac { 3 }{ 4 } \) and 3 \(\frac { 2 }{ 5 } \).
Firstly, convert the mixed fractions into fractions.
2 \(\frac { 3 }{ 4 } \) = \(\frac { 11 }{ 4 } \)
3 \(\frac { 2 }{ 5 } \) = \(\frac { 17 }{ 5 } \)
Convert the unlike fractions into like fractions.
Take the LCM of 4 and 5.

The LCM of 4 and 5 is 20.
Now, multiply and divide the fraction \(\frac { 11 }{ 4 } \) with 5 which is equal to \(\frac { 55 }{ 20 } \).
Multiply and divide the fraction \(\frac { 17 }{ 5 } \) with 4 which is equal to \(\frac { 68 }{ 20 } \).
Now, two unlike fractions converted to like fractions with the same denominator of 20.
Subtract both like fractions.
68 is greater than 55. Therefore subtract \(\frac { 55 }{ 20 } \) from \(\frac { 55 }{ 20 } \).
\(\frac { 68 }{ 20 } \) – \(\frac { 55 }{ 20 } \) = \(\frac { 13 }{ 20 } \)
Therefore, the final answer is \(\frac { 13 }{ 20 } \).
FAQs on Adding and Subtracting Unlike Fractions
1. What is an Unlike Fraction with Example?
An unlike fraction can defined as the fractions consisting of different denominators. That means the fractions having different number in the denominator are called as the unlike fractions. Examples of Unlike fractions are \(\frac { 1 }{ 3 } \), \(\frac { 3 }{ 6 } \), \(\frac { 4 }{ 7 } \).
2. How to Add Unlike Fractions?
To add Unlike fractions, convert the unlike fractions to like fractions. Then, just add their numerators and note down the sum as the addition of numerators over the common denominator. For example, 3/10 + 4/5 = (3 + 8)/10 = 11/10.
3. How to Subtract Unlike Fractions?
To subtract Unlike fractions, convert the unlike fractions to like fractions. Then, just subtract their numerators and note down the subtraction as the subtraction of numerators over the common denominator. For example, 5/4 – 3/8 = (10 – 3)/8 = 7/8.
4. How to covert unlike fractions into like fractions?
There are two simple ways available to convert unlike fractions into like fractions. They are the LCM method and cross multiplication method. You can choose any one of the methods to convert the unlike fractions into like fractions. Then, you can easily perform arithmetic operations like addition and subtraction, etc.
