Spike Abacus is a manual tool to easily learn mathematical calculations using abacus base and beads. Also, it can help students in performing arithmetic operations on their own within seconds. Children show interest in mathematics by Learning through Abacus.
Spike Abacus has iron spikes on a wooden base, where every spike represents the place values like ones, tens, hundreds, and so on. The spike has beads to show the numbers given. You can make use of this abacus by performing math functions in different digits of numbers. Here, we will learn about 4-Digits Number on Spike Abacus and their representation on spikes. You can also know how to perform some arithmetic operations on 4-Digits Numbers using Abacus.
Read More:
What are Four-Digits Numbers?
Four-Digits numbers are from 1000 to 9999. The four-digit number comes by adding 1 to the greatest 3-digit number i.e., 1+999=1000. The smallest 4-digit number is 1000 and the greatest number is 9999. To know how many 4-digits numbers are there we subtract the greatest number from the smallest number of 4-digits, i.e., 9999-1000=8999.
Now, we add 1 to the resultant then we can know how many 4-digits numbers, i.e., 8999+1=9000. Thus, there are 9000 4-Digits Numbers. Let’s represent some of the four-digit numbers on the spike abacus base.
How to Represent 4-Digits Numbers using Spike Abacus?
To show 4-digits numbers on the spike abacus we use place values. The place values use for 4-digits numbers are thousands, hundreds, tens, and ones. The following image shows the spikes to represent 4-digit numbers.
4-Digits Numbers Representation Using Abacus Examples
( i ) 4123
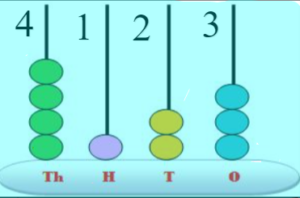
The number shown on the spike abacus base is 4123. In thousand place, there are 4 beads that say the number 4, in the hundreds place, there is 1 bead that says the number 1, in tens, there are 2 beads that say the number 2, and in one’s place there are 3 beads that say the number 3. The number says in words as four thousand, one hundred twenty-five.
( ii ) 4102
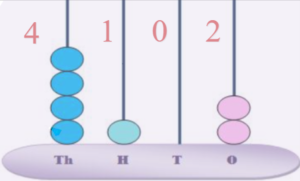
The number shown on spikes is 4102. In thousands place, there are 4 beads that show the number 4, in the hundreds place, there is 1 bead that shows the number 1, in the tens place, there are no beads that represents the number 0, in one’s place, there are 2 beads that show the number 2. Thus, the number in words is four thousand, one hundred, and two.
( iii ) 3245
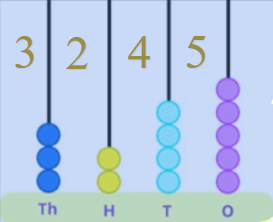
The number shown in the Abacus base is 3245. In the thousands place, we kept 3 beads that represent the number 3, in the hundreds place, we kept 2 beads that represent the number 2, in the tens place, we kept 4 beads that represent the number 4, and in one’s place, we kept 5 beads that represent the number 5. Thus, the number in words is three thousand, two hundred forty-five.
Addition of 4-Digits Number on Spike Abacus
To perform the addition of four-digit numbers on the abacus, we have to follow certain steps discussed below. Let’s take two numbers 3245, 2413 for addition. Below image is the representation of given 4-digit numbers on the Spike Abacus.
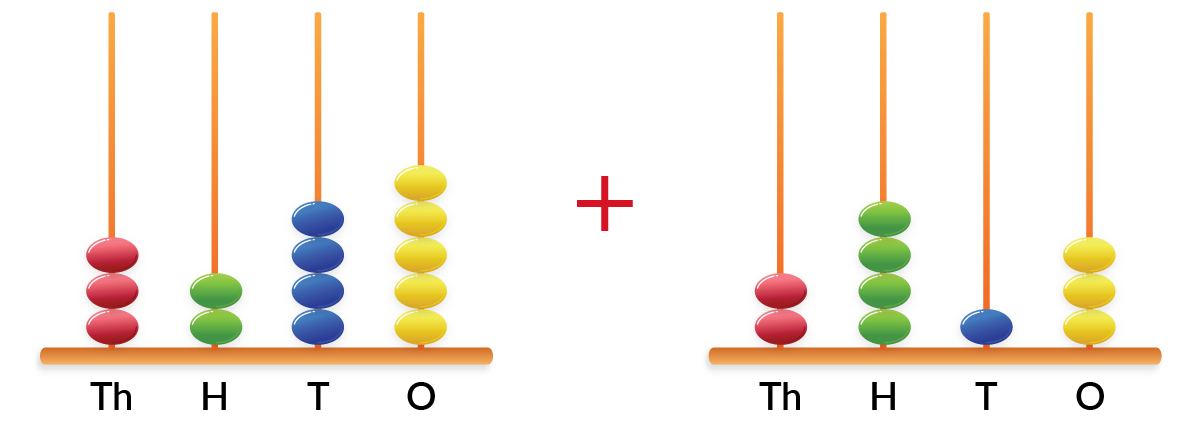
Step 1: Take the given numbers and notice the place values of two numbers
Step 2: Now, keep the beads in the place values of two given numbers in 2 spikes of the abacus.
Step 3: For the number 3245, keep 3 beads in Th, keep 2 beads in H, keep 4 beads in T, and keep 5 beads in O of the first spike of the abacus base. Then take the second number 2413, keep 2 beads in Th, keep 4 beads in H, keep 1 bead in T, and keep 3 beads in O of the second spike of the abacus base.
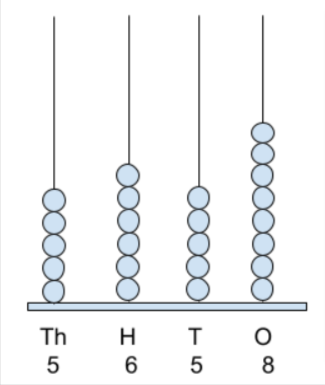
Step 4: Let’s add the same place values of both spikes to get the result of an addition of given numbers, i.e., in the thousands place ( 3+2=5 beads ), in the hundreds place ( 2+4=6 beads ), in the tens place ( 4+1=5 beads ), and in ones place (5+3=8 beads ). Thus, the addition of the given numbers is 5,658.
Step 5: Next, represent this resultant addition of 4-digits numbers 3245, 2413 ie., 5,658 using beads on Spike Abacus Base. Take a look at the below resultant representation.