By accessing our 180 Days of Math for Fifth Grade Answers Key Day 180 regularly, students can get better problem-solving skills.
180 Days of Math for Fifth Grade Answers Key Day 180
Directions: Solve each problem.
Question 1.
Subtract 85 from 152.
Answer:
Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 200 and we have given an Rs. 500 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 500 – 200 = 300. Then, the vendor will return Rs. 300.
Now we need to calculate the above-given question:
we need to subtract 85 from 152.
In the below subtraction, we need to make borrowing from the other number.
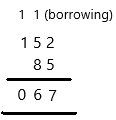
152 = Minuend; 85 = Subtrahend; 67 = Difference
Therefore, the answer is 67.
Question 2.
72 • 82 = ___________
Answer:
In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life. The major application we can see in multiplication tables.
In arithmetic, the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ number of times or vice versa.
The formula for multiplication:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– A multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
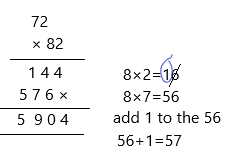
Therefore, 72. 82 is equal to 5904.
Question 3.
![]()
Answer:
The square root of a number is defined as the value, which gives the number when it is multiplied by itself. The radical symbol √ is used to indicate the square root. For example, √9 = 3. The radical symbol is also called a root symbol or surds. If a number is a perfect square, we can easily find the square root of the number. If the given number is not a perfect square number, the square root can be found using the long division method.
642 is not a perfect square.
– Here we will show you how to calculate the square root of 642 using the long division method with one decimal place accuracy.
step 1: Set up 642 in pairs of two digits from right to left and attach one set of 00 because we want one decimal:
![]()
step 2: Starting with the first set: the largest perfect square less than or equal to 6 is 4, and the square root of 4 is 2. Therefore, put 2 on top and 4 at the bottom like this:
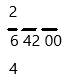
step 3: Calculate 6 minus 4 and put the difference below. Then move down the next set of numbers.
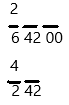
step 4: Double the number in green on top: 2 × 2 = 4. Then, use 4 and the bottom number to make this problem:
![]()
The question marks are “blank” and the same “blank”. With trial and error, we found the largest number “blank” can be is 5. Replace the question marks in the problem with 5 to get:
45 × 5 = 225.
Now, enter 5 on top, and 225 at the bottom:
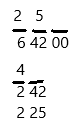
step 5: Calculate 242 minus 225 and put the difference below. Then move down the next set of numbers.
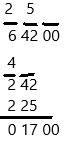
step 6: Double the number in green on top: 25 × 2 = 50. Then, use 50 and the bottom number to make this problem:
50? × ? ≤ 1700
The question marks are “blank” and the same “blank”. With trial and error, we found the largest number “blank” can be is 3. Now, enter 3 on top:
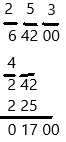
The answer is on top. The square root of 642 with one digit decimal accuracy is 25.3. Did you notice that the last two steps repeat the previous two steps? You can add decimals by simply adding more sets of 00 and repeating the last two steps over and over.
therefore, the square root of 642 is 25.3
The above-given question is 63 square root of 642 is:
We got a square root of 642 is 25.3
Now multiply 63 by 25.3
Thus, 63*25.3 is 1593.9
Question 4.
What is the value of the digit 6 in the number 694,205?
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The above-given number is 694,205.
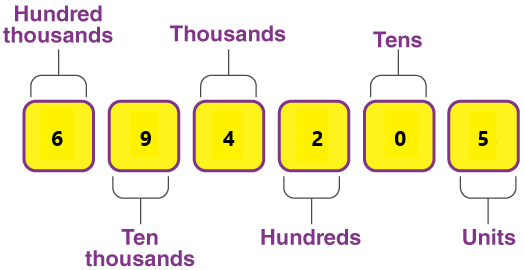
The place value of 6 is hundred thousand and the number is written in 600,000
Question 5.
\(\frac{3}{10}\) + \(\frac{1}{10}\) = ___________
Answer:
\(\frac{3}{10}\) is 3/10
\(\frac{1}{10}\) is 1/10
we need to add these values:
3/10+1/10
=4+1/10
=5/10
=1/2.
Therefore, \(\frac{3}{10}\) + \(\frac{1}{10}\) is 1/2.
Question 6.
20 × 3 – 99 ÷ 3 = ___________
Answer:
20 × 3 =60
99 ÷ 3 = 33
now subtract the values.
60-33=27
Therefore, 20 × 3 – 99 ÷ 3 is 27.
Question 7.
63 ÷ 9 = 56 ÷ 
Answer:
63 ÷ 9 = 56 ÷ 
why 8?
if we divide 63 by 9 then we get 7 as quotient and 0 as remainder.
If we divide 56 by 7 then we get 7 as quotient and 0 as remainder.
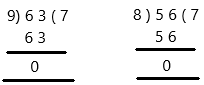
we got equal quotients and equal remainders.
so, 8 is the correct answer.
Question 8.
Calculate the perimeter of a pentagon with 3-cm sides.
Answer:
the perimeter of pentagon formula:
Using the perimeter of a pentagon formula, you can find the perimeter of a regular pentagon with relative ease. To find the perimeter of a regular pentagon with sides of length, s, you use this formula:
p=5×s
In our formula, 5 is the number of sides, and S is the length of the side that we know. Just like with the perimeter of a square, or the perimeter of a polygon in general, you find the perimeter of a pentagon by adding all the sides together.
– If you are finding the perimeter of a regular pentagon, then you know that all five sides are equal lengths, so you can simplify the formula using multiplication instead of addition. If you prefer to use the addition method your perimeter for a regular pentagon would look like this:
p=S+S+S+S+S
we know one side length is 3 cms then we can easily find the perimeter.
If we know one side of a regular pentagon, then we know the length of each side because a regular pentagon has equal sides. We can simply plug our known side into our formula:
p=5×3
p=15 cms
or we can do an addition:
p=5+5+5+5+5
p=15.
Question 9.
Are these squares congruent?
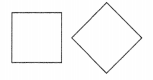
Answer:
Two congruent figures with one rotated. Two squares are congruent if they have the same side. But the second diagram is like a rhombus. A square and a rhombus are neither similar nor congruent. A congruent figure has exactly the same size and shape. Rhombus is a quadrilateral figure that is in the shape of a diamond with a flat shape with four equal straight sides.
Question 10.
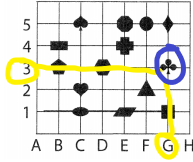
Name the shape that is located at (G, 3).
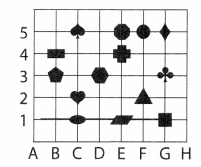
Answer:
First look at the alphabet G and go for the number 3.
The shape at (G, 3) is a tree shape which is called a taxon.
Question 11.
Your mom is baking you a birthday cake. You can choose chocolate or white cake. You can choose chocolate or vanilla frosting. How many different combinations of cake and frosting are there?
Answer:
The number of different combinations of baking birthday cake=2
The choices are chocolate and white cakes.
The number of different combinations of frosting=2
The frosting choices are chocolate and vanilla.
Question 12.
Factor wheels show all the factors of a number. Complete the factor wheel.
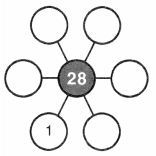
Answer:
The factors of 28 are the numbers that can evenly divide 28. These factors are 1,2,4,7,14 and 28. When we divide 28 by any of its factors, then the remainder will be equal to 0 and the quotient will be a natural number.
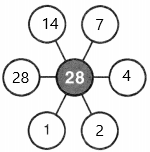
Suppose, 28 divided by 7 is equal to 4, thus 7 is one of the factors of 28.
28/7 = 4
Similarly, the pair factors are the set of numbers that on multiplication produces the original number. For example, 1 and 28 both are the factors of real number 28, since, 1 multiplied by 28 is equal to 28 itself.
1 x 28 = 28.