By accessing our 180 Days of Math for Fifth Grade Answers Key Day 148 regularly, students can get better problem-solving skills.
180 Days of Math for Fifth Grade Answers Key Day 148
Directions: Solve each problem.
Question 1.
187 – 55 = __________
Answer:
Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 200 and we have been given Rs. 500 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 500 – 200 = 300. Then, the vendor will return Rs. 300.
Now we need to calculate the above-given question:
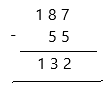
187 = Minuend; 55 = Subtrahend; 132 = Difference
Therefore, the answer is 132.
Question 2.
Colour the two factors that give the central product.
Answer:
to find the factors of 63 using division method is given below:
– Dividing 63 by 1 we get 63. (1 and 63 are the factors)
– Dividing 63 by 3 we get 21. (3 and 21 are the factors)
– Now we know 21 is also a composite number.
– Divide 21 by 3, we get 7 (Again 7 and 3 are the factors)
Hence, by the above steps, the numbers 1, 63, 21, 7 and 3 become the factors of 63. Since 3 is repeated twice, thus 3 x 3 = 9 is also a factor of 63. Therefore, the total factors are 1, 3, 7, 9, 21 and 63.
– The factors of 63 are the numbers that divide the number 63 exactly without leaving any remainder. In other words, the pair factors of 63 are the numbers that are multiplied in pairs resulting in the original number 63. Since the number 63 is a composite number, 63 has more than two factors. Thus, the factors of 63 are 1, 3, 7, 9, 21 and 63.
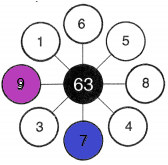
Therefore, 7 and 9 are the two factors that gives the 63.
Question 3.
![]()
Answer:
The square root of a number is defined as the value, which gives the number when it is multiplied by itself. The radical symbol √ is used to indicate the square root. For example, √9 = 3. The radical symbol is also called a root symbol or surds. If a number is a perfect square, we can easily find the square root of the number. If the given number is not a perfect square number, the square root can be found using the long division method.
– Here we will show you how to calculate the square root of 827 using the long division method with one decimal place accuracy.
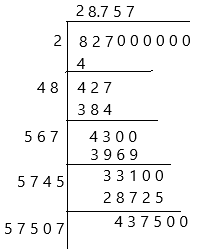
The answer is on top. The square root of 827 with one digit decimal accuracy is 28.757. Did you notice that the last two steps repeat the previous two steps? You can add decimals by simply adding more sets of 00 and repeating the last two steps over and over.
therefore, the square root of 827 is 28.757
The above-given question is 6 square root of 28.757 is:
We got a square root of 827 is 28.757
Now multiply 6 by 28.757
Thus, 6*28.757 is 172.542.
Question 4.
Which digit is in the thousand’s place in the number 45,678?
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The above-given number is 45,678.
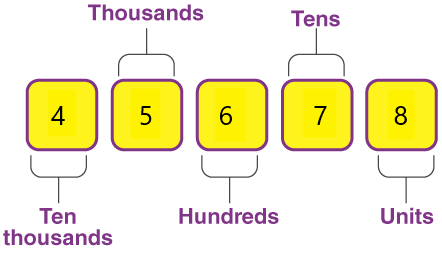
The 5 is in the thousands place.
Question 5.
Write 0.25 as a fraction.
Answer:
To write 0.25 as a fraction you have to write 0.25 as the numerator and put 1 as the denominator. Now you multiply the numerator and denominator by 10 as long as you get in the numerator the whole number.
0.25 = 0.25/1 = 2.5/10 = 25/100
And finally, we have:
0.25 as a fraction equals 25/100.
Question 6.
15 × 3 + 25 = __________
Answer:
The value of 15 × 3 is 45
Now add 45 to 25 then we get the answer. Assume that the answer is X.
X = 45 + 25
X = 70
Therefore, the answer for the above-given equation is 70.
Question 7.
![]() × 8 = 168
× 8 = 168
Answer:
Let the empty box be S
S × 8 = 168
Now get 8 into the right-hand side then the equation will be:
S = 168/8
S = 21
Now verify the answer by putting the S value in the above-given equation.
S × 8 = 168
21 × 8 = 168
168 = 168
Left-hand side = right-hand side
Hence, the answer is verified.
Question 8.
Calculate the perimeter of a rectangle that is 7 cm by 3 cm.
Answer:
A rectangle is a four-sided polygon. All of its angles are right angles (90°) and its opposite parallel sides are always of equal length. The perimeter of a rectangle is the total length of its figure, known as the sum of the length of all the sides of the rectangle. Meaning that you have to add the lengths of its sides to find its perimeter.
The formula for perimeter:
To calculate the perimeter, you simply have to add up the side lengths of the rectangle. Since the parallel sides of a rectangle are always equal, you only need to find the length of two sides in order to find the perimeter of the rectangle.
If we suppose a rectangle has length as a and width as b. The formula for the perimeter P is:
P = a+a+b+b
P = 2a+2b
P = 2(a+b)
Hence, the formula for the perimeter of a rectangle is 2 x (sum of adjacent sides)
Given: The length and width of the rectangle are 7 cm and 3 cm, respectively
The perimeter of this rectangle is P = 2x(7+3)=20 cm.
Question 9.
How many angles are inside a quadrilateral?
Answer:
There are four interior angles in a quadrilateral and they add up to a sum of 360°. This value is obtained using the angle sum property of a quadrilateral.
Interior angles of a quadrilateral:
The angles that lie inside a quadrilateral are called its interior angles. The sum of the interior angles of a quadrilateral is 360°. This helps in calculating the unknown angles of a quadrilateral. In case the quadrilateral is a square or a rectangle, then we know that all its interior angles are 90° each.
Question 10.
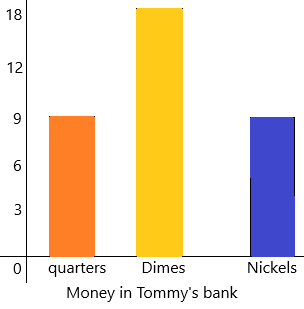
Create a bar graph based on the tally chart below. Label the graph.
Money in Tommy’s Bank
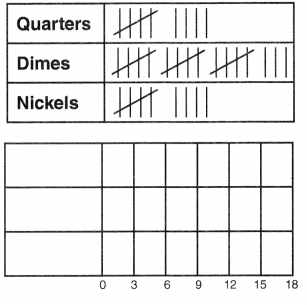
Answer:
The pictorial representation of grouped data, in the form of vertical or horizontal rectangular bars, where the lengths of the bars are equivalent to the measure of data, are known as bar graphs or bar charts.
Properties of a bar graph:
Some of the important properties of a bar graph are as follows:
– All the bars should have a common base.
– Each column in the bar graph should have equal width.
– The height of the bar should correspond to the data value.
– The distance between each bar should be the same.
Question 11.
A family has five members: a mom, a dad, two sisters, and a brother. The family lines up a single file. What is the probability that the grandma is at the front of the line?
Answer:
This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes)
P(A) = n(E) / n(S)
P(A) < 1
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event.
The total number of possible outcomes = 5
The number of favourable outcomes = 1
P(grand maa) = 1/5
Well, the probability that the grandma in front of the line is 1/5.
Question 12.
Raj has a collection of 30 toy cars. One-third of his collection is trucks. One-half of the collection ¡s racing cars. The rest are sports cars. How many sports cars are in his collection?
Answer:
The total collection of toys = 30
The collection of toy cars in trucks = 1/3rd
1/3rd of toys = 1/3 * 30 = 10|
The number of toys in trucks = 10
Now remaining cars =30-10 = 20
The collection of toy cars in racing cars = 1/2
1/2 of toys = 1/2 * 20 = 10
The number of toys in racing cars = 10
and within 30 cars, 10 of them are in trucks and 10 of them are in racing cars; and the remaining cars are in sports cars.
Now total of 30 toy cars.